The optical Bloch equations
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604d2158dbbebf16674738f973827dbb18e3a819)
provide a time-dependent quantum
description of a spontaneously emitting atom driven by a classical
electromagnetic field. Considerable insight into the physical
processes involved can be gained by studying these equations in the
transient excitation limit, as well as the steady-state limit, as we
see in this section. We begin by considering the coherent part of the
evolution, then extend this to re-visit the Bloch sphere picture of
the optical Bloch equations, which provides useful visualizations of
transient responses and steady state solutions. Finally, we return to vacuum Rabi oscillations and investigate how cavity loss leads to damping of the oscillations, as an illustration of master equations which are more general than the optical Bloch equation.
Eigenstates of the Jaynes-Cummings Hamiltonian
The Hamiltonian involved in the optical Bloch equations,

describes the evolution of an atom in a classical field.
We begin here by reviewing the coherent
evolution under  .
.
 arises from the Jaynes-Cummings interaction we have previously
considered in the context of cavity QED, describing a single two-level
atom interacting with a single mode of the electromagnetic field:
arises from the Jaynes-Cummings interaction we have previously
considered in the context of cavity QED, describing a single two-level
atom interacting with a single mode of the electromagnetic field:
![{\displaystyle H_{JC}={\frac {\hbar \omega _{0}}{2}}\left[{|e\rangle \langle e|-|g\rangle \langle g|}\right]+\hbar \omega a^{\dagger }a+{\frac {\hbar \Omega }{2}}\left[{|g\rangle \langle e|+|e\rangle \langle g|}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/630609e3aab033690555f530c6e4323ba84a5538)
The last term in this expression is  , the dipole interaction
between atom and field. By defining
, the dipole interaction
between atom and field. By defining  and
and
 , we may write this interaction as
, we may write this interaction as
![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{\sigma _{+}+\sigma _{-}}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3410ceeb8ffe707f367fc599209a8dad817b08df)
In the frame of reference of the atom and field, recall that

When near resonance,  , and because the
, and because the
 and
and  terms oscillate at nearly twice the frequency
of
terms oscillate at nearly twice the frequency
of  , those terms can be dropped. Doing so is known as the
rotating wave approximation, and it gives us a simplified
interaction Hamiltonian
, those terms can be dropped. Doing so is known as the
rotating wave approximation, and it gives us a simplified
interaction Hamiltonian
![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{a^{\dagger }\sigma _{-}+a\sigma _{+}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60d32887d250fa22239d00c10278b510514772e)
Under this approximation, it is useful to note that this interaction
merely exchanges one quantum of excitation from atom to field, and
back, so that the total number of excitations  is a constant of the motion. We may thus write the total Hamiltonian,
in the rotating frame with the rotating wave approximation, as
is a constant of the motion. We may thus write the total Hamiltonian,
in the rotating frame with the rotating wave approximation, as

where we have defined  , and
, and  . Below, we may use
. Below, we may use  to simplify
writing.
to simplify
writing.
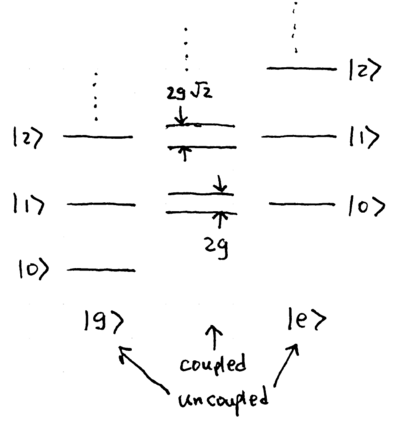
What are the eigenstates of this Hamiltonian? It describes a
two-level system coupled to a simple harmonic oscillator; when
uncoupled, if  , then the eigenstates are simply those of
, then the eigenstates are simply those of
 ,
,  and
and  , as shown here:
, as shown here:
When coupled, degenerate energy levels split (this is sometimes called dynamimc Stark splitting), with harmonic oscillator
levels  and
and  splitting into two energy levels separated
by
splitting into two energy levels separated
by  . Since the coupling only pairs levels separated by
one quantum of excitation, it is straightforward to show that the
eigenstates of the Jaynes-Cummings Hamiltonian fall into well defined
pairs of states, which we may label as
. Since the coupling only pairs levels separated by
one quantum of excitation, it is straightforward to show that the
eigenstates of the Jaynes-Cummings Hamiltonian fall into well defined
pairs of states, which we may label as  ; these are
; these are
![{\displaystyle |\pm ,n\rangle ={\frac {1}{\sqrt {2}}}\left[{|e,n\rangle \pm |g,n+1\rangle }\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55f08b48a6a98c378c7ba35aff03487dd1c3463e)
and they have energies

When  , similar physics result, but with slightly more
complicated expressions describing the eigenstates, as we shall see
when we later return to the "dressed states" picture.
, similar physics result, but with slightly more
complicated expressions describing the eigenstates, as we shall see
when we later return to the "dressed states" picture.
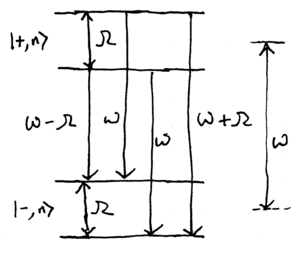
Strongly driven atom: Mollow triplet
An atom strongly coupled to a single mode electromagnetic field, or an
atom driven strongly by a single mode field, will thus have an
emission spectrum described by the coupled energy level diagram:
where, to good approximation, the energy level differences are
 and
and  . These three lines which appear in the
spectrum are known as the Mollow triplet:
. These three lines which appear in the
spectrum are known as the Mollow triplet:
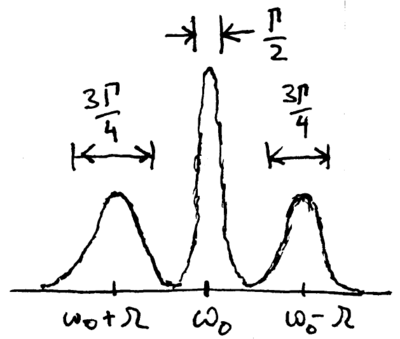
The Mollow triplet is experimentally observed in a wide variety of
systems. However, while our energy eigenstate analysis has predicted
the number and frequencies of the emission lines, it fails to explain
a key characteristic: the widths are not the same. If the central
peak at  has width HWHM
has width HWHM  , the two sidebands each have a
HWHM of
, the two sidebands each have a
HWHM of  . To explain this, we need the optical Bloch
equations.
. To explain this, we need the optical Bloch
equations.
Optical Bloch equation evolution on the Bloch sphere
We have previously seen that an arbitrary qubit state  can be represented as being a
point on a unit sphere, located at
can be represented as being a
point on a unit sphere, located at  in polar
coordinates. Similarly, a density matrix
in polar
coordinates. Similarly, a density matrix  may be depicted as
being a point inside or on the unit sphere, using
may be depicted as
being a point inside or on the unit sphere, using

where  is the Bloch vector representation of
is the Bloch vector representation of  .
.
Explicitly, if we let
- Failed to parse (syntax error): {\displaystyle |0{\rangle}=|e{\rangle} = \left[ \begin{array}{cc}{1}\\{0}\end{array}\right], |1{\rangle}=|g{\rangle} = \left[ \begin{array}{cc}{0}\\{1}\end{array}\right], \\ \rho = \left[ \begin{array}{cc}{\rho_{ee}}&{\rho_{eg}}\\{\rho_{ge}}&{\rho_{gg}}\end{array}\right] \,, }
then

Which can be reversed to find

Visualization: Bloch vector
Visulization of the evolution of a density matrix under the optical
Bloch equations is thus helped by rewriting them in terms of a
differential equation for  . A convenient starting point for
this is the optical Bloch equation
. A convenient starting point for
this is the optical Bloch equation
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604d2158dbbebf16674738f973827dbb18e3a819)
using the rotating frame Hamiltonian derived in AMO I Resonances
![{\displaystyle H={\frac {\hbar }{2}}\left(-\delta Z+\Omega X\right)={\frac {\hbar }{2}}\left[{\begin{array}{cc}{-\delta }&{\Omega }\\{\Omega }&{\delta }\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/492a8aba8b716785e12c716ce476c423a1444b73)
This gives us the equations of motion

Note how these equations of motion provide a simple set of flows on
the Bloch sphere: the  terms correspond to a rotation in the
terms correspond to a rotation in the
 plane,
plane,  corresponds to a rotation in the
corresponds to a rotation in the
 plane, and
plane, and  drives a relaxation process
which shrinks
drives a relaxation process
which shrinks  and
and  components of the Bloch vector,
while moving the
components of the Bloch vector,
while moving the  component toward
component toward  .
.
Physics: in-phase and quadrature components
Physically, what is the meaning of  ,
,  , and
, and  ?
?  is
manifestly the population difference between the excited and ground
states. The other two components may be interpreted by recognizing
that the average dipole moment of the atom is
is
manifestly the population difference between the excited and ground
states. The other two components may be interpreted by recognizing
that the average dipole moment of the atom is

Thus,  and
and  correspond to the phase components of the atomic
dipole moment which are in-phase and in quadrature with the incident
electromagnetic field.
correspond to the phase components of the atomic
dipole moment which are in-phase and in quadrature with the incident
electromagnetic field.
Animation of full solutions
Here are plots of the full solutions of the optical Bloch equations on the Bloch sphere, for various cases of  ,
,  , and
, and  (sample matlab files to solve the differential equations: obefun1.m
plotobe2.m):
(sample matlab files to solve the differential equations: obefun1.m
plotobe2.m):
<jwplayer width="560" height="440" repeat="true" displayheight="420"
image="http://feynman.mit.edu/8.422/plotobe6.png"
autostart="false">http://feynman.mit.edu/8.422/plotobe6.flv</jwplayer>
Solutions of the optical Bloch equations
The optical Bloch equations, describing the evolution of a single atom coupled to the vacuum,
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604d2158dbbebf16674738f973827dbb18e3a819)
are a set of three coupled differential equations,

written in the rotating frame of the atom's Hamiltonian. These equations can be solved analytically, but a great deal of intuition can be obtained from just studying the solutions in several limits. Here, we consider the steady state, transient, and weak excitation limits.
Transient response of the optical Bloch equations
The optical Bloch equations allow us to study the internal state of
the atom as it changes due to the external driving field, and due to
spontaneous emission.
Starting from the time-independent form of the equations,

we may note that when  and at resonance,
and at resonance,  ,
the Bloch vector exhibits pure damping behavior, towards
,
the Bloch vector exhibits pure damping behavior, towards  , and
, and
 . Note that a convenient way to write these differential equations is in matrix form,
. Note that a convenient way to write these differential equations is in matrix form,
![{\displaystyle {\dot {\vec {r}}}=\left[{\begin{array}{ccc}{-\Gamma /2}&{\delta }&{0}\\{-\delta }&-\Gamma /2&-\Omega \\0&\Omega &-\Gamma \end{array}}\right]{\vec {r}}+\left[{\begin{array}{c}0\\0\\-\Gamma \end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a580cad68617ecfb286f1dd0bf82375e72f0868f)
When  , Rabi oscillations occur, represnted by rapid
rotations of the Bloch vector about
, Rabi oscillations occur, represnted by rapid
rotations of the Bloch vector about  . Since the relaxation
along
. Since the relaxation
along  occurs at rate
occurs at rate  , and the relaxation about
, and the relaxation about
 occurs at rate
occurs at rate  , we might expect that the average
relaxation rate of the rotating components under such a strong driving
field would be
, we might expect that the average
relaxation rate of the rotating components under such a strong driving
field would be  . The remaining
component
. The remaining
component  does not rotate, because it sits along
does not rotate, because it sits along  , the
axis of rotation. Thus, it relaxes with rate
, the
axis of rotation. Thus, it relaxes with rate  . Computation of the eigenvalues of the equations of motion verify this qualitative
picture, and show that for
. Computation of the eigenvalues of the equations of motion verify this qualitative
picture, and show that for  , and
, and  , the
eigenvalues of motion are
, the
eigenvalues of motion are  and
and  .
.
These
correspond to a main peak at  with width
with width  , and two
sidebands at
, and two
sidebands at  , with widths
, with widths  , thus
explaining the widths of the observed Mollow triplet lines.
, thus
explaining the widths of the observed Mollow triplet lines.
Steady-state solution of the optical Bloch equations
The steady state solution of the optical Bloch equations are found by
setting all the time derivatives to zero, giving a set of three
simultaneous equations,
Starting from the time-independent form of the equations,

The solutions are:

Physically, these are Lorentzians; the  solution (the component
in quadrature with the dipole) corresponds to an absorption curve with
half-width
solution (the component
in quadrature with the dipole) corresponds to an absorption curve with
half-width

and the  solution (the component in-phase with the dipole)
corresponds to a dispersion curve. And under a strong driving field,
as
solution (the component in-phase with the dipole)
corresponds to a dispersion curve. And under a strong driving field,
as  ,
,  , indicating that the
populations in the excited and ground states are equalizing. The
steady-state population in the excited state is
, indicating that the
populations in the excited and ground states are equalizing. The
steady-state population in the excited state is

an important result that will later be used in studying light forces.
These solutions can be re-expressed in a simplified manner by defining
the saturation parameter

in terms of which we find

As  , the atomic transitions become saturated, and the linewidth of the transition broadens from its
natural value
, the atomic transitions become saturated, and the linewidth of the transition broadens from its
natural value  , becoming
, becoming  on
resonance, at
on
resonance, at  .
.
Here are plots of the steady state solution for varying  :
:
<jwplayer width="560" height="440" repeat="true" displayheight="420"
image="http://feynman.mit.edu/8.422/steady4.png"
autostart="false">http://feynman.mit.edu/8.422/steady4.flv</jwplayer>
Weak excitation limit solution of the optical Bloch equations
Once again, the time-independent form of the optical Bloch equations is

where the remaining two components of the density matrix are given by
 , and
, and  . It is
insightful to study these equations in the limit of weak excitation,
and for short evolution times.
. It is
insightful to study these equations in the limit of weak excitation,
and for short evolution times.
It turns out that the solution of these equations to lowest order
in  , and in the limit
, and in the limit  , with the initial
conditions
, with the initial
conditions  and
and  , gives
, gives
![{\displaystyle \rho _{ee}={\frac {{\frac {1}{4}}|\Omega |^{2}}{\delta ^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}\left[{1+e^{-\Gamma t}-2\cos(\delta t)e^{-\Gamma t/2}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c19bf5cb1660757c54d1ccc65a9f0c4cbfcd57fe)
Moreover the solution of these equations to lowest order in
 in the limit
in the limit  , with the initial conditions
, with the initial conditions  and
and  , gives
, gives

irrespective of the values of  and
and  .
.
Damped vacuum Rabi oscillations
The optical Bloch equations can be generalized to describe not just an
atom interacting with the vacuum, but also an atom and a single cavity
mode, each interacting with its own reservoir. This is the master
equation for cavity QED, and using such a master equation we can
revisit the phenomenon of vacuum Rabi oscillations and see what
happens in the presence of damping.
Generalization of the optical Bloch equations
The starting point for generalizing the optical Bloch equations is the
Lindblad form we previously saw in the
full-derivation walkthrough,
![{\displaystyle {\dot {\rho }}_{A}=-{\frac {i}{\hbar }}[H,\rho _{A}]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho _{A}-2\sigma _{-}\rho _{A}\sigma _{+}+\rho _{A}\sigma _{+}\sigma _{-}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13bf26eb3d88c4444078e147d8e6751295dea1fd)
In this expression,  and
and  are "jump operators,"
and represent changes that occur to the atom when distinct dissipative
events happen ("distinct" meaning that the environment changes
between orthogonal states).
are "jump operators,"
and represent changes that occur to the atom when distinct dissipative
events happen ("distinct" meaning that the environment changes
between orthogonal states).
We may write the master equation for our more general scenario by
replacing the atomic density matrix  by a general density
matrix
by a general density
matrix  representing the atom and cavity field, and by replacing
the atomic jump operators with general jump operators
representing the atom and cavity field, and by replacing
the atomic jump operators with general jump operators  ,
,
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]+\sum _{k}\left[{L_{k}\rho L_{k}^{\dagger }-{\frac {1}{2}}(L_{k}^{\dagger }L_{k}\rho +\rho L_{k}^{\dagger }L_{k})}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f41a3c9853e8923bf9cfd246f4affa45f6e6039a)
Note that the  include normalization factors which reflect their
probabilities of occurrence. In other words, for the atom + vacuum
model,
include normalization factors which reflect their
probabilities of occurrence. In other words, for the atom + vacuum
model,  .
.
Master equation for cavity QED system
For the cavity QED model, the atom and cavity field each have possible
jump operators. In general, the atom and cavity may both couple to a
thermal field with  average photons. In such a case, the jump
operators are
average photons. In such a case, the jump
operators are  ,
,  ,
,  , and
, and
 , where
, where  parameterizes the
spontaneous emission rate of the atom in free space, and
parameterizes the
spontaneous emission rate of the atom in free space, and  is
parameterizes the cavity
is
parameterizes the cavity  factor.
factor.
Experimentally, typically the
environment, the vacuum, is essentially at zero temperature, so
 , in which case the only two relevant jump operators are
, in which case the only two relevant jump operators are
 and
and  .
.
Damped vacuum Rabi oscillations
Vacuum Rabi oscillations, in the absence of damping, involve only two
states of the atom and cavity:  and
and  . When damping is
added, the
. When damping is
added, the  state must be included, since both the atom and
cavity states can decay and loose their quanta of energy. Moreover,
because only one quantum of excitation is involved in this system, we
can observe the essential physics by considering the case when
state must be included, since both the atom and
cavity states can decay and loose their quanta of energy. Moreover,
because only one quantum of excitation is involved in this system, we
can observe the essential physics by considering the case when
 is zero (no spontaneous emission), but
is zero (no spontaneous emission), but  is nonzero
(the cavity is leaky). Let
is nonzero
(the cavity is leaky). Let  be the vacuum Rabi frequency,
and denote this three state space by
be the vacuum Rabi frequency,
and denote this three state space by  ,
,  , and
, and
 . Written out explicitly in terms of the
. Written out explicitly in terms of the  density matrix elements
density matrix elements  , the master equation is (for the case
, the master equation is (for the case  with the system starting in the state
with the system starting in the state  )
)

When the cavity damping rate is small,  , then the
vacuum Rabi oscillations are damped, with average damping rate
, then the
vacuum Rabi oscillations are damped, with average damping rate
 since the atoms spend roughly half their time in the excited state.
since the atoms spend roughly half their time in the excited state.
When the cavity damping rate is large,  , then the
atomic excitation is irreversibly damped, and no oscillations occur.
Let
, then the
atomic excitation is irreversibly damped, and no oscillations occur.
Let  be the probability of being in the
be the probability of being in the  state. We can combine two of the above equations to write
state. We can combine two of the above equations to write

Since in this case  , and
, and
 , it follows that
, it follows that

Since in this regime, we slowly try to populate state  while it quickly decays away, we can approximate
while it quickly decays away, we can approximate  giving
giving

Finally plugging this back into the optical bloch equation for  yields
yields

so  decays exponentially, with rate
decays exponentially, with rate  .
Note that a large cavity damping rate slows down the decay of the atom's excited state. This is due to the fact that the stimulated transition (Rabi oscillation) to the lower state is slowed down by the cavity damping (which is a manifestation of the quantum Zeno effect).
.
Note that a large cavity damping rate slows down the decay of the atom's excited state. This is due to the fact that the stimulated transition (Rabi oscillation) to the lower state is slowed down by the cavity damping (which is a manifestation of the quantum Zeno effect).
Purcell factor: cavity enhanced spontaneous emission
How does this compare with the free space spontaneous emission rate
 ? Recall that the vacuum Rabi frequency is (for the case that the dipole matrix element vector and cavity mode polarization are aligned)
? Recall that the vacuum Rabi frequency is (for the case that the dipole matrix element vector and cavity mode polarization are aligned)

where  is the atomic dipole moment and
is the atomic dipole moment and  is the electric field
amplitude of a single photon at the atomic transition frequency
is the electric field
amplitude of a single photon at the atomic transition frequency
 (Note that this is a standing wave in a cavity so it is a factor of two larger than the field for a running wave),
(Note that this is a standing wave in a cavity so it is a factor of two larger than the field for a running wave),

and  is the cavity volume. This gives
is the cavity volume. This gives

Letting  , we thus find that
, we thus find that

as the decay rate of the atom in the cavity.
Recall that the spontaneous emission rate of an atom in free space, as
determined by Fermi's golden rule, is

The ratio of this rate to the decay rate in the cavity is

where we take  as being the wavelength of
the cavity field, which is assumed to be resonant with the atomic
transition frequency
as being the wavelength of
the cavity field, which is assumed to be resonant with the atomic
transition frequency  . Note that
. Note that  is independent of the atomic dipole strength, and determined solely by
cavity parameters. Moreover, note that for small, high-
is independent of the atomic dipole strength, and determined solely by
cavity parameters. Moreover, note that for small, high- cavities, the decay rate of the atom in the
cavity can be much larger than the free space spontaneous emission
rate. This "cavity enhanced" spontaneous emission rate was predicted
by Purcell (1946), an observation credited as being the starting point
of cavity QED.
cavities, the decay rate of the atom in the
cavity can be much larger than the free space spontaneous emission
rate. This "cavity enhanced" spontaneous emission rate was predicted
by Purcell (1946), an observation credited as being the starting point
of cavity QED.
References
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604d2158dbbebf16674738f973827dbb18e3a819)


![{\displaystyle H_{JC}={\frac {\hbar \omega _{0}}{2}}\left[{|e\rangle \langle e|-|g\rangle \langle g|}\right]+\hbar \omega a^{\dagger }a+{\frac {\hbar \Omega }{2}}\left[{|g\rangle \langle e|+|e\rangle \langle g|}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/630609e3aab033690555f530c6e4323ba84a5538)



![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{\sigma _{+}+\sigma _{-}}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3410ceeb8ffe707f367fc599209a8dad817b08df)





![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{a^{\dagger }\sigma _{-}+a\sigma _{+}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60d32887d250fa22239d00c10278b510514772e)












![{\displaystyle |\pm ,n\rangle ={\frac {1}{\sqrt {2}}}\left[{|e,n\rangle \pm |g,n+1\rangle }\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55f08b48a6a98c378c7ba35aff03487dd1c3463e)













![{\displaystyle H={\frac {\hbar }{2}}\left(-\delta Z+\Omega X\right)={\frac {\hbar }{2}}\left[{\begin{array}{cc}{-\delta }&{\Omega }\\{\Omega }&{\delta }\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/492a8aba8b716785e12c716ce476c423a1444b73)


















![{\displaystyle {\dot {\vec {r}}}=\left[{\begin{array}{ccc}{-\Gamma /2}&{\delta }&{0}\\{-\delta }&-\Gamma /2&-\Omega \\0&\Omega &-\Gamma \end{array}}\right]{\vec {r}}+\left[{\begin{array}{c}0\\0\\-\Gamma \end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a580cad68617ecfb286f1dd0bf82375e72f0868f)























![{\displaystyle \rho _{ee}={\frac {{\frac {1}{4}}|\Omega |^{2}}{\delta ^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}\left[{1+e^{-\Gamma t}-2\cos(\delta t)e^{-\Gamma t/2}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c19bf5cb1660757c54d1ccc65a9f0c4cbfcd57fe)



![{\displaystyle {\dot {\rho }}_{A}=-{\frac {i}{\hbar }}[H,\rho _{A}]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho _{A}-2\sigma _{-}\rho _{A}\sigma _{+}+\rho _{A}\sigma _{+}\sigma _{-}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13bf26eb3d88c4444078e147d8e6751295dea1fd)




![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]+\sum _{k}\left[{L_{k}\rho L_{k}^{\dagger }-{\frac {1}{2}}(L_{k}^{\dagger }L_{k}\rho +\rho L_{k}^{\dagger }L_{k})}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f41a3c9853e8923bf9cfd246f4affa45f6e6039a)
















































