Saturation
The saturated transition rate
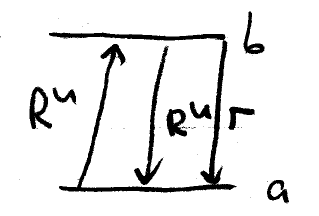
Consider an ensemble of  two-lvel atoms with levels
two-lvel atoms with levels  and
and
 :
:
 is the spontaneous emission rate, and
is the spontaneous emission rate, and  is the transition
rate given by the coupling between incident photons and the atoms. We
call
is the transition
rate given by the coupling between incident photons and the atoms. We
call  the unsaturated transition rate, because the actual
net transfer rate from
the unsaturated transition rate, because the actual
net transfer rate from  to
to  , is close to
, is close to  only when
most atoms start in state
only when
most atoms start in state  . When a sizable fraction of the
. When a sizable fraction of the  atoms are already excited, the net transfer rate slows down.
Eventually, upon sufficient excitation, the number of atoms in the two
states,
atoms are already excited, the net transfer rate slows down.
Eventually, upon sufficient excitation, the number of atoms in the two
states,  and
and  no longer change. Between these two extremes,
it is useful to define a saturated transition rate
no longer change. Between these two extremes,
it is useful to define a saturated transition rate  , which
gives the net transfer rate from
, which
gives the net transfer rate from  to
to  caused by incident
photons, per atom in the ensemble. What is a mathematical expression
for
caused by incident
photons, per atom in the ensemble. What is a mathematical expression
for  ?
The rate equations governing the atomic populations are:
?
The rate equations governing the atomic populations are:

In the absence of spontaneous emission, these eqautions show that the
net transition rate between the levels is given by  , so
that the saturated transition rate is
, so
that the saturated transition rate is

The steady state populations, obtained by setting  and
and
 to zero, satisfy
to zero, satisfy

which can be conveneintly re-expressed as

by defining the saturation parameter

We will return later to the physical meaning of the saturation parameter.
Subsituting this into the definition of  gives
gives

This is a very useful expression. In the limit of  (small
(small  ), far from saturation,
), far from saturation,  , and in the
limit of
, and in the
limit of  (
( ), complete saturation,
), complete saturation,
 .
.
Monochromatic Radiation
An important case is when the incident radiation is monochromatic, and
has a Lorentzian frequency distribution,  , where
, where  is the detuning from resonance. Recall that the unsaturated
transition rate is then given by
is the detuning from resonance. Recall that the unsaturated
transition rate is then given by

where  is the Rabi frequency. Substituting for
is the Rabi frequency. Substituting for  a normalized Lorentzian distribution,
a normalized Lorentzian distribution,

we obtain

and this expression for the saturation parameter

The saturated transition rate per atom, as a function of detuning, is thus

This is an important and useful expression. It tells us what the
transition rate is, as measured in an experiment, for example, by
absorption. Note that this is a Lorentzian distribution, with a width
which depends on  .
Defining the on-resonance saturation parameter
.
Defining the on-resonance saturation parameter

such that the saturation parameter is  , we find that the full width at half
maximum of
, we find that the full width at half
maximum of  is given by
is given by

indicating that the transition broadens in frequency as the
incident intensity of light (which determines  ) increases.
Physically, this happens because of the effective shortening of the
lifetime of atoms in
) increases.
Physically, this happens because of the effective shortening of the
lifetime of atoms in  due to the stimulated emission.
The saturated transition rate per atom, expressed in terms of
due to the stimulated emission.
The saturated transition rate per atom, expressed in terms of  , is
, is

and can be re-expressed using the power broadened linewidth  as
as

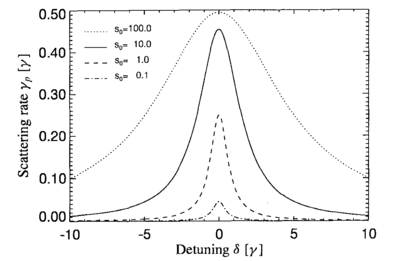
Note that in the limit that  ,
,  . A plot of this is shown below (figure from page 26 of {\em
Laser Cooling and Trapping}, by Metcalf and van der Straten;
. A plot of this is shown below (figure from page 26 of {\em
Laser Cooling and Trapping}, by Metcalf and van der Straten;  ):
):
Note that the transition rate from  to
to  , given in terms of
the absorption crosssection
, given in terms of
the absorption crosssection  , and the incident
intensity
, and the incident
intensity  , is
, is

where we may identify as the saturated absorption crossection

As  ,
,  . This
process is known as bleaching.
. This
process is known as bleaching.
Saturation Intensity
The on-resonance saturation parameter has a useful physical meaning.
At  , the unsaturated transition rate becomes
, the unsaturated transition rate becomes

were we have identified as the sauration intensity

This is a very useful quantity in practice. For the sodium D line,
 mW/cm
mW/cm , and that value is typical of most widely
used atomic transitions. In terms of
, and that value is typical of most widely
used atomic transitions. In terms of  , we may give
, we may give

This extrodinary  mW/cm
mW/cm value of
value of  can be
apprreciated by comparing the monochromatic excitation case, which we
have just analyzed, with the case of broadband excitation. For
broadband excitation,
can be
apprreciated by comparing the monochromatic excitation case, which we
have just analyzed, with the case of broadband excitation. For
broadband excitation,

where the approximation is valid in the limit that the average
intensity over the spectral density  (a useful approximation which gives a result
independent of the details of the transition). Here,
(a useful approximation which gives a result
independent of the details of the transition). Here,

which, for visible frequencies, is approximately  W/cm
W/cm per
inverse centimeter of bandwidth.
per
inverse centimeter of bandwidth.