Difference between revisions of "Solutions of the optical Bloch equations"
imported>Ichuang |
imported>Zakven |
||
| (58 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The optical Bloch equations provide a time-dependent quantum | + | The optical Bloch equations |
| + | :<math> | ||
| + | \dot{\rho} = -\frac{i}{\hbar}[H,\rho] | ||
| + | -\frac{\Gamma}{2} \left[ { \sigma_+ \sigma_- \rho - 2 \sigma_- \rho \sigma_+ | ||
| + | + \rho \sigma_+ \sigma_- } \right] | ||
| + | \,, | ||
| + | </math> | ||
| + | provide a time-dependent quantum | ||
description of a spontaneously emitting atom driven by a classical | description of a spontaneously emitting atom driven by a classical | ||
electromagnetic field. Considerable insight into the physical | electromagnetic field. Considerable insight into the physical | ||
| Line 7: | Line 14: | ||
evolution, then extend this to re-visit the Bloch sphere picture of | evolution, then extend this to re-visit the Bloch sphere picture of | ||
the optical Bloch equations, which provides useful visualizations of | the optical Bloch equations, which provides useful visualizations of | ||
| − | transient responses and steady state solutions. | + | transient responses and steady state solutions. Finally, we return to [[Atoms_and_cavities#Vacuum_Rabi_Oscillations|vacuum Rabi oscillations]] and investigate how cavity loss leads to damping of the oscillations, as an illustration of master equations which are more general than the optical Bloch equation. |
<categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;" hideprefix=auto>8.422</categorytree> | <categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;" hideprefix=auto>8.422</categorytree> | ||
=== Eigenstates of the Jaynes-Cummings Hamiltonian === | === Eigenstates of the Jaynes-Cummings Hamiltonian === | ||
| − | The optical Bloch equations | + | |
| − | + | The Hamiltonian involved in the optical Bloch equations, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> | :<math> | ||
H = \frac{\hbar\omega_0}{2}(|e \rangle \langle e|-|g \rangle \langle g|) | H = \frac{\hbar\omega_0}{2}(|e \rangle \langle e|-|g \rangle \langle g|) | ||
+ \frac{\hbar\Omega}{2} (|g \rangle \langle e|+|e \rangle \langle g|) | + \frac{\hbar\Omega}{2} (|g \rangle \langle e|+|e \rangle \langle g|) | ||
| − | \, | + | \,, |
</math> | </math> | ||
| − | + | describes the evolution of an atom in a classical field. | |
| − | + | We begin here by reviewing the coherent | |
| − | |||
| − | |||
evolution under <math>H</math>. | evolution under <math>H</math>. | ||
| + | |||
<math>H</math> arises from the Jaynes-Cummings interaction we have previously | <math>H</math> arises from the Jaynes-Cummings interaction we have previously | ||
| − | considered in the context of cavity QED, describing a single two-level | + | considered in the context of [[Atoms and cavities|cavity QED]], describing a single two-level |
atom interacting with a single mode of the electromagnetic field: | atom interacting with a single mode of the electromagnetic field: | ||
:<math> | :<math> | ||
| Line 54: | Line 54: | ||
\\ \sigma_- a &\rightarrow& e^{-i(\omega+\omega_0)t} \sigma_- a | \\ \sigma_- a &\rightarrow& e^{-i(\omega+\omega_0)t} \sigma_- a | ||
\\ \sigma_+ a &\rightarrow& e^{i(\omega_0-\omega)t} \sigma_+ a | \\ \sigma_+ a &\rightarrow& e^{i(\omega_0-\omega)t} \sigma_+ a | ||
| − | \\ \sigma_- a^\dagger &\rightarrow& e^{-i(\omega_0-\ | + | \\ \sigma_- a^\dagger &\rightarrow& e^{-i(\omega_0-\omega)t} \sigma_- a^\dagger |
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| Line 61: | Line 61: | ||
of <math>\omega</math>, those terms can be dropped. Doing so is known as the | of <math>\omega</math>, those terms can be dropped. Doing so is known as the | ||
rotating wave approximation, and it gives us a simplified | rotating wave approximation, and it gives us a simplified | ||
| − | + | interaction Hamiltonian | |
:<math> | :<math> | ||
H_I = \frac{\hbar\Omega}{2} | H_I = \frac{\hbar\Omega}{2} | ||
| − | \left[ { a^\dagger \sigma_ | + | \left[ { a^\dagger \sigma_- + a \sigma_+ } \right] |
\,. | \,. | ||
</math> | </math> | ||
| Line 71: | Line 71: | ||
back, so that the total number of excitations <math>N= a^\dagger a + |e \rangle \langle e|</math> | back, so that the total number of excitations <math>N= a^\dagger a + |e \rangle \langle e|</math> | ||
is a constant of the motion. We may thus write the total Hamiltonian, | is a constant of the motion. We may thus write the total Hamiltonian, | ||
| − | in the rotating wave approximation, as | + | in the rotating frame with the rotating wave approximation, as |
:<math> | :<math> | ||
| − | H = \hbar\omega N | + | H = \hbar\omega N - \delta \sigma_z + |
\frac{\hbar\Omega}{2}( a^\dagger \sigma_- +a \sigma_+ ) | \frac{\hbar\Omega}{2}( a^\dagger \sigma_- +a \sigma_+ ) | ||
\,, | \,, | ||
</math> | </math> | ||
where we have defined <math>\sigma_z = |e \rangle \langle e|-|g \rangle \langle g|</math>, and <math>\delta = | where we have defined <math>\sigma_z = |e \rangle \langle e|-|g \rangle \langle g|</math>, and <math>\delta = | ||
| − | \ | + | \omega-\omega_0</math>. Below, we may use <math>g = \Omega/2</math> to simplify |
writing. | writing. | ||
| + | |||
What are the eigenstates of this Hamiltonian? It describes a | What are the eigenstates of this Hamiltonian? It describes a | ||
two-level system coupled to a simple harmonic oscillator; when | two-level system coupled to a simple harmonic oscillator; when | ||
| Line 85: | Line 86: | ||
<math>|e{\rangle}</math>, <math>|g{\rangle}</math> and <math>|n{\rangle}</math>, as shown here: | <math>|e{\rangle}</math>, <math>|g{\rangle}</math> and <math>|n{\rangle}</math>, as shown here: | ||
::[[Image:Transient_and_steady_state_solutions_of_the_optical_Bloch_equations-obe-Hjc.png|thumb|400px|none|]] | ::[[Image:Transient_and_steady_state_solutions_of_the_optical_Bloch_equations-obe-Hjc.png|thumb|400px|none|]] | ||
| − | + | ||
| − | When coupled, degenerate energy levels split, with harmonic oscillator | + | When coupled, degenerate energy levels split (this is sometimes called ''dynamimc Stark splitting''), with harmonic oscillator |
levels <math>|n{\rangle}</math> and <math>|n+1{\rangle}</math> splitting into two energy levels separated | levels <math>|n{\rangle}</math> and <math>|n+1{\rangle}</math> splitting into two energy levels separated | ||
by <math>2g\sqrt{n+1}</math>. Since the coupling only pairs levels separated by | by <math>2g\sqrt{n+1}</math>. Since the coupling only pairs levels separated by | ||
| Line 111: | Line 112: | ||
emission spectrum described by the coupled energy level diagram: | emission spectrum described by the coupled energy level diagram: | ||
::[[Image:Transient_and_steady_state_solutions_of_the_optical_Bloch_equations-obe-mollow-energy.png|thumb|306px|none|]] | ::[[Image:Transient_and_steady_state_solutions_of_the_optical_Bloch_equations-obe-mollow-energy.png|thumb|306px|none|]] | ||
| − | |||
where, to good approximation, the energy level differences are | where, to good approximation, the energy level differences are | ||
<math>\omega</math> and <math>\omega\pm\Omega</math>. These three lines which appear in the | <math>\omega</math> and <math>\omega\pm\Omega</math>. These three lines which appear in the | ||
spectrum are known as the Mollow triplet: | spectrum are known as the Mollow triplet: | ||
| − | ::[[Image:Transient_and_steady_state_solutions_of_the_optical_Bloch_equations-obe-mollow.png|thumb| | + | ::[[Image:Transient_and_steady_state_solutions_of_the_optical_Bloch_equations-obe-mollow.png|thumb|400px|none|]] |
| + | |||
The Mollow triplet is experimentally observed in a wide variety of | The Mollow triplet is experimentally observed in a wide variety of | ||
systems. However, while our energy eigenstate analysis has predicted | systems. However, while our energy eigenstate analysis has predicted | ||
the number and frequencies of the emission lines, it fails to explain | the number and frequencies of the emission lines, it fails to explain | ||
a key characteristic: the widths are not the same. If the central | a key characteristic: the widths are not the same. If the central | ||
| − | peak at <math>\omega_0</math> has width <math>\Gamma/2</math>, the two sidebands each have a | + | peak at <math>\omega_0</math> has width HWHM <math>\Gamma/2</math>, the two sidebands each have a |
| − | + | HWHM of <math>3\Gamma/4</math>. To explain this, we need the optical Bloch | |
equations. | equations. | ||
| − | === | + | |
| − | + | === Optical Bloch equation evolution on the Bloch sphere === | |
| − | + | ||
| − | + | Let's examine the case of a two-level atom with an excited state <math>|e\rangle</math> with linewdith <math>\Gamma</math> that | |
| − | + | can decay to the ground state <math>|g\rangle</math>. We'll use the following conventions | |
:<math> | :<math> | ||
| − | + | |0{\rangle}=|e{\rangle} = \left[ \begin{array}{cc}{1}\\{0}\end{array}\right], |1{\rangle}=|g{\rangle} = \left[ \begin{array}{cc}{0}\\{1}\end{array}\right], | |
| + | \rho = \left[ \begin{array}{cc}{\rho_{ee}}&{\rho_{eg}}\\{\rho_{ge}}&{\rho_{gg}}\end{array} \right] | ||
| + | \\ X = \left[ \begin{array}{cc}{0}&{1}\\{1}&{0}\end{array} \right] , Y = \left[ \begin{array}{cc}{0}&{-i}\\{i}&{0}\end{array} \right] , Z = \left[ \begin{array}{cc}{1}&{0}\\{0}&{-1}\end{array} \right], | ||
| + | \sigma_+ = \left[ \begin{array}{cc}{0}&{1}\\{0}&{0}\end{array} \right], \sigma_- = \left[ \begin{array}{cc}{0}&{0}\\{1}&{0}\end{array} \right] | ||
\,, | \,, | ||
</math> | </math> | ||
| − | + | Recall that the optical Bloch equation is | |
| − | |||
| − | |||
| − | |||
:<math> | :<math> | ||
| − | + | \dot{\rho} = -\frac{i}{\hbar}[H,\rho] | |
| − | + | -\frac{\Gamma}{2} \left[ { \sigma_+ \sigma_- \rho - 2 \sigma_- \rho \sigma_+ | |
| − | + | + \rho \sigma_+ \sigma_- } \right] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | - \frac{\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\,, | \,, | ||
| − | |||
</math> | </math> | ||
| − | + | and the rotating frame Hamiltonian (as derived in [[Resonances|AMO I Resonances]]) is | |
| − | |||
:<math> | :<math> | ||
| − | + | H = \frac{\hbar}{2}\left(-\delta Z + \Omega X \right) = \frac{\hbar}{2} \left[ \begin{array}{cc}{-\delta}&{\Omega}\\{\Omega}&{\delta}\end{array}\right] | |
| − | |||
\,. | \,. | ||
</math> | </math> | ||
| − | + | Substituting these matrices into the optical Bloch equation and evaluating the right had side gives us the equations of motion | |
| − | + | :<math>\begin{array}{rcl} | |
| − | + | \dot{\rho}_{ee} &=& i\frac{\Omega}{2}(\rho_{eg}-\rho_{ge}) - \Gamma\rho_{ee} | |
| − | :<math> | + | \\ \dot{\rho}_{eg} &=& i\delta\rho_{eg} + i\frac{\Omega}{2}(\rho_{ee}-\rho_{gg}) - \frac{\Gamma}{2} \rho_{eg} |
| − | \ | + | \\ \dot{\rho}_{ge} &=& -i\delta\rho_{ge} - i\frac{\Omega}{2}(\rho_{ee}-\rho_{gg}) - \frac{\Gamma}{2} \rho_{ge} |
| − | + | \\ \dot{\rho}_{gg} &=& -i\frac{\Omega}{2}(\rho_{eg}-\rho_{ge}) + \Gamma\rho_{ee} | |
| − | |||
| − | |||
| − | |||
| − | |||
\,. | \,. | ||
| − | </math> | + | \end{array}</math> |
| − | + | As a quick sanity check, we see that <math>\dot{\rho}_{ee}=-\dot{\rho}_{gg}</math> and <math>\dot{\rho}_{ge}=\dot{\rho}^*_{eg}</math> | |
| − | + | as you would expect from taking the time derivative of the normalization condition <math>\rho_{ee}=1-\rho_{gg}</math> and the hermicity | |
| − | <math>\ | + | requirement <math>\rho_{ge}=\rho^*_{eg}</math>. Furthermore <math>i(\rho_{eg}-\rho_{ge})=i(\rho_{eg}-\rho^*_{eg})</math> is purely |
| − | + | real, which means that the time derivatives of <math>\rho_{ee}</math> and <math>\rho_{gg}</math> are purely real, which in turn means | |
| − | the | + | that <math>\rho_{ee}</math> and <math>\rho_{gg}</math> stay purely real as the density matrix evolves. |
| − | + | ||
| − | + | === Visualization: Bloch vector === | |
| − | |||
| − | |||
| − | + | This seemingly complicated evolution of the density matrix is easier to understand when visualized on the Bloch sphere. | |
We have previously seen that an arbitrary qubit state <math>|\psi \rangle = | We have previously seen that an arbitrary qubit state <math>|\psi \rangle = | ||
| − | \cos\theta|0 \rangle + e^{i\phi}\sin\ | + | \cos\frac{\theta}{2}|0 \rangle + e^{i\phi}\sin\frac{\theta}{2}|1{\rangle}</math> can be represented as being a |
point on a unit sphere, located at <math>(\theta,\phi)</math> in polar | point on a unit sphere, located at <math>(\theta,\phi)</math> in polar | ||
coordinates. Similarly, a density matrix <math>\rho</math> may be depicted as | coordinates. Similarly, a density matrix <math>\rho</math> may be depicted as | ||
| Line 201: | Line 175: | ||
</math> | </math> | ||
where <math>\vec{r}</math> is the Bloch vector representation of <math>\rho</math>. | where <math>\vec{r}</math> is the Bloch vector representation of <math>\rho</math>. | ||
| − | + | Writing out both sides of that expression allows us to see how the Bloch vector components are related to the elements of the density matrix | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
| − | + | \rho_{ee} &=& \frac{1}{2}\left(1+r_z\right) | |
| − | + | \\ \rho_{eg} &=& \frac{1}{2}\left(r_x-ir_y\right) | |
| − | \\ | + | \\ \rho_{ge} &=& \frac{1}{2}\left(r_x+ir_y\right) |
| + | \\ \rho_{gg} &=& \frac{1}{2}\left(1-r_z\right) | ||
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| − | + | And these relations can easily be reversed to find | |
| − | + | :<math>\begin{array}{rcl} | |
| − | + | r_x &=& \langle X \rangle &=& \rho_{ge}+\rho_{eg} | |
| − | + | \\ r_y &=& \langle Y \rangle &=& (\rho_{ge}-\rho_{eg})/i | |
| − | + | \\ r_z &=& \langle Z \rangle &=& \rho_{ee}-\rho_{gg} | |
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\,. | \,. | ||
| − | </math> | + | \end{array}</math> |
| − | + | We can then use these relations to rewrite the above differential equations for the elements of the density matrix into differential equations for | |
| + | the components of the Bloch vector. This gives | ||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
\dot{r}_x &=& \delta\, r_y - \frac{\Gamma}{2} r_x | \dot{r}_x &=& \delta\, r_y - \frac{\Gamma}{2} r_x | ||
| − | \\ \dot{r}_y &=& -\delta\, r_x - | + | \\ \dot{r}_y &=& -\delta\, r_x - \Omega\, r_z - \frac{\Gamma}{2} r_y |
| − | \\ \dot{r}_z &=& | + | \\ \dot{r}_z &=& \Omega\, r_y - \Gamma (r_z +1) |
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
Note how these equations of motion provide a simple set of flows on | Note how these equations of motion provide a simple set of flows on | ||
the Bloch sphere: the <math>\delta</math> terms correspond to a rotation in the | the Bloch sphere: the <math>\delta</math> terms correspond to a rotation in the | ||
| − | <math>\hat{x}-\hat{y}</math> plane, <math> | + | <math>\hat{x}-\hat{y}</math> plane, <math>\Omega</math> corresponds to a rotation in the |
<math>\hat{y}-\hat{z}</math> plane, and <math>\Gamma</math> drives a relaxation process | <math>\hat{y}-\hat{z}</math> plane, and <math>\Gamma</math> drives a relaxation process | ||
which shrinks <math>\hat{x}</math> and <math>\hat{y}</math> components of the Bloch vector, | which shrinks <math>\hat{x}</math> and <math>\hat{y}</math> components of the Bloch vector, | ||
| − | while moving the <math>\hat{z}</math> component toward <math>r_z=1</math>. | + | while moving the <math>\hat{z}</math> component toward <math>r_z=-1</math>. |
| + | |||
| + | === Physics: in-phase and quadrature components === | ||
| + | |||
Physically, what is the meaning of <math>r_x</math>, <math>r_y</math>, and <math>r_z</math>? <math>r_z</math> is | Physically, what is the meaning of <math>r_x</math>, <math>r_y</math>, and <math>r_z</math>? <math>r_z</math> is | ||
manifestly the population difference between the excited and ground | manifestly the population difference between the excited and ground | ||
| Line 250: | Line 216: | ||
&=& d_{ge} (\rho_{ge} e^{i\omega t} + \rho_{eg} e^{-i\omega t}) | &=& d_{ge} (\rho_{ge} e^{i\omega t} + \rho_{eg} e^{-i\omega t}) | ||
\\ | \\ | ||
| − | &=& d_{ge} (r_x \cos\omega t | + | &=& d_{ge} (r_x \cos\omega t - r_y \sin\omega t) |
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| Line 257: | Line 223: | ||
electromagnetic field. | electromagnetic field. | ||
| − | === Transient | + | === Animation of full solutions === |
| + | |||
| + | Here are plots of the full solutions of the optical Bloch equations on the Bloch sphere, for various cases of <math>\Omega</math>, <math>\delta</math>, and <math>\Gamma</math> (sample matlab files to solve the differential equations: [http://cua.mit.edu/wikipost/20090304-131009/obefun1.m.txt obefun1.m] | ||
| + | [http://cua.mit.edu/wikipost/20090304-131009/plotobe2.m.txt plotobe2.m]). | ||
| + | In this video we have the ground state at the top of the Bloch sphere and the frequencies are given relative to <math>g=\Omega/2</math> | ||
| + | <blockquote> | ||
| + | <youtube>88yxylibTIw</youtube> | ||
| + | <!-- | ||
| + | <jwplayer width="560" height="440" repeat="true" displayheight="420" | ||
| + | image="http://feynman.mit.edu/8.422/plotobe6.png" | ||
| + | autostart="false">http://feynman.mit.edu/8.422/plotobe6.flv</jwplayer> --> | ||
| + | </blockquote> | ||
| + | |||
| + | === Solutions of the optical Bloch equations === | ||
| + | |||
| + | The optical Bloch equations, describing the evolution of a single atom coupled to the vacuum, | ||
| + | :<math> | ||
| + | \dot{\rho} = -\frac{i}{\hbar}[H,\rho] | ||
| + | -\frac{\Gamma}{2} \left[ { \sigma_+ \sigma_- \rho - 2 \sigma_- \rho \sigma_+ | ||
| + | + \rho \sigma_+ \sigma_- } \right] | ||
| + | \,, | ||
| + | </math> | ||
| + | are a set of three coupled differential equations, | ||
| + | :<math>\begin{array}{rcl} | ||
| + | \dot{r}_x &=& \delta\, r_y - \frac{\Gamma}{2} r_x | ||
| + | \\ \dot{r}_y &=& -\delta\, r_x - \Omega\, r_z - \frac{\Gamma}{2} r_y | ||
| + | \\ \dot{r}_z &=& \Omega\, r_y - \Gamma (r_z +1) | ||
| + | \,. | ||
| + | \end{array}</math> | ||
| + | written in the rotating frame of the atom's Hamiltonian. These equations can be solved analytically, but a great deal of intuition can be obtained from just studying the solutions in several limits. Here, we consider the steady state, transient, and weak excitation limits. | ||
| + | |||
| + | ==== Transient response of the optical Bloch equations ==== | ||
The optical Bloch equations allow us to study the internal state of | The optical Bloch equations allow us to study the internal state of | ||
the atom as it changes due to the external driving field, and due to | the atom as it changes due to the external driving field, and due to | ||
spontaneous emission. | spontaneous emission. | ||
| + | |||
Starting from the time-independent form of the equations, | Starting from the time-independent form of the equations, | ||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
\dot{r}_x &=& \delta\, r_y - \frac{\Gamma}{2} r_x | \dot{r}_x &=& \delta\, r_y - \frac{\Gamma}{2} r_x | ||
| − | \\ \dot{r}_y &=& -\delta\, r_x - | + | \\ \dot{r}_y &=& -\delta\, r_x - \Omega\, r_z - \frac{\Gamma}{2} r_y |
| − | \\ \dot{r}_z &=& | + | \\ \dot{r}_z &=& \Omega\, r_y - \Gamma (r_z +1) |
| − | \, | + | \,. |
\end{array}</math> | \end{array}</math> | ||
| − | we may note that when <math> | + | we may note that when <math>\Omega\rightarrow 0</math> and at resonance, <math>\delta=0</math>, |
the Bloch vector exhibits pure damping behavior, towards <math>r_z=1</math>, and | the Bloch vector exhibits pure damping behavior, towards <math>r_z=1</math>, and | ||
| − | <math>r_x=r_y=0</math>. | + | <math>r_x=r_y=0</math>. Note that a convenient way to write these differential equations is in matrix form, |
| − | When <math> | + | :<math> |
| + | \dot{\vec{r}} = \left[ \begin{array}{ccc} | ||
| + | {-\Gamma/2}& {\delta} & {0} \\ | ||
| + | {-\delta} & -\Gamma/2 & -\Omega \\ | ||
| + | 0 & \Omega & -\Gamma | ||
| + | \end{array} \right] \vec{r} | ||
| + | + \left[ \begin{array}{c} | ||
| + | 0 \\ 0 \\ -\Gamma \end{array} \right] | ||
| + | </math> | ||
| + | |||
| + | When <math>\Omega\gg \Gamma</math>, Rabi oscillations occur, represnted by rapid | ||
rotations of the Bloch vector about <math>\hat{x}</math>. Since the relaxation | rotations of the Bloch vector about <math>\hat{x}</math>. Since the relaxation | ||
along <math>\hat{y}</math> occurs at rate <math>\Gamma/2</math>, and the relaxation about | along <math>\hat{y}</math> occurs at rate <math>\Gamma/2</math>, and the relaxation about | ||
| Line 279: | Line 287: | ||
field would be <math>(\Gamma+\Gamma/2)/2 = 3\Gamma/4</math>. The remaining | field would be <math>(\Gamma+\Gamma/2)/2 = 3\Gamma/4</math>. The remaining | ||
component <math>r_x</math> does not rotate, because it sits along <math>\hat{x}</math>, the | component <math>r_x</math> does not rotate, because it sits along <math>\hat{x}</math>, the | ||
| − | axis of rotation. Thus, it relaxes with rate <math>\Gamma/2</math>. Computation | + | axis of rotation. Thus, it relaxes with rate <math>\Gamma/2</math>. [http://cua.mit.edu/wikipost/20090303-132628/transient.pdf Computation of the eigenvalues] of the equations of motion verify this qualitative |
| − | of the eigenvalues of the equations of motion verify this qualitative | + | picture, and show that for <math>\Omega\gg \Gamma</math>, and <math>\delta=0</math>, the |
| − | picture, and show that for <math> | + | eigenvalues of motion are <math>\pm i\Omega + 3\Gamma/4</math> and <math>-\Gamma/2</math>. |
| − | eigenvalues of motion are <math>\pm | + | |
| + | These | ||
correspond to a main peak at <math>\omega_0</math> with width <math>\Gamma/2</math>, and two | correspond to a main peak at <math>\omega_0</math> with width <math>\Gamma/2</math>, and two | ||
sidebands at <math>\omega_0\pm \Omega</math>, with widths <math>3\Gamma/4</math>, thus | sidebands at <math>\omega_0\pm \Omega</math>, with widths <math>3\Gamma/4</math>, thus | ||
explaining the widths of the observed Mollow triplet lines. | explaining the widths of the observed Mollow triplet lines. | ||
| − | === Steady-state solution of the optical Bloch equations === | + | ==== Steady-state solution of the optical Bloch equations ==== |
The steady state solution of the optical Bloch equations are found by | The steady state solution of the optical Bloch equations are found by | ||
setting all the time derivatives to zero, giving a set of three | setting all the time derivatives to zero, giving a set of three | ||
simultaneous equations, | simultaneous equations, | ||
| + | Starting from the time-independent form of the equations, | ||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
| − | 0 &=& \delta\, | + | 0 &=& \delta\, r^{st}_y - \frac{\Gamma}{2} r^{st}_x |
| − | \\ 0 &=& -\delta\, | + | \\ 0 &=& -\delta\, r^{st}_x - \Omega\, r^{st}_z - \frac{\Gamma}{2} r^{st}_y |
| − | \\ 0 &=& | + | \\ 0 &=& \Omega\, r^{st}_y - \Gamma (r^{st}_z +1) |
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| − | The solutions are | + | The solutions are: |
| − | + | :<math>\begin{align} | |
| − | :<math>\begin{ | + | r^{st}_x &= (\Omega\delta) \frac{1}{\delta^2 + \Omega^2/2 + (\Gamma/2)^2} |
| − | |||
\\ | \\ | ||
| − | + | r^{st}_y &= \left(\frac{\Omega\Gamma}{2}\right) \frac{1}{\delta^2 + \Omega^2/2 + (\Gamma/2)^2} | |
\\ | \\ | ||
| − | + | r^{st}_z &= -\left(\delta^2+\frac{\Gamma^2}{4}\right) \frac{1}{\delta^2 + \Omega^2/2 + (\Gamma/2)^2} | |
| − | \end{ | + | \end{align}</math> |
| − | Physically, these are Lorentzians; the <math> | + | |
| + | Physically, these are Lorentzians; the <math>r^{st}_y</math> solution (the component | ||
in quadrature with the dipole) corresponds to an absorption curve with | in quadrature with the dipole) corresponds to an absorption curve with | ||
half-width | half-width | ||
:<math> | :<math> | ||
| − | \sqrt{\frac{\Gamma^2}{4}+\frac{ | + | \sqrt{\frac{\Gamma^2}{4}+\frac{\Omega^2}{2}} |
\,, | \,, | ||
</math> | </math> | ||
| − | and the <math> | + | and the <math>r^{st}_x</math> solution (the component in-phase with the dipole) |
corresponds to a dispersion curve. And under a strong driving field, | corresponds to a dispersion curve. And under a strong driving field, | ||
| − | as <math> | + | as <math>\Omega\rightarrow\infty</math>, <math>r^{st}_z\rightarrow 0</math>, indicating that the |
populations in the excited and ground states are equalizing. The | populations in the excited and ground states are equalizing. The | ||
steady-state population in the excited state is | steady-state population in the excited state is | ||
:<math> | :<math> | ||
| − | \ | + | \rho^{st}_{ee} = \frac{1+r^{st}_z}{2} = \frac{\Omega^2/4}{\delta^2+\Omega^2/2+\Gamma^2/4} |
\,, | \,, | ||
</math> | </math> | ||
an important result that will later be used in studying light forces. | an important result that will later be used in studying light forces. | ||
| + | |||
| + | <!-- | ||
| + | Here are plots of these solutions, as a function of detuning, for a range of values of <math>\Gamma</math>: | ||
| + | <blockquote> | ||
| + | <jwplayer width="877" height="700" repeat="true" displayheight="680" | ||
| + | image="http://feynman.mit.edu/8.422/steadyobe3.png" | ||
| + | autostart="false">http://feynman.mit.edu/8.422/steadyobe3.flv</jwplayer> | ||
| + | </blockquote> | ||
| + | --> | ||
| + | |||
These solutions can be re-expressed in a simplified manner by defining | These solutions can be re-expressed in a simplified manner by defining | ||
the saturation parameter | the saturation parameter | ||
:<math> | :<math> | ||
| − | s = \frac{ | + | s = \frac{\Omega^2/2}{\delta^2+\Gamma^2/4} |
\,, | \,, | ||
</math> | </math> | ||
in terms of which we find | in terms of which we find | ||
| − | :<math>\begin{ | + | :<math>\begin{align} |
| − | + | r^{st}_x &= \frac{2\delta}{\Omega} \frac{s}{1+s} | |
\\ | \\ | ||
| − | + | r^{st}_y &= \frac{\Gamma}{\Omega} \frac{s}{1+s} | |
\\ | \\ | ||
| − | + | r^{st}_z &= -\frac{1}{1+s} | |
\,. | \,. | ||
| − | \end{ | + | \end{align}</math> |
| − | As <math>s\rightarrow \infty</math>, the atomic transitions become | + | As <math>s\rightarrow \infty</math>, the atomic transitions become [[Saturation of atomic transitions|saturated]], and the linewidth of the transition broadens from its |
| − | saturated | ||
natural value <math>\Gamma</math>, becoming <math>\Gamma' = \Gamma\sqrt{1+s}</math> on | natural value <math>\Gamma</math>, becoming <math>\Gamma' = \Gamma\sqrt{1+s}</math> on | ||
resonance, at <math>\delta=0</math>. | resonance, at <math>\delta=0</math>. | ||
| + | |||
| + | Here are plots of the steady state solution for varying <math>\Omega/\Gamma</math>: | ||
| + | <blockquote> | ||
| + | <youtube>jT323V-PTwQ</youtube> | ||
| + | <!-- | ||
| + | <jwplayer width="560" height="440" repeat="true" displayheight="420" | ||
| + | image="http://feynman.mit.edu/8.422/steady4.png" | ||
| + | autostart="false">http://feynman.mit.edu/8.422/steady4.flv</jwplayer> --> | ||
| + | </blockquote> | ||
| + | |||
| + | ==== Weak excitation limit solution of the optical Bloch equations ==== | ||
| + | |||
| + | Once again, the time-independent form of the optical Bloch equations is | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | \dot{\rho}_{ee} &= i\frac{\Omega}{2}(\rho_{eg}-\rho_{ge}) | ||
| + | - \Gamma\rho_{ee} | ||
| + | \\ | ||
| + | \dot{\rho}_{ge} &= -i\delta\rho_{ge} - | ||
| + | i\frac{\Omega}{2}(\rho_{ee}-\rho_{gg}) | ||
| + | - \frac{\Gamma}{2} \rho_{ge} | ||
| + | \,, | ||
| + | \end{align} | ||
| + | </math> | ||
| + | where the remaining two components of the density matrix are given by | ||
| + | <math>\rho_{gg} = 1-\rho_{ee}</math>, and <math>\rho_{eg} = \rho_{ge}^*</math>. It is | ||
| + | insightful to study these equations in the limit of weak excitation, | ||
| + | and for short evolution times. | ||
| + | |||
| + | It turns out that the solution of these equations to lowest order | ||
| + | in <math>|\Omega|</math>, and in the limit <math>|\Omega|\ll\Gamma</math>, with the initial | ||
| + | conditions <math>\rho_{ee}=0</math> and <math>\rho_{ge}=0</math>, gives | ||
| + | :<math> | ||
| + | \rho_{ee} = | ||
| + | \frac{\frac{1}{4}|\Omega|^2}{\delta^2+\left(\frac{\Gamma}{2}\right)^2} | ||
| + | \left[{ 1+e^{-\Gamma t}-2\cos(\delta t)e^{-\Gamma t/2}}\right] | ||
| + | \,. | ||
| + | </math> | ||
| + | |||
| + | Moreover the solution of these equations to lowest order in | ||
| + | <math>|\Omega|</math> in the limit <math>|\Omega|t\ll 1</math>, with the initial conditions <math>\rho_{ee}=0</math> and <math>\rho_{ge}=0</math>, gives | ||
| + | :<math> | ||
| + | \rho_{ee} = \frac{1}{4}|\Omega|^2 t^2 | ||
| + | \,, | ||
| + | </math> | ||
| + | irrespective of the values of <math>(\omega_0-\omega_L)</math> and <math>\Gamma</math>. | ||
| + | |||
| + | === Damped vacuum Rabi oscillations === | ||
| + | |||
| + | {{:Damped vacuum Rabi oscillations}} | ||
== References == | == References == | ||
[[Category:Optical Bloch Equations]] | [[Category:Optical Bloch Equations]] | ||
Latest revision as of 23:37, 3 April 2017
The optical Bloch equations
provide a time-dependent quantum description of a spontaneously emitting atom driven by a classical electromagnetic field. Considerable insight into the physical processes involved can be gained by studying these equations in the transient excitation limit, as well as the steady-state limit, as we see in this section. We begin by considering the coherent part of the evolution, then extend this to re-visit the Bloch sphere picture of the optical Bloch equations, which provides useful visualizations of transient responses and steady state solutions. Finally, we return to vacuum Rabi oscillations and investigate how cavity loss leads to damping of the oscillations, as an illustration of master equations which are more general than the optical Bloch equation.
Contents
Eigenstates of the Jaynes-Cummings Hamiltonian
The Hamiltonian involved in the optical Bloch equations,
describes the evolution of an atom in a classical field. We begin here by reviewing the coherent evolution under .
arises from the Jaynes-Cummings interaction we have previously considered in the context of cavity QED, describing a single two-level atom interacting with a single mode of the electromagnetic field:
The last term in this expression is , the dipole interaction between atom and field. By defining and , we may write this interaction as
In the frame of reference of the atom and field, recall that
When near resonance, , and because the and terms oscillate at nearly twice the frequency of , those terms can be dropped. Doing so is known as the rotating wave approximation, and it gives us a simplified interaction Hamiltonian
Under this approximation, it is useful to note that this interaction merely exchanges one quantum of excitation from atom to field, and back, so that the total number of excitations is a constant of the motion. We may thus write the total Hamiltonian, in the rotating frame with the rotating wave approximation, as
where we have defined , and . Below, we may use to simplify writing.
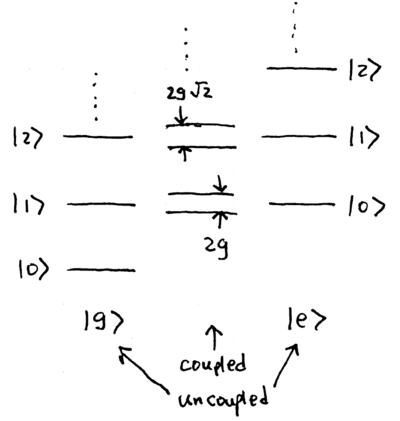
What are the eigenstates of this Hamiltonian? It describes a two-level system coupled to a simple harmonic oscillator; when uncoupled, if , then the eigenstates are simply those of , and , as shown here:
When coupled, degenerate energy levels split (this is sometimes called dynamimc Stark splitting), with harmonic oscillator levels and splitting into two energy levels separated by . Since the coupling only pairs levels separated by one quantum of excitation, it is straightforward to show that the eigenstates of the Jaynes-Cummings Hamiltonian fall into well defined pairs of states, which we may label as ; these are
and they have energies
When , similar physics result, but with slightly more complicated expressions describing the eigenstates, as we shall see when we later return to the "dressed states" picture.
Strongly driven atom: Mollow triplet
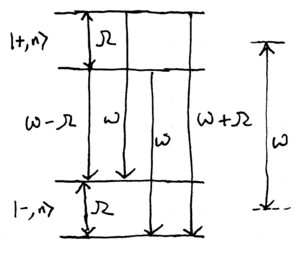
An atom strongly coupled to a single mode electromagnetic field, or an atom driven strongly by a single mode field, will thus have an emission spectrum described by the coupled energy level diagram:
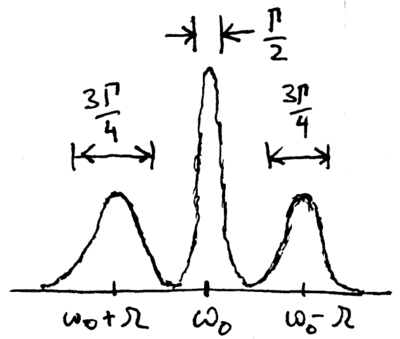
where, to good approximation, the energy level differences are and . These three lines which appear in the spectrum are known as the Mollow triplet:
The Mollow triplet is experimentally observed in a wide variety of systems. However, while our energy eigenstate analysis has predicted the number and frequencies of the emission lines, it fails to explain a key characteristic: the widths are not the same. If the central peak at has width HWHM , the two sidebands each have a HWHM of . To explain this, we need the optical Bloch equations.
Optical Bloch equation evolution on the Bloch sphere
Let's examine the case of a two-level atom with an excited state with linewdith that can decay to the ground state . We'll use the following conventions
- Failed to parse (syntax error): {\displaystyle |0{\rangle}=|e{\rangle} = \left[ \begin{array}{cc}{1}\\{0}\end{array}\right], |1{\rangle}=|g{\rangle} = \left[ \begin{array}{cc}{0}\\{1}\end{array}\right], \rho = \left[ \begin{array}{cc}{\rho_{ee}}&{\rho_{eg}}\\{\rho_{ge}}&{\rho_{gg}}\end{array} \right] \\ X = \left[ \begin{array}{cc}{0}&{1}\\{1}&{0}\end{array} \right] , Y = \left[ \begin{array}{cc}{0}&{-i}\\{i}&{0}\end{array} \right] , Z = \left[ \begin{array}{cc}{1}&{0}\\{0}&{-1}\end{array} \right], \sigma_+ = \left[ \begin{array}{cc}{0}&{1}\\{0}&{0}\end{array} \right], \sigma_- = \left[ \begin{array}{cc}{0}&{0}\\{1}&{0}\end{array} \right] \,, }
Recall that the optical Bloch equation is
and the rotating frame Hamiltonian (as derived in AMO I Resonances) is
Substituting these matrices into the optical Bloch equation and evaluating the right had side gives us the equations of motion
As a quick sanity check, we see that and as you would expect from taking the time derivative of the normalization condition and the hermicity requirement . Furthermore is purely real, which means that the time derivatives of and are purely real, which in turn means that and stay purely real as the density matrix evolves.
Visualization: Bloch vector
This seemingly complicated evolution of the density matrix is easier to understand when visualized on the Bloch sphere. We have previously seen that an arbitrary qubit state can be represented as being a point on a unit sphere, located at in polar coordinates. Similarly, a density matrix may be depicted as being a point inside or on the unit sphere, using
where is the Bloch vector representation of . Writing out both sides of that expression allows us to see how the Bloch vector components are related to the elements of the density matrix
And these relations can easily be reversed to find
We can then use these relations to rewrite the above differential equations for the elements of the density matrix into differential equations for the components of the Bloch vector. This gives
Note how these equations of motion provide a simple set of flows on the Bloch sphere: the terms correspond to a rotation in the plane, corresponds to a rotation in the plane, and drives a relaxation process which shrinks and components of the Bloch vector, while moving the component toward .
Physics: in-phase and quadrature components
Physically, what is the meaning of , , and ? is manifestly the population difference between the excited and ground states. The other two components may be interpreted by recognizing that the average dipole moment of the atom is
Thus, and correspond to the phase components of the atomic dipole moment which are in-phase and in quadrature with the incident electromagnetic field.
Animation of full solutions
Here are plots of the full solutions of the optical Bloch equations on the Bloch sphere, for various cases of , , and (sample matlab files to solve the differential equations: obefun1.m plotobe2.m). In this video we have the ground state at the top of the Bloch sphere and the frequencies are given relative to
<youtube>88yxylibTIw</youtube>
Solutions of the optical Bloch equations
The optical Bloch equations, describing the evolution of a single atom coupled to the vacuum,
are a set of three coupled differential equations,
written in the rotating frame of the atom's Hamiltonian. These equations can be solved analytically, but a great deal of intuition can be obtained from just studying the solutions in several limits. Here, we consider the steady state, transient, and weak excitation limits.
Transient response of the optical Bloch equations
The optical Bloch equations allow us to study the internal state of the atom as it changes due to the external driving field, and due to spontaneous emission.
Starting from the time-independent form of the equations,
we may note that when and at resonance, , the Bloch vector exhibits pure damping behavior, towards , and . Note that a convenient way to write these differential equations is in matrix form,
When , Rabi oscillations occur, represnted by rapid rotations of the Bloch vector about . Since the relaxation along occurs at rate , and the relaxation about occurs at rate , we might expect that the average relaxation rate of the rotating components under such a strong driving field would be . The remaining component does not rotate, because it sits along , the axis of rotation. Thus, it relaxes with rate . Computation of the eigenvalues of the equations of motion verify this qualitative picture, and show that for , and , the eigenvalues of motion are and .
These correspond to a main peak at with width , and two sidebands at , with widths , thus explaining the widths of the observed Mollow triplet lines.
Steady-state solution of the optical Bloch equations
The steady state solution of the optical Bloch equations are found by setting all the time derivatives to zero, giving a set of three simultaneous equations, Starting from the time-independent form of the equations,
The solutions are:
Physically, these are Lorentzians; the solution (the component in quadrature with the dipole) corresponds to an absorption curve with half-width
and the solution (the component in-phase with the dipole) corresponds to a dispersion curve. And under a strong driving field, as , , indicating that the populations in the excited and ground states are equalizing. The steady-state population in the excited state is
an important result that will later be used in studying light forces.
These solutions can be re-expressed in a simplified manner by defining
the saturation parameter
in terms of which we find
As , the atomic transitions become saturated, and the linewidth of the transition broadens from its natural value , becoming on resonance, at .
Here are plots of the steady state solution for varying :
<youtube>jT323V-PTwQ</youtube>
Weak excitation limit solution of the optical Bloch equations
Once again, the time-independent form of the optical Bloch equations is
where the remaining two components of the density matrix are given by , and . It is insightful to study these equations in the limit of weak excitation, and for short evolution times.
It turns out that the solution of these equations to lowest order in , and in the limit , with the initial conditions and , gives
Moreover the solution of these equations to lowest order in in the limit , with the initial conditions and , gives
irrespective of the values of and .
Damped vacuum Rabi oscillations
The optical Bloch equations can be generalized to describe not just an atom interacting with the vacuum, but also an atom and a single cavity mode, each interacting with its own reservoir. This is the master equation for cavity QED, and using such a master equation we can revisit the phenomenon of vacuum Rabi oscillations and see what happens in the presence of damping.
Generalization of the optical Bloch equations
The starting point for generalizing the optical Bloch equations is the Lindblad form we previously saw in the full-derivation walkthrough,
In this expression, and are "jump operators," and represent changes that occur to the atom when distinct dissipative events happen ("distinct" meaning that the environment changes between orthogonal states).
We may write the master equation for our more general scenario by replacing the atomic density matrix by a general density matrix representing the atom and cavity field, and by replacing the atomic jump operators with general jump operators ,
Note that the include normalization factors which reflect their probabilities of occurrence. In other words, for the atom + vacuum model, .
Master equation for cavity QED system
For the cavity QED model, the atom and cavity field each have possible jump operators. In general, the atom and cavity may both couple to a thermal field with average photons. In such a case, the jump operators are , , , and , where parameterizes the spontaneous emission rate of the atom in free space, and is parameterizes the cavity factor.
Experimentally, typically the environment, the vacuum, is essentially at zero temperature, so , in which case the only two relevant jump operators are and .
Damped vacuum Rabi oscillations
Vacuum Rabi oscillations, in the absence of damping, involve only two states of the atom and cavity: and . When damping is added, the state must be included, since both the atom and cavity states can decay and loose their quanta of energy. Moreover, because only one quantum of excitation is involved in this system, we can observe the essential physics by considering the case when is zero (no spontaneous emission), but is nonzero (the cavity is leaky). Let be the vacuum Rabi frequency, and denote this three state space by , , and . Written out explicitly in terms of the density matrix elements , the master equation is (for the case with the system starting in the state )
When the cavity damping rate is small, , then the vacuum Rabi oscillations are damped, with average damping rate since the atoms spend roughly half their time in the excited state.
When the cavity damping rate is large, , then the atomic excitation is irreversibly damped, and no oscillations occur. Let be the probability of being in the state. We can combine two of the above equations to write
Since in this case , and , it follows that
Since in this regime, we slowly try to populate state while it quickly decays away, we can approximate giving
Finally plugging this back into the optical bloch equation for yields
so decays exponentially, with rate . Note that a large cavity damping rate slows down the decay of the atom's excited state. This is due to the fact that the stimulated transition (Rabi oscillation) to the lower state is slowed down by the cavity damping (which is a manifestation of the quantum Zeno effect).
Purcell factor: cavity enhanced spontaneous emission
How does this compare with the free space spontaneous emission rate ? Recall that the vacuum Rabi frequency is (for the case that the dipole matrix element vector and cavity mode polarization are aligned)
where is the atomic dipole moment and is the electric field amplitude of a single photon at the atomic transition frequency (Note that this is a standing wave in a cavity so it is a factor of two larger than the field for a running wave),
and is the cavity volume. This gives
Letting , we thus find that
as the decay rate of the atom in the cavity.
Recall that the spontaneous emission rate of an atom in free space, as determined by Fermi's golden rule, is
The ratio of this rate to the decay rate in the cavity is
where we take as being the wavelength of the cavity field, which is assumed to be resonant with the atomic transition frequency . Note that is independent of the atomic dipole strength, and determined solely by cavity parameters. Moreover, note that for small, high- cavities, the decay rate of the atom in the cavity can be much larger than the free space spontaneous emission rate. This "cavity enhanced" spontaneous emission rate was predicted by Purcell (1946), an observation credited as being the starting point of cavity QED.
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604d2158dbbebf16674738f973827dbb18e3a819)


![{\displaystyle H_{JC}={\frac {\hbar \omega _{0}}{2}}\left[{|e\rangle \langle e|-|g\rangle \langle g|}\right]+\hbar \omega a^{\dagger }a+{\frac {\hbar \Omega }{2}}\left[{|g\rangle \langle e|+|e\rangle \langle g|}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/630609e3aab033690555f530c6e4323ba84a5538)



![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{\sigma _{+}+\sigma _{-}}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3410ceeb8ffe707f367fc599209a8dad817b08df)





![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{a^{\dagger }\sigma _{-}+a\sigma _{+}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60d32887d250fa22239d00c10278b510514772e)












![{\displaystyle |\pm ,n\rangle ={\frac {1}{\sqrt {2}}}\left[{|e,n\rangle \pm |g,n+1\rangle }\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55f08b48a6a98c378c7ba35aff03487dd1c3463e)









![{\displaystyle H={\frac {\hbar }{2}}\left(-\delta Z+\Omega X\right)={\frac {\hbar }{2}}\left[{\begin{array}{cc}{-\delta }&{\Omega }\\{\Omega }&{\delta }\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/492a8aba8b716785e12c716ce476c423a1444b73)































![{\displaystyle {\dot {\vec {r}}}=\left[{\begin{array}{ccc}{-\Gamma /2}&{\delta }&{0}\\{-\delta }&-\Gamma /2&-\Omega \\0&\Omega &-\Gamma \end{array}}\right]{\vec {r}}+\left[{\begin{array}{c}0\\0\\-\Gamma \end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a580cad68617ecfb286f1dd0bf82375e72f0868f)

























![{\displaystyle \rho _{ee}={\frac {{\frac {1}{4}}|\Omega |^{2}}{\delta ^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}\left[{1+e^{-\Gamma t}-2\cos(\delta t)e^{-\Gamma t/2}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c19bf5cb1660757c54d1ccc65a9f0c4cbfcd57fe)



![{\displaystyle {\dot {\rho }}_{A}=-{\frac {i}{\hbar }}[H,\rho _{A}]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho _{A}-2\sigma _{-}\rho _{A}\sigma _{+}+\rho _{A}\sigma _{+}\sigma _{-}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13bf26eb3d88c4444078e147d8e6751295dea1fd)




![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]+\sum _{k}\left[{L_{k}\rho L_{k}^{\dagger }-{\frac {1}{2}}(L_{k}^{\dagger }L_{k}\rho +\rho L_{k}^{\dagger }L_{k})}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f41a3c9853e8923bf9cfd246f4affa45f6e6039a)
















































