A single photon, mathematically represented by the number eigenstate
 , physically describes the electromagnetic field corresponding
to the lowest nonzero energy eigenstate of a single mode cavity.
, physically describes the electromagnetic field corresponding
to the lowest nonzero energy eigenstate of a single mode cavity.
 is the vacuuum state.
A great deal of physics can be understood by considering what happens
to just the
is the vacuuum state.
A great deal of physics can be understood by considering what happens
to just the  and
and  states, through a variety of optical
components. This section uses such an approach to explore three of
the most basic components -- two linear components: phase shifters,
beam splitters, and one nonlinear component: Kerr cross-phase
modulation. These are the building blocks of linear and non-linear
interferometers; their physical behavior provides helpful intuition
for quantum behavior.
states, through a variety of optical
components. This section uses such an approach to explore three of
the most basic components -- two linear components: phase shifters,
beam splitters, and one nonlinear component: Kerr cross-phase
modulation. These are the building blocks of linear and non-linear
interferometers; their physical behavior provides helpful intuition
for quantum behavior.
Beamsplitters and phase shifters
The number state  evolves through propagation in free space to
become
evolves through propagation in free space to
become  after time
after time  . In a medium with a
different index of refraction, however, light propagates at a
different velocity, giving, for example,
. In a medium with a
different index of refraction, however, light propagates at a
different velocity, giving, for example,  .
Such a phase difference is only physically meaningful, however, when
compared with a reference. Let us therefore introduce a pair of
modes, each with either
.
Such a phase difference is only physically meaningful, however, when
compared with a reference. Let us therefore introduce a pair of
modes, each with either  or
or  photons, depicted as two lines, and
using a box to indicate a segment through which one mode propagates at
a different velocity. For example:
photons, depicted as two lines, and
using a box to indicate a segment through which one mode propagates at
a different velocity. For example:
depicts two modes, in which the top photon has its phase shifted by
 relative to the bottom one. It is clear that any relative phase
shift can be imparted between the two modes, by an appropriate
experimental setup; experimentally, this can be accomplished with
different thicknesses of glass, or by lengthening one path versus the
other.
relative to the bottom one. It is clear that any relative phase
shift can be imparted between the two modes, by an appropriate
experimental setup; experimentally, this can be accomplished with
different thicknesses of glass, or by lengthening one path versus the
other.
Two modes of light can be mixed by a beamsplitter (as we have
previously seen). A beamsplitter  acts with Hamiltonian
acts with Hamiltonian

on the two modes, with corresponding operators  and
and  .
Transformation of light through this beamsplitter is given by
.
Transformation of light through this beamsplitter is given by
 , where
, where  is the angle of the beamsplitter,
giving the unitary operation
is the angle of the beamsplitter,
giving the unitary operation
![{\displaystyle B=\exp \left[{\theta \left({a^{\dagger }b-ab^{\dagger }}\right)}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cde964c0c37431a84260835508da295a53bd5290)
We may depict this as:
Note the use of a  to distinguish the ports; this is needed
because we have adopted a phase convention for the beamsplitter which
obviates the need to keep track of an extra factor of
to distinguish the ports; this is needed
because we have adopted a phase convention for the beamsplitter which
obviates the need to keep track of an extra factor of  . In the
Heisenberg picture,
. In the
Heisenberg picture,  transforms
transforms  and
and  as
as

This can be verified using the the Baker--Campbell--Hausdorf formula,

where  is a complex number,
is a complex number,  ,
,  , and
, and  are operators, and
are operators, and
 is defined recursively as the sequence of commutators
is defined recursively as the sequence of commutators  ,
, ![{\displaystyle C_{1}=[G,C_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f83df0933d6a3c3706b351c36fb81538515a85b9) ,
, ![{\displaystyle C_{2}=[G,C_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6157b6fd985b0ff55033671895f6dccd4a5d81) ,
, ![{\displaystyle C_{3}=[G,C_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb7b38ae279f6651995a6a493bacfe81b34c5880) ,
,  ,
, ![{\displaystyle C_{n}=[G,C_{n-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9d20f4ef4def8f2300f808179588f8bfdbf739f) .
.
Since it follows from ![{\displaystyle [a,a^{\dagger }]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/671da8b1eb59fe1c04e601cc7963a6511d88c74e) and
and ![{\displaystyle [b,b^{\dagger }]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ffc8deb8c5daa77fae70826f05172239777e632) that
that ![{\displaystyle [G,a]=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c839dfe2562400194bd40409990af8c8105a447f) and
and
![{\displaystyle [G,b]=-a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e66ece5d36dd8598163277d2bf53cc526ae88e9) , for
, for  , we obtain for the expansion
of
, we obtain for the expansion
of  the series coefficients
the series coefficients  ,
, ![{\displaystyle C_{1}=[G,a]=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3abeae2e5e7f5457bbed75f80bbf6ed33383864) ,
,
![{\displaystyle C_{2}=[G,C_{1}]=-a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ad248c8f33c48531a9cc5c09f1b481560f63e05) ,
, ![{\displaystyle C_{3}=[G,C_{2}]=-[G,C_{0}]=-b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b328c9d224959a15fe187a32c21e8acd51a7ffd0) , which in general are
, which in general are

From this, our desired result follows straightforwardly:

The transform  is trivially found by swapping
is trivially found by swapping  and
and  in the
above solution.
in the
above solution.
Beamsplitters with single photon inputs
How does  act on a single photon input? On input
act on a single photon input? On input  , letting
the modes be
, letting
the modes be  on the right, and
on the right, and  on the left, we get
on the left, we get

Similarly,  . This
indicates that
. This
indicates that  corresponds to a
corresponds to a  beamsplitter.
Note that
beamsplitter.
Note that  does not destroy any photons; it can only move them
between the two modes. Mathamatically, this arises from the fact that
it commutes with the total photon number operator,
does not destroy any photons; it can only move them
between the two modes. Mathamatically, this arises from the fact that
it commutes with the total photon number operator,  .
.
If both input modes contain photons, the output state does not have as
simple a form as above. In particular, we find that

so it is possible for the output to be found to have both photons in
one mode. Since we'd like to avoid such cases in this section, let us
restrict our attention here to the case when inputs to beampsplitters
have a total of one photon at most.
Dual-rail photon states and two-level systems
Omitting the vacuum state  , the two-mode state space we shall
consider thus has a basis state spanned by
, the two-mode state space we shall
consider thus has a basis state spanned by  , and
, and  . We
call this the dual-rail photon state space (this Hilbert space behaves much like a a two-level system). Note that an
arbitrary state in this space as
. We
call this the dual-rail photon state space (this Hilbert space behaves much like a a two-level system). Note that an
arbitrary state in this space as  , where
, where  and
and  are complex numbers satisfying
are complex numbers satisfying
 .
.
From Bloch's Theorem, it follows that any dual-rail photon state can
be generated using phase shifters and beamsplitters. Specifically,
if we write  as a two-component vector, then the action of
as a two-component vector, then the action of  is
is
![{\displaystyle B(\theta )\left[{\begin{array}{c}{\alpha }\\{\beta }\end{array}}\right]=\left[{\begin{array}{cc}{\cos \theta }&{-\sin \theta }\\{\sin \theta }&{\cos \theta }\end{array}}\right]\left[{\begin{array}{c}{\alpha }\\{\beta }\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbd7073849d13faa33b118bd924076ccde2ef741)
Similarly, the action of a phase shifter  of phase
of phase  is
is
![{\displaystyle P(\phi )\left[{\begin{array}{c}{\alpha }\\{\beta }\end{array}}\right]=e^{-i\theta /2}\left[{\begin{array}{cc}{e^{i\theta /2}}&{0}\\{0}&{e^{-i\theta /2}}\end{array}}\right]\left[{\begin{array}{c}{\alpha }\\{\beta }\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23b28130466753154f3e728eff05df125e6f33ac)
where the overall phase  is irrelevant and can be
dropped in the following. Let us define the Pauli matrices as
is irrelevant and can be
dropped in the following. Let us define the Pauli matrices as
![{\displaystyle {\begin{array}{rcl}X&=&\left[{\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}}\right]\\Y&=&\left[{\begin{array}{cc}{0}&{-i}\\{i}&{0}\end{array}}\right]\\Z&=&\left[{\begin{array}{cc}{1}&{0}\\{0}&{-1}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f4c4dc132ee998872269c6b90b2cac55933dcdc)
In terms of these, we find that the phase shifter and beamsplitter
operators may be expressed as
![{\displaystyle {\begin{array}{rcl}B(\theta )&=&\exp \left[{i\theta Y}\right]\\P(\phi )&=&\exp \left[{i\phi Z/2}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed1c798b58ec2107ccfe2fb5b482d0433eb05ea)
These are rotations of a two-level system, about the axes
 and
and  , by angles
, by angles  and
and  ,
respectively. The standard rotation operator definitions are
,
respectively. The standard rotation operator definitions are
![{\displaystyle {\begin{array}{rcl}R_{x}(\theta )&\equiv &e^{-i\theta X/2}=\cos {\frac {\theta }{2}}I-i\sin {\frac {\theta }{2}}X=\left[{\begin{array}{cc}\cos {\frac {\theta }{2}}&-i\sin {\frac {\theta }{2}}\\-i\sin {\frac {\theta }{2}}&\cos {\frac {\theta }{2}}\end{array}}\right]\\R_{y}(\theta )&\equiv &e^{-i\theta Y/2}=\cos {\frac {\theta }{2}}I-i\sin {\frac {\theta }{2}}Y=\left[{\begin{array}{cc}\cos {\frac {\theta }{2}}&-\sin {\frac {\theta }{2}}\\\sin {\frac {\theta }{2}}&\cos {\frac {\theta }{2}}\end{array}}\right]\\R_{z}(\theta )&\equiv &e^{-i\theta Z/2}=\cos {\frac {\theta }{2}}I-i\sin {\frac {\theta }{2}}Z=\left[{\begin{array}{cc}e^{-i\theta /2}&0\\0&e^{i\theta /2}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87225207af366d9d68d1998719ba6d411b5dace3)
Bloch's Theorem
In terms of these, Bloch's Theorem states the following:
Proof:~
Since  is unitary, the rows and columns of
is unitary, the rows and columns of  are orthonormal, from which
it follows that there exist real numbers
are orthonormal, from which
it follows that there exist real numbers  ,and
,and  such that
such that
![{\displaystyle {\begin{array}{rcl}U=\left[{\begin{array}{cc}e^{i(\alpha -\beta /2-\delta /2)}\cos {\frac {\gamma }{2}}&-e^{i(\alpha -\beta /2+\delta /2)}\sin {\frac {\gamma }{2}}\\e^{i(\alpha +\beta /2-\delta /2)}\sin {\frac {\gamma }{2}}&e^{i(\alpha +\beta /2+\delta /2)}\cos {\frac {\gamma }{2}}\end{array}}\right].\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cdffa723507b330398ac45f72d11c6d7247cbd5)
Equation (\ref{eqtn:alg:qubit_decomp}) now follows immediately from the
definition of the rotation matrices and matrix multiplication.
What we have just done, expressed in modern language, is to introduce
an optical quantum bit, a "qubit," and showed that arbitrary
single qubit operations ("gates") can be performed using
phase-shifters and beamsplitters.
For example, one widely useful single-qubit transform is the Hadamard
gate,
![{\displaystyle {\begin{array}{rcl}H={\frac {1}{\sqrt {2}}}\left[{\begin{array}{cc}{1}&{1}\\{1}&{-1}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f26d09a9191a1aa422af968868ed8ff0ea03c7)
This operation can be performed by doing:
where the beamsplitter has  . From inspection, it is
easy to verify that it transforms
. From inspection, it is
easy to verify that it transforms  and
and  up to an overall phase, as
desired. Up to a phase shift, a
up to an overall phase, as
desired. Up to a phase shift, a  beamsplitter can thus be
thought of as being a Hadamarad gate, and vice-versa.
beamsplitter can thus be
thought of as being a Hadamarad gate, and vice-versa.
Mach-Zehnder interferometer
The reason we have introduced the dual-rail photon representation of a
qubit is because this will allow us to clarify the universality of
certain quantum optical ideas, namely interference and
interferometers, which will be ubiquitous through our treatment of
atoms and quantum information.
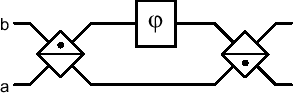
Let us begin by developing a model for the Mach-Zehnder
interferometer, which is constructed from two beamsplitters. Recall
that two beamsplitters  and
and  , configured as
, configured as
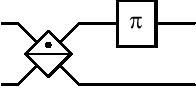
naturally leave the output identical to the input, as  .
If a phase shifter
.
If a phase shifter  is placed inbetween two
is placed inbetween two  beamsplitters,
beamsplitters,
then the input is transformed by
![{\displaystyle {\begin{array}{rcl}{B}^{\dagger }(\pi /4)P(\phi )B(\pi /4)&=&\exp \left[{-i\pi Y/4}\right]\exp \left[{i\phi Z/2}\right]\exp \left[{i\pi Y/4}\right]\\&=&R_{y}(\pi /2)R_{z}(-\phi )R_{y}(-\pi /2)\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d6da722c294cc51f364863de15b94d011bd159f)
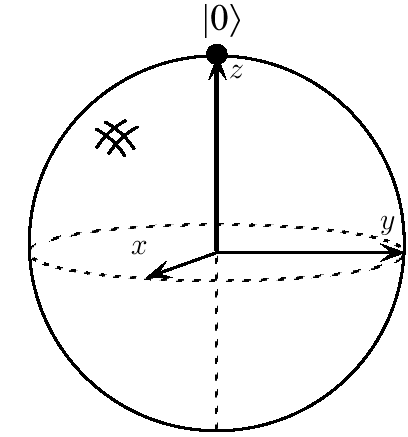
It is convenient to visualize this sequence of three rotations on the
Bloch sphere:
The first  rotates
rotates  into
into  , and
, and
 into
into  . The system is then rotated around
. The system is then rotated around
 by angle
by angle  . Then the last
. Then the last  rotates
rotates
 back to
back to  . The overall sequence is thus a rotation
by
. The overall sequence is thus a rotation
by  about
about  :
:

If the input is  , then the output will thus be
, then the output will thus be
 , so the photon is found in mode
, so the photon is found in mode
 with probability
with probability  , and in mode
, and in mode  with
probability
with
probability  . This is exactly what a classical
interferometer should do. Two important limits are that when
. This is exactly what a classical
interferometer should do. Two important limits are that when  (the interferometer is "balanced"), the input is unchanged, and when
(the interferometer is "balanced"), the input is unchanged, and when
 , the two modes are swapped.
, the two modes are swapped.
Nonlinear Mach-Zehnder interferometer
The two components we have studied so far, phase shifters and
beamsplitters, are linear optics elements. Such elements have
an electric polarization which is linear with the applied electric
field,  . Nonlinear optical
elements, have
. Nonlinear optical
elements, have  . Previously, we have seen
that an optical parametric oscillator (with
. Previously, we have seen
that an optical parametric oscillator (with  ) can be used
for creating quantum states such as squeezed light. What do nonlinear
optical elements do to single photons?
) can be used
for creating quantum states such as squeezed light. What do nonlinear
optical elements do to single photons?
Optical Kerr media
Consider a material with  , which we may
model as having the Hamiltonian
, which we may
model as having the Hamiltonian

where  and
and  describe two modes propagating through the medium.
For a crystal of length
describe two modes propagating through the medium.
For a crystal of length  we obtain the unitary transform
we obtain the unitary transform

Here,  parametrizes the third order nonlinear susceptibility
coefficient. We will refer to
parametrizes the third order nonlinear susceptibility
coefficient. We will refer to  as the Kerr cross-phase
modulation Hamiltonian, and the nonlinear crystal as being a Kerr
medium.
as the Kerr cross-phase
modulation Hamiltonian, and the nonlinear crystal as being a Kerr
medium.
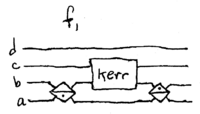
Interferometer with Kerr medium inside
Interesting non-classical behavior can be obtained using
interferometers constructed with Kerr media used as nonlinear phase
shifters. For single photon states, we find that

Let us take  , such that
, such that  .
Suppose we now place the Kerr medium inside a Mach-Zehnder
interferometer in this manner:
.
Suppose we now place the Kerr medium inside a Mach-Zehnder
interferometer in this manner:
\noindent
Intuitively, we expect that when no photons are input into  , then
the Mach-Zehnder interferometer is balanced, leading to
, then
the Mach-Zehnder interferometer is balanced, leading to  and
and  . But when a photon is input into
. But when a photon is input into  , if the cross-phase
modulation due to
, if the cross-phase
modulation due to  is sufficiently large (
is sufficiently large ( ), then the
inputs are swapprd, producing
), then the
inputs are swapprd, producing  and
and  .
.
Mathematically, we may write the transform performed by this nonlinear
Mach-Zehnder interferometer as the unitary transform  ,
where
,
where  is a 50/50 beamsplitter,
is a 50/50 beamsplitter,  is the Kerr cross phase
modulation operator
is the Kerr cross phase
modulation operator  , and
, and  is the product of the coupling constant and the interaction distance.
The transform simplifies to give
is the product of the coupling constant and the interaction distance.
The transform simplifies to give
![{\displaystyle {\begin{array}{rcl}U&=&\exp \left[{i\xi {c}^{\dagger }c\left({\frac {b^{\dagger }-a^{\dagger }}{\sqrt {2}}}\right)\left({\frac {b-a}{\sqrt {2}}}\right)}\right]\\&=&e^{i{\frac {\pi }{2}}{b}^{\dagger }b}\,e^{{\frac {\xi }{2}}{c}^{\dagger }c(a^{\dagger }b-b^{\dagger }a)}\,e^{-i{\frac {\pi }{2}}{b}^{\dagger }b}\,e^{i{\frac {\xi }{2}}{a}^{\dagger }a\,{c}^{\dagger }c}\,e^{i{\frac {\xi }{2}}{b}^{\dagger }b\,{c}^{\dagger }c}\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1ff05608c395719413ce0921bb72fa03bf5b2c)
The first and third exponentials are constant phase shifts, and the last two
phase shifts come from cross phase modulation. All those effects are not
fundamental, and can be compensated for. The interesting term is the second
exponential, which we define as
![{\displaystyle F(\xi )=\exp \left[{{\frac {\xi }{2}}{c}^{\dagger }c\,(a^{\dagger }b-b^{\dagger }a)}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4437ff0a1688cced07348cbd6429a496328cb18)
For  , when no photons are input at
, when no photons are input at  , then
, then  and
and  , but when a single photon is input at
, but when a single photon is input at  , then
, then  and
and  , as we expected. We may also interpret
, as we expected. We may also interpret  as being like a
controlled-beamsplitter operator, where the rotation angle is
as being like a
controlled-beamsplitter operator, where the rotation angle is  .
.
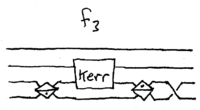
Squeezing with nonlinear interferometer
How does this nonlinear interferometer produce non-classical behavior?
Well, one thing it can be used for is to create a state very much like
two-mode squeezed light, as we now show in the limit of single
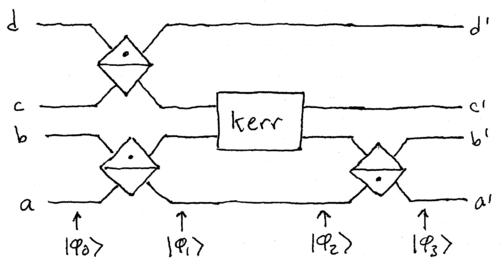
photons. Consider this setup, with two dual-rail qubits, and one Kerr
medium:
This has two Mach-Zehnder interferometers coupled with a Kerr medium,
which we shall take to have  . If the input state is
. If the input state is
 , using mode labeling
, using mode labeling  , then the
state after the first two 50/50 beamsplitters is
, then the
state after the first two 50/50 beamsplitters is

up to a normalization factor which we shall suppress for clarity. The
Kerr medium takes  and leaves all other basis
states unchanged. Thus,
and leaves all other basis
states unchanged. Thus,

Finally, the output state, given by applying  to modes
to modes  and
and
 , is
, is

Compare this with the two-mode infinitely squeezed state  which we used in the discussion of teleportation. This state has exactly the same feature that when mode
which we used in the discussion of teleportation. This state has exactly the same feature that when mode  has a single
photon, mode
has a single
photon, mode  does also, and vice versa. The same is true also for
modes
does also, and vice versa. The same is true also for
modes  and
and  . This state has an extra spatial correlation that
the two-mode infinitely squeezed state did not. But is is not hard to
imagine that they have similar properties. In the section on Entangled Photons we
show that both are entangled quantum states, which have
correlations beyond what is possible with classical states.
. This state has an extra spatial correlation that
the two-mode infinitely squeezed state did not. But is is not hard to
imagine that they have similar properties. In the section on Entangled Photons we
show that both are entangled quantum states, which have
correlations beyond what is possible with classical states.
Deutsch-Jozsa algorithm
Nonlinear Mach-Zender interferometers are also useful for implementing
and understanding simple quantum algorithms. One of the most elementary
of these is known as the Deutsch-Jozsa algorithm, which solves the
following problem.
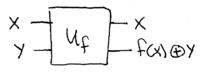
Suppose you are given the following box, which accepts two inputs  and
and  , and produces two outputs,
, and produces two outputs,  and
and  , where
, where
 denotes addition modulo two:
denotes addition modulo two:
Each signal is a single bit, and the box is promised to implement one
of four functions, computing either  ,
,  ,
,  , or
, or  :
:
 |  |  |  | 
|
|
0 | 0 | 0 | 1 | 1
|
|
1 | 0 | 1 | 1 | 0
|
Call  and
and  the even functions, and
the even functions, and  and
and  the
odd functions. How many queries to the box must you perform to
determine whether it is implementing an even or odd function?
the
odd functions. How many queries to the box must you perform to
determine whether it is implementing an even or odd function?
If  and
and  are the only two values you can input for
are the only two values you can input for  and
and  ,
then at least two queries to the box are needed to answer this
question. This can be seen by direct examination of the full
input-output table:
,
then at least two queries to the box are needed to answer this
question. This can be seen by direct examination of the full
input-output table:
 |  |  |  |
 | 
|
|
0 | 0 | 0 | 0 | 1 | 1
|
|
0 | 1 | 0 | 1 | 1 | 0
|
|
1 | 0 | 1 | 1 | 0 | 0
|
|
1 | 1 | 1 | 0 | 0 | 1
|
and by observing that (1) changing  gives no additional information
about whether
gives no additional information
about whether  implements an even or odd function, and (2) for
any single input value of
implements an even or odd function, and (2) for
any single input value of  , there are both even and odd functions
which give the same output. Indeed, whether the function is even or
odd is given by
, there are both even and odd functions
which give the same output. Indeed, whether the function is even or
odd is given by  , and this expression clearly needs
two evaluations of
, and this expression clearly needs
two evaluations of  to be computed, in general.
to be computed, in general.
If quantum superpositions are allowed as inputs, but the outputs are
simply measured in the usual "computational" basis, then the problem
still takes two queries to be solved.
However, if quantum superpositions are allowed as inputs, and outputs
can also be intefered, then only one query is needed. This is
done using the following procedure. Let us use dual-rail photon
qubits, and choose  to represent
to represent  , and
, and  to represent
to represent
 . The optical setup implementing the quantum algorithm to solve
the Deutsch-Jozsa problem is:
. The optical setup implementing the quantum algorithm to solve
the Deutsch-Jozsa problem is:
The key to understanding how this works is to explicitly write down
what is inside the  box for the four possible functions. These
are
box for the four possible functions. These
are
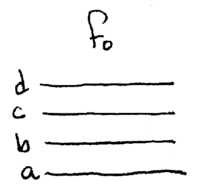
Note how  is trivial, since
is trivial, since  ; also
straighforward is
; also
straighforward is  , since this is just an
inversion of
, since this is just an
inversion of  , that is accomplished by swapping modes
, that is accomplished by swapping modes  and
and  .
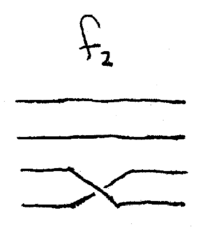
The two odd functions involve an interaction between modes
.
The two odd functions involve an interaction between modes  and
and
 , because
, because  , and
, and  . These two are implemented with nonlinear
Mach-Zehnder interferometers, which cause modes
. These two are implemented with nonlinear
Mach-Zehnder interferometers, which cause modes  and
and  to be
swapped if mode
to be
swapped if mode  has a photon, or left alone if mode
has a photon, or left alone if mode  has no
photon.
has no
photon.
Inserting these into the algorithm, we find that if the input state is
 (designating modes as
(designating modes as  ), the outputs are
), the outputs are
|
function | output state
|
 | 
|
 | 
|
 | 
|
 | 
|
When the function is  or
or  , the
, the  modes completely
decouple from the
modes completely
decouple from the  modes, so the output is trivially obtained.
modes, so the output is trivially obtained.
Thus, for those two cases, modes  end up in
end up in  , so a photon
is found in mode
, so a photon
is found in mode  . When the function is
. When the function is  , then the two
initial beamsplitters on
, then the two
initial beamsplitters on  cancel, leaving a photon in mode
cancel, leaving a photon in mode  .
This photon then causes the nonlinear Mach-Zehnder interferometer in
modes
.
This photon then causes the nonlinear Mach-Zehnder interferometer in
modes  to flip the photons between those modes. A similar thing
happens for function
to flip the photons between those modes. A similar thing
happens for function  , leaving modes
, leaving modes  in state
in state  , so a
photon is found in mode
, so a
photon is found in mode  . The measurement of whether a photon
ends up in mode
. The measurement of whether a photon
ends up in mode  or in mode
or in mode  thus determines whether the
function is even or odd.
thus determines whether the
function is even or odd.
The main insight given by this example, which generalizes to more
complex quantum algorithms, is that phases and interference are
central to their operation. Another important insight is that quantum
algorithms are somewhat of like a kind of spectroscopy: just as the standard
Mach-Zehnder interferometer may be used to measure the index of
refraction of an unknown crystal, nonlinear, coupled Mach-Zehnder
interferometers can be used to measure periods of certain functions.
Indeed, it is through period measurement that Shor's quantum factoring
algorithm works.
Another important insight gained by this example is that quantum
algorithms are likely complex and difficult to implement, if they
require a multitude of coupled interferometers. This is because well
balanced, stable interferometers are experimentally challenging to
realize. Nonlinear optical Kerr media that have no loss, and can
impart a  cross phase modulation between single photons, are also
rather exotic.
cross phase modulation between single photons, are also
rather exotic.
Finally, it is worthwhile considering exactly what we used which was
quantum-mechanical in implementing the Deutsch-Jozsa algorithm. Would
this implementation have worked with coherent states, instead of
single photons?
References














![{\displaystyle B=\exp \left[{\theta \left({a^{\dagger }b-ab^{\dagger }}\right)}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cde964c0c37431a84260835508da295a53bd5290)
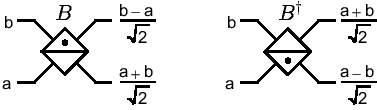









![{\displaystyle C_{1}=[G,C_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f83df0933d6a3c3706b351c36fb81538515a85b9)
![{\displaystyle C_{2}=[G,C_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6157b6fd985b0ff55033671895f6dccd4a5d81)
![{\displaystyle C_{3}=[G,C_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb7b38ae279f6651995a6a493bacfe81b34c5880)

![{\displaystyle C_{n}=[G,C_{n-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9d20f4ef4def8f2300f808179588f8bfdbf739f)
![{\displaystyle [a,a^{\dagger }]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/671da8b1eb59fe1c04e601cc7963a6511d88c74e)
![{\displaystyle [b,b^{\dagger }]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ffc8deb8c5daa77fae70826f05172239777e632)
![{\displaystyle [G,a]=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c839dfe2562400194bd40409990af8c8105a447f)
![{\displaystyle [G,b]=-a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e66ece5d36dd8598163277d2bf53cc526ae88e9)



![{\displaystyle C_{1}=[G,a]=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3abeae2e5e7f5457bbed75f80bbf6ed33383864)
![{\displaystyle C_{2}=[G,C_{1}]=-a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ad248c8f33c48531a9cc5c09f1b481560f63e05)
![{\displaystyle C_{3}=[G,C_{2}]=-[G,C_{0}]=-b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b328c9d224959a15fe187a32c21e8acd51a7ffd0)

















![{\displaystyle B(\theta )\left[{\begin{array}{c}{\alpha }\\{\beta }\end{array}}\right]=\left[{\begin{array}{cc}{\cos \theta }&{-\sin \theta }\\{\sin \theta }&{\cos \theta }\end{array}}\right]\left[{\begin{array}{c}{\alpha }\\{\beta }\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbd7073849d13faa33b118bd924076ccde2ef741)


![{\displaystyle P(\phi )\left[{\begin{array}{c}{\alpha }\\{\beta }\end{array}}\right]=e^{-i\theta /2}\left[{\begin{array}{cc}{e^{i\theta /2}}&{0}\\{0}&{e^{-i\theta /2}}\end{array}}\right]\left[{\begin{array}{c}{\alpha }\\{\beta }\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23b28130466753154f3e728eff05df125e6f33ac)

![{\displaystyle {\begin{array}{rcl}X&=&\left[{\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}}\right]\\Y&=&\left[{\begin{array}{cc}{0}&{-i}\\{i}&{0}\end{array}}\right]\\Z&=&\left[{\begin{array}{cc}{1}&{0}\\{0}&{-1}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f4c4dc132ee998872269c6b90b2cac55933dcdc)
![{\displaystyle {\begin{array}{rcl}B(\theta )&=&\exp \left[{i\theta Y}\right]\\P(\phi )&=&\exp \left[{i\phi Z/2}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed1c798b58ec2107ccfe2fb5b482d0433eb05ea)



![{\displaystyle {\begin{array}{rcl}R_{x}(\theta )&\equiv &e^{-i\theta X/2}=\cos {\frac {\theta }{2}}I-i\sin {\frac {\theta }{2}}X=\left[{\begin{array}{cc}\cos {\frac {\theta }{2}}&-i\sin {\frac {\theta }{2}}\\-i\sin {\frac {\theta }{2}}&\cos {\frac {\theta }{2}}\end{array}}\right]\\R_{y}(\theta )&\equiv &e^{-i\theta Y/2}=\cos {\frac {\theta }{2}}I-i\sin {\frac {\theta }{2}}Y=\left[{\begin{array}{cc}\cos {\frac {\theta }{2}}&-\sin {\frac {\theta }{2}}\\\sin {\frac {\theta }{2}}&\cos {\frac {\theta }{2}}\end{array}}\right]\\R_{z}(\theta )&\equiv &e^{-i\theta Z/2}=\cos {\frac {\theta }{2}}I-i\sin {\frac {\theta }{2}}Z=\left[{\begin{array}{cc}e^{-i\theta /2}&0\\0&e^{i\theta /2}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87225207af366d9d68d1998719ba6d411b5dace3)






![{\displaystyle {\begin{array}{rcl}U=\left[{\begin{array}{cc}e^{i(\alpha -\beta /2-\delta /2)}\cos {\frac {\gamma }{2}}&-e^{i(\alpha -\beta /2+\delta /2)}\sin {\frac {\gamma }{2}}\\e^{i(\alpha +\beta /2-\delta /2)}\sin {\frac {\gamma }{2}}&e^{i(\alpha +\beta /2+\delta /2)}\cos {\frac {\gamma }{2}}\end{array}}\right].\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cdffa723507b330398ac45f72d11c6d7247cbd5)
![{\displaystyle {\begin{array}{rcl}H={\frac {1}{\sqrt {2}}}\left[{\begin{array}{cc}{1}&{1}\\{1}&{-1}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f26d09a9191a1aa422af968868ed8ff0ea03c7)






![{\displaystyle {\begin{array}{rcl}{B}^{\dagger }(\pi /4)P(\phi )B(\pi /4)&=&\exp \left[{-i\pi Y/4}\right]\exp \left[{i\phi Z/2}\right]\exp \left[{i\pi Y/4}\right]\\&=&R_{y}(\pi /2)R_{z}(-\phi )R_{y}(-\pi /2)\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d6da722c294cc51f364863de15b94d011bd159f)

































![{\displaystyle {\begin{array}{rcl}U&=&\exp \left[{i\xi {c}^{\dagger }c\left({\frac {b^{\dagger }-a^{\dagger }}{\sqrt {2}}}\right)\left({\frac {b-a}{\sqrt {2}}}\right)}\right]\\&=&e^{i{\frac {\pi }{2}}{b}^{\dagger }b}\,e^{{\frac {\xi }{2}}{c}^{\dagger }c(a^{\dagger }b-b^{\dagger }a)}\,e^{-i{\frac {\pi }{2}}{b}^{\dagger }b}\,e^{i{\frac {\xi }{2}}{a}^{\dagger }a\,{c}^{\dagger }c}\,e^{i{\frac {\xi }{2}}{b}^{\dagger }b\,{c}^{\dagger }c}\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1ff05608c395719413ce0921bb72fa03bf5b2c)
![{\displaystyle F(\xi )=\exp \left[{{\frac {\xi }{2}}{c}^{\dagger }c\,(a^{\dagger }b-b^{\dagger }a)}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4437ff0a1688cced07348cbd6429a496328cb18)