Difference between revisions of "Atoms"
imported>Ketterle |
imported>Ketterle |
||
| Line 73: | Line 73: | ||
See [[Metrology and Precision Measurement and Units]] | See [[Metrology and Precision Measurement and Units]] | ||
| + | |||
| + | <ul><li> '''CohenT''': Claude Cohen-Tannoudji, Bernard Diu, and Franck Laloë. ''Quantum Mechanics''. Hermann, Paris, 1977. | ||
| + | <li> '''Freeman1976''': Richard R. Freeman and Daniel Kleppner. Core polarization and quantum defects in high-angular-momentum states of alkali atoms. ''Phys. Rev. A'', 14(5):1614–1619, Nov 1976. | ||
| + | <li> '''Gasiorowicz''': Stephen Gasiorowicz. ''Quantum Physics''. Wiley, 2003. | ||
| + | <li> '''Landau''': L. D. Landau and L. M. Lifshitz. ''Quantum Mechanics: Non-Relativistic Theory''. Elsevier Science, 1977. | ||
| + | <li> '''Ludlow2006''': A. D. Ludlow, M. M. Boyd, T. Zelevinsky, S. M. Foreman, S. Blatt, M. Notcutt, T Ido, and J. Ye. Systematic study of the sr-87 clock transition in an optical lattice. ''Physical Review Letters'', 96(3):033003, 2006. | ||
| + | <li> '''Ludlow2008''': A. D. Ludlow, T. Zelevinsky, G. K. Campbell, S. Blatt, M. M. Boyd, M. H. G. de Miranda, M. J. Martin, J. W. Thomsen, S. M. Foreman, Jun Ye, T. M. Fortier, J. E. Stalnaker, S. A. Diddams, Y. Le Coq, Z. W. Barber, N. Poli, N. D. Lemke, K. M. Beck, and C. W. Oates. Sr lattice clock at <math>1\times 10^{-16}</math> fractional uncertainty by remote optical evaluation with a ca clock. ''Science'', page 1153341, 2008. | ||
| + | <li> '''codata2002''': Peter J. Mohr, Barry N. Taylor, and David B. Newell. CODATA recommended values of the fundamental physical constants: 2002. ''Rev. Mod. Phys.'', 77, Jan 2005. Available online at <url> | ||
| + | |||
| + | </url>http://physics.nist.gov/constants. | ||
| + | <li> '''Parsons1967''': R. G. Parsons and V. F. Weisskopf. ''Z. Phys.'', 202:492, 1967. | ||
| + | <li> '''Seaton1966''': M. J. Seaton. ''Proc. Phys. Soc.'', 88:801, 1966. | ||
| + | </ul> | ||
| + | <br style="clear: both" /> | ||
| + | |||
== Notes == | == Notes == | ||
[[Category:8.421]] | [[Category:8.421]] | ||
Revision as of 05:40, 22 February 2010
Contents
- 1 Introduction
- 2 Hydrogen Atom
- 3 References
- 4 Atomic Units
- 5 One-Electron Atoms with Cores
- 6 Spectroscopic Notation
- 7 Energy Levels of Helium
- 8 References
- 9 Appendix: Solution of the Schrodinger Equation
- 10 Appendix: More on the Quantum Defect
- 11 Appendix: Metrology and Precision Measurement and Units
- 12 Notes
Introduction
We could have continued our discussion of two-level systems and resonance and introduced line shapes and various modes of excitation---but first we want to look where the lines come from: from atomic structure. We'll begin by considering the electronic structure in hydrogen and, more generally, atoms with one valence electron, then study the case of helium to understand the effect of adding a second electron. In two subsequent chapters, we will consider the more detailed energy-level structure of hydrogen, including fine structure, the Lamb shift, and effects of the nucleus (hyperfine structure) and of external magnetic and electric fields.
Hydrogen Atom
Bohr's Postulates
We briefly review the Bohr atom-- a model that was soon obsolete, but which nevertheless provided the major impetus for developing quantum mechanics. Balmer's empirical formula of 1885 had reproduced Angstrom's observations of spectral lines in hydrogen to 0.1 Å accuracy, but it was not until 1913 that Bohr gave an explanation for this based on a quantized mechanical model of the atom. This model involved the postulates of the Bohr Atom:
- Electron and proton are point charges whose interaction is coulombic at all distances.
- Electron moves in circular orbit about the center of mass in stationary states with orbital angular momentum .
These two postulates give the energy levels:
- One quantum of radiation is emitted when the system changes between these energy levels.
- The wave number of the radiation is given by the energy difference between the two levels:
Note that the wave number is a spectroscopic unit defined as the number of wavelengths per cm, = . It is important not to confuse the wave number with the magnitude of the wave vector which defines a traveling wave of the form exp. The magnitude of the wave vector is times the wave number.
The mechanical spirit of the Bohr atom was extended by Sommerfeld in 1916 using the Wilson-Sommerfeld quantization rule (valid in the JWKB approximation),
where and are conjugate coordinate and momentum pairs for each degree of freedom of the system. This extension yielded elliptical orbits which were found to have an energy nearly degenerate with respect to the orbital angular momentum for a particular principal quantum number . The degeneracy was lifted by a relativistic correction whose splitting was in agreement with the observed fine structure of hydrogen. (This was a great cruel coincidence in physics. The mechanical description ultimately had to be completely abandoned, in spite of the excellent agreement of theory and experiment.) Although triumphant in hydrogen, simple mechanical models of helium or other two-electron atoms failed, and real progress in understanding atoms had to await the development of quantum mechanics.
Solution of Schrodinger Equation: Key Results
As you will recall from introductory quantum mechanics, the Schrodinger equation
can be solved exactly for the Coulomb Hamiltonian
by separation of variables
Summary of important results
Here, we highlight some important results:
- , just as in the Bohr model
Here, is the Rydberg constant and , where is the effective mass. Note that the relation
follows directly from the Virial Theorem, which states in general that For a spherically symmetric potential of the form , we have and for the special case of the Coulomb potential
(Note: In addition to the important case of the Coulomb potential, it is worth remembering the Virial Theorem for the harmonic oscillator, .)
The same factor of from the Virial Theorem appears in the relationship between the Rydberg constant and the atomic unit of energy, the hartree:
We are working here in cgs units because the expressions are more concise in cgs than in SI. To convert to SI, simply make the replacement .
Probability density of electron wavefunction at origin
Question: How does the density of an -electron at the origin depend on and ?
- A.
- B.
- C.
- D.
The exact result for the density at the origin is (C). To arrive at the scaling, we observe that the and only appear in the Hamiltonian in the combination . Thus, any result for hydrogen can be extended to the case of nuclear charge simply by making the substiution . This leads, in turn, to the substitutions
Thus, the density , so the answer can only be A or C. It is tempting to assume that the scaling can be derived from the length scale . However, the characteristic length for the density at the origin is that which appears in the exponential term of the wavefunction ,
Thus,
for all . Remember this scaling, as it will be important for understanding such effects as the quantum defect in atoms with core electrons and hyperfine structure.
Probability density near origin
For the case of , has a node at , but the density near the origin is nonetheless of interest. It can be shown (Landau III, Chapter 36 .[1]) that, for small ,
Since , the density near the origin scales for large as
References
Atomic Units
The natural units for describing atomic systems are obtained by setting to unity the three fundamental constants that appear in the hydrogen Hamiltonian, . One thus arrives at atomic units, such as
- length: Bohr radius =
- energy: 1 hartree =
- velocity:
- electric field:
- Note: This is the characteristic value for the orbit of hydrogen.
As we see above, we can express atomic units in terms of instead of by introducing a single dimensionless constant
The fine structure constant obtained its name from the appearance of in the ratio of fine structure splitting to the Rydberg; it is the only fundamental constant in atomic physics. As such, it should ultimately be predicted by a complete theory of physics. Whereas precision measurements of other constants are made in atomic physics for purely metrological purposes , , as a dimensionless constant, is not defined by metrology. Rather, characterizes the strength of the electromagnetic interaction, as the following example will illustrate. If energy uncertainties become become as large as , the concept of a particle breaks down. This upper bound on the energy uncertainty gives us, via the Heisenberg Uncertainty Principle, a lower bound on the length scale within which an electron can be localized (before e.g. spontaneous pair production may occur) Even at this short distance of , the Coulumb interaction---while stronger than that in hydrogen at distance --- is only:
i.e. in relativistic units the strength of this "stronger" Coulomb interaction is . The fact that implies that the Coulomb interaction is weak.
One-Electron Atoms with Cores
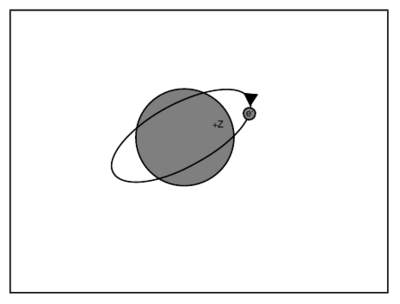
One-electron atom with core of net charge Z.
Question: Consider now an atom with one valence electron of principle quantum number outside a core (comprising the nucleus and filled shells of electrons) of net charge . Which of the following forms describes the lowest order correction to the hydrogenic energy ?
- A.
- B.
- C.
- D.
Both C and D are correct answers, equivalent to lowest order in . This scaling can be derived via perturbation theory. In particular, we can model the atom with a core of net charge as a hydrogenic atom with nuclear charge ---described by Hamiltonian ---and add a perturbing Hamiltonian to account for the penetration of the valence electron into the core. As we showed before, . Thus, for the Hamiltonian
where the penetration correction is localized around , the deviation from hydrogenic energy levels is
where the proportionality constant depends on . In particular, we can define the quantum defect such that
The energy levels then take the form
This accounts for phenomenological formula for term values in the Balmer-Ritz formula,
This formula, in which the are non-integers but are spaced by integer differences, had been deduced spectroscopically long before it could be understood quantum mechanically. See Appendix \ref{app:qdefect} for a derivation of the quantum defect based on solving the radial Schrodinger equation in the JWKB approximation, which sheds light on the relation of the quantum defect to the phase shift of an electron scattering off a modified Coulomb potential; and for a sample calculation of the quantum defect for a model atom.
Spectroscopic Notation
Neutral atoms consist of a heavy nucleus with charge surrounded by electrons. Positively charged atomic ions generally have structure similar to the atom with the same number of electrons except for a scale factor; negative ions lack the attractive Coulomb interaction at large electron-core separation and hence have few if any bound levels. Thus the essential feature of an atom is its number of electrons, and their mutual arrangement as expressed in the quantum numbers. An isolated atom has two good angular momentum quantum numbers, and . (This is strictly true only for atoms whose nuclei have spin . However, is never significantly affected by coupling to in ground state atoms.) In zero external field the atomic Hamiltonian possesses rotational invariance which implies that each level is degenerate with respect to the states with specific (traditional atomic spectroscopists call these states "sublevels"). For each , an atom will typically have a large number of discrete energy levels (plus a continuum) which may be labeled by other quantum numbers. If Russell-Saunders coupling ( coupling) is a good description of the atom (true for light atoms), then and , where
are nearly good quantum numbers and may be used to distinguish the levels. In this case the level is designated by a Term symbolized where and are written numerically and is designated with this letter code:
| : | O | 1 | 2 | 3 | 4 | ... | ||
| Letter: |
The Letters stand for Sharp, Principal, Diffuse, and Fundamental - adjectives applying to the spectral lines of one electron atoms. When describing a hydrogenic atom, the term is preceded by the principle quantum number of the outermost electron. For example, in sodium, the ground state is designated , while the D-line excited states are and . This discussion of the term symbol has been based on quantum numbers for all electrons of the atom. Alternatively one may have or assume knowledge of the internal structure - the quantum numbers of each electron. These are specified as the configuration, e.g..
a product of symbols of the form which represents electrons in the orbital , . is the principal quantum number, which characterizes the radial motion and has the largest influence on the energy. and are written numerically, but the ... coding is used for . Returning to the example of sodium, the configuration is , which is often abbrevated to simply . In classifying levels, the term is generally more important that the configuration because it determines the behavior of an atom when it interacts with or fields. Selection rules, for instance, generally deal with , , . Furthermore the configuration may not be pure - if two configurations give rise to the same term (and have the same parity) then intra-atomic electrostatic interactions can mix them together. This process, called configuration interaction, results in shifts in the level positions and intensities of special lines involving them as well as in correlations in the motions of the electrons within the atoms.
Energy Levels of Helium
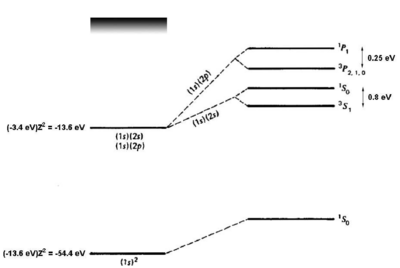
<figure id="he_levels" noautocaption> Figure %i. Energy levels of helium. Figure adapted from Gasiorowicz. [2] The quantum mechanics texts of Gasiorowicz and Cohen-Tannoudji [3] are valuable resources for more detailed treatment of the helium atom. </figure>
If we naively estimate the binding energy of ground-state helium () as twice the binding energy of a a single electron in a hydrogenic atom with , we obtain . Comparing to the experimental result of 79 eV, we see a big (39 eV) discrepancy. However, we have neglected the interaction. Introducing a perturbation operator
where is the distance between the two electrons, and still approximating each electron to be in the state---yielding a total wavefunction ---we obtain the first-order correction
which removes most of the discrepancy. A single-parameter variational ansatz using as parameter removes of the remaining discrepancy. Thus, although we cannot solve the helium Hamiltonian exactly, we can understand the ground-state energy well simply by taking into account the shielding of the nuclear charge by the interaction. For the first excited states, there are two possible electronic configurations, and . The electron sees a shielded nucleus (He vs. He) due to the electron, and consequently has a smaller binding energy, comparable to the binding energy for hydrogen ( eV). For the electron, which has no node at the nucleus, the shielding effect is similar but weaker (see <xr id="he_levels" />). Consider now the possible terms for the configuration:
- (singlet)
- (triplet)
The singlet and triplet states are, respectively, antisymmetric and symmetric under particle exchange. Since Fermi statistics demand that the total wavefunction of the electrons be antisymmetric, the spatial and spin wavefunctions must have opposite symmetry,
Here, is the wavefunction with symmetric spatial part and antisymmetric spin state , i.e. the spin singlet (S=0, term). is the wavefunction with antisymmetric spatial part and symmetric spin state , i.e. the spin triplet (S=1, term). Now consider the Coulomb energy of the interaction in these excited states:
The first term (called the Coulomb term, although both terms are Coulombic in origin) is precisely what we would calculate classically for the repulsion between two electron clouds of densities and . The second term, the exchange term, is a purely quantum mechanical effect associated with the Pauli exclusion principle. The triplet state has lower energy, because the antisymmetric spatial wavefuntion reduces repulsion interactions. Since the interaction energy is spin-dependent, it can be written in the same form as a ferromagnetic spin-spin interaction,
<equation id="ferro" noautocaption> (%i)
</equation> To see this, we use the relation . Since , <xr id="ferro"/> is equivalent to
where we have substituted for the singlet and triplet states, respectively. Bear in mind that, although the interaction energy is spin-dependent, the origin of the coupling is electrostatic and not magnetic. Because of its electrostatic origin, the exchange energy (0.8 eV for the splitting, as indicated in <xr id="he_levels" />) is much larger than a magnetic effect such as the fine structure splitting, which carries an extra factor of .
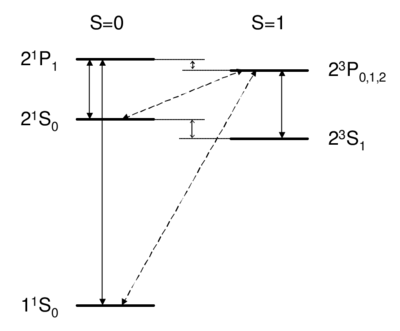
Dipole-allowed transitions (solid) and intercombination lines (dashed) in helium.
What field (coupling) drives singlet-triplet transitions?
A. Optical fields (dipole operator)
B. rotating magnetic fields
C. Both
D. None
Singlet-triplet transitions are forbidden by the selection rule, so to first order the answer is D. A is ruled out because the dipole operator acts on the spatial wavefunction, not on the spin part. One might think (B) that a transverse magnetic field, which couples to , , , can be used to flip a spin. However, a transverse field can only rotate the two spins together; it cannot rotate one spin relative to the other, as would be necessary to change the magnitude of . Because all spin operators are symmetric against particle exchange, they couple only . Thus, spatial and spin symmetry (S,A) are both good quantum numbers. More formally, all observables commute with the particle exchange operator , and (S or A) is a good quantum number. Thus, as long as wavefunction and operators separate into spin dependent and space dependent parts , both 's are conserved. Intercombination (i.e. transition between singlet and triplet) is only possible when this assumption is violated, i.e. when the spin and spatial wavefunctions are mixed, e.g. by spin orbit coupling. As we will see later on, spin orbit coupling is , and hence is weak for helium. Thus, the state of helium is very long-lived, with a lifetime of about 8,000 s. Historically, the absence of transition between singlet and triplet states led to the belief that there were two kinds of helium, ortho-helium (triplet) and para-helium (singlet).
The other noble gases (Ne, Ar, Kr, Xe) have lifetimes on the order of 40 s. Because they are so narrow, intercombination lines are of great interest for application in optical clocks. While a lifetime of 8000 s is too long to be useful (because such a narrow transition is difficult both to find and to drive), intercombination lines in Mg, Ca, or Sr---with linewidths ranging from mHz to kHz---are discussed as potential optical frequency standards. [4] [5]
How can you measure an 8000 s lifetime? Well, definitely not by observing the decay of the excited state over 8000 s since collisions and other effects will shorten the lifetime. However, if you measure the rate of emitted XUV photons and the number of atoms in the emitting state, you get the lifetime. Absolute measurements of these numbers are difficult, and therefore the accuracy for the lifetime will not be high. A very elegant method has been recently applied to metastable helium.[6] While recording the XUV photon rate, the atoms in the state are strongly driven to the state, saturating the transition, putting half of the atoms into the state which has a known (and more easily measured) lifetime of 5.7 ms. The XUV rate jumps up by a factor of about a million which is half the ratio of the lifetimes of the two states.
References
Appendix: Solution of the Schrodinger Equation
See Solution of the Schrodinger Equation for an Atom
Appendix: More on the Quantum Defect
See More on the Quantum Defect
Appendix: Metrology and Precision Measurement and Units
See Metrology and Precision Measurement and Units
- CohenT: Claude Cohen-Tannoudji, Bernard Diu, and Franck Laloë. Quantum Mechanics. Hermann, Paris, 1977.
- Freeman1976: Richard R. Freeman and Daniel Kleppner. Core polarization and quantum defects in high-angular-momentum states of alkali atoms. Phys. Rev. A, 14(5):1614–1619, Nov 1976.
- Gasiorowicz: Stephen Gasiorowicz. Quantum Physics. Wiley, 2003.
- Landau: L. D. Landau and L. M. Lifshitz. Quantum Mechanics: Non-Relativistic Theory. Elsevier Science, 1977.
- Ludlow2006: A. D. Ludlow, M. M. Boyd, T. Zelevinsky, S. M. Foreman, S. Blatt, M. Notcutt, T Ido, and J. Ye. Systematic study of the sr-87 clock transition in an optical lattice. Physical Review Letters, 96(3):033003, 2006.
- Ludlow2008: A. D. Ludlow, T. Zelevinsky, G. K. Campbell, S. Blatt, M. M. Boyd, M. H. G. de Miranda, M. J. Martin, J. W. Thomsen, S. M. Foreman, Jun Ye, T. M. Fortier, J. E. Stalnaker, S. A. Diddams, Y. Le Coq, Z. W. Barber, N. Poli, N. D. Lemke, K. M. Beck, and C. W. Oates. Sr lattice clock at fractional uncertainty by remote optical evaluation with a ca clock. Science, page 1153341, 2008.
- codata2002: Peter J. Mohr, Barry N. Taylor, and David B. Newell. CODATA recommended values of the fundamental physical constants: 2002. Rev. Mod. Phys., 77, Jan 2005. Available online at <url> </url>http://physics.nist.gov/constants.
- Parsons1967: R. G. Parsons and V. F. Weisskopf. Z. Phys., 202:492, 1967.
- Seaton1966: M. J. Seaton. Proc. Phys. Soc., 88:801, 1966.
Notes
- ↑ Landau: L. D. Landau and L. M. Lifshitz. Quantum Mechanics: Non-Relativistic Theory. Elsevier Science, 1977
- ↑ Stephen Gasiorowicz. Quantum Physics. Wiley, 2003
- ↑ Claude Cohen-Tannoudji, Bernard Diu, and Franck Laloë. Quantum Mechanics. Hermann, Paris, 1977
- ↑ A. D. Ludlow, T. Zelevinsky, G. K. Campbell, S. Blatt, M. M. Boyd, M. H. G. de Miranda, M. J. Martin, J. W. Thomsen, S. M. Foreman, Jun Ye, T. M. Fortier, J. E. Stalnaker, S. A. Diddams, Y. Le Coq, Z. W. Barber, N. Poli, N. D. Lemke, K. M. Beck, and C. W. Oates. Sr lattice clock at 1×10−16 fractional uncertainty by remote optical evaluation with a ca clock. Science, page 1153341, 2008.
- ↑ A. D. Ludlow, M. M. Boyd, T. Zelevinsky, S. M. Foreman, S. Blatt, M. Notcutt, T Ido, and J. Ye. Systematic study of the sr-87 clock transition in an optical lattice. Physical Review Letters, 96(3):033003, 2006.
- ↑ S.S. Hodgman, R.G. Dall, L.J. Byron, K.G.H. Baldwin, S.J. Buckman, and A.G. Truscott. Phys. Rev. Lett., 103:053002, 2009.
















![{\displaystyle \langle r_{n\ell }\rangle ={\frac {n^{2}a_{0}}{Z}}\{1+{\frac {1}{2}}[1-{\frac {\ell (\ell +1)}{n^{2}}}]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20007b307fe177b643a0543125ed8e7e90ff24e1)



































































































































![{\displaystyle {\begin{aligned}\Delta E&={\frac {1}{2}}\int \int {\frac {e^{2}}{r_{12}}}[|\psi _{100}(r_{1})|^{2}|\psi _{200}(r_{2})|^{2}+(r_{1}\leftrightarrow r_{2})]\\&\pm {\frac {1}{2}}\int \int {\frac {e^{2}}{r_{12}}}[\psi _{100}^{*}(r_{1})\psi _{200}^{*}(r_{2})\psi _{100}(r_{2})\psi _{200}(r_{1})+(r_{1}\leftrightarrow r_{2})]\\&=\Delta E^{Coul}\pm \Delta E^{exch}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f7da0a65ae741e23636787881de55fc50acbe4a)















![{\displaystyle [P_{ij},{\hat {O}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d769b158d5a631785fbe3e4a49023eeb2ea0cabd)





