imported>Wikibot |
imported>Idimitro |
| (38 intermediate revisions by 5 users not shown) |
| Line 1: |
Line 1: |
| − | = Atoms =
| |
| | == Introduction == | | == Introduction == |
| − | We could have continued our discussion of two-level systems and resonance and introduced line shapes and various modes of excitation---but | + | |
| − | first we want to look where the lines come from: from atomic structure. We'll begin by considering the electronic structure in hydrogen and, more generally, atoms with one valence electron, then study the case of helium to understand the effect of adding a second electron. In two subsequent chapters, we will consider the more detailed energy-level structure of hydrogen, including fine structure, the Lamb shift, and effects of the nucleus (hyperfine structure) and of external magnetic and electric fields. | + | <categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;" hideprefix=auto>8.421</categorytree> |
| − | == Hydrogen Atom ==
| + | |
| − | === Bohr's Postulates ===
| + | We could have continued our discussion of two-level systems and |
| − | We briefly review the Bohr atom-- a model that was soon obsolete, but which
| + | resonance and introduced line shapes and various modes of |
| − | nevertheless provided the major impetus for developing quantum
| + | excitation---but first we want to look where the lines come from: from |
| − | mechanics. Balmer's empirical formula of 1885 had reproduced Angstrom's
| + | atomic structure. We'll begin by considering the electronic structure |
| − | observations of spectral lines in hydrogen to 0.1 \AA accuracy,
| + | in hydrogen and, more generally, atoms with one valence electron, then |
| − | but it was not until 1913 that Bohr gave an explanation for this
| + | study the case of helium to understand the effect of adding a second |
| − | based on a quantized mechanical model of the atom. This model
| + | electron. In two subsequent chapters, we will consider the more |
| − | involved the postulates of the Bohr Atom:
| + | detailed energy-level structure of hydrogen, including fine structure, |
| − | \begin{itemize}
| + | the Lamb shift, and effects of the nucleus (hyperfine structure) and |
| − | * Electron and proton are point charges whose interaction is
| + | of external magnetic and electric fields. |
| − | coulombic at all distances.
| + | |
| − | * Electron moves in circular orbit about the center of mass in
| + | The hydrogen atom has played a special role in physics. Dan Kleppner eloquently describes this role in a |
| − | {\it stationary states} with orbital angular momentum <math>L=n\hbar</math>.
| + | [https://cua-admin.mit.edu/apwiki/wiki/images/3/39/Yin_and_Yang_of_Hydrogen_Dan_Kleppner.pdf column in Physics Today] |
| − | \end{itemize}
| + | which starts with the sentence "To understand hydrogen is to understand all of physics". In this section we will unravel a lot of physics using the hydrogen atom - but we also include the helium atom to introduce new phenomena related to the presence of two electrons. |
| − | These two postulates give the energy levels:
| + | |
| − | \\
| + | {{:The Hydrogen Atom}} |
| − | :<math>
| + | |
| − | E_n=-\frac{\overbrace{\overbrace{\left(\frac{1}{2}\frac{me^4}{\hbar^2}\right.}^{R_{\infty}}\overbrace{\left.\frac{M}{M+m}\right)}^{\textrm{reduced
| + | {{:Atomic_Units}} |
| − | mass factor}}}^{R_H}}{n^2}.
| + | |
| − | </math>
| + | {{:One-Electron Atoms with Cores}} |
| − | \begin{itemize}
| + | |
| − | * One quantum of radiation is emitted when the system changes
| + | {{:Spectroscopic_Notation}} |
| − | between these energy levels.
| + | |
| − | * The wave number of the radiation is given by the Bohr frequency
| + | {{:Energy Levels of Helium}} |
| − | criterion\footnote{Note that the wave number is a spectroscopic unit defined as the number
| + | |
| − | of wavelengths per cm,
| + | == Appendix: Solution of the Schrodinger Equation == |
| − | <math>\sigma</math> = <math>1/\lambda</math>. It is important not to confuse the wave number with
| + | |
| − | the magnitude of the wave vector <math>\bf{ k}</math> which defines a traveling wave
| + | See [[Solution of the Schrodinger Equation for an Atom]] |
| − | of the form exp<math>i(k \cdot r -\omega t)</math>. The magnitude of the wave vector is
| + | |
| − | <math>2 \pi</math> times the wave number.}:
| |
| − | \[
| |
| − | \sigma_{n\rightarrow m} = (E_n-E_m)/(hc)
| |
| − | \]
| |
| − | \end{itemize}
| |
| − | The mechanical spirit of the Bohr atom was extended by Sommerfeld
| |
| − | in 1916 using the Wilson-Sommerfeld quantization rule (valid in the JWKB approximation), | |
| − | :<math>
| |
| − | \oint p_i dq_i = n_i h
| |
| − | </math>
| |
| − | where <math>q_i</math> and <math>p_i</math> are conjugate coordinate and momentum pairs
| |
| − | for each degree of freedom of the system. This extension yielded
| |
| − | elliptical orbits which were found to have an energy nearly
| |
| − | degenerate with respect to the orbital angular momentum for a
| |
| − | particular principal quantum number <math>n</math>. The degeneracy was
| |
| − | lifted by a relativistic correction whose splitting was in
| |
| − | agreement with the observed fine structure of hydrogen. (This was a great
| |
| − | cruel coincidence in physics. The mechanical description ultimately
| |
| − | had to be completely abandoned, in spite of the excellent agreement of theory
| |
| − | and experiment.) Although triumphant in hydrogen, simple mechanical models of helium or other two-electron
| |
| − | atoms failed, and real progress in understanding atoms
| |
| − | had to await the development of quantum mechanics.
| |
| − | === Solution of Schr\"{o}dinger Equation: Key Results ===
| |
| − | As you will recall from introductory quantum mechanics, the Schr\"{o}dinger equation
| |
| − | :<math>
| |
| − | i\hbar \frac{d\psi}{dt}=H\psi
| |
| − | </math>
| |
| − | can be solved exactly for the Coulomb Hamiltonian
| |
| − | :<math>
| |
| − | H = -\frac{\hbar^2}{2m}\nabla^2 - \frac{Z e^2}{r}
| |
| − | </math>
| |
| − | by separation of variables
| |
| − | :<math>
| |
| − | \psi_{n\ell m}=R_{n\ell}(r)Y_{\ell m}(\theta,\phi).
| |
| − | </math>
| |
| − | The full solution is reviewed in Appendix \ref{app:schr}. Here, we will highlight some important results:
| |
| − | \begin{itemize}
| |
| − | \item<math>E_n=-R_H\frac{Z^2}{n^2}</math>, just as in the Bohr model
| |
| − | * <math>\langle r_{n\ell}\rangle =\frac{n^2a_0}{Z}\{1+\frac{1}{2}[1-\frac{\ell(\ell+1)}{n^2}]\}</math>
| |
| − | \item<math>\langle \frac{1}{r_{n\ell}}\rangle =\frac{Z}{n^2a_0}</math>
| |
| − | \end{itemize}
| |
| − | Here, <math>R_H=\frac{1}{2}\frac{\mu e^4}{\hbar^2}</math> is the Rydberg constant and <math>a_0=\frac{\hbar^2}{\mu e^2}</math>, where <math>\mu=\frac{m M}{m+M}</math> is the effective mass.
| |
| − | Note that the relation
| |
| − | :<math> | |
| − | E_n=-e^2\langle\frac{1}{r_{n\ell}}\rangle\cdot\frac{1}{2}
| |
| − | </math>
| |
| − | follows directly from the Virial Theorem, which states in general that <math>2\langle T\rangle=\langle x\frac{dV}{dx}\rangle,</math>
| |
| − | so that for a spherically symmetric potential of the form <math>V=r^n</math>, we have <math>\langle T\rangle=\frac{n}{2}\langle V\rangle,</math>
| |
| − | and for the special case of the Coulomb potential (footnote: In addition to the important case of the Coulomb potential, it is worth remembering the Virial Theorem for the harmonic oscillator, <math>n=2\Rightarrow\langle T\rangle=\langle V\rangle</math>.)
| |
| − | :<math>
| |
| − | T=-\frac{1}{2}V.
| |
| − | </math>
| |
| − | The same factor of <math>\frac{1}{2}</math> from the Virial Theorem appears in the relationship between the Rydberg constant and the atomic unit of energy, the hartree:
| |
| − | :<math>
| |
| − | R_H=\frac{e^2}{a_0} \frac{1}{2}=\underbrace{\frac{\mu e^4}{\hbar^2}}_{\textrm{Hartree}}
| |
| − | \frac{1}{2}.
| |
| − | </math>
| |
| − | We are working here in cgs units because the expressions are more concise in cgs than in SI. To convert to SI, simply make the replacement <math>e^2\rightarrow\frac{e^2}{4\pi\varepsilon_0}</math>.
| |
| − | \QA{
| |
| − | How does the density <math>|\psi_{n00}(0)|^2</math> of an <math>s</math>-electron at the origin depend on <math>n</math> and <math>Z</math>?
| |
| − | A. <math>\frac{Z^3}{a_0^3n^6}</math>
| |
| − | B. <math>\frac{Z}{a_0^3n^2}</math>
| |
| − | C. <math>\frac{Z^3}{a_0^3n^3}</math>
| |
| − | D. <math>\frac{Z^2}{a_0^3n^3}</math>
| |
| − | }{
| |
| − | The exact result for the density at the origin is <math>|\psi_{n00}(0)|^2=\frac{Z^3}{\pi a_0^3n^3}</math> (C). To arrive at the <math>Z</math> scaling, we observe that the <math>Z</math> and <math>e</math> only appear in the Hamiltonian (\ref{eq:coulomb}) in the combination <math>Ze^2</math>. Thus, any result for hydrogen can be extended to the case of nuclear charge <math>Z</math> simply by making the substiution <math>e^2\rightarrow Z e^2</math>. This leads, in turn, to the substitutions
| |
| − | :<math>
| |
| − | \begin{split}
| |
| − | a_0 &=\frac{\hbar^2}{me^2}\rightarrow \frac{a_0}{Z}\\
| |
| − | R_\infty &=\frac{me^4}{\hbar^2}\rightarrow Z^2 R_\infty
| |
| − | \end{split}
| |
| − | </math>
| |
| − | Thus, the density <math>|\psi_{n00}(0)|^2\propto a_0^{-3}\propto Z^3</math>, so the answer can only be A or C.
| |
| − | It is tempting to assume that the <math>n</math> scaling can be derived from the length scale <math>\langle\frac{1}{r_{n\ell}}\rangle=\frac{Z}{a_0n^2}</math>. However, the characteristic length <math>l</math> for the density at the origin is that which appears in the exponential term of the wavefunction <math>\psi_{n00}\propto e^{-r/l}</math>,
| |
| − | :<math>
| |
| − | l=na_0/Z.
| |
| − | </math>
| |
| − | Thus,
| |
| − | :<math>
| |
| − | |\psi_{n00}(0)|^2\propto\frac{Z^3}{n^3a_0^3}
| |
| − | </math>
| |
| − | for all <math>n</math>. Remember this scaling, as it will be important for understanding such effects as the quantum defect in atoms with core electrons and hyperfine structure.
| |
| − | }
| |
| − | For the case of <math>\ell\neq0</math>, <math>\psi\propto r^\ell</math> has a node at <math>r=0</math>, but the density \textit{near} the origin is nonetheless of interest. It can be shown (Landau III, \S 36 \cite{Landau}) that, for small <math>r</math>,
| |
| − | :<math>
| |
| − | R_{n\ell}(r) \simeq
| |
| − | r^{\ell}\frac{2^{\ell+1}}{n^{2+\ell}(2\ell+1)!}\sqrt{\frac{(n+\ell)!}{(n-\ell-1)!}}.
| |
| − | </math>
| |
| − | Since <math>\sqrt{\frac{(n+\ell)!}{(n-\ell-1)!}}\overrightarrow{_{n\rightarrow\infty}}\sqrt{n^{2\ell+1}}</math>, the density near the origin scales for large <math>n</math> as
| |
| − | :<math>
| |
| − | |\psi |^2\propto r^{2\ell} \times \frac{1}{n^3}.
| |
| − | </math>
| |
| − | == Atomic Units ==
| |
| − | The natural units for describing atomic systems are obtained by setting to unity
| |
| − | the three fundamental constants that appear in the hydrogen Hamiltonian (Eq.
| |
| − | \ref{eq:coulomb}), <math>\hbar=m=e=1</math>. One thus arrives at atomic units, such as
| |
| − | \begin{itemize}
| |
| − | * length: Bohr radius =
| |
| − | <math>a_0=\frac{\hbar^2}{me^2}=\frac{1}{\alpha}\frac{\hbar}{mc}=0.53\text{\AA}</math>
| |
| − | * energy: 1 hartree = <math>\frac{e^4 m}{\hbar^2}=(\frac{e^2}{c\hbar})^2mc^2=\alpha^2 mc^2=27.2\ \textrm{eV}</math>
| |
| − | * velocity: <math>m v^2=\frac{e^{4}m}{\hbar^2}\Rightarrow v=\frac{e^2}{\hbar}=\alpha\cdot
| |
| − | c=2.2\times 10^8\ \textrm{cm/s}</math>
| |
| − | * electric field: (footnote: This is the characteristic value for the <math>n=1</math> orbit of hydrogen.} <math>\frac{e}{a_0^2}=5.142\times 10^9\ \textrm{V/cm) </math>
| |
| − | \end{itemize}
| |
| − | As we see above, we can express the atomic units in terms of <math>c</math> instead of <math>e</math> by introducing a single dimensionless constant
| |
| − | :<math>
| |
| − | \alpha=\frac{e^2}{\hbar c}\approx\frac{1}{137}.
| |
| − | </math>
| |
| − | The \textit{fine structure constant} (footnote: The name "fine structure constant" derives from the appearance of <math>\alpha^2</math> in the ratio of fine structure splitting to the Rydberg.} <math>\alpha</math> is the only fundamental constant in atomic physics. As such, it should ultimately be predicted by a complete theory of physics. Whereas precision measurements of other constants are made in atomic physics for purely metrological purposes (see Appendix \ref{app:metrology) ), <math>\alpha</math>, as a dimensionless constant, is not defined by metrology. Rather, <math>\alpha</math> characterizes the strength of the electromagnetic interaction, as the following example will illustrate.
| |
| − | If energy uncertainties become become as large as <math>\Delta E=mc^2</math>, the concept of a particle breaks down. This upper bound on the energy uncertainty gives us, via the Heisenberg Uncertainty Principle, a lower bound on the length scale within which an electron can be localized:
| |
| − | <math>\Delta\simeq mc^2\Rightarrow \Delta p=mc</math>
| |
| − | <math>\Delta x=\frac{\hbar}{mc}=\lambda_c</math>
| |
| − | Even at this short distance of <math>\lambda_c</math>, the Coulumb interaction---while stronger than that in hydrogen at distance <math>a_0</math>---is only:<math><math>E_c=\frac{e^2}{\lambda_c}=\frac{e^2mc}{\hbar}=\frac{e^2}{\hbar c}mc^2=\alpha mc^2,</math></math> i.e. in relativistic units the strength of this "stronger" Coulomb interaction is <math>\alpha</math>. That <math>\alpha=\frac{1}{137}</math> says that the Coulomb interaction is weak.
| |
| − | == One-Electron Atoms with Cores ==
| |
| − | \begin{figure}
| |
| − | <blockquote>
| |
| − | ::[[Image:atoms-atom_with_core|thumb|200px|none|]]
| |
| − | (caption: One-electron atom with core of net charge Z.)
| |
| − | </blockquote>
| |
| − | \end{figure}
| |
| − | \QA{ Consider now an atom with one valence electron of principle quantum number <math>n</math> outside a core (comprising the nucleus and filled shells of electrons) of net charge <math>Z</math>. Which of the following forms describes the lowest order correction to the hydrogenic energy <math>E_n=\frac{Z^2R}{n^2}</math>?
| |
| − | A. <math>\frac{Z^2R}{n^2}+\delta</math>
| |
| − | B. <math>\frac{Z^2R}{n^2}+\frac{\delta}{n^2}</math>
| |
| − | C. <math>\frac{Z^2R}{n^2}+\frac{\delta}{n^3}</math>
| |
| − | D. <math>\frac{Z^2R}{(n-\delta)^2}</math>
| |
| − | }{
| |
| − | Both C and D are correct answers, equivalent to lowest order in <math>\delta</math>. This scaling can be derived via perturbation theory. In particular, we can model the atom with a core of net charge <math>Z</math> as a hydrogenic atom with nuclear charge <math>Z</math>---described by Hamiltonian <math>H_0</math>---and add a perturbing Hamiltonian <math>H'</math> to account for the penetration of the valence electron into the core.
| |
| − | As we showed in \ref{q:nZ}, <math>\psi_{n\ell}(r)\overrightarrow{_{r\rightarrow0}}r^{\ell}n^{-\frac{3}{2}}</math>. Thus, for the Hamiltonian
| |
| − | :<math>
| |
| − | H=H_0+H',
| |
| − | </math>
| |
| − | where the penetration correction <math>H'</math> is localized around <math>r=0</math>, the deviation from hydrogenic energy levels <math>E_n</math> is
| |
| − | :<math>
| |
| − | \Delta E_n=\langle\psi_{n\ell}|H'|\psi_{n\ell}\rangle \propto \frac{1}{n^3},
| |
| − | </math>
| |
| − | where the proportionality constant depends on <math>\ell</math>. In particular, we can define the \textit{quantum defect} <math>\delta_\ell</math> such that
| |
| − | :<math>
| |
| − | \Delta E_n=\frac{\delta_\ell}{n^3}2R.
| |
| − | </math>
| |
| − | The energy levels then take the form
| |
| − | :<math>
| |
| − | -E_n=\frac{R}{n^2}+\frac{2R}{n^3}\times\delta_{\ell}\simeq\frac{R}{(n-\delta_{\ell})^2}.
| |
| − | </math>
| |
| − | }
| |
| − | This accounts for phenomenological formula for term values in the Balmer-Ritz formula,
| |
| − | :<math>
| |
| − | T_n=\frac{Z^2R}{n*^2}.
| |
| − |
| |
| − | </math>
| |
| − | This formula, in which the <math>n*</math> are non-integers but are spaced by integer differences, had been deduced spectroscopically long before it could be understood quantum mechanically.
| |
| − | See Appendix \ref{app:qdefect} for a derivation of the quantum defect based on solving the radial Schr\"{o}dinger equation in the JWKB approximation, which sheds light on the relation of the quantum defect to the phase shift of an electron scattering off a modified Coulomb potential; and for a sample calculation of the quantum defect for a model atom.
| |
| − | == Spectroscopic Notation ==
| |
| − |
| |
| − | Neutral atoms consist of a heavy nucleus with charge <math>Z</math>
| |
| − | surrounded by <math>Z</math> electrons. Positively charged atomic ions
| |
| − | generally have structure similar to the atom with the same number
| |
| − | of electrons except for a scale factor; negative ions lack the
| |
| − | attractive Coulomb interaction at large electron-core separation
| |
| − | and hence have few if any bound levels. Thus the essential
| |
| − | feature of an atom is its number of electrons, and their mutual
| |
| − | arrangement as expressed in the quantum
| |
| − | numbers.
| |
| − | An isolated atom has two good angular momentum quantum numbers,
| |
| − | <math>J</math> and <math>M_J</math>. (This is strictly true only for atoms whose nuclei
| |
| − | have spin <math>I = 0</math>. However, <math>J</math> is never significantly destroyed
| |
| − | by coupling to <math>I</math> in ground state atoms.) In zero external field
| |
| − | the atomic Hamiltonian possesses rotational invariance which
| |
| − | implies that each <math>J</math> level is degenerate with respect to the <math>2J
| |
| − | + 1</math> states with specific <math>M_J</math> (traditional atomic
| |
| − | spectroscopists call these states "sublevels"). For each
| |
| − | <math>J</math>,<math>M_J</math> an atom will typically have a large number of discrete
| |
| − | energy levels (plus a continuum) which may be
| |
| − | labeled by other quantum numbers.
| |
| − | If Russell-Saunders coupling (<math>L-S</math> coupling) is a good description of the atom (true for light atoms), then <math>L</math> and <math>S</math>, where
| |
| − | :<math>
| |
| − | L = \sum_{i=1}^{N}{\mathbf { \ell}}_i
| |
| − | </math>
| |
| − | :<math>
| |
| − | S = \sum_{i=1}^{N}S_i
| |
| − | </math>
| |
| − | are nearly good quantum numbers and may be used to distinguish the
| |
| − | levels. In this case the level is designated by a {\it Term}
| |
| − | symbolized <math>^{2S+1}L_J</math> where <math>2S+1</math> and <math>J</math> are written
| |
| − | numerically and <math>L</math>
| |
| − | is designated with this letter code:
| |
| − | <table border=1>
| |
| − | <tr><td>
| |
| − | </td><td></td><td><math>L</math>:</td><td>O</td><td>1</td><td>2</td><td>3</td><td>4</td><td> ...\cr </td><td></td><td>Letter:</td><td><math>S</math></td><td><math>P</math></td><td><math>D</math></td><td><math>F</math></td><td><math>G</math>\cr
| |
| − | </table>
| |
| − | The Letters stand for Sharp, Principal, Diffuse, and Fundamental -
| |
| − | adjectives applying to the spectral lines of one electron atoms.
| |
| − | When describing a hydrogenic atom, the term is preceded by the principle quantum number of the
| |
| − | outermost electron. For example, in sodium, the ground state is designated <math>3^2S_{1/2}</math>, while the D-line excited states are <math>3^2P_{1/2,3/2}</math>.
| |
| − | This discussion of the term symbol has been based on an
| |
| − | external view of the atom. Alternatively one may have or assume
| |
| − | knowledge of the internal structure - the quantum numbers of each
| |
| − | electron. These are specified as the {\it configuration}, e.g..
| |
| − | :<math>
| |
| − | 1s^2 2s^2 2p^2 ,
| |
| − | </math>
| |
| − | a product of symbols of the form <math>n\ell^k</math> which represents <math>k</math>
| |
| − | electrons in the orbital <math>n</math>, <math>\ell</math>. <math>n</math> is the principal
| |
| − | quantum number, which characterizes the radial motion and has the
| |
| − | largest influence on the energy. <math>n</math> and <math>m</math> are written
| |
| − | numerically, but the <math>spdf</math> ... coding is used for <math>\ell</math>. Returning to the example of sodium, the configuration is
| |
| − | <math>1s^2 2s^2 2p^6 3s</math>, which is often abbrevated to simply <math>3s</math>.
| |
| − | In classifying levels, the term is generally more important
| |
| − | that the configuration because it determines the behavior of an
| |
| − | atom when it interacts with <math>E</math> or <math>B</math> fields. Selection
| |
| − | rules, for instance, generally deal with <math>\Delta J, \Delta L, \Delta S</math>. Furthermore the
| |
| − | configuration may not be pure - if two configurations give rise
| |
| − | to the same term (and have the same parity) then intra-atomic
| |
| − | electrostatic interactions can mix them together. This process,
| |
| − | called configuration interaction, results in shifts in the level
| |
| − | positions and intensities of special lines involving them as well
| |
| − | as in correlations in the motions of the electrons within the
| |
| − | atoms.
| |
| − | == Energy Levels of Helium ==
| |
| − | \begin{figure}
| |
| − | <blockquote>
| |
| − | ::[[Image:atoms-helium_levels|thumb|200px|none|]]
| |
| − | (caption: Energy levels of helium. Figure adapted from Gasiorowicz \cite{Gasiorowicz}. The quantum mechanics texts of Gasiorowicz and Cohen-Tannoudji \cite{CohenT} are valuable resources for more detailed treatment of the helium atom.)
| |
| − | </blockquote>
| |
| − | \end{figure}
| |
| − | If we naively estimate the binding energy of ground-state helium (<math>1s^2</math>) as twice the binding energy of a a single electron in a hydrogenic atom with <math>Z=2</math>, we obtain <math>2(Z^2)(13.6 eV)=108\textrm\ {eV}</math>. Comparing to the experimental result of 79 eV, we see a \textit{big} (39 eV) discrepancy. However, we have neglected the <math>e^--e^-</math> interaction. Introducing a perturbation operator
| |
| − | :<math>
| |
| − | V'=\frac{e^2}{r_{12}},
| |
| − | </math>
| |
| − | where <math>r_{12}</math> is the distance between the two electrons, and still approximating each electron to be in the <math>1s</math> state---yielding a total wavefunction <math>\psi_G=\psi_{100}(1)\cdot\psi_{100}(2)</math>---we obtain the first-order correction
| |
| − | :<math>
| |
| − | \Delta E=\langle\psi_G|V'|\psi_G\rangle=34\ \textrm{eV},
| |
| − | </math>
| |
| − | which removes most of the discrepancy. A single-parameter variational ansatz using <math>Z^*</math> as parameter removes <math>\frac{2}{3}</math> of the remaining discrepancy. Thus, although we cannot solve the helium Hamiltonian exactly, we can understand the ground -state energy well simply by taking into account the shielding of the nuclear charge by the <math>e^--e^-</math> interaction.
| |
| − | For the first excited states, there are two possible electronic configurations, <math>1s2s</math> and <math>1s2p</math>. The <math>2p</math> electron sees a shielded nucleus (<math>He^+</math> vs. <math>He^{++}</math>) due to the <math>1s</math> electron, and consequently has a smaller binding energy, comparable to the <math>2p</math> binding energy for hydrogen (<math>\approx 4</math> eV). For the <math>2s</math> electron, which has no node at the nucleus, the shielding effect is similar but weaker (see figure \ref{fig:he_levels}). Consider now the possible terms for the <math>1s2s</math> configuration:
| |
| − | \begin{itemize}
| |
| − | * <math>^1S_0</math> (singlet)
| |
| − | * <math>^3S_1</math> (triplet)
| |
| − | \end{itemize}
| |
| − | The singlet and triplet states are, respectively, antisymmetric and symmetric under particle exchange. Since Fermi statistics demand that the total wavefunction of the electrons be antisymmetric, the spatial and spin wavefunctions must have opposite symmetry,
| |
| − | :<math>
| |
| − | \psi_{S,A}=\frac{1}{\sqrt{2}}\left(\psi_{100}(r_1)\psi_{200}(r_2)\pm\psi_{100}(r_2)\psi_{200}(r_1)\right)\chi_{A,S}.
| |
| − | </math>
| |
| − | Here, <math>\psi_S</math> is the wavefunction with symmetric spatial part and antisymmetric spin state <math>\chi_A</math>, i.e. the spin singlet (S=0, <math>2^1S_0</math> term). <math>\psi_A</math> is the wavefunction with antisymmetric spatial part and symmetric spin state <math>\chi_S</math>, i.e. the spin triplet (S=1, <math>2^3S_0</math> term).
| |
| − | Now consider the Coulomb energy <math>\frac{e^2}{r_{12}}</math> of the <math>e^--e^-</math> interaction in these excited states:
| |
| − | :<math>
| |
| − | \begin{split}
| |
| − | \Delta E &= \frac{1}{2}\int\int\frac{e^2}{r_{12}}[|\psi_{100}(r_1)|^2|\psi_{200}(r_2)|^2+(r_1\leftrightarrow r_2)] \\
| |
| − | &\pm\frac{1}{2}\int\int\frac{e^2}{r_{12}}[\psi_{100}^*(r_1)\psi_{200}^*(r_2)\psi_{100}(r_2)\psi_{200}(r_1)+(r_1\leftrightarrow r_2)]\\
| |
| − | &=\Delta
| |
| − | E^{Coul}\pm\Delta E^{exch}
| |
| − | \end{split}
| |
| − | </math>
| |
| − | The first term (called the Coulomb term, although both terms are Coulombic in origin) is precisely what we would calculate classically for the repulsion between two electron clouds of densities <math>|\psi_{100}|^2</math> and <math>|\psi_{200}^2|</math>. The second term, the exchange term, is a purely quantum mechanical effect associated with the Pauli exclusion principle. | |
| − | The triplet state has lower energy, because the antisymmetric spatial wavefuntion reduces <math>e^--e^-</math> repulsion interactions. Since the interaction energy is spin-dependent, it can be written in the same form as a ferromagnetic spin-spin interaction,
| |
| − | :<math>
| |
| − | \Delta E=\alpha+\beta\vec S_1\cdot\vec S_2.
| |
| − | </math>
| |
| − | To see this, we use the relation <math>\vec S_1\cdot\vec S_2=\frac{\vec S^2-\vec S_1^2-\vec S_2^2}{2}</math>. Since <math>\vec S_1^2 = \vec S_2^2 = \frac{3}{4}</math>, eq. \ref{eq:ferro} is equivalent to
| |
| − | :<math>
| |
| − | \begin{split}
| |
| − | \Delta E&=\alpha-\frac{3}{4}\beta+\frac{\beta}{2}\vec S^2\\
| |
| − | &=\underbrace{(\alpha-\frac{1}{4}\beta)}_{\Delta
| |
| − | E^{coul}}\pm\underbrace{(\frac{-\beta}{2})}_{\Delta E^{exch}},
| |
| − | \end{split}
| |
| − | </math>
| |
| − | where we have substituted <math>\vec S^2 = 0, 2</math> for the singlet and triplet states, respectively. Bear in mind that, although the interaction energy is spin-dependent, the origin of the coupling is electrostatic and not magnetic. Because of its electrostatic origin, the exchange energy (0.8 eV for the <math>^3S_1-^1S_0</math> splitting, as indicated in figure \ref{fig:he_levels}) is much larger than a magnetic effect such as the fine structure splitting, which carries an extra factor of <math>\alpha^2</math>.
| |
| − | \begin{figure}
| |
| − | <blockquote>
| |
| − | ::[[Image:atoms-he_intercombination|thumb|200px|none|]] | |
| − | (caption: Dipole-allowed transitions (solid) and intercombination lines (dashed) in helium.)
| |
| − | </blockquote>
| |
| − | \end{figure}
| |
| − | \QA{What field (coupling) drives singlet-triplet
| |
| − | transitions?
| |
| − | A. Optical fields (dipole operator)
| |
| − | B. rotating magnetic fields
| |
| − | C. Both
| |
| − | D. None
| |
| − | }{ | |
| − | Singlet-triplet transitions are forbidden by the <math>\Delta S=0</math> selection rule, so to first order the answer is D. A is ruled out because the dipole operator acts on the spatial wavefunction, not on the spin part. One might think (B) that a transverse magnetic field, which couples to <math>S_x,S_y</math>, <math>S_{x,y}=\frac{(S^+\pm iS)}{\sqrt{2}}</math>, can be used to flip a spin. However, a transverse <math>B</math> field can only rotate the two spins together; it cannot rotate one spin relative to the other, as would be necessary to change the magnitude of <math>\vec S=\vec{S}(1)+\vec{S}(2)</math>. Because all spin operators are symmetric against particle exchange, they couple only <math>S\leftrightarrow S, A\leftrightarrow A</math>. Thus, spatial and spin symmetry (S,A) are both good quantum numbers.
| |
| − | More formally, if all observables <math>\hat O</math> commute with the particle exchange operator <math>[P_{ij},\hat O]=0</math>, then <math>P_{12}</math> (S or A) is a good quantum number. Thus, as long as wavefunction and operators separate into spin dependent and space dependent parts <math>P_{12}=P_{12}^{SPACE}\cdot P_{12}^{SPIN}</math>, both <math>P_{12}</math>'s are conserved. Intercombination (i.e. transition between singlet and triplet) is only possible when this assumption is violated, i.e. when the spin and spatial wavefunctions are mixed, e.g. by spin orbit coupling.
| |
| − | As we will see in Ch. \ref{ch:fs}, spin orbit coupling is <math>\propto Z^4</math>, and hence is weak for helium. Thus, the <math>2^3S_1</math> state of helium is \textit{very} long-lived, with a lifetime of about 8,000 s. (footnote: Historically, the absence of transition between singlet and triplet states led to the belief that there were two kinds of helium, ortho-helium (triplet) and para-helium (singlet).) The other noble gases (Ne, Ar, Kr, Xe) have lifetimes on the order of 40 s.
| |
| − | Because they are so narrow, intercombination lines are of great interest for application in optical clocks. While a lifetime of 8000 s is \textit{too} long to be useful (because such a narrow transition is difficult both to find and to drive), intercombination lines in Mg, Ca, or Sr---with linewidths ranging from mHz to kHz---are discussed as potential optical frequency standards \cite{Ludlow2006, Ludlow2008}.
| |
| − | }
| |
| − | \begin{subappendices}
| |
| − | == Appendix: Solution of the Schr\"{o}dinger Equation == | |
| − | === Radial Schr\"{o}dinger equation for central potentials ===
| |
| − |
| |
| − | Stationary solutions of the time dependent
| |
| − | Schr\"{o}dinger equation
| |
| − | :<math>
| |
| − | i\hbar \frac{\partial \psi (\bf{r}, t)}{\partial t} = H (\bf{r})
| |
| − | \psi ({ \bf {r}}, t)
| |
| − | </math>
| |
| − | \noindent(<math>H</math> is the Hamiltonian operator ) can be represented as
| |
| − | :<math>
| |
| − | \psi {({\bf{r}}, t)} = e^{-iE_nt/\hbar}\psi_n (\bf{r}),
| |
| − | </math>
| |
| − | \noindent where <math>n</math> stands for all quantum numbers necessary to label the state. This
| |
| − | leads to the time-independent Schr\"{o}dinger equation
| |
| − | :<math>
| |
| − | [H ({\bf{r}}) - E_n] \psi_n (\bf{r}) = 0
| |
| − | </math>
| |
| − | A pervasive application of this equation in
| |
| − | atomic physics is fo the case of a spherically symmetric
| |
| − | one-particle system of mass <math>\mu</math>. In this case the
| |
| − | Hamiltonian is
| |
| − | <math><math> H \equiv~ \mbox{Kinetic~ Energy}~ +~ \mbox{Potential~ Energy}</math></math>
| |
| − | <math><math>= p^2 /2\mu + V(r)
| |
| − | = \frac{-\hbar^2 \nabla^2}{2 \mu} + V(r)</math></math>
| |
| − | :<math>
| |
| − | = - \frac{\hbar^2}{2\mu} {\left[ \frac{1}{r^2}
| |
| − | \frac{\partial}{\partial r} {\left( r^2\frac{\partial}{\partial
| |
| − | r}\right)} +\frac{1}{r^2 \sin \theta} \frac{\partial}{\partial
| |
| − | \theta} {\left( \sin \theta \frac{\partial}{\partial \theta}
| |
| − | \right)} + \frac{1}{r^2 \sin^2\theta}\frac{\partial^2}{\partial
| |
| − | \phi^2} \right]} + V(r)
| |
| − | </math>
| |
| − | \noindent where the kinetic energy operator <math>\nabla^2</math> has been written in
| |
| − | spherical coordinates. Because <math>V</math> is spherically symmetric, the angular
| |
| − | dependence of the solution is characteristic of spherically
| |
| − | symmetric systems in general and may be factored out:
| |
| − | :<math>
| |
| − | \psi_{n\ell m} ({\bf{r}}) = R_{n \ell}(r) Y_{\ell m} (\theta, \phi
| |
| − | )
| |
| − | </math>
| |
| − | \noindent <math>Y_{\ell m}</math> are the {\it spherical harmonics} and <math>\ell</math> is the
| |
| − | eigenvalue of the operator for the orbital angular momentum,
| |
| − | <math>L</math>,
| |
| − | :<math>
| |
| − | L^2 Y_{\ell m} = \ell (\ell+ 1) \hbar^2 Y_{\ell m}
| |
| − | </math>
| |
| − | and <math>m</math> is the eigenvalue of the projection of <math>L</math> on the
| |
| − | quantization axis (which may be chosen at will)
| |
| − | :<math>
| |
| − | L_z Y_{\ell m} = m \hbar Y_{\ell m}
| |
| − | </math>
| |
| − | With this substitution Eq.\ \ref{EQ_secpfive} the time
| |
| − | independent radial Schr\"{o}dinger equation becomes
| |
| − | :<math>
| |
| − | \frac{1}{r^2}\frac{d}{dr} {\left( r^2
| |
| − | \frac{dR_{n\ell}}{dr}\right)} + {\left[ \frac{2\mu}{\hbar^2}{\left[
| |
| − | E_{n\ell} - V(r)\right]} - \frac{\ell (\ell +1) }{r^2}\right]}
| |
| − | R_{n \ell} =0
| |
| − | </math>
| |
| − | This is the equation which is customarily solved for the hydrogen
| |
| − | atom's radial wave functions. For most applications (atoms,
| |
| − | scattering by a central potential, diatomic molecules) it is more
| |
| − | convenient to make a further substitution.
| |
| − | :<math>
| |
| − | R_{n\ell} (r) = y_{n\ell} (r)/r
| |
| − | </math>
| |
| − | which leads to
| |
| − | :<math>
| |
| − | \frac{d^2y_{n\ell} (r)}{dr^2} + {\left[ \frac{2\mu}{\hbar^2}
| |
| − | [E_{n\ell}-V(r)] - \frac{\ell (\ell +1)}{r^2}\right]}
| |
| − | y_{n\ell}(r)=0
| |
| − | </math>
| |
| − | with the boundary condition <math>y_{n\ell}(0) = 0</math>. This equation is
| |
| − | identical with the time independent Schr\"{o}dinger equation for a
| |
| − | particle of mass <math>\mu</math> in an effective one dimensional potential,
| |
| − | :<math>
| |
| − | V^{\rm eff}(r) = V(r) + L^2 /(2\mu r^2 ) = V(r) + \frac{\hbar^2
| |
| − | \ell (\ell +1)}{2\mu r^2}
| |
| − | </math>
| |
| − | The term <math>\hbar^2\ell ( \ell + 1 )/2 \mu r^2</math> is called the {\it
| |
| − | centrifugal potential}, and adds to the actual potential the
| |
| − | kinetic energy of the circular motion that must be present to
| |
| − | conserve angular
| |
| − | momentum.
| |
| − | === Radial equation for hydrogen ===
| |
| − | The quantum treatment of hydrogenic atoms or ions appears in
| |
| − | many textbooks and we present only a summary\footnote{The most comprehensive
| |
| − | treatment of hydrogen is the classic text of Bethe and Salpeter, { \it The
| |
| − | Quantum Mechanics of One- and Two-Electron
| |
| − | Atoms}, H. A. Bethe and E. E. Salpeter, Academic Press (1957). Messiah is also excellent.}.
| |
| − | For hydrogen Eq.\ \ref{EQ_secpten}
| |
| − | becomes
| |
| − | :<math>
| |
| − | \frac{d^2y_{n\ell}(r)}{dr^2} + {\left[\frac{2\mu}{\hbar^2} \left[
| |
| − | E_n + \frac{e^2}{r} \right] - \frac{\ell (\ell+1)}{r^2}\right]}
| |
| − | y_{n\ell}(r)=0
| |
| − | </math>
| |
| − | \noindent First look at this as <math>r \rightarrow 0</math>, the dominant terms are
| |
| − | :<math>
| |
| − | \frac{d^2y}{dr^2} - \frac{\ell (\ell +1)}{r^2} y=0
| |
| − | </math>
| |
| − | for any value of <math>E</math>. It is easily verified that the two
| |
| − | independent solutions are
| |
| − | :<math>
| |
| − | y \sim r^{\ell+1}~\mbox{and}~y \sim r^{-\ell}
| |
| − | </math>
| |
| − | For <math> \ell \geq 1</math> the only normalizable solution is <math>y \sim
| |
| − | r^{\ell + 1}</math>.
| |
| − | Question: What happens to these arguments for <math> \ell = 0</math>? What
| |
| − | implications does this have for the final solution? Messiah has a
| |
| − | good discussion of this.
| |
| − | We look next at the solution for <math>r \rightarrow \infty </math> where we
| |
| − | may investigate a simpler equation if <math> \lim_{r \rightarrow
| |
| − | \infty} rV(r) =0 </math>. For large r:
| |
| − | :<math>
| |
| − | \frac{d^2y}{dr^2} + \frac{2\mu E}{\hbar^2} y=0
| |
| − | </math>
| |
| − | If <math>E > 0</math>, this equation has oscillating solutions corresponding
| |
| − | to a free particle. For <math>E < 0</math> the equation has exponential
| |
| − | solutions, but only the decaying exponential is physically
| |
| − | acceptable (i.e.. normalizable)
| |
| − | :<math>
| |
| − | R(r)= y(r)/r= \frac{1}{r} e^{(- 2\mu E/\hbar^2)^\frac{1}{2} r}
| |
| − | </math>
| |
| − | When <math>E < 0</math>, it is possible to obtain physically reasonable
| |
| − | solutions to Eq.\ \ref{EQ_secpten}
| |
| − | (or indeed {\it any} bound state problem) only for certain
| |
| − | discrete values of <math>E</math>, its eigenvalues. This situation arises
| |
| − | from the requirement that the radial solution be normalizable, which requires
| |
| − | that
| |
| − | <math>\int_o^\infty y^2 (r) dr = 1</math>, or alternatively, that <math>y(r)</math> vanishes
| |
| − | sufficiently rapidly at large r.).
| |
| − | Eq.\
| |
| − | \ref{EQ_rehone} is a prescription
| |
| − | for generating a function <math>y(r)</math> for arbitrary <math>E < 0</math> given <math>y</math>
| |
| − | and <math>\mbox{d}y/\mbox{d} r</math> at
| |
| − | any point. This can be solved exactly as hydrogen. For other central
| |
| − | potentials, one can find the eigenvalues and eigenstates by
| |
| − | computation. One proceeds as follows:
| |
| − | Select a trial eigenvalue, <math>E < 0</math>. Starting at large <math>r</math> a
| |
| − | "solution" of the form of Eq.\ \ref{EQ_rehfive} is selected and
| |
| − | extended in to some intermediate value of <math>r, ~r_m</math>. At the
| |
| − | origin one must select the solution of the form <math>y_{\ell} \sim
| |
| − | r^{\ell + 1}</math> Eq.\ (\ref{EQ_rehthree}); this "solution" is then
| |
| − | extended out to <math>r_m</math>. The two "solutions" may be made to have
| |
| − | the same value at <math>r_m</math> by multiplying one by a constant;
| |
| − | however, the resulting function is a valid solution only if the
| |
| − | first derivative is continuous at <math>r_m</math>, and this occurs only for
| |
| − | a discrete set of <math>E_{n \ell}</math>. The procedure described here is,
| |
| − | in fact, the standard Numerov-Cooley algorithm for finding bound
| |
| − | states. Its most elegant feature is a
| |
| − | procedure for adjusting the
| |
| − | trial eigenvalue using the discontinuity in the derivative that converges to the
| |
| − | correct energy very rapidly.
| |
| − | For the hydrogen atom, the eigenvalues can be determined
| |
| − | analytically. The substitution
| |
| − | :<math>
| |
| − | y_{\ell}(r) = r^{\ell +1} e^{-(-2\mu E/\hbar^2)^{1/2}r} v_{\ell}
| |
| − | (r)
| |
| − | </math>
| |
| − | leads to a particularly simple equation. To make it
| |
| − | dimensionless, one changes the variable from <math>r</math> to <math>x</math>
| |
| − | :<math>
| |
| − | x=[2(-2\mu E)^{1/2}/\hbar ]r
| |
| − | </math>
| |
| − | so the exponential in Eq.\ \ref{EQ_rehsix} becomes <math>e^{- 1/2 x}
| |
| − | )</math>, and defines
| |
| − | :<math>
| |
| − | v=\frac{\hbar}{(-2\mu E)^{1/2}a_o}
| |
| − | </math>
| |
| − | where <math>a_o</math> is the Bohr radius:
| |
| − | :<math>
| |
| − | {\left[ x \frac{d^2}{dx^2} + (2\ell +2 -x) \frac{d}{dx} - (\ell +
| |
| − | 1-v)\right]} v_{\ell} = 0
| |
| − | </math>
| |
| − | This is a Laplace equation and its solution is a confluent
| |
| − | hypergeometric series. To find the
| |
| − | eigenvalues one now tries a Taylor series
| |
| − | :<math>
| |
| − | v_{\ell}(x) = 1+a_1 x + a_2 x^2 + \cdots
| |
| − | </math>
| |
| − | for <math>v_{\ell}</math>. This satisfies the equation only if the
| |
| − | coefficients of each power of x are satisfied, i.e..\
| |
| − | :<math>\begin{array}{rcl}
| |
| − | x^o:&&(2\ell +2) a_1 - (\ell + 1 - v) =0 \\
| |
| − | x^1:&& 2(2\ell + 3) a_2 - (\ell +2 -v)a_{\ell} =0\\
| |
| − | x^{p-1}:&& p(2\ell + 1 + p)a_p -(\ell + p -v) a_{p-1} = 0
| |
| − |
| |
| − | \end{array}</math>
| |
| − | The first line fixes <math>a_1</math>, the second then determines <math>a_2</math>, and
| |
| − | in general
| |
| − | :<math>
| |
| − | a_p = \frac{(\ell + p-v)}{p(2\ell + 1 + p)}a_{p-1}
| |
| − | </math>
| |
| − | In general Eq.\ \ref{EQ_reheleven} will give a <math>p^{th}</math>
| |
| − | coefficient on the order of 1/<math>p</math>! so
| |
| − | :<math>
| |
| − | v_{\ell}(x)\sim \sum_{p=0} x^p/p!=e^x
| |
| − | </math>
| |
| − | this spells disaster because it means <math>y = r^{\ell + 1} e^{- x/2}
| |
| − | v_{\ell} (r)</math> diverges. The only way in which this can be
| |
| − | avoided is if the series truncates, i.e. if v is an integer:
| |
| − | :<math>
| |
| − | v=n=n^\prime +\ell +1 ~~~~~~~~~~n=0,1,2,\cdots
| |
| − | </math>
| |
| − | so that <math>a_n</math>, will be zero and <math>v_{\ell}</math> will have <math>n^\prime </math>
| |
| − | nodes. Since <math>n^\prime \geq = 0</math>, it is clear that you must look
| |
| − | at energy level <math>n \geq \ell + 1</math> to find a state with angular
| |
| − | momentum <math>\ell</math> (e.g.. the 2<math>d</math> configuration does not exist).
| |
| − | This gives the eigenvalues of hydrogen (from Eq.\
| |
| − | \ref{EQ_reheight})
| |
| − | :<math>
| |
| − | E_n=-\frac{1}{2} \alpha^2 \mu c^2/(n^\prime + \ell + 1)^2 =
| |
| − | -\frac{1}{2} \frac{\mu (e^2/4 \pi \epsilon_o)^2}{\hbar^2}\frac{1}{n^2} = - \frac{hcR_H }{n^2},
| |
| − | </math>
| |
| − | which agrees with the Bohr formula.
| |
| | == Appendix: More on the Quantum Defect == | | == Appendix: More on the Quantum Defect == |
| − | === Explanation: JWKB Approach ===
| + | |
| − | It must always be kept in mind that the quantum defect is a
| + | See [[More on the Quantum Defect]] |
| − | phenomenological result. To explain how such a simple result
| + | |
| − | arises is obviously an interesting challenge, but it is not to be
| + | == Appendix: Metrology and Precision Measurement and Units == |
| − | expected that the solution of this problem will lead to great new
| + | |
| − | physical insight. The only new results obtained from
| + | See [[Metrology and Precision Measurement and Units]] |
| − | understanding quantum defects in one electron systems are the
| + | |
| − | connection between the quantum defect and the electron scattering
| + | == References == |
| − | length for the same system (Mott and Massey section III 6.2)
| + | |
| − | which may be used to predict low energy electron scattering cross
| + | <ul><li> '''CohenT''': Claude Cohen-Tannoudji, Bernard Diu, and Franck Laloë. ''Quantum Mechanics''. Hermann, Paris, 1977. |
| − | sections (ibid. XVII 9&10), and the simple expressions relating
| + | <li> '''Freeman1976''': Richard R. Freeman and Daniel Kleppner. Core polarization and quantum defects in high-angular-momentum states of alkali atoms. ''Phys. Rev. A'', 14(5):1614–1619, Nov 1976. |
| − | <math>\delta_L</math> to the polarizability of the core for larger
| + | <li> '''Gasiorowicz''': Stephen Gasiorowicz. ''Quantum Physics''. Wiley, 2003. |
| − | <math>\delta_L</math> \cite{Freeman1976}. The principal use of the quantum defect
| + | <li> '''Landau''': L. D. Landau and L. M. Lifshitz. ''Quantum Mechanics: Non-Relativistic Theory''. Elsevier Science, 1977. |
| − | is to predict the positions of higher terms in a series for
| + | <li> '''Ludlow2006''': A. D. Ludlow, M. M. Boyd, T. Zelevinsky, S. M. Foreman, S. Blatt, M. Notcutt, T Ido, and J. Ye. Systematic study of the sr-87 clock transition in an optical lattice. ''Physical Review Letters'', 96(3):033003, 2006. |
| − | which <math>\delta_L</math> is known.
| + | <li> '''Ludlow2008''': A. D. Ludlow, T. Zelevinsky, G. K. Campbell, S. Blatt, M. M. Boyd, M. H. G. de Miranda, M. J. Martin, J. W. Thomsen, S. M. Foreman, Jun Ye, T. M. Fortier, J. E. Stalnaker, S. A. Diddams, Y. Le Coq, Z. W. Barber, N. Poli, N. D. Lemke, K. M. Beck, and C. W. Oates. Sr lattice clock at <math>1\times 10^{-16}</math> fractional uncertainty by remote optical evaluation with a ca clock. ''Science'', page 1153341, 2008. |
| − | Explanations of the quantum defect range from the elaborate fully
| + | <li> '''codata2002''': Peter J. Mohr, Barry N. Taylor, and David B. Newell. CODATA recommended values of the fundamental physical constants: 2002. ''Rev. Mod. Phys.'', 77, Jan 2005. Available online at <url> |
| − | quantal explanation of Seaton \cite{Seaton1966} to the extremely simple
| + | |
| − | treatment of Parsons and Weisskopf \cite{Parsons1967}, who assume that
| + | </url>http://physics.nist.gov/constants. |
| − | the electron can not penetrate inside the core at all, but use the
| + | <li> '''Parsons1967''': R. G. Parsons and V. F. Weisskopf. ''Z. Phys.'', 202:492, 1967. |
| − | boundary condition <math>R (r_c ) = 0</math> which requires relabeling the
| + | <li> '''Seaton1966''': M. J. Seaton. ''Proc. Phys. Soc.'', 88:801, 1966. |
| − | lowest <math>ns</math> state 1s since it has no nodes outside the core. This
| + | <li> '''Hodgman2009''': S.S. Hodgman, R.G. Dall, L.J. Byron, K.G.H. Baldwin, S.J. Buckman, and A.G. Truscott. ''Phys. Rev. Lett.'', 103:053002, 2009. |
| − | viewpoint has a lot of merit because the exclusion principle and
| + | </ul> |
| − | the large kinetic energy of the electron inside the core combine
| + | <br style="clear: both" /> |
| − | to reduce the amount of time it spends in the core. This is
| + | |
| − | reflected in the true wave function which has <math>n</math> nodes in the
| + | |
| − | core and therefore never
| + | [[Category:8.421]] |
| − | has a chance to reach a large amplitude in this region.
| |
| − | To show the physics without much math (or rigor) we turn to the
| |
| − | JWKB solution to the radial Schr\"{o}dinger Equation (see Messiah Ch.\
| |
| − | VI). Defining the wave number
| |
| − | :<math>
| |
| − | k_{\ell} (r) = \sqrt{2m[E-V_{\rm eff}(r) ]\hbar}
| |
| − | ~~(\mbox{remember}~ V_{\rm eff}~~\mbox{depends~on}~ \ell )
| |
| − | </math>
| |
| − | then the phase accumulated in the classically allowed region is
| |
| − | :<math>
| |
| − | \phi_{\ell} (E) = \int_{r_i}^{r_o} k_{\ell} (r) dr
| |
| − | </math>
| |
| − | where <math>r_i</math> and <math>r_o</math> are the inner and outer turning points.
| |
| − | Bound state eigenvalues are found by setting
| |
| − | :<math>
| |
| − | [\phi_{\ell} (E) -\pi /2] = n\pi
| |
| − | </math>
| |
| − | (The <math>\pi / 2</math> comes from the connection formulae and would be 1/4
| |
| − | for <math>\ell</math> = 0 state where <math>r_i = 0</math>. Fortunately it cancels
| |
| − | out.)
| |
| − | To evaluate <math>\phi (E)</math> for hydrogen use the Bohr formula for
| |
| − | <math>n(E)</math>,
| |
| − | :<math> | |
| − | \phi_H(E) = \pi (hcR_H /E)^{1/2} + \pi
| |
| − | /2~~~\mbox{(independent~of~}\ell)
| |
| − | </math>
| |
| − | In the spirit of the JWKB approximation, we regard the phase as a
| |
| − | continuous function of <math>E</math>. Now consider a one-electron atom with
| |
| − | a core of inner shell electrons that lies entirely within <math>r_c</math>. Since it has a
| |
| − | hydrogenic potential outside of <math>r_c</math>, its phase can be written
| |
| − | (where <math>r_{oH} , r_{iH}</math> are the outer and inner turning points
| |
| − | for hydrogen at energy <math>E</math>):
| |
| − | <math><math>\phi_{\ell}(E) = \int_{r_i}^{r_{oH}} k_{\ell}(r) dr =
| |
| − | \int_{r_i}^{r_c} k_{\ell} (r) dr + \int_{r_c}^{r_{oH}} k_H(r) dr</math></math>
| |
| − | <math><math> = \int_{r_i}^{r_c} k(r) dr -
| |
| − | \int_{r_{iH}}^{r_{c}} k_H (r) dr + \int_{r_{iH}}^{r_{oH}} k_H(r)
| |
| − | dr</math></math>
| |
| − | The final integral is the phase for hydrogen at some energy <math>E</math>,
| |
| − | and can be written as <math>\phi_H(E) = (n* + 1/2)\pi</math>. Designating
| |
| − | the sum of the first two integrals by the phase <math>\delta \phi</math>,
| |
| − | then we have
| |
| − | :<math>
| |
| − | \delta\phi + (n* + 1/2)\pi = (n + 1/2)\pi
| |
| − | </math>
| |
| − | \noindent or
| |
| − | :<math>
| |
| − | n* = n - \delta\phi/\pi
| |
| − | </math>
| |
| − | Hence, we can relate the quantum defect to a phase:
| |
| − | :<math>
| |
| − | \delta_{\ell}= \left[ \int_{r_i}^{r_c} k(r) dr -
| |
| − | \int_{r_{iH}}^{r_{c}} k_H (r) dr \right] \frac{1}{\pi}
| |
| − | </math>
| |
| − | \noindent since it is clear from Eq.\ \ref{EQ_expone} and the fact that the
| |
| − | turning point is determined by <math>E + V_{\rm eff} (r_i ) = 0</math> that
| |
| − | <math>\delta_\ell</math> approaches a constant as <math>E\rightarrow 0</math>.
| |
| − | Now we can find the bound state energies for the atom with a
| |
| − | core; starting with Eq.\ \ref{EQ_expthree},
| |
| − | <math><math>n\pi = \phi (E) -\pi /2</math></math> | |
| − | <math><math> = \pi \delta_L (E) + \pi (hcR_H /E )^{1/2}</math></math>
| |
| − | :<math> | |
| − | \Rightarrow E = hcR_H /[n-\delta_L (E)]^2 \equiv
| |
| − | \frac{hcR_H}{[n-\delta_{\ell}^{(0)} + \delta_{\ell}^{(1)} hcR_H
| |
| − | /n^2]^2}
| |
| − | </math>
| |
| − | thus we have explained the Balmer-Ritz formula
| |
| − | (Eq.\ \ref{EQ_phenthree}).
| |
| − | If we look at the radial Schr\"{o}dinger equation for the electron
| |
| − | ion core system in the region where <math>E > 0</math> we are dealing with
| |
| − | the scattering of an electron by a modified Coulomb potential
| |
| − | (Mott & Massey Chapter 3). Intuitively one would expect that
| |
| − | there would be an intimate connection between the bound state
| |
| − | eigenvalue problem described earlier in this chapter and this
| |
| − | scattering problem, especially in the limit <math>E \rightarrow 0</math>
| |
| − | (from above and below). Since the quantum defects characterize
| |
| − | the bound state problem accurately in this limit one would expect
| |
| − | that they should be directly related to the scattering phase
| |
| − | shifts <math>\sigma_{\ell} (k)</math> (<math>k</math> is the momentum of the {\it free}
| |
| − | particle) which obey
| |
| − | :<math>
| |
| − | \lim_{k\rightarrow 0} \cot[\sigma_{\ell} (k)]=\pi\delta_{\ell}^o
| |
| − | </math>
| |
| − | This has great intuitive appeal: <math>\pi \delta_{\ell}^o</math> as
| |
| − | discussed above is precisely the phase shift of the wave function
| |
| − | with the core present relative to the one with V = <math>e^2 / r</math>. On
| |
| − | second thought Eq.\ \ref{EQ_expeight} might appear puzzling since
| |
| − | the scattering phase shift is customarily defined as the shift
| |
| − | relative to the one with <math>V = 0</math>. The resolution of this paradox
| |
| − | lies in the long range nature of the Coulomb interaction; it
| |
| − | forces one to redefine the scattering phase shift, <math>\sigma_{\ell}
| |
| − | (k)</math>, to be the shift relative to a pure Coulomb potential. | |
| − | === Quantum defects for a model atom ===
| |
| − |
| |
| − | Now we give a calculation of a quantum defect for a potential
| |
| − | <math>V(r)</math> which is not physically realistic, but has only the virtue
| |
| − | that it is easily solvable. The idea is to put an extra term in
| |
| − | the potential which goes as <math>1/r^2</math> so that the radial
| |
| − | Schr\"{o}dinger equation (Eq.\ \ref{EQ_secpten}) can be solved
| |
| − | simply by adjusting <math>\ell</math>. The electrostatic potential
| |
| − | corresponds to having all the core electrons in a small cloud of
| |
| − | size <math>r_n</math> (which is a nuclear size) which decays as an inverse
| |
| − | power of <math>r</math>.
| |
| − | <math><math>\phi_{\ell} (r) = \frac{e}{r} + \frac{(Z-1) er_n}{2r^2}</math></math>
| |
| − | <math><math>\Rightarrow E(r) = \frac{e}{r^2} + \frac{(Z-1)er_n}{r^3}</math></math>
| |
| − | <math><math>\Rightarrow Q_{\rm inside} (r) = e + \frac{(Z-1)er_n}{r}</math></math>
| |
| − | :<math> | |
| − | \Rightarrow \rho (r) = \frac{dQ/dr}{4\pi r^2} = - (Z-1) er_n /4\pi
| |
| − | r^4
| |
| − | </math>
| |
| − | At <math>r =r_n</math>, <math>Q_{\rm inside}(r_n) = Z e</math>. We presume <math>r_n</math> is
| |
| − | the nuclear size and pretend that it is so small we don't have to
| |
| − | worry about what happens inside it.
| |
| − | When the potential V (r) = <math>- e \phi (r)</math> is substituted in Eq.\
| |
| − | \ref{EQ_rehone}, one has
| |
| − | :<math>
| |
| − | \frac{d^2y}{dr^2} +{\left[ \frac{2\mu}{\hbar^2} {\left[ E_n +
| |
| − | \frac{e^2}{r}\right]} - \frac{\ell (\ell + 1)-A}{r^2} \right]} y=0
| |
| − | </math>
| |
| − | :<math>
| |
| − | \mbox{where} ~~~ A = \frac{2\mu (Z-1) e^2 r_n}{\hbar^2}
| |
| − | </math>
| |
| − | If one now defines
| |
| − | :<math> | |
| − | \ell^\prime ( \ell^\prime +1) = \ell( \ell +1) - A
| |
| − | </math>
| |
| − | then <math>\ell^\prime < \ell</math> since <math>A >0</math>, and one can write
| |
| − | :<math>
| |
| − | \ell^\prime = \ell - \delta_{\ell}
| |
| − | </math>
| |
| − | Substituting Eq.\ \ref{EQ_qdancfour} in Eq.\ \ref{EQ_qdanctwo}
| |
| − | gives the radial Schr\"{o}dinger equation for hydrogen, (Eq.\ref{EQ_secpten}),
| |
| − | except that <math>\ell^\prime</math> replaces <math>\ell</math>;
| |
| − | eigenvalues occur when (see Eq.\ \ref{EQ_rehfourteen})
| |
| − | :<math>
| |
| − | v= n^\prime + \ell^\prime + 1 = n^* ~~~~~n^\prime = 0, 1, 2,
| |
| − | \cdots
| |
| − | </math>
| |
| − | where <math>n^\prime</math> is an integer. Using <math>n = n^\prime + \ell + 1</math> as
| |
| − | before, we obtain the corresponding eigenvalues as
| |
| − | :<math>
| |
| − | E_n = hcR_H /n^{*2} = hcR_H /(n-\delta_{\ell} )^2
| |
| − | </math>
| |
| − | The quantum defect is independent of <math>E</math>
| |
| − | :<math>
| |
| − | \delta_{\ell} = \ell - \ell^\prime = n-n^*
| |
| − | </math>
| |
| − | Eq.\ \ref{EQ_qdancfour} may be solved for <math>\delta_{\ell}</math> using
| |
| − | the standard quadratic form. Retaining the solution which
| |
| − | <math>\rightarrow 0</math> as <math>Z\rightarrow 1</math>, gives
| |
| − | :<math>
| |
| − | \delta_{\ell} = (\ell + 1/2 ) - \sqrt{(\ell + 1/2 )^2 -A} \approx
| |
| − | \frac{A}{2\ell + 1}~\mbox{for}~~ A << \ell + 1/2
| |
| − | </math>
| |
| − | This shows that <math>\delta_{\ell} \rightarrow 0</math> as <math>\ell \rightarrow
| |
| − | \infty</math>.
| |
| − | In contrast to the predictions of the above simple model, quantum
| |
| − | defects for realistic core potentials decrease much more rapidly
| |
| − | with increasing <math>\ell</math> [for example as (<math>\ell + 1/2)^{-3} ]</math> and
| |
| − | generally exhibit <math>\delta_{\ell}^{(0)}</math> close to zero for all
| |
| − | <math>\ell</math> greater than
| |
| − | the largest <math>\ell</math> value occupied by electrons in the core.
| |
| − | == Metrology and Precision Measurement and Units ==
| |
| − | As scientists we take the normal human desire to understand the
| |
| − | world to quantitative extremes. We demand agreement of theory and
| |
| − | experiment to the greatest accuracy possible. We measure
| |
| − | quantities way beyond the current level of theoretical
| |
| − | understanding in the hope that this measurement will be valuable
| |
| − | as a reference point or that the difference between our value and
| |
| − | some other nearly equal or simply related quantity will be
| |
| − | important. The science of measurement, called metrology, is
| |
| − | indispensable to this endeavor because the accuracy of
| |
| − | measurement limits the accuracy of experiments and their
| |
| − | intercomparison. In fact, the construction, intercomparison, and
| |
| − | maintenance of a system of units is really an art (with some, a
| |
| − | passion), often dependent on the latest advances in the art of
| |
| − | physics (e.g.. quantized Hall effect, cold atoms, trapped particle
| |
| − | frequency standards).
| |
| − | As a result of this passion, metrological precision typically
| |
| − | marches forward a good fraction of an order of magnitude per
| |
| − | decade. Importantly, measurements of the same quantity (e.g.
| |
| − | <math>\alpha</math> or <math>e/h</math>) in different fields of physics (e.g.. atomic | |
| − | structure, QED, and solid state) provide one of the few
| |
| − | cross-disciplinary checks available in a world of increasing
| |
| − | specialization. Precise null experiments frequently rule out
| |
| − | alternative theories, or set limits on present ones. Examples
| |
| − | include tests of local Lorentz invariance, and the equivalence
| |
| − | principle, searches for atomic lines forbidden by the exclusion
| |
| − | principle, searches for electric dipole moments (which violate
| |
| − | time reversal invariance), and the recent searches for a
| |
| − | "fifth [gravitational] force".
| |
| − | A big payoff, often involving new physics, sometimes comes from
| |
| − | attempts to achieve routine progress. In the past, activities
| |
| − | like further splitting of the line, increased precision and
| |
| − | trying to understand residual noise have lead to the fine and
| |
| − | hyperfine structure of <math>H</math>, anomalous Zeeman effect, Lamb shift,
| |
| − | and the discovery of the 3K background radiation. One hopes that
| |
| − | the future will bring similar surprises. Thus, we see that
| |
| − | precision experiments, especially involving fundamental constants
| |
| − | or metrology not only solidify the foundations of physical
| |
| − | measurement and theories, but occasionally open new frontiers.
| |
| − | === Dimensions and Dimensional Analysis ===
| |
| − | Oldtimers were brought up on the mks system - meter, kilogram,
| |
| − | and second. This simple designation emphasized an important
| |
| − | fact: three dimensionally independent units are sufficient to
| |
| − | span the space of all physical quantities. The dimensions are
| |
| − | respectively <math>\ell</math> - length, <math>m</math>-mass, and <math>t</math>-time. These
| |
| − | three dimensions suffice because when a new physical quantity is
| |
| − | discovered (e.g.. charge, force) it always obeys an equation which
| |
| − | permits its definition in terms of m,k, and s. Some might argue
| |
| − | that fewer dimensions are necessary (e.g.. that time and distance
| |
| − | are the same physical quantity since they transform into each
| |
| − | other in moving reference frames); we'll keep them both, noting
| |
| − | that the definition of length is now based on the speed of
| |
| − | light. Practical systems of units have additional units beyond
| |
| − | those for the three dimensions, and often additional "as
| |
| − | defined" units for the same dimensional quantity in special
| |
| − | regimes (e.g.. x-ray wavelengths or atomic masses).
| |
| − | Dimensional analysis consists simply in determining for each
| |
| − | quantity its dimension along the three dimensions (seven if you
| |
| − | use the SI system rigorously) of the form
| |
| − | \[
| |
| − | \text{Dimension}(G) \equiv [G] = m^{-1}l^3 t^{-2}
| |
| − | \]
| |
| − | Dimensional analysis yields an estimate for a given unknown
| |
| − | quantity by combining the known quantities so that the dimension
| |
| − | of the combination equals the dimension of the desired unknown.
| |
| − | The art of dimensional analysis consists in knowing whether the
| |
| − | wavelength or height of the water wave (both with dimension <math>l</math>)
| |
| − | is the length to be combined with the density of water and the
| |
| − | local gravitational acceleration to predict the speed of the
| |
| − | wave.
| |
| − | === SI units ===
| |
| − | A single measurement of a physical quantity, by itself, never
| |
| − | provides information about the physical world, but only about the
| |
| − | size of the apparatus or the units used. In order for a single
| |
| − | measurement to be significant, some other experiment or
| |
| − | experiments must have been done to measure these "calibration"
| |
| − | quantities. Often these have been done at an accuracy far
| |
| − | exceeding our single measurement so we don't have to think twice
| |
| − | about them. For example, if we measure the frequency of a
| |
| − | rotational transition in a molecule to six digits, we have hardly
| |
| − | to worry about the calibration of the frequency generator if it is a
| |
| − | high accuracy model that is good to nine digits. And if we are concerned
| |
| − | we can
| |
| − | calibrate it with an accuracy of several more orders of magnitude
| |
| − | against station WWV or GPS satellites which give time valid to 20
| |
| − | ns
| |
| − | or so.
| |
| − | Time/frequency is currently the most accurately measurable
| |
| − | physical quantity and it is relatively easy to measure to
| |
| − | <math>10^{-12}</math>. In the SI (System International, the agreed-upon
| |
| − | systems of weights and measures) the second is defined as
| |
| − | 9,192,631,770 periods of the Cs hyperfine oscillation in zero
| |
| − | magnetic field. Superb Cs beam machines at places like
| |
| − | NIST-Boulder provide a realization of this definition at about
| |
| − | <math>10^{-14}</math>. Frequency standards based on laser-cooled atoms and
| |
| − | ions have the potential to do several orders of magnitude better
| |
| − | owing to the longer possible measurement times and the reduction
| |
| − | of Doppler frequency shifts. To give you an idea of the
| |
| − | challenges inherent in reaching this level of precision, if you
| |
| − | connect a 10 meter coaxial cable to a frequency source good at
| |
| − | the <math>10^{-16}</math> level, the frequency coming out the far end in a
| |
| − | typical lab will be an order of magnitude less stable - can you
| |
| − | figure out why?
| |
| − | The meter was defined at the first General Conference on Weights
| |
| − | and Measures in 1889 as the distance between two scratches on a
| |
| − | platinum-iridium bar when it was at a particular temperature (and
| |
| − | pressure). Later it was defined more democratically, reliably, and
| |
| − | reproducibly in terms of the wavelength of a certain orange
| |
| − | krypton line. Most recently it has been defined as the distance
| |
| − | light travels in 1/299,792,458 of a second. This effectively
| |
| − | defines the speed of light, but highlights the distinction between
| |
| − | defining and realizing a particular unit. Must you set up a
| |
| − | speed of light experiment any time you want to measure length?
| |
| − | No: just measure it in terms of the wavelength of a He-Ne laser
| |
| − | stabilized on a particular hfs component of a particular methane
| |
| − | line within its tuning range; the frequency of this line has been
| |
| − | measured to about a part in <math>10^{-11}</math> and it may seem that your
| |
| − | problem is solved. Unfortunately the reproducibility of the
| |
| − | locked frequency and problems with diffraction in your
| |
| − | measurement both limit length measurements at about <math>10^{-11}</math>.
| |
| − | A list of spectral lines whose frequency is known to better than
| |
| − | <math>10^{-9}</math> is given in Appendix II of the NIST special publication
| |
| − | #330, available of the www at\footnote{
| |
| − | http://physics.nist.gov/Pubs/SP330/cover.html} - see both | |
| − | publications and reference data. The latest revision of the
| |
| − | fundamental constants CODATA is available from NIST at
| |
| − | http://physics.nist.gov/constants , and a previous version is published
| |
| − | in Reference \cite{codata2002}.
| |
| − | The third basic unit of the SI system is kilogram, the only
| |
| − | fundamental SI base unit still defined in terms of an artifact -
| |
| − | in this case a platinum-iridium cylinder kept in clean air at the
| |
| − | Bureau de Poids et Measures in Severes, France. The dangers of
| |
| − | mass change due to cleaning, contamination, handling, or accident
| |
| − | are so perilous that this cylinder has been compared with the
| |
| − | dozen secondary standards that reside in the various national
| |
| − | measurement laboratories only two times in the last century.
| |
| − | Clearly one of the major challenges for metrology is
| |
| − | replacement of the artifact kilogram with an atomic definition.
| |
| − | This could be done analogously with the definition of length by
| |
| − | defining Avogadro's number. While atomic mass can be measured to
| |
| − | <math>10^{-11}</math>, there is currently no sufficiently accurate method of
| |
| − | realizing this definition, however. (The unit of atomic mass,
| |
| − | designated by <math>\mu</math> is 1\\12 the mass of a <math>^{12}</math>C
| |
| − | atom.)
| |
| − | There are four more base units in the SI system - the ampere,
| |
| − | kelvin, mole, and the candela - for a total of seven. While
| |
| − | three are sufficient (or more than sufficient) to do physics, the
| |
| − | other four reflect the current situation that electrical
| |
| − | quantities, atomic mass, temperature, and luminous intensity can
| |
| − | be and are regularly measured with respect to auxiliary standards
| |
| − | at levels of accuracy greater than that with which can be
| |
| − | expressed in terms of the above three base units. Thus
| |
| − | measurements of Avogadro's constant, the Boltzmann constant, or
| |
| − | the mechanical equivalents of electrical units play a role of
| |
| − | interrelating the base units of mole (number of atoms of <math>^{12}</math>C
| |
| − | in 0.012 kg of <math>^{12}</math>C), kelvin, or the new de facto volt and ohm
| |
| − | (defined in terms of Josephson and quantized Hall effects
| |
| − | respectively). In fact independent measurement systems exist for
| |
| − | other quantities such as x-ray wavelength (using diffraction from
| |
| − | calcite or other standard crystals), but these other de facto
| |
| − | measurement scales are not
| |
| − | formally sanctioned by the SI system.
| |
| − | === Metrology ===
| |
| − | The preceding discussion gives a rough idea of the definitions
| |
| − | and realizations of SI units, and some of the problems that arise
| |
| − | in trying to define a unit for some physics quantity (e.g.. mass)
| |
| − | that will work across many orders of magnitudes. However, it
| |
| − | sidesteps questions of the border between metrology and precision
| |
| − | measurements. (Here we have used the phrase "precision
| |
| − | measurement" colloquially to indicate an accurate absolute
| |
| − | measurement; if we were verbally precise, precision would imply
| |
| − | only excellent relative accuracy.)
| |
| − | It is clear that if we perform an experiment to measure
| |
| − | Boltzmann's constant we are not learning any fundamental physics;
| |
| − | we are just measuring the ratio of energy scales defined by our
| |
| − | arbitrary definitions of the first three base units on the one
| |
| − | hand and the thermal energy of the triple point of water on the
| |
| − | other. This is clearly a metrological experiment. Similarly,
| |
| − | measuring the hfs frequency of Cs would be a metrological
| |
| − | experiment in that it would only determine the length of the
| |
| − | second.
| |
| − | If we measure the hfs frequency of <math>H</math> with high accuracy, this
| |
| − | might seem like a physics experiment since this frequency can be
| |
| − | predicted theoretically. Unfortunately theory runs out of gas at
| |
| − | about <math>10^{-6}</math> due to lack of accurate knowledge about the
| |
| − | structure of the proton (which causes a 42 ppm shift). Any digits
| |
| − | past this are just data collection until one gets to the 14th, at
| |
| − | which point one becomes able to use a <math>H</math> maser as a secondary
| |
| − | time standard. This has stability advantages over Cs beams for
| |
| − | time periods ranging from seconds to days and so might be
| |
| − | metrologically useful -- in fact, it is widely used in very long
| |
| − | baseline radio astronomy.
| |
| − | One might ask "Why use arbitrarily defined base units when
| |
| − | Nature has given us quantized quantities already?" Angular
| |
| − | momentum and charge are quantized in simple multiples of <math>\hbar</math>
| |
| − | and <math>e</math>, and mass is quantized also although not so simply. We
| |
| − | then might define these as the three main base units - who says
| |
| − | we have to use mass, length and time? Unfortunately the
| |
| − | measurements of <math>e, \hbar</math>, and <math>N_A^{-1}</math> (which may be thought
| |
| − | of as the mass quantum in grams) are only accurate at about the
| |
| − | <math>10^{-8}</math> level, well below the accuracy of the realization of the
| |
| − | current
| |
| − | base units of SI.
| |
| − | The preceding discussion seems to imply that measurements of
| |
| − | fundamental constants like <math>e, \hbar</math>, and <math>N_A^{-1}</math> are merely
| |
| − | determinations of the size of SI units in terms of the quanta of
| |
| − | Nature. In reality, the actual state of affairs in the field of
| |
| − | fundamental constants is much more complicated. The complication
| |
| − | arises because there are not single accurate experiments that
| |
| − | determine these quantities - real experiments generally determine
| |
| − | some combination of these, perhaps with some other calibration
| |
| − | type
| |
| − | variables thrown in (e.g.. the lattice spacing of Si crystals).
| |
| − | To illustrate this, consider measurement of the Rydberg constant,
| |
| − | :<math> | |
| − | Ry_\infty = \frac{m_e e^4}{(4\pi )^3 \epsilon_0^2 \hbar_c^3}
| |
| − | </math>
| |
| − | a quantity which is an inverse length (an energy
| |
| − | divided by <math>\hbar c</math>), closely related to the number of
| |
| − | wavelengths per cm of light emitted by a <math>H</math> atom (the units are
| |
| − | often given in spectroscopists' units, <math>cm^{-1}</math>, to the dismay
| |
| − | of SI purists). Clearly such a measurement determines a linear
| |
| − | combination of the desired fundamental quantities. Too bad,
| |
| − | because it has recently been measured by several labs with
| |
| − | results that agree to <math>10^{-11}</math>. (In fact, the quantity
| |
| − | that is measured is the Rydberg frequency for hydrogen, <math>cRy_H</math>,
| |
| − | since there is no way to measure wavelength to such precision.)
| |
| − | This example
| |
| − | illustrates a fact of life of precision experiments: with care
| |
| − | you can trust the latest adjustment of the fundamental constants
| |
| − | and the metrological realizations of physical quantities at
| |
| − | accuracies to <math>10^{-7}</math>; beyond that the limit on your
| |
| − | measurement may well be partly metrological. In that case, what you measure
| |
| − | is not in general clearly related to one single fundamental
| |
| − | constant or metrological quantity. The results of your
| |
| − | experiment will then be incorporated into the least squares
| |
| − | adjustment of the fundamental constants, and the importance of
| |
| − | your experiment is determined by the size of its error bar
| |
| − | relative to the uncertainty of all other knowledge about the
| |
| − | particular linear combination of fundamental and metrological
| |
| − | variables that you have measured.
| |
| − | \end{subappendices}
| |
| − | \putbib
| |
Introduction
We could have continued our discussion of two-level systems and
resonance and introduced line shapes and various modes of
excitation---but first we want to look where the lines come from: from
atomic structure. We'll begin by considering the electronic structure
in hydrogen and, more generally, atoms with one valence electron, then
study the case of helium to understand the effect of adding a second
electron. In two subsequent chapters, we will consider the more
detailed energy-level structure of hydrogen, including fine structure,
the Lamb shift, and effects of the nucleus (hyperfine structure) and
of external magnetic and electric fields.
The hydrogen atom has played a special role in physics. Dan Kleppner eloquently describes this role in a
column in Physics Today
which starts with the sentence "To understand hydrogen is to understand all of physics". In this section we will unravel a lot of physics using the hydrogen atom - but we also include the helium atom to introduce new phenomena related to the presence of two electrons.
Hydrogen Atom
Bohr's Postulates
We briefly review the Bohr atom-- a model that was soon obsolete, but which
nevertheless provided the major impetus for developing quantum
mechanics. Balmer's empirical formula of 1885 had reproduced Angstrom's
observations of spectral lines in hydrogen to 0.1 Å accuracy,
but it was not until 1913 that Bohr gave an explanation for this
based on a quantized mechanical model of the atom. This model
involved the postulates of the Bohr Atom:
- Electron and proton are point charges whose interaction is coulombic at all distances.
- Electron moves in circular orbit about the center of mass in stationary states with orbital angular momentum
 .
.
These two postulates give the energy levels:

- One quantum of radiation is emitted when the system changes between these energy levels.
- The wave number of the radiation is given by the energy difference between the two levels:

Note that the wave number is a spectroscopic unit defined as the number of wavelengths per cm,  =
=  . It is important not to confuse the wave number with the magnitude of the wave vector
. It is important not to confuse the wave number with the magnitude of the wave vector  which defines a traveling wave of the form exp
which defines a traveling wave of the form exp . The magnitude of the wave vector is
. The magnitude of the wave vector is  times the wave number.
times the wave number.
The mechanical spirit of the Bohr atom was extended by Sommerfeld
in 1916 using the Wilson-Sommerfeld quantization rule (valid in the JWKB approximation),

where  and
and  are conjugate coordinate and momentum pairs
for each degree of freedom of the system. This extension yielded
elliptical orbits which were found to have an energy nearly
degenerate with respect to the orbital angular momentum for a
particular principal quantum number
are conjugate coordinate and momentum pairs
for each degree of freedom of the system. This extension yielded
elliptical orbits which were found to have an energy nearly
degenerate with respect to the orbital angular momentum for a
particular principal quantum number  . The degeneracy was
lifted by a relativistic correction whose splitting was in
agreement with the observed fine structure of hydrogen. (This was a great
cruel coincidence in physics. The mechanical description ultimately
had to be completely abandoned, in spite of the excellent agreement of theory
and experiment.) Although triumphant in hydrogen, simple mechanical models of helium or other two-electron
atoms failed, and real progress in understanding atoms
had to await the development of quantum mechanics.
. The degeneracy was
lifted by a relativistic correction whose splitting was in
agreement with the observed fine structure of hydrogen. (This was a great
cruel coincidence in physics. The mechanical description ultimately
had to be completely abandoned, in spite of the excellent agreement of theory
and experiment.) Although triumphant in hydrogen, simple mechanical models of helium or other two-electron
atoms failed, and real progress in understanding atoms
had to await the development of quantum mechanics.
Solution of Schrodinger Equation: Key Results
As you will recall from introductory quantum mechanics, the Schrodinger equation

can be solved exactly for the Coulomb Hamiltonian

by separation of variables

Summary of important results
Here, we highlight some important results:
 , just as in the Bohr model
, just as in the Bohr model![{\displaystyle \langle r_{n\ell }\rangle ={\frac {n^{2}a_{0}}{Z}}\{1+{\frac {1}{2}}[1-{\frac {\ell (\ell +1)}{n^{2}}}]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20007b307fe177b643a0543125ed8e7e90ff24e1)

Here,  is the Rydberg constant and
is the Rydberg constant and  , where
, where  is the effective mass.
Note that the relation
is the effective mass.
Note that the relation

follows directly from the Virial Theorem, which states in general that  For a spherically symmetric potential of the form
For a spherically symmetric potential of the form  , we have
, we have  and for the special case of the Coulomb potential
and for the special case of the Coulomb potential

(Note: In addition to the important case of the Coulomb potential, it is worth remembering the Virial Theorem for the harmonic oscillator,  .)
.)
The same factor of  from the Virial Theorem appears in the relationship between the Rydberg constant and the atomic unit of energy, the hartree:
from the Virial Theorem appears in the relationship between the Rydberg constant and the atomic unit of energy, the hartree:

We are working here in cgs units because the expressions are more concise in cgs than in SI. To convert to SI, simply make the replacement  .
.
Probability density of electron wavefunction at origin
Question: How does the density  of an
of an  -electron
at the origin depend on
-electron
at the origin depend on  and
and  ?
?
- A.

- B.

- C.

- D.

The exact result for the density at the origin is  (C). To arrive at the
(C). To arrive at the  scaling, we observe that the
scaling, we observe that the  and
and  only appear in the Hamiltonian in the combination
only appear in the Hamiltonian in the combination  . Thus, any result for hydrogen can be extended to the case of nuclear charge
. Thus, any result for hydrogen can be extended to the case of nuclear charge  simply by making the substiution
simply by making the substiution  . This leads, in turn, to the substitutions
. This leads, in turn, to the substitutions

Thus, the density  , so the answer can only be A or C.
It is tempting to assume that the
, so the answer can only be A or C.
It is tempting to assume that the  scaling can be derived from the length scale
scaling can be derived from the length scale  . However, the characteristic length
. However, the characteristic length  for the density at the origin is that which appears in the exponential term of the wavefunction
for the density at the origin is that which appears in the exponential term of the wavefunction  ,
,

Thus,

for all  . Remember this scaling, as it will be important for understanding such effects as the quantum defect in atoms with core electrons and hyperfine structure.
. Remember this scaling, as it will be important for understanding such effects as the quantum defect in atoms with core electrons and hyperfine structure.
Probability density near origin
For the case of  ,
,  has a node at
has a node at  , but the density near the origin is nonetheless of interest. It can be shown (Landau III, Chapter 36 .[1]) that, for small
, but the density near the origin is nonetheless of interest. It can be shown (Landau III, Chapter 36 .[1]) that, for small  ,
,

Since  , the density near the origin scales for large
, the density near the origin scales for large  as
as

References
Template:Reflist
Atomic Units
The natural units for describing atomic systems are obtained by setting to unity
the three fundamental constants that appear in the hydrogen Hamiltonian,  . One thus arrives at atomic units, such as
. One thus arrives at atomic units, such as
- length: Bohr radius =

- energy: 1 hartree =

- velocity:

- electric field:

- Note: This is the characteristic value for the
 orbit of hydrogen.
orbit of hydrogen.
As we see above, we can express atomic units in terms of  instead of
instead of  by introducing a single dimensionless constant
by introducing a single dimensionless constant

The fine structure constant  obtained its name from the appearance of
obtained its name from the appearance of  in the ratio of fine structure splitting to the Rydberg; it is the only fundamental constant in atomic physics. As such, it should ultimately be predicted by a complete theory of physics. Whereas precision measurements of other constants are made in atomic physics for purely metrological purposes ,
in the ratio of fine structure splitting to the Rydberg; it is the only fundamental constant in atomic physics. As such, it should ultimately be predicted by a complete theory of physics. Whereas precision measurements of other constants are made in atomic physics for purely metrological purposes ,  , as a dimensionless constant, is not defined by metrology. Rather,
, as a dimensionless constant, is not defined by metrology. Rather,  characterizes the strength of the electromagnetic interaction, as the following example will illustrate.
If energy uncertainties become become as large as
characterizes the strength of the electromagnetic interaction, as the following example will illustrate.
If energy uncertainties become become as large as  , the concept of a particle breaks down. This upper bound on the energy uncertainty gives us, via the Heisenberg Uncertainty Principle, a lower bound on the length scale within which an electron can be localized (before e.g. spontaneous pair production may occur)
, the concept of a particle breaks down. This upper bound on the energy uncertainty gives us, via the Heisenberg Uncertainty Principle, a lower bound on the length scale within which an electron can be localized (before e.g. spontaneous pair production may occur)

 Even at this short distance of
Even at this short distance of  , the Coulumb
interaction---while stronger than that in hydrogen at distance
, the Coulumb
interaction---while stronger than that in hydrogen at distance  --- is
only:
--- is
only:

i.e. in relativistic units the strength of this "stronger" Coulomb
interaction is  . The fact that
. The fact that  implies that the
Coulomb interaction is weak.
implies that the
Coulomb interaction is weak.
One-Electron Atoms with Cores
One-electron atom with core of net charge Z.
Question: Consider now an atom with one valence electron of principal quantum number  outside a core (comprising the nucleus and filled shells of electrons) of net charge
outside a core (comprising the nucleus and filled shells of electrons) of net charge  . Which of the following forms describes the lowest order correction to the hydrogenic energy
. Which of the following forms describes the lowest order correction to the hydrogenic energy  ?
?
- A.

- B.

- C.

- D.

Both C and D are correct answers, equivalent to lowest order in  . This scaling can be derived via perturbation theory. In particular, we can model the atom with a core of net charge
. This scaling can be derived via perturbation theory. In particular, we can model the atom with a core of net charge  as a hydrogenic atom with nuclear charge
as a hydrogenic atom with nuclear charge  ---described by Hamiltonian
---described by Hamiltonian  ---and add a perturbing Hamiltonian
---and add a perturbing Hamiltonian  to account for the penetration of the valence electron into the core.
As we showed before,
to account for the penetration of the valence electron into the core.
As we showed before,  . Thus, for the Hamiltonian
. Thus, for the Hamiltonian

where the penetration correction  is localized around
is localized around  , the deviation from hydrogenic energy levels
, the deviation from hydrogenic energy levels  is
is

where the proportionality constant depends on  . In particular, we can define the quantum defect
. In particular, we can define the quantum defect  such that
such that

The energy levels then take the form

This accounts for phenomenological formula for term values in the Balmer-Ritz formula,

This formula, in which the  are non-integers but are spaced by integer differences, had been deduced spectroscopically long before it could be understood quantum mechanically. It is possible to derive the quantum defect based on solving the radial Schrodinger equation in the JWKB approximation, which sheds light on the relation of the quantum defect to the phase shift of an electron scattering off a modified Coulomb potential; and for a sample calculation of the quantum defect for a model atom.
are non-integers but are spaced by integer differences, had been deduced spectroscopically long before it could be understood quantum mechanically. It is possible to derive the quantum defect based on solving the radial Schrodinger equation in the JWKB approximation, which sheds light on the relation of the quantum defect to the phase shift of an electron scattering off a modified Coulomb potential; and for a sample calculation of the quantum defect for a model atom.
Spectroscopic Notation
Neutral atoms consist of a heavy nucleus with charge  surrounded by
surrounded by  electrons. Positively charged atomic ions
generally have structure similar to the atom with the same number
of electrons except for a scale factor; negative ions lack the
attractive Coulomb interaction at large electron-core separation
and hence have few if any bound levels. Thus the essential
feature of an atom is its number of electrons, and their mutual
arrangement as expressed in the quantum
numbers.
An isolated atom has two good angular momentum quantum numbers,
electrons. Positively charged atomic ions
generally have structure similar to the atom with the same number
of electrons except for a scale factor; negative ions lack the
attractive Coulomb interaction at large electron-core separation
and hence have few if any bound levels. Thus the essential
feature of an atom is its number of electrons, and their mutual
arrangement as expressed in the quantum
numbers.
An isolated atom has two good angular momentum quantum numbers,
 and
and  . (This is strictly true only for atoms whose nuclei
have spin
. (This is strictly true only for atoms whose nuclei
have spin  . However,
. However,  is never significantly affected
by coupling to
is never significantly affected
by coupling to  in ground state atoms.) In zero external field
the atomic Hamiltonian possesses rotational invariance which
implies that each
in ground state atoms.) In zero external field
the atomic Hamiltonian possesses rotational invariance which
implies that each  level is degenerate with respect to the
level is degenerate with respect to the  states with specific
states with specific  (traditional atomic
spectroscopists call these states "sublevels"). For each
(traditional atomic
spectroscopists call these states "sublevels"). For each
 ,
, an atom will typically have a large number of discrete
energy levels (plus a continuum) which may be
labeled by other quantum numbers.
If Russell-Saunders coupling (
an atom will typically have a large number of discrete
energy levels (plus a continuum) which may be
labeled by other quantum numbers.
If Russell-Saunders coupling ( coupling) is a good description of the atom (true for light atoms), then
coupling) is a good description of the atom (true for light atoms), then  and
and  , where
, where


are nearly good quantum numbers and may be used to distinguish the
levels. In this case the level is designated by a Term
symbolized  where
where  and
and  are written
numerically and
are written
numerically and  is designated with this letter code:
is designated with this letter code:
|
| |  : : | O | 1 | 2 | 3 | 4 | ... |
|
| | Letter: |  |  |  |  |  |
The Letters stand for Sharp, Principal, Diffuse, and Fundamental -
adjectives applying to the spectral lines of one electron atoms.
When describing a hydrogenic atom, the term is preceded by the principle quantum number of the
outermost electron. For example, in sodium, the ground state is designated  , while the D-line excited states are
, while the D-line excited states are  and
and  .
This discussion of the term symbol has been based on quantum numbers for all electrons of the atom. Alternatively one may have or assume
knowledge of the internal structure - the quantum numbers of each
electron. These are specified as the configuration, e.g..
.
This discussion of the term symbol has been based on quantum numbers for all electrons of the atom. Alternatively one may have or assume
knowledge of the internal structure - the quantum numbers of each
electron. These are specified as the configuration, e.g..

a product of symbols of the form  which represents
which represents  electrons in the orbital
electrons in the orbital  ,
,  .
.  is the principal
quantum number, which characterizes the radial motion and has the
largest influence on the energy.
is the principal
quantum number, which characterizes the radial motion and has the
largest influence on the energy.  and
and  are written
numerically, but the
are written
numerically, but the  ... coding is used for
... coding is used for  . Returning to the example of sodium, the configuration is
. Returning to the example of sodium, the configuration is
 , which is often abbrevated to simply
, which is often abbrevated to simply  .
In classifying levels, the term is generally more important
that the configuration because it determines the behavior of an
atom when it interacts with
.
In classifying levels, the term is generally more important
that the configuration because it determines the behavior of an
atom when it interacts with  or
or  fields. Selection
rules, for instance, generally deal with
fields. Selection
rules, for instance, generally deal with  ,
,  ,
,  . Furthermore the
configuration may not be pure - if two configurations give rise
to the same term (and have the same parity) then intra-atomic
electrostatic interactions can mix them together. This process,
called configuration interaction, results in shifts in the level
positions and intensities of special lines involving them as well
as in correlations in the motions of the electrons within the
atoms.
. Furthermore the
configuration may not be pure - if two configurations give rise
to the same term (and have the same parity) then intra-atomic
electrostatic interactions can mix them together. This process,
called configuration interaction, results in shifts in the level
positions and intensities of special lines involving them as well
as in correlations in the motions of the electrons within the
atoms.
Energy Levels of Helium
<figure id="he_levels" noautocaption>
Figure %i. Energy levels of helium. Figure adapted from Gasiorowicz. [2] The quantum mechanics texts of Gasiorowicz and Cohen-Tannoudji [3] are valuable resources for more detailed treatment of the helium atom. </figure>
If we naively estimate the binding energy of ground-state helium ( ) as twice the binding energy of a a single electron in a hydrogenic atom with
) as twice the binding energy of a a single electron in a hydrogenic atom with  , we obtain
, we obtain  . Comparing to the experimental result of 79 eV, we see a big (39 eV) discrepancy. However, we have neglected the
. Comparing to the experimental result of 79 eV, we see a big (39 eV) discrepancy. However, we have neglected the  interaction. Introducing a perturbation operator
interaction. Introducing a perturbation operator

where  is the distance between the two electrons, and still approximating each electron to be in the
is the distance between the two electrons, and still approximating each electron to be in the  state---yielding a total wavefunction
state---yielding a total wavefunction  ---we obtain the first-order correction
---we obtain the first-order correction

which removes most of the discrepancy. A single-parameter variational ansatz using  as parameter removes
as parameter removes  of the remaining discrepancy. Thus, although we cannot solve the helium Hamiltonian exactly, we can understand the ground-state energy well simply by taking into account the shielding of the nuclear charge by the
of the remaining discrepancy. Thus, although we cannot solve the helium Hamiltonian exactly, we can understand the ground-state energy well simply by taking into account the shielding of the nuclear charge by the  interaction.
For the first excited states, there are two possible electronic configurations,
interaction.
For the first excited states, there are two possible electronic configurations,  and
and  . The
. The  electron sees a shielded nucleus (He
electron sees a shielded nucleus (He vs. He
vs. He ) due to the
) due to the  electron, and consequently has a smaller binding energy, comparable to the
electron, and consequently has a smaller binding energy, comparable to the  binding energy for hydrogen (
binding energy for hydrogen ( eV). For the
eV). For the  electron, which has no node at the nucleus, the shielding effect is similar but weaker (see <xr id="he_levels" />). Consider now the possible terms for the
electron, which has no node at the nucleus, the shielding effect is similar but weaker (see <xr id="he_levels" />). Consider now the possible terms for the  configuration:
configuration:
 (singlet)
(singlet) (triplet)
(triplet)
The singlet and triplet states are, respectively, antisymmetric and symmetric under particle exchange. Since Fermi statistics demand that the total wavefunction of the electrons be antisymmetric, the spatial and spin wavefunctions must have opposite symmetry,

Here,  is the wavefunction with symmetric spatial part and antisymmetric spin state
is the wavefunction with symmetric spatial part and antisymmetric spin state  , i.e. the spin singlet (S=0,
, i.e. the spin singlet (S=0,  term).
term).  is the wavefunction with antisymmetric spatial part and symmetric spin state
is the wavefunction with antisymmetric spatial part and symmetric spin state  , i.e. the spin triplet (S=1,
, i.e. the spin triplet (S=1,  term).
Now consider the Coulomb energy
term).
Now consider the Coulomb energy  of the
of the  interaction in these excited states:
interaction in these excited states:
![{\displaystyle {\begin{aligned}\Delta E&={\frac {1}{2}}\int \int {\frac {e^{2}}{r_{12}}}[|\psi _{100}(r_{1})|^{2}|\psi _{200}(r_{2})|^{2}+(r_{1}\leftrightarrow r_{2})]\\&\pm {\frac {1}{2}}\int \int {\frac {e^{2}}{r_{12}}}[\psi _{100}^{*}(r_{1})\psi _{200}^{*}(r_{2})\psi _{100}(r_{2})\psi _{200}(r_{1})+(r_{1}\leftrightarrow r_{2})]\\&=\Delta E^{Coul}\pm \Delta E^{exch}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f7da0a65ae741e23636787881de55fc50acbe4a)
The first term (called the Coulomb term, although both terms are Coulombic in origin) is precisely what we would calculate classically for the repulsion between two electron clouds of densities  and
and  . The second term, the exchange term, is a purely quantum mechanical effect associated with the Pauli exclusion principle.
The triplet state has lower energy, because the antisymmetric spatial wavefuntion reduces
. The second term, the exchange term, is a purely quantum mechanical effect associated with the Pauli exclusion principle.
The triplet state has lower energy, because the antisymmetric spatial wavefuntion reduces  repulsion interactions. Since the interaction energy is spin-dependent, it can be written in the same form as a ferromagnetic spin-spin interaction,
repulsion interactions. Since the interaction energy is spin-dependent, it can be written in the same form as a ferromagnetic spin-spin interaction,
<equation id="ferro" noautocaption>
(%i)

</equation>
To see this, we use the relation  . Since
. Since  , <xr id="ferro"/> is equivalent to
, <xr id="ferro"/> is equivalent to

where we have substituted  for the singlet and triplet states, respectively. Bear in mind that, although the interaction energy is spin-dependent, the origin of the coupling is electrostatic and not magnetic. Because of its electrostatic origin, the exchange energy (0.8 eV for the
for the singlet and triplet states, respectively. Bear in mind that, although the interaction energy is spin-dependent, the origin of the coupling is electrostatic and not magnetic. Because of its electrostatic origin, the exchange energy (0.8 eV for the  splitting, as indicated in <xr id="he_levels" />) is much larger than a magnetic effect such as the fine structure splitting, which carries an extra factor of
splitting, as indicated in <xr id="he_levels" />) is much larger than a magnetic effect such as the fine structure splitting, which carries an extra factor of  .
.
Dipole-allowed transitions (solid) and intercombination lines (dashed) in helium.
What field (coupling) drives singlet-triplet transitions?
A. Optical fields (dipole operator)
B. rotating magnetic fields
C. Both
D. None
Singlet-triplet transitions are forbidden by the  selection rule, so to first order the answer is D. A is ruled out because the dipole operator acts on the spatial wavefunction, not on the spin part. One might think (B) that a transverse magnetic field, which couples to
selection rule, so to first order the answer is D. A is ruled out because the dipole operator acts on the spatial wavefunction, not on the spin part. One might think (B) that a transverse magnetic field, which couples to  ,
,  ,
,  , can be used to flip a spin. However, a transverse
, can be used to flip a spin. However, a transverse  field can only rotate the two spins together; it cannot rotate one spin relative to the other, as would be necessary to change the magnitude of
field can only rotate the two spins together; it cannot rotate one spin relative to the other, as would be necessary to change the magnitude of  . Because all spin operators are symmetric against particle exchange, they couple only
. Because all spin operators are symmetric against particle exchange, they couple only  . Thus, spatial and spin symmetry (S,A) are both good quantum numbers.
More formally, all observables
. Thus, spatial and spin symmetry (S,A) are both good quantum numbers.
More formally, all observables  commute with the particle exchange operator
commute with the particle exchange operator ![{\displaystyle [P_{ij},{\hat {O}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d769b158d5a631785fbe3e4a49023eeb2ea0cabd) , and
, and  (S or A) is a good quantum number. Thus, as long as wavefunction and operators separate into spin dependent and space dependent parts
(S or A) is a good quantum number. Thus, as long as wavefunction and operators separate into spin dependent and space dependent parts  , both
, both  's are conserved. Intercombination (i.e. transition between singlet and triplet) is only possible when this assumption is violated, i.e. when the spin and spatial wavefunctions are mixed, e.g. by spin orbit coupling.
As we will see later on, spin orbit coupling is
's are conserved. Intercombination (i.e. transition between singlet and triplet) is only possible when this assumption is violated, i.e. when the spin and spatial wavefunctions are mixed, e.g. by spin orbit coupling.
As we will see later on, spin orbit coupling is  , and hence is weak for helium. Thus, the
, and hence is weak for helium. Thus, the  state of helium is very long-lived, with a lifetime of about 8,000 s. Historically, the absence of transition between singlet and triplet states led to the belief that there were two kinds of helium, ortho-helium (triplet) and para-helium (singlet).
state of helium is very long-lived, with a lifetime of about 8,000 s. Historically, the absence of transition between singlet and triplet states led to the belief that there were two kinds of helium, ortho-helium (triplet) and para-helium (singlet).
The other noble gases (Ne, Ar, Kr, Xe) have lifetimes on the order of 40 s.
Because they are so narrow, intercombination lines are of great interest for application in optical clocks. While a lifetime of 8000 s is too long to be useful (because such a narrow transition is difficult both to find and to drive), intercombination lines in Mg, Ca, or Sr---with linewidths ranging from mHz to kHz---are discussed as potential optical frequency standards. [4] [5]
How can you measure an 8000 s lifetime? Well, definitely not by observing the decay of the excited state over 8000 s since collisions and other effects will shorten the lifetime. However, if you measure the rate of emitted XUV photons and the number of atoms in the emitting state, you get the lifetime. Absolute measurements of these numbers are difficult, and therefore the accuracy for the lifetime will not be high. A very elegant method has been recently applied to metastable helium.[6] While recording the XUV photon rate, the atoms in the  state are strongly driven to the
state are strongly driven to the  state, saturating the transition, putting half of the atoms into the
state, saturating the transition, putting half of the atoms into the  state which has a known (and more easily measured) lifetime of 5.7 ms. The XUV rate jumps up by a factor of about a million which is half the ratio of the lifetimes of the two states.
state which has a known (and more easily measured) lifetime of 5.7 ms. The XUV rate jumps up by a factor of about a million which is half the ratio of the lifetimes of the two states.
References
Template:Reflist
Appendix: Solution of the Schrodinger Equation
See Solution of the Schrodinger Equation for an Atom
Appendix: More on the Quantum Defect
See More on the Quantum Defect
Appendix: Metrology and Precision Measurement and Units
See Metrology and Precision Measurement and Units
References
- CohenT: Claude Cohen-Tannoudji, Bernard Diu, and Franck Laloë. Quantum Mechanics. Hermann, Paris, 1977.
- Freeman1976: Richard R. Freeman and Daniel Kleppner. Core polarization and quantum defects in high-angular-momentum states of alkali atoms. Phys. Rev. A, 14(5):1614–1619, Nov 1976.
- Gasiorowicz: Stephen Gasiorowicz. Quantum Physics. Wiley, 2003.
- Landau: L. D. Landau and L. M. Lifshitz. Quantum Mechanics: Non-Relativistic Theory. Elsevier Science, 1977.
- Ludlow2006: A. D. Ludlow, M. M. Boyd, T. Zelevinsky, S. M. Foreman, S. Blatt, M. Notcutt, T Ido, and J. Ye. Systematic study of the sr-87 clock transition in an optical lattice. Physical Review Letters, 96(3):033003, 2006.
- Ludlow2008: A. D. Ludlow, T. Zelevinsky, G. K. Campbell, S. Blatt, M. M. Boyd, M. H. G. de Miranda, M. J. Martin, J. W. Thomsen, S. M. Foreman, Jun Ye, T. M. Fortier, J. E. Stalnaker, S. A. Diddams, Y. Le Coq, Z. W. Barber, N. Poli, N. D. Lemke, K. M. Beck, and C. W. Oates. Sr lattice clock at
 fractional uncertainty by remote optical evaluation with a ca clock. Science, page 1153341, 2008.
fractional uncertainty by remote optical evaluation with a ca clock. Science, page 1153341, 2008.
- codata2002: Peter J. Mohr, Barry N. Taylor, and David B. Newell. CODATA recommended values of the fundamental physical constants: 2002. Rev. Mod. Phys., 77, Jan 2005. Available online at <url>
</url>http://physics.nist.gov/constants.
- Parsons1967: R. G. Parsons and V. F. Weisskopf. Z. Phys., 202:492, 1967.
- Seaton1966: M. J. Seaton. Proc. Phys. Soc., 88:801, 1966.
- Hodgman2009: S.S. Hodgman, R.G. Dall, L.J. Byron, K.G.H. Baldwin, S.J. Buckman, and A.G. Truscott. Phys. Rev. Lett., 103:053002, 2009.
- ↑ Landau: L. D. Landau and L. M. Lifshitz. Quantum Mechanics: Non-Relativistic Theory. Elsevier Science, 1977
- ↑ Stephen Gasiorowicz. Quantum Physics. Wiley, 2003
- ↑ Claude Cohen-Tannoudji, Bernard Diu, and Franck Laloë. Quantum Mechanics. Hermann, Paris, 1977
- ↑ A. D. Ludlow, T. Zelevinsky, G. K. Campbell, S. Blatt, M. M. Boyd, M. H. G. de Miranda, M. J. Martin, J. W. Thomsen, S. M. Foreman, Jun Ye, T. M. Fortier, J. E. Stalnaker, S. A. Diddams, Y. Le Coq, Z. W. Barber, N. Poli, N. D. Lemke, K. M. Beck, and C. W. Oates. Sr lattice clock at 1×10−16 fractional uncertainty by remote optical evaluation with a ca clock. Science, page 1153341, 2008.
- ↑ A. D. Ludlow, M. M. Boyd, T. Zelevinsky, S. M. Foreman, S. Blatt, M. Notcutt, T Ido, and J. Ye. Systematic study of the sr-87 clock transition in an optical lattice. Physical Review Letters, 96(3):033003, 2006.
- ↑ S.S. Hodgman, R.G. Dall, L.J. Byron, K.G.H. Baldwin, S.J. Buckman, and A.G. Truscott. Phys. Rev. Lett., 103:053002, 2009.
















![{\displaystyle \langle r_{n\ell }\rangle ={\frac {n^{2}a_{0}}{Z}}\{1+{\frac {1}{2}}[1-{\frac {\ell (\ell +1)}{n^{2}}}]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20007b307fe177b643a0543125ed8e7e90ff24e1)







































































































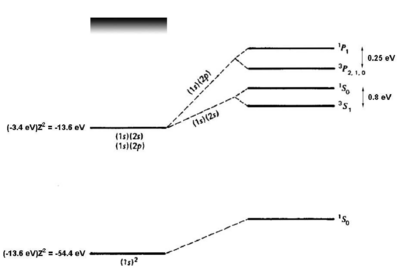




























![{\displaystyle {\begin{aligned}\Delta E&={\frac {1}{2}}\int \int {\frac {e^{2}}{r_{12}}}[|\psi _{100}(r_{1})|^{2}|\psi _{200}(r_{2})|^{2}+(r_{1}\leftrightarrow r_{2})]\\&\pm {\frac {1}{2}}\int \int {\frac {e^{2}}{r_{12}}}[\psi _{100}^{*}(r_{1})\psi _{200}^{*}(r_{2})\psi _{100}(r_{2})\psi _{200}(r_{1})+(r_{1}\leftrightarrow r_{2})]\\&=\Delta E^{Coul}\pm \Delta E^{exch}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f7da0a65ae741e23636787881de55fc50acbe4a)








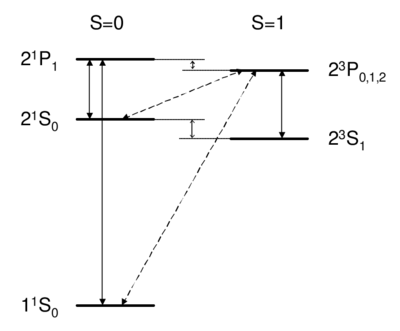







![{\displaystyle [P_{ij},{\hat {O}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d769b158d5a631785fbe3e4a49023eeb2ea0cabd)





