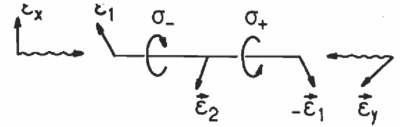Sub-Doppler cooling

The general laser cooling methods we have seen so far may be conceptually understood using the physics of optical pumping. However, traditional laser cooling methods do not allow the cooling to temperatures below a certain limit, known as the single photon recoil limit. Nevertheless, by generalizing laser cooling methods beyond two-level approximations, and by considering other degrees of freedom such as laser polarization, sub-Doppler temperatures can be achieved, as we see below.

Cooling as optical pumping

Let us begin by generalizing what we have discussed in terms of light forces and cooling, by saying that in some sense, all cooling processes can be related to a process known as optical pumping.

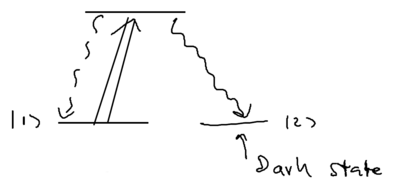
Optical pumping can be understood through the following scenario:

If level $|2{\rangle }$ is a dark state, meaning that no optical transitions occur from it, then eventually light incident on all the other (optically accessible) transitions will pump all the atoms into that dark state.

What does optical pumping have to do with cooling? Consider this scenario:

Now write down the populations of the two levels,

${\frac {n_{2}}{n_{1}}}=e^{-\beta \Delta E}$

and clearly as $n_{2}\rightarrow 0$, then the effective temperature of the system goes to zero.

This picture can be used to understand laser cooling, by thinking of cooling as optical pumping of motional states of the atom. For example, beam cooling was optical pumping into dark states of velocity.

On the other hand, laser cooling, is not just about reaching a specific internal atomic state, but rather, external states representing momenta of the atoms. Typically, internal states such as hyperfine states do not couple well to eternal degrees of motion, so internal state cooling does not generally work well to cool the motion of atoms.

We will now encounter optical pumping in two different scenarios.

Sub-Doppler cooling

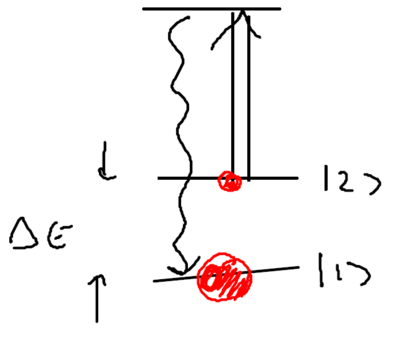
The main new feature which allows cooling to beyond the photon recoil temperature is the use of multiple energy levels in laser cooling. Consider this energy level configuration, with multiple levels in the ground state:

This allows Raman resonances to be created in the ground state, which can be extremely narrow. The decay of the states coupled by a Raman transition can be expressed as

$\Gamma '={\frac {1}{\tau _{p}}}={\frac {\Omega ^{2}}{\delta ^{2}}}\Gamma \,,$

where $\delta$ is the detuning from the virtual upper state, $\Gamma$ is the (short) lifetime of the upper state, and $\Omega$ is the Rabi frequency.

When there are long internal relaxation times, it is important that these timescales are taken into account in the cooling process. In particular, such long timescales allows for large time-lags, and recall that large time-lags gave rise to high cooling rates in our dressed atom picture of laser cooling. In particular, we found that the populations of the states, under laser cooling, behave as

$\pi ({\vec {x}})=\pi _{e}({\vec {x}}-v\tau _{relax})\,,$

so that long lifetimes lead to very strong laser cooling.

Often, the final temperature of schemes with narrow resonances lead to

$k_{B}T_{\rm {final}}\propto \hbar \Gamma '\,,$

because of the physical intuition that narrower resonances give higher resolution in distinguishing velocity classes of moving atoms. Thus, in this picture, the Doppler temperature limit is $T_{final}\sim \Gamma$. More precisely, for Raman cooling, it turns out to be

$T_{final}\sim \Gamma '{\frac {\Gamma }{\delta }}\,.$

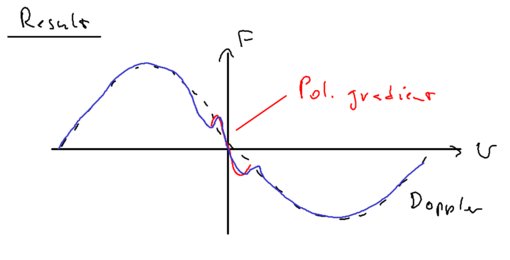
With ground state resonances, provided in this optical pumping picture, features arise in the plot of force verses velocity which are very narrow:

This gives a wide feature which provides a large capture range, and a narrow middle feature which leads to high cooling rates. This is the result of a specific sub-doppler cooling technique known as polarization gradient cooling, as we see next.

Polarization gradient cooling

The following is an iconic picture of polarization gradient cooling. If you have just a two-level atom, it doesn't care what the polarization is. But if you have internal levels such as in the example above, the atoms do care about the incident polarization. Shown here is a configuration in which the change of relative phases of the two counter-propagating lasers lead to a gradient in which the polarization changes from circular to linear, to opposite circular, to opposite linear:

(figure from Dalibard and Cohen-Tannoudji, {\em Laser cooling below the Doppler limit by polarization gradients: simple theoretical models, JOSAB, p2023})

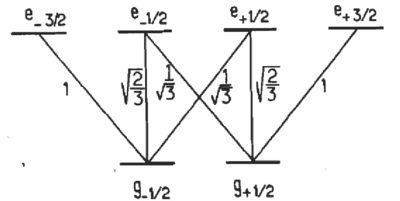
Polarization gradient cooling is best explained using a picture of the different Clebsch-Gordan coefficients for the transition rates (these sample rates given for a $J_{g}=1/2\leftrightarrow J_{e}=3/2$ transition):

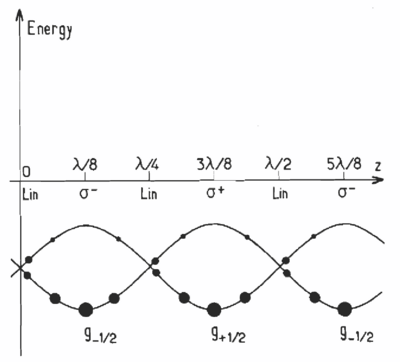
The strongest transitions are those on the ends. $\sigma ^{+}$ light moves the state to the right, and has a stronger AC Stark shift. $\sigma ^{-}$ light does correspondingly to the transition on the left. This results in a periodic potential in space:

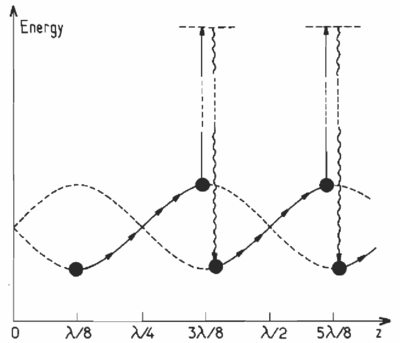
The steady state populations are represented by filled circles for a $J_{g}=1/2$ ground state in the lin $\perp$ lin configuration of light polarizations, and for negative detuning. This results in atoms having to climb potential hills more often than descending hills, leading to an energy loss mechanism of this form:

assuming the polarization changes between linear, $\sigma ^{-}$, linear, and $\sigma ^{+}$ from left to right.

This is a Sisyphus cooling mechanism, as was described previously in the context of blue detuned optical molasses. Here the Sisyphus cooling is no longer between dressed states, but rather, between hyperfine states of the atom. Historically, it is in this context that Sisyphus cooling became important.

Sub-recoil cooling

Sub-recoil cooling means that the residual thermal velocity of the cooled atom is less than that due to the momentum of emitted photons. For a long time, it was believed that laser cooling could not achieve temperatures below this photon recoil limit.

Let us begin by motivating the discussion with a "proof" that sub-recoil cooling is not possible. We may calculate the change of energy in an absorption + spontaneous emission cycle. We first have kinetic energy $m{\vec {v}}^{2}/2$. After absorption, the energy is

${\frac {1}{2}}\left({m{\vec {v}}+\hbar {\vec {k}}_{L}}\right)^{2}\,,$

After emission, the energy is

${\frac {1}{2}}\left({m{\vec {v}}+\hbar {\vec {k}}_{L}-\hbar {\vec {k}}_{e}}\right)^{2}\,,$

where ${\vec {k}}_{e}$ is the emitted photon's wavevector. The energy change is thus

$\Delta E=2E_{rec}+\hbar ({\vec {k}}_{L}-{\vec {k}}_{e})\cdot {\vec {v}}\,.$

The average over several cycles gives a change in mechanical energy of the atom

${\overline {\Delta E}}=2E_{rec}+\hbar {\vec {k}}_{L}\cdot {\vec {v}}\,.$

To make this as negative as possible, a counter-propagating beam should be used (the laser beam should be anti-parallel to the velocity), giving

${\overline {\Delta E}}=2E_{rec}-\hbar k_{L}v\,,$

giving that cooling is possible only if (using the fact that $E_{rec}=k_{L}^{2}/m$) the

${\overline {\Delta E}}=2E_{rec}-\hbar k_{L}v<0\,,$

so that initial velocity must be

$v>v_{rec}={\frac {\hbar k_{L}}{m}}\,.$

Thus, the moment atoms reach the recoil velocity, atoms heat as much as they cool.

How can this limit be circumvented? Broadly speaking, spontaneous emission is necessary for cooling. Stimulated emission just swaps population from one state to another, and does not change the total system entropy.

The fact is that this limit can be circumvented if we do not treat $\Delta E$ using an average over cycles, and if we do not throw away the graininess of the cooling process. After all, sometimes, atoms can emit such that their final energy is zero. So the last scattered photon may not be random, if things are setup properly. We are jostling around the atoms with random photons, after all, so sometimes, an atom may drop to very low temperature. As an example, if the atoms are in a potential well which has a hole in the center, then atoms can get trapped in the hole, and reach very low temperatures.

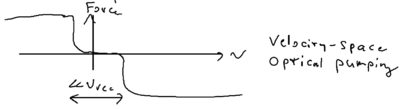
This concept is used in dark state cooling. Suppose the force as a function of velocity looks like:

This potential has an excitation that goes to zero at zero velocity. Essentially it is the picture of velocity space optical pumping. A variety of methods can realize such potentials, such as Raman excitations (Raman cooling), or velocity selective coherent population trapping (VSCPT), or electro-magnetically-induced transparency methods.

We will not describe these methods any further, however, because in practice, a different technique: evaporative cooling, has taken over the field, and has become the workhorse of low temperature atom cooling.

References

• Important paper: J. Dalibard and C. Cohen-Tannoudji, J. Opt. Soc. Am .B 2, 1707 (1985) Download