Dipole forces within the dressed atom approach

In this section, we visit the physics of stimulated light forces, using the the dressed atom picture. Just to whet your appetite for the following - we will understand, below, why it is blue detuned light you choose for laser cooling at high intensities, rather than red detuned light. Also, recall that in the case of the stimulated force, fluctuations of the stimulated force cause heating. There is a special nature to the fluctuations of the stimulated force, due to the radiative cascade picture in the dressed atom approach. In switching from one dressed level to the next, the force switches sign! The atom thus get kicked back and forth. We will therefore see how these fluctuations of the stimulated force lead to momentum diffusion. The stimulated force has application mostly to dipole traps and optical lattices. Understanding the cooling and heating due to the stimulated force really broadens your understanding of what light forces are about. It is essentially different from the spontaneous light force, involved in the optical molasses.

The insights from today will cover dipole traps, blue molasses, and heating from dipole forces.

Review of the dressed atom picture

Let us begin with a reminder about three things we need from the dressed atom picture: energy levels, populations, and relaxation times.

Energies

Recall that there is a splitting between dressed states, giving the energies

$\hbar \Omega (r)=\hbar {\sqrt {\Omega _{1}^{2}(r)+\delta _{L}^{2}}}\,.$

Populations

We also want to know the populations $\Pi _{1}$ and $\Pi _{2}$ of the dressed states $1$ and $2$; these came from diagonalizing the coupling matrices and introducing rate equations, giving

$\Pi _{1}^{st}={\frac {\sin ^{4}\theta }{\cos ^{4}\theta +\sin ^{4}\theta }}$

$\Pi _{2}^{st}={\frac {\cos ^{4}\theta }{\cos ^{4}\theta +\sin ^{4}\theta }}$

where $\tan 2\theta =-\Omega _{1}/\delta _{L}$.

Relaxation rates

Finally, recall that if we are not in steady state, there are relaxation rates involved which drive the system to the steady state. These rates are proportional to the spontaneous emission rate:

$\Gamma _{pop}=\Gamma (\cos ^{4}\theta +\sin ^{4}\theta )\,.$

Mean dipole force at zero velocity

Let us begin by considering what force is seen by an atom in a tightly focused laser beam, when the light is detuned to the red or to the blue of the atomic transition.

The dipole force

If you have a laser beam which is spatially focused, then the energy of the atom as a function of position is a function of where the atom is located relative to the beam:

Assume the light is intense, so that we may use the dressed atom picture. The splitting of the energies of the upper and lower dressed level leads to energies $\pm \hbar \Omega (r)/2$, so the forces seen by the upper and lower levels are

${\begin{aligned}F_{1}&=-{\frac {\hbar }{2}}\nabla \Omega (r)\\F_{2}&=+{\frac {\hbar }{2}}\nabla \Omega (r)\end{aligned}}$

Note that in these expressions, the Rabi frequency is a function of space, because of the spatial dependence of the light intensity. The average force is thus

${\begin{aligned}\langle F_{dip}\rangle &=F_{1}\Pi _{1}^{st}+F_{2}\Pi _{2}^{st}\\&=-{\frac {\hbar \delta _{L}}{2}}{\frac {\Omega _{1}^{2}}{{\frac {\Omega _{1}^{2}}{2}}+\delta _{L}^{2}}}{\vec {\alpha }}\end{aligned}}$

Note that this is only valid in several limits, imposed by the basic constraint that the dressed atom picture is valid (ie strong light intensity).

Dipole forces seen with blue and red detuned light

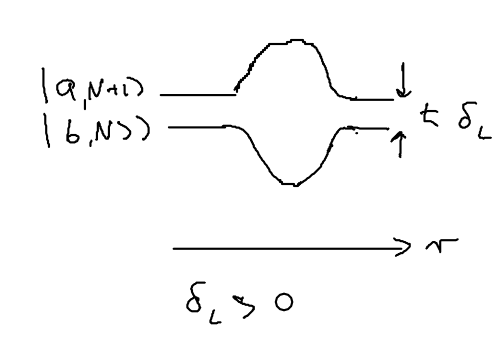
We may compare what happens when we have blue detuned light versus red detuned light. Consider two choices. What we couple with the light is the ground state with $N+1$ photons, $|a,N+1{\rangle }$, and the excited state, with $N$ photons, $|b,N{\rangle }$. Which of these two states have higher energy for positive (blue) detuning? The $|a,N+1{\rangle }$ state, because the photon has more energy than the atomic transition. Therefore, the proper labels on the energy levels when blue detuned are:

On the other hand, when red detuned, the energy levels should be labeled as:

Keep in mind, however, that spontaneous emission drives the atom towards its ground state. Eventually, therefore, in the blue detuned state the upper energy level eventually has more population, whereas when red detuned the lower energy level has more population.

The dipole force is repulsive for blue detuning, and the dipole force is attractive for red detuning.

What happens when we are on resonance, and the detuning is zero? In this case, the upper and lower states see equal force, so the average force is zero.

Mean dipole force at non-zero velocity

As a second application, let us discuss the mean dipole force seen by an atom which is not at rest, but is slowly moving. This will let us understand how blue detuned light cools an atom, in the dressed atom picture.

We have to go one step beyond what we did for the mean forces, because the derivations above stem from a picture of forces arising from a potential, and motion in a potential is conservative. Recall that the average force is

$\langle F_{dip}\rangle =F_{1}\Pi _{1}^{st}+F_{2}\Pi _{2}^{st}$

Now factor in the fact that the populations are not {\em instantaneously} in the steady state, but rather, there is a time lag of $1/\Gamma _{pop}$ before the populations come into equilibrium.

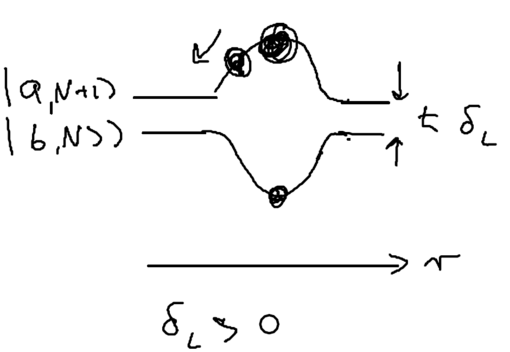
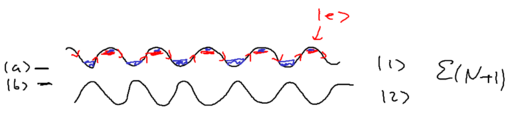
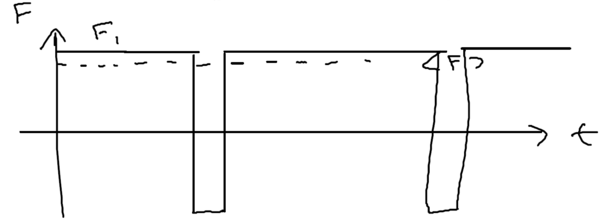
Consider the picture of an atom going through a laser beam; note that this could be a standing wave, as in an optical lattice. Let's figure out what the atom has to do as it traverses the beam. Originally, the atom is purely in the ground state, and at positive detuning the ground state is the upper energy level. To reach the top of the energy hump, there must be some admixture of the excited state added:

The size of the blobs in this picture reflect the population in the level. Assume the atom is moving towards the right. What is the extra force seen because the populations lag behind that which it should have in steady state, as the atom is moving? The more the population is in the upper level, the more force there is to the left. So if the actual population (dotted red lines) is larger than the steady state (solid lines) there is an extra force to the left.

As the atom leaves the middle of the beam, the populations continue to lag behind. But due to the population lag, the upper level population is a bit smaller than it would be in steady state. This causes the atoms to continue seeing a force to the left.

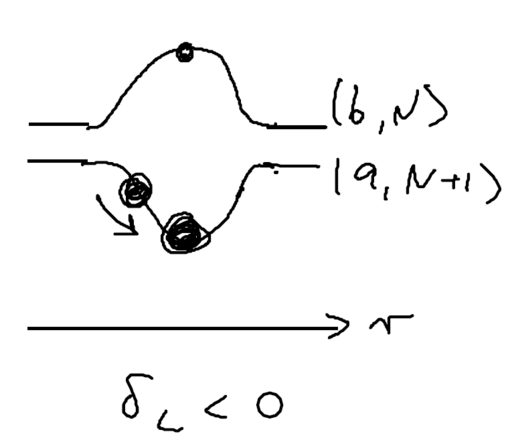
Now imaging that an atom rides a standing wave, going up and down. Because of the time lag in the population, the atoms now see a force in the opposite direction from its movement. Let us emphasize this point: the time lag leads to a hysteresis, which gives rise to dissipation.

More formally, the populations are the steady state values, but not at the present position of the atom, but rather, at a time given by ${\vec {v}}\tau _{pop}$ time before:

$\Pi _{i}=\Pi _{i}^{st}({\vec {r}}-{\vec {v}}\tau _{pop})\,.$

Thus, the dipole force as a function of position and velocity is

${\vec {F}}_{dip}({\vec {r}},v)={\vec {F}}_{dip}^{st}-{\frac {2\hbar \delta _{L}}{\Gamma }}\left({\frac {\Omega _{1}^{2}(r)}{\Omega _{1}^{2}(r)+2\delta _{L}^{2}}}\right)({\vec {\alpha }}\cdot {\vec {v}}){\vec {\alpha }}$

where ${\vec {F}}_{dip}^{st}$ is the force at $v=0$, and $\alpha$ is the friction coefficient obtained.

Now suppose the light is a one-dimensional standing wave $\Omega _{1}(x)=2\Omega _{1}\cos kx$. Averaging over one cycle of the standing wave, we find that the force seen by the atom is

$\langle F_{dip}\rangle =-\alpha v\,,$

noting that ${\vec {F}}_{dip}^{st}$ averages to zero.

Some limits of this behavior are very useful. In the limit of large detuning $\delta _{L}\gg \Omega _{1}$, in the standing wave case, we note that ${\vec {\alpha }}\approx {\vec {k}}$, so the friction coefficient in this situation is approximately

$\alpha \approx {\frac {\hbar \delta _{L}}{\Gamma }}{\frac {\Omega _{1}^{6}}{\delta _{L}^{6}}}k^{2}\,.$

This will be derived later, when we strip the dressed atom picture to its bare bones and look at it for physical insight.

Atomic momentum diffusion in the dressed atom picture

We've understood that the dynamics of the radiative cascade leads to population lag, which leads to dissipation. The next thing we want to discuss is that there is also a heating mechanism, which is due to fluctuating forces. Let us see how this arises in the dressed atom picture, for an atom in a standing wave.

Momentum diffusion from force fluctuations

Recall that in the molasses the final temperature was given by $\alpha /D_{p}$, where $\alpha$ was the friction force describing how well we cool, and $D_{p}$ was the momentum diffusion rate due to spontaneous emission. The momentum diffusion coefficient is

$2D_{p}={\frac {d}{dt}}\left(\langle p^{2}\rangle -\langle p{\rangle }^{2}\right)\,.$

Note that such diffusion arises from fluctuating forces. Physically, the momentum is the time integral of all the forces which have been acting on the particle. We can write $p^{2}$ as ${\vec {p}}\cdot {\vec {p}}$. Thus,

${\begin{aligned}2D_{p}&=2\langle {\vec {p}}\cdot {\vec {F}}(0)\rangle -{\langle }{\vec {p}}\rangle {\langle }{\vec {F}}(0){\rangle }\\&=2\int _{-\infty }^{0}\left({\langle }{\vec {F}}(t){\vec {F}}(0){\rangle }-{\langle }{\vec {F}}(t){\rangle }{\langle }{\vec {F}}(0)\rangle \right)dt\,.\end{aligned}}$

Thus, the momentum diffusion coefficient can be written as an integral over the force correlations:

${\begin{aligned}D_{p}&=\int _{0}^{\infty }\left({\langle }{\vec {F}}(t){\vec {F}}(0){\rangle }-{\langle }{\vec {F}}(0){\rangle }^{2}\right)dt\end{aligned}}$

When we discussed momentum diffusion from absorbed light, we had a clear picture of where randomness of momentum came from: the absorbed photons. In this case, we don't have such a clear picture in the absorbed momentum, but we have a clear picture of the forces experienced by the atom. It this thus useful to relate momentum diffusion to the randomness of forces experienced. We will then get a heating rate from

${\langle }{\dot {E}}_{\rm {heat}}\rangle ={\frac {D_{p}}{M}}$

and the final temperature will come from $k_{B}T={\frac {D_{p}}{\alpha }}$.

Momentum diffusion in the dressed atom picture

In the radiative cascade picture, as the atom cascades through the dressed levels, it experiences a force which is the same in magnitude, but reverses direction from left to right. Thus, we want to write down a statistical average over these fluctuating forces to get the momentum diffusion rate we want.

On resonance, the correlation time, the time range over which forces at time $\tau$ is related to the force at time $0$, is $2/\Gamma$. Thus, the integral we have for the momentum diffusion coefficient should only go over this time period. It means we have that the momentum diffusion rate due to dipole forces is

$D_{dipole}\approx {\frac {\hbar ^{2}(\nabla \Omega _{1})^{2}}{2\Gamma }}\,.$

This is the momentum diffusion rate due to the simulated light force, on resonance.

Away from resonance, the correlation time changes, and there are additional complications, but the basic physics stay the same (see JOSAB paper). The result for arbitrary detuning $\delta _{L}$ is

$D_{dipole}\approx {\frac {\hbar ^{2}(\nabla \Omega _{1})^{2}}{2\Gamma }}\left({\frac {\Omega _{1}^{2}}{\Omega _{1}^{2}+2\delta _{L}^{2}}}\right)^{3}\,.$

Atoms moving in a standing wave: Sisyphus cooling

The stimulated force is a force which we can fully understand with the two-level atom. It is conceptually simple, and we have analytical expressions for the forces and energy levels. Now let us see what happens when the velocity is not just infinitesimal, but is very large. Instead of just a time lag, the atom is now pictured as flying like a roller coaster. This picture will let us see a cooling mechanism known as sisyphus cooling, that is in practice important. In practice, the multi-level nature of real atoms leads to stronger cooling than expected for two levels, but we can see the necessary insight for this mechanism with sisyphus cooling of two-level atoms.

Let us take the atom velocity to satisfy

$kv\geq \Gamma \,,$

meaning that the atom moves through several optical wavelengths within its spontaneous emission lifetime.

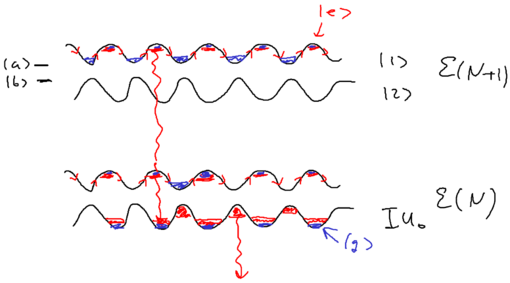
The nice thing about the dressed atom picture is that you can show wonderful drawings and diagrams, so let us draw a nice picture of a standing wave and show it for the manifold of dressed atom levels $1$ and $2$ within $E(N+1)$ What happens is that the standing wave modulates the energy of the atom in the two dressed states:

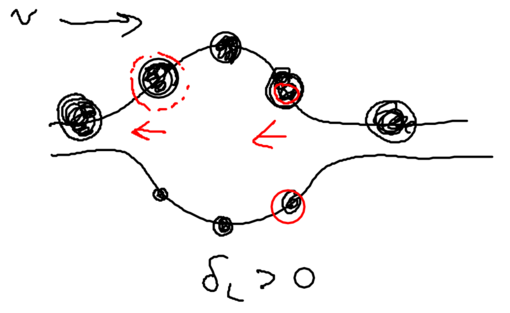
We assume that when we have no light, the ground state ($|a{\rangle }$, or $|g{\rangle }$) is the upper sate, and the excited state ($|b{\rangle }$, or $|e{\rangle }$) is the lower state. Suppose we start from the left, in this picture, and we go along the standing wave with the atom, which starts in its ground state. Where will the atom emit a photon, with highest probability, switching to the lower state through the radiative cascade? Will this happen at a node, or at an anti-node of the standing wave? The atom has the largest excited state admixture in the anti-nodes of the standing wave, so it is there where the atom emits.

So where the atom end up after emitting a photon? It can end in an upper state, at which point nothing changes with respect to forces on it, since it has stayed in the same dressed level. More interesting is what happens when the radiative cascade leads the atom to the lower dressed level:

When an atom ends up in the lower dressed level, when is it most likely to emit the next photon? The lower level is correlated with the excited state, so when there is no light, it atom is purely in its excited state. As it enters an anti-node, the atom evolves into a superposition of the excited and ground states. So it is most likely to emit when it is purely in the dark, meaning where the splitting of states is minimal.

This happens at the top of the hill. Thus, the physical picture is that the atom has to climb up a potential hill again whereupon it can once again emit a photon. In Greek mythology, King Sisyphus did something bad, so he had to roll a stone up a hill, and when it reached the top it fell down again, and he then had to roll it up the hill again. This is what happens with the atoms in this standing wave: it continuously climbs a hill.

The result we have is that for both dressed states $1$ and $2$, we have a preferential spontaneous emission at the top of the hill. This implies cooling, at the rate proportional to

$U_{0}\Gamma _{1\rightarrow 2}\Pi _{1}\,,$

where $U_{0}$ is the kinetic energy difference between the top and bottom of the standing wave potential hill. $\Gamma _{1\rightarrow 2}$ is the rate of the switching between sidebands of the radiative cascade.

Experimental implementation

See <refbase>5253</refbase>

This experiment did laser cooling of an atomic beam, and showed that with a blue detuned standing wave the beam velocity distribution narrowed (cooling the atoms), and with a red detuned standing wave it broadened (heating the atoms).

Dressed atoms in a perturbative limit: cooling in a standing wave

Let us now use the dressed atom picture to give, in the simplest limit (a perturbative limit), a summary of concepts of laser cooling in a standing wave. We take $\delta _{L}\gg \Omega _{1}\gg \Gamma$, neglect factors of the order of unity, and take $\hbar =1$.

If we have a standing wave,

$\Omega _{1}(x)=2\Omega _{1}\cos kx$

the two dressed levels are, to leading order,

${\begin{aligned}|1\rangle &=|a\rangle +{\frac {\Omega _{1}(x)}{\delta _{L}}}|b{\rangle }\\|2\rangle &=|b\rangle -{\frac {\Omega _{1}(x)}{\delta _{L}}}|a{\rangle }\,.\end{aligned}}$

These simple expressions give us the transition rate from $1$ to $2$,

$\Gamma _{1\rightarrow 2}=\Gamma \left({\frac {\Omega _{1}(x)}{\delta _{L}}}\right)^{4}\,,$

since the atom must start in the excited state and end up in the ground state. The transition rate from $2$ to $1$ is just

$\Gamma _{2\rightarrow 1}=\Gamma \,,$

in this perturbative limit.

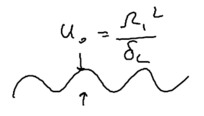
The energy of the dressed states change in the standing wave, giving us what we can call the "dressed state potential," which is physically nothing more than the AC stark shift

with potential height $U_{0}=\Omega _{1}^{2}/\delta _{L}$.

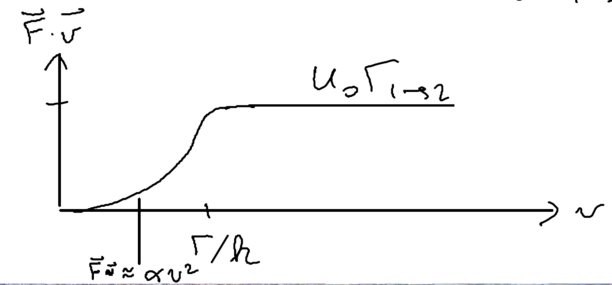
In this picture, we can go back to look at Sisyphus cooling once more, staring with the assumption $v\geq \Gamma /k$, but relaxing this to look at intermediate velocities. The cooling rate is ${\vec {F}}\cdot {\vec {v}}=U_{0}\Gamma _{1\rightarrow 2}$ (note that $\Gamma _{2\rightarrow 1}=\Gamma$ which happens much faster and thus is not limiting). When the velocity of that atom is much smaller, it cannot climb up and down many hills. But we know that the friction force is linear, so we expect what we have in intermediate velocity regimes is that there is some energy loss rate $\alpha v^{2}$:

Using the model that we have an initial parabola followed by a straight line, we obtain an estimate for the friction force

${\begin{aligned}\alpha &\approx \lim _{v\rightarrow 0}{\frac {F(v)}{v}}\approx {\frac {U_{0}\Gamma _{1\rightarrow 2}}{(\Gamma /k)^{2}}}\\&={\frac {\Omega _{1}^{2}}{\delta }}{\frac {\Gamma \Omega _{1}^{4}}{\delta _{L}^{4}}}{\frac {k^{2}}{\Gamma ^{2}}}\\&={\frac {\Omega _{1}^{6}}{\delta _{L}^{5}}}{\frac {k^{2}}{\Gamma }}\,.\end{aligned}}$

Thus, we find very nicely that the perturbative approach gives all the essential physics of what we derived above in a more rigorous manner.

Diffusion

It turns out that the limit of cooling is always higher than the depth of the optical lattice, and to understand this we need to return to the diffusion coefficient. Building on our perturbative expressions, recalling that

$D=\int \langle \Delta F(0)\Delta F(t)\rangle dt\,,$

we may use the fact that the atoms are mainly in state $|1{\rangle }$. The interesting situation is when the atoms are on the slope of the standing wave, where $F_{1}=-\nabla U_{1}(v)\approx kU_{0}$. For a duration $1/\Gamma$, at rate $\Gamma _{1\rightarrow 2}$, the atom jumps and the force also jumps, to the opposite value $-\nabla U_{2}=-kU_{0}$.

Graphically, we may see what happens by plotting the force seen by a typical atom as a function of time:

In the initial dressed level, the atom sees a constant force, then emits a photon, going to the other dressed level (essentially the excited state) for a short time $1/\Gamma$, before returning. The dominant contribution to the force comes from these brief spikes, so the momentum diffusion coefficient can be written down by inspection as

$D=(kU_{0})^{2}/\Gamma {\frac {\frac {1}{\Gamma }}{\frac {1}{\Gamma _{1\rightarrow 2}}}}$

where the expression on the right is the probability that the atom is in state $|2{\rangle }$, in our picture.

Plugging in numbers, we get

$D=k^{2}U_{0}^{2}\Gamma _{1\rightarrow 2}/\Gamma ^{2}$

The ultimate temperature limit achievable from this cooling is thus

$k_{B}T={\frac {D}{\alpha }}=U_{0}\,.$

This means that, according to the perturbative approach, there is competition between cooling and heating, resulting in a minimum temperature set by the depth of the lattice. Keep in mind that cooling to zero temperature cannot be accomplished either, using this mechanism, since the analysis assumes that $U_{0}>\Gamma$. Two-level atoms therefore cannot be localized in an optical lattice by stimulated laser cooling. The only reason why localization of atoms in a lattice is possible is through other mechanisms, such as polarization gradient cooling.

References

• Important paper: J. Dalibard and C. Cohen-Tannoudji, J. Opt. Soc. Am .B 2, 1707 (1985) Download