The operator sum representation of open quantum system dynamics

The operator sum representation of open quantum system dynamics

Modern atomic physics rests on engineering the physics of quantum systems, and one of the greatest parts of this challenge is control of decoherence. Beginning with the ideas born from manipulating spontaneous emission rates with optical cavities, the study of open quantum system dynamics has grown to encompass laser physics, cooling of atoms, and nascent thoughts on quantum thermodynamics. And one of the most important of the new reaches of this study is the development of quantum error correction, by which open quantum system dynamics can be reversed, under certain circumstances.

The master equation and quantum trajectories approaches to this study have in common their use of continuous time in describing open quantum system dynamics. However, it is often not important to be able to know the state of a system at all times. In fact, in increasingly many experiments, what is needed is knowledge of the state only at discrete times, such as before and after some operation. For example, in quantum information science, such operations can be individual logic gates, or full communication protocols such as teleportation or entanglement distillation.

Very generally, a discrete time picture is exceedingly useful in modeling and analyzing noisy channels, such as are used in communication. In the world of classical physics, Shannon's theory of how to communicate reliably over noisy channels led to the development of modern information theory, and error correction codes. Analogously, quantum information theory has developed to describe how to communicate reliably over noisy quantum channels, with a slew of novel quantum error correction codes. Among other things, such codes allow reliable information processing systems to be realized from unreliable components, provided the component failure probabilities are beneath a fixed threshold set by code properties.

In this section, we present a discrete time model of open quantum system dynamics, known as the operator sum representation ("OSR"). One nice feature of this representation is that the Lindblad form of the master equation can be derived from it, as we show. The OSR also provides a comprehensive way to grasp the different unravelings possible for open system dynamics, as we describe with examples demonstrating quantum error correction.

OSR: definition and properties

Suppose the system under study is described by state $|\psi {\rangle }$. It interacts with an environment, initially in some state $|e{\rangle }$, through a unitary interaction $U$, producing

$|e{\rangle }|\psi \rangle \longrightarrow U|e{\rangle }|\psi {\rangle }\,.$

Suppose the output state of the environment is measured in the basis $\{|e_{k}{\rangle }\}$ (all mutually orthogonal). Since the environment is doing the measuring, the measurement results are left unknown, but this does not change the fact that the resulting state of the system is given by averaging over the environment's measurement results. Using the notation

$\rho =\sum _{k}p_{k}|\phi _{k}{\rangle }{\langle }\phi _{k}|\longleftrightarrow \rho ={\sqrt {p_{0}}}|\phi _{0}\rangle \oplus {\sqrt {p_{1}}}|\phi _{1}\rangle \oplus \cdots \,,$

we can write the resulting system as the statistical mixture of states

$\langle e_{0}|U|e{\rangle }\,|\psi {\rangle }\oplus \langle e_{1}|U|e{\rangle }\,|\psi {\rangle }\oplus \langle e_{2}|U|e{\rangle }\,|\psi \rangle \cdots \,.$

Let $E_{k}=\langle e_{k}|U|e{\rangle }$ be the operator (in the Hilbert space of the system) given by the partial matrix element over the environment with $|e{\rangle }$ and $|e_{k}{\rangle }$. The output state of the system is thus

$\rho _{out}={\mathcal {E}}(\rho _{in})=\sum _{k}E_{k}\rho _{in}E_{k}^{\dagger }\,,$

(6.3.1)

where $\rho _{in}=|\psi {\rangle }{\langle }\psi |$ is the input system state. Note that by construction,

$\sum _{k}E_{k}^{\dagger }E_{k}=\sum _{k}\langle e|U^{\dagger }|e_{k}{\rangle }\langle e_{k}|U|e\rangle =I\,,$

where $I$ is the identity operator acting in the Hilbert space of the system.

Eq.(6.3.1) is known as the operator sum representation, and the $E_{k}$ are known as operation elements, or {\em Kraus operators}. When the operation elements satisfy $\sum _{k}E_{k}^{\dagger }E_{k}=I$, a constraint known as the completeness relation, the corresponding ${\mathcal {E}}(\cdot )$ satisfies three important properties, that

• ${\rm {Tr}}[{\mathcal {E}}(\rho )]=1$ for all $\rho$ with ${\rm {Tr}}(\rho )=1$.
• ${\mathcal {E}}$ is manifestly convex and linear, that is

${\mathcal {E}}\left(\sum _{k}p_{k}\rho _{k}\right)=\sum _{k}p_{k}{\mathcal {E}}(\rho _{k})\,.$

• ${\mathcal {E}}$ is completely positive, meaning that if $\rho \geq 0$ then ${\mathcal {E}}(\rho )\geq 0$ (it is a positive operator), and $(I_{R}\otimes {\mathcal {E}}_{Q})(\rho _{RQ})\geq 0$ for any $\rho _{RQ}\geq 0$ (acting on just a part of system still produces a legitimate state).

Proving that ${\mathcal {E}}$ leaves the trace unchanged is easy, but providing complete positivity is outside of the scope of this brief introduction (see, for example, Chapter 8 of Nielsen and Chuang, for a proof). Moreover, it turns out that if a quantum operation is {\em defined} as being a map satisfying these three properties, then it must have an operator sum representation, so the OSR is indeed very fundamental.

The practical importance of the operator sum representation lies in the fact that any set of operators satisfying $\sum _{k}E_{k}^{\dagger }E_{k}=I$ defines a valid OSR, and that all interactions with an environment can be described by some set of operation elements satisfying $\sum _{k}E_{k}^{\dagger }E_{k}=I$. It is also useful to know that for a system of $N$ dimensions, the maximum number of operation elements needed to describe an arbitrary interaction with an environment is $N^{2}$.

OSR: examples

Let us consider some examples of some simple operator sum representations of interactions.

1. When there is no interaction with an environment, the operation element is a unitary transform $U$, such that ${\mathcal {E}}(\rho )=U\rho U^{\dagger }$.

2. When the interaction is measurement with projectors $\{P_{k}\}$, then ${\mathcal {E}}(\rho )=\sum _{k}P_{k}\rho P_{k}$.

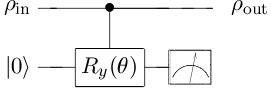
3. Suppose the interaction is

where the box with line represents a controlled rotation about the ${\hat {y}}$ axis by angle $\theta$, and the "environment" is modeled as a single qubit. The resulting operation elements are

${\begin{aligned}E_{0}&=\left[{\begin{array}{cc}{1}&{0}\\{0}&{\sqrt {1-\lambda }}\end{array}}\right]\\E_{1}&=\left[{\begin{array}{cc}{0}&{0}\\{0}&{\sqrt {\lambda }}\end{array}}\right]\,,\end{aligned}}$

where ${\sqrt {\lambda }}=\sin \theta /2$. Direct calculations shows that

${\mathcal {E}}\left(\left[{\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}}\right]\right)=\sum _{k}E_{k}\left[{\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}}\right]E_{k}^{\dagger }=\left[{\begin{array}{cc}{a}&{b{\sqrt {\lambda }}}\\{c{\sqrt {\lambda }}}&{d}\end{array}}\right]\,,$

which is the transformation expected for pure phase damping ($T_{2}$).

4. For amplitude damping of a single qubit, the operation elements are similar to those for phase damping:

${\begin{aligned}E_{0}&=\left[{\begin{array}{cc}{1}&{0}\\{0}&{\sqrt {1-\lambda }}\end{array}}\right]\\E_{1}&=\left[{\begin{array}{cc}{0}&{\sqrt {\lambda }}\\{0}&{0}\end{array}}\right]\,.\end{aligned}}$

Unitary degree of freedom in the operator sum representation

Multiple choices of operation elements lead to the same density matrix mapping $\rho \rightarrow {\mathcal {E}}(\rho )$. This is a consequence of the infinite number of unravelings of density matrices into pure state ensembles, manifested in this representation by the fact that the map cannot depend on the environment's choice of measurement basis:

In this diagram, the unitary transform $U'$ inserted before the environment's measurement parameterizes this unitary degree of freedom in the OSR. It leads to the fact that if $\{E_{k}\}$ are a valid set of operation elements for ${\mathcal {E}}$, then

$F_{j}=\sum _{k}U_{jk}E_{k}$

also give a valid set of operation elements, for any unitary matrix with elements $U_{jk}$.

An example of this is the fact that

${\begin{aligned}F_{0}&={\sqrt {\alpha }}\left[{\begin{array}{cc}{1}&{0}\\{0}&{1}\end{array}}\right]\\F_{1}&={\sqrt {1-\alpha }}\left[{\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}}\right]\end{aligned}}$

defines an OSR equivalent to that given earlier, for phase damping, for appropriate choice of $\alpha$.

From OSR to master equation in Lindblad form

We have previously seen that open quantum systems can be described by a master equation in Lindblad form, namely

${\dot {\rho }}=-i[H,\rho ]+\sum _{k}\left[{L_{k}\rho L_{k}^{\dagger }-{\frac {1}{2}}(L_{k}^{\dagger }L_{k}\rho +\rho L_{k}^{\dagger }L_{k})}\right]\,,$

where $L_{k}$ are jump operators. It has been stated that this form is necessary to guarantee physical validity (trace preservation and complete positivity), but no derivation origin has been given.

A master equation in Lindblad form can be derived from an operator sum representation ${\mathcal {E}}$ for an interaction with an environment, in the following way. Let $\tau$, parameterize the strength of the interaction, such that we may approximate

${\frac {d\rho }{dt}}\approx {\frac {{\mathcal {E}}(\rho )-\rho }{\tau }}\,,$

in the same spirit of coarse-grained evolution in which master equations are derived. Without loss of generality, one of the operation elements for ${\mathcal {E}}$ should be of the order of unity, such that to leading order,

$E_{0}=I-iK\tau +O(\tau ^{2})\,,$

where $K$ is independent of $\tau$.

Define $H=(K+K^{\dagger })/2$ and $J=i(K-K^{\dagger })/2$ as being the hermitean and anti-hermitean parts of $K$, such that $H$ describes the first-order Hamiltonian evolution under ${\mathcal {E}}$. Specifically, to leading order in $\tau$,

$E_{0}\rho E_{0}^{\dagger }=\rho -i\tau [H,\rho ]-\tau (J\rho +\rho J)\,.$

Because of the completeness relation $\sum _{k}E_{k}^{\dagger }E_{k}=I$,

$\sum _{k\neq 0}E_{k}^{\dagger }E_{k}=I-E_{0}^{\dagger }E_{0}\approx I-(I+iK^{\dagger }\tau )(I-iK\tau )\approx 2J\tau$

The terms in the OSR with $k\neq 0$ are of order $\tau$, so that we may define

$L_{k}={\frac {E_{k}}{\sqrt {\tau }}}\,.$

Thus, to leading order in $\tau$, we may express $J$ in terms of $L_{k}$ as

$J={\frac {1}{2}}\sum _{k\neq 0}L_{k}^{\dagger }L_{k}\,,$

giving

${\mathcal {E}}(\rho )=\sum _{k}E_{k}\rho E_{k}^{\dagger }\approx \rho -i\tau [H,\rho ]+\tau \sum _{k\neq 0}\left[{L_{k}\rho L_{k}^{\dagger }-{\frac {1}{2}}L_{k}^{\dagger }L_{k}\rho -{\frac {1}{2}}\rho L_{k}^{\dagger }L_{k}}\right]\,.$

Finally, this produces the coarse-grained equation of motion

${\dot {\rho }}=-i[H,\rho ]+\sum _{k\neq 0}L_{k}\rho L_{k}^{\dagger }-{\frac {1}{2}}L_{k}^{\dagger }L_{k}\rho -{\frac {1}{2}}\rho L_{k}^{\dagger }L_{k}\,,$

which is the desired master equation in Lindblad form.

The key steps to keep in mind, in this identification between the operator sum representation ${\mathcal {E}}$ and the master equation, are

• The Hamiltonian changes from the original system Hamiltonian $H_{0}$ to becoming $H_{0}+H$, where $H$ is derived from the unity-order operation element in ${\mathcal {E}}$. Often, $H$ may be small, causing a small renormalization of energies, such as in the Lamb shift associated with spontaneous emission decay. However, it can also be substantial and not commute with $H_{0}$, as demonstrated by other unravelings of spontaneous emission.
• The remaining operation elements in ${\mathcal {E}}$ define the jump operators, when expanded to leading order in ${\sqrt {\tau }}$, for small interaction parameter $\tau$.

Quantum error correction

Perhaps one of the most surprising and fundamentally interesting results from quantum information is quantum error correction. Classical error correction is a process used to reverse random errors which happen, say in a communication channel, which undesirably distorts a message being transmitted. This can be accomplished, for example, using redundancy, say by repeating the transmission of a given message three or more times, and using majority voting to recover the original at the receiver.

However, before 1995, it was believed that such an error correction concept could not apply to quantum systems, because

• Quantum states collapse when measured
• Errors are continuous
• Quantum states cannot be cloned

In particular, for example, one cannot encode a quantum state $|\psi {\rangle }$ against errors simply by replicating it three or more times, as $|\psi {\rangle }|\psi {\rangle }|\psi {\rangle }\cdots$. Such perfect "cloning" is known to be fundamentally impossible within the framework of quantum mechanics, and furthermore, even with such a state in hand, errors to $|\psi {\rangle }$ cannot in general be corrected simply by using redundant copies.

Nevertheless, it turns out there are ways around all of these objections. The part of the Hilbert space containing the information about the state you wish to preserve need not be measured; only the effect of the environment need be determined by a measurement. And using entangled states allow errors to be made orthogonal and distinguishable; entanglement also replaces the role played by redundant copies in classical error correction.

Here, we illustrate the basic ideas behind quantum error correction using a set of specific examples.

3-qubit bit-flip code

Suppose errors occur to a qubit as described by the quantum operation ${\mathcal {E}}(\rho )=(1-p)\rho +pX\rho X$, where $p$ is a probability. This process is known as a "bit-flip" channel, because the qubit is left alone with probability $1-p$, and flipped by $X$ with probability $p$. We provide in the following an encoding and recovery method, allowing bit-flip errors on an unknown qubit to be corrected.

The first key idea is to encode using entangled states, rather than using redundancy. Define "logical zero" as $|0_{L}\rangle =|000{\rangle }$ and "logical one" as $|1_{L}\rangle =|111{\rangle }$, and suppose instead of sending $a|0{\rangle }+b|1{\rangle }$ through the channel, instead we send $a|0_{L}{\rangle }+b|1_{L}{\rangle }$. Much like for a classical three-bit majority voting code, we find that the effect of the quantum noise process (acting independently and identically on the three qubits in the code) performs the transformation

$a|0_{L}\rangle +b|1_{L}\rangle {\stackrel {\mathcal {E}}{\rightarrow }}\left\{{\begin{array}{lc}a|000{\rangle }+b|111{\rangle }~~~~&(1-p)^{3}\\a|001{\rangle }+b|110{\rangle }~~~~&p(1-p)^{2}\\a|010{\rangle }+b|101{\rangle }~~~~&p(1-p)^{2}\\a|100{\rangle }+b|011{\rangle }~~~~&p(1-p)^{2}\\a|011{\rangle }+b|100{\rangle }~~~~&p^{2}(1-p)\\a|101{\rangle }+b|010{\rangle }~~~~&p^{2}(1-p)\\a|110{\rangle }+b|001{\rangle }~~~~&p^{2}(1-p)\\a|111{\rangle }+b|000{\rangle }~~~~&p^{3}\end{array}}\right.\,,$

where the probabilities of each pathway are given in the column on the right. The output state of the channel is the resulting statistical mixture of states.

Classical error correction would proceed by measuring the noisy output, processing the measurement, then reconstructing the original with high fidelity. Quantum error correction, however, must be more subtle. Here is the second key idea: instead of projectively measuring the output state, we perform partial measurements, to determine only the effect of the environment, and leave the encoded qubit untouched, with high probability.

Specifically, suppose that pairs of qubits can be measured, to determine if they are identical (either $00$ or $11$, or opposite, $01$ or $10$), without revealing the specific values of the qubits. Define two such parity measurements,

$U_{1}=Z_{1}Z_{2}=ZZI~~~~~~{\rm {and}}~~~~~~U_{2}=Z_{2}Z_{3}=IZZ\,,$

corresponding to measuring the parities of the first and second qubits, and the second and third qubits, respectively. Let the output of these measurements be $0$ if the two qubits are identical, and $1$ otherwise.

Considering just the four high probability output states, we find the following:

${\begin{array}{cccc}{\rm {State}}&U_{1}~{\rm {result}}&U_{2}~{\rm {result}}&{\rm {Recovery~operation}}\\a|000\rangle +b|111\rangle &0&0&I\\a|001\rangle +b|110\rangle &0&1&X_{3}\\a|010\rangle +b|101\rangle &1&1&X_{2}\\a|100\rangle +b|011\rangle &1&0&X_{1}\end{array}}\,,$

where the second and third columns give the measurement results for $U_{1}$ and $U_{2}$, known as the syndrome. Note that none of the measurement results distinguish between $a$ and $b$, and thus the encoded qubit is left intact. After doing this measurement, we can recover the initial state $a|0_{L}{\rangle }+b|1_{L}{\rangle }$ by applying the unitary transformation given in the fourth column.

The final output state $\rho$ after performing this correction procedure is not perfect, because of the probability of two or more errors occurring. Quantitatively, the fidelity of the reconstructed state is

$F(\rho ,|\psi \rangle )={\sqrt {{\langle }\psi |\rho |\psi {\rangle }}}={\sqrt {1-3p^{2}+2p^{3}}}\,.$

Interestingly, this scheme also corrects a small rotational error, even though the error is continuous! Let the error be described by the quantum operation

${\mathcal {E}}(\rho )=e^{-i\epsilon X_{1}}\rho e^{i\epsilon X_{1}}\,.$

We have that $|\psi '\rangle =R_{x_{1}}(2\epsilon )|\psi \rangle =|\psi \rangle -i\epsilon X_{1}|\psi {\rangle }$, so the syndrome measurement result collapses this state into either $|\psi {\rangle }$ or $-i\epsilon X_{1}|\psi {\rangle }$. The fidelity of the resulting output, after recovery ${\mathcal {R}}$, is

$F({\mathcal {R}}({\mathcal {E}}(|\psi \rangle )),|\psi \rangle )\approx {\sqrt {1-\epsilon ^{4}}}\approx 1-\epsilon ^{2}\,.$

In comparison, if no encoding were done then the output fidelity would have been $\approx 1-\epsilon$. This reduction of error from $O(\epsilon )$ to $O(\epsilon ^{2})$ is a signature of the success of the error correction, even for continuous errors.

3-qubit phase-flip code

A similar procedure can be used to correct phase flip errors. Let ${\mathcal {E}}(\rho )=(1-p)\rho +pZ\rho Z$. Recall that $HZH=X$ and $HXH=Z$. Thus, $H{\mathcal {E}}(H\rho H)H={\mathcal {E}}_{\rm {bit~flip}}$. Thus, we can correct phase flip errors by the encoding $|0_{L}\rangle =|{\rm {+++}}{\rangle }$, $|1_{L}\rangle =|{\rm {{-}{-}{-}}}{\rangle }$, where $|{\pm }{\rangle }\equiv (|0{\rangle }\pm |1\rangle )/{\sqrt {2}}$, and we perform the syndrome measurements $XXI$ and $IXX$.

Arbitrary errors are superpositions of bit-flip and phase-flip errors

The reason phase flip errors are significant and interesting is because of the following.

bit-flip ($X$), phase-flip ($Z$), and bit-phase flip ($XZ$) errors.

can be written as ${\mathcal {E}}(\rho )=\sum _{k}E_{k}\rho E_{k}^{\dagger }$. Let $\rho$ be a single qubit, and define $E_{k}=\sum _{j}c_{jk}\sigma _{j}$, where $\sigma _{j}\in \{I,X,Y,Z\}$. Then

${\begin{array}{rcl}{\mathcal {E}}(\rho )&=&\sum _{kjj'}c_{kj}x_{kj'}^{*}\sigma _{j}\rho \sigma _{j'}\\&=&\sum _{kl}\chi _{jl}\sigma _{j}\rho \sigma _{l}\,,\end{array}}$

where $\chi _{jl}=\sum _{k}c_{kj}c^{*}{kj'}$ is a matrix of c-number coefficients.

For example, for $R_{x}(2\epsilon )|\psi \rangle \approx |\psi \rangle -i\epsilon X|\psi {\rangle }$, we have ${\mathcal {E}}(\rho )=\rho -i\epsilon (X\rho -\rho X)+\epsilon ^{2}X\rho X$. The syndrome measurement then projects the environment into definite error states, removing the off-diagonal terms (proportional to $\epsilon$ instead of to $\epsilon ^{2}$) in this expression.

Quantum error correction: Shor's 9-qubit code

A combination of the bit-flip and phase-flip codes allows correction of any single qubit error. This code encodes a single qubit as

${\begin{aligned}|0_{L}\rangle &={\frac {(|000\rangle +|111\rangle )^{\otimes 3}}{\sqrt {8}}}\\|1_{L}\rangle &={\frac {(|000\rangle -|111\rangle )^{\otimes 3}}{\sqrt {8}}}\,.\end{aligned}}$

The syndrome measurement operators are

$Z_{1}Z_{2},~~Z_{2},Z_{3},~~Z_{4},Z_{5},~~Z_{5},Z_{6},~~Z_{7},Z_{8},~~{\rm {and}}~~Z_{8},Z_{9}$

for bit flip errors, and

$X_{1}X_{2}X_{3}X_{4}X_{5}X_{6}~~~~~~X_{4}X_{5}X_{6}X_{7}X_{8}X_{9}$

for phase flip errors. It is simple to see that any single qubit bit flip or phase flip or bit-phase flip error gives a unique syndrome measurement result, by direct examination. It corrects to leading order errors resulting from small rotations, as well. And perhaps, not so obviously, the code also perfectly corrects for errors resulting from removal of any single qubit!