Atoms in electric fields
This section deals with how atoms behave in static electric fields. The method is straightforward, involving second order perturbation theory. The treatment describes the effects of symmetry on the basic interaction, polarizability, and the concept of oscillator strength.
Contents
- 1 Review: Parity
- 2 Review: Results of Stationary Perturbation Theory
- 3 Supplement: The Hydrogen Atom in a Static Electric Field
- 4 Perturbation Theory of Polarizability
- 5 Beyond the quadratic Stark effect
- 6 Field ionization
- 7 Atoms in an Oscillating Electric Field
- 8 Oscillator Strength
- 9 Index of refraction
- 10 References
Review: Parity
Review: Results of Stationary Perturbation Theory
Supplement: The Hydrogen Atom in a Static Electric Field
Perturbation Theory of Polarizability
We will find the energy and polarizability of an atom in a static field along the +z direction. We apply perturbation theory taking to describe the unperturbed atomic system and
Non-degenerate eigenstates have to be eigenstates of parity. Since is odd under parity operation, parity requires that . So the first order perturbation vanishes. To second order, the energy is given by
If we define now the polarizability in state as
- {EQ_polarsix}
we obtain
The dipole moment is the expectation value of the dipole operator, using the first order perturbed state vector.
where the sum is over Only the term will contribute, and we can express the induced dipole moment by the polarizability:
Note that the Stark shift is and not equal to . is the expectation value for the electrostatic potential energy of the dipole moment, but the total energy change is only one half of this since energy is needed to admix excited states into the ground state.
Note that polarizability has the dimensions of length, i.e. volume. As an example, for the ground state of hydrogen we can obtain a lower limit for the polarizability by considering only the contribution to the sum of the state. Values for the various moments in hydrogen are given in Bethe and Salpeter, Section 63. Using = 1.666, and , we obtain atomic units (i.e. ).
The polarizability of the ground state of hydrogen can be calculated exactly. It turns out that the state makes the major contribution, and that the higher bound states contribute relatively little. However, the continuum makes a significant contributions. The exact value is 4.5.
To put the above result for the polarizability in perspective, note that the potential of a conducting sphere of radius in a uniform electric field is given by
The induced dipole moment is , so that the polarizability is . For the ground state of hydrogen, , so to a crude approximation, in an electric field hydrogen behaves like a conducting sphere.
Polarizability may be approximated easily, though not accurately, using Unsold's approximation in which the energy term in the denominator of Eq. \ref{EQ_polarsix} is replaced by an average energy interval . The sum can then be evaluated using the closure rule . (Note that the term does not need to be excluded from the sum, since .). With this approximation,
For hydrogen in the ground state, . If we take the average excitation energy to be , the result is .
Beyond the quadratic Stark effect
It should be obvious from the previous discussion that the Stark effect for a state of is quadratic only when
(EQ_ beyondone)
when is the nearest state of opposite parity to .
If is the ground state, we can expect Hartree and (virial theorem). Hence the Stark shift should be quadratic if the field is well below the critical value
(EQ_ beyondtwo)
[ is atomic unit of field] —a field three orders of magnitude in excess of what can be produced in a laboratory except in a vanishingly small volume.
If is an excited state, say , this situation changes <it> dramatically </it>. In general, the matrix element and to the next level of opposite parity depends on the quantum defect:
(EQ_ beyondthree)
Thus the critical field is lowered to
(EQ_ beyondfour)
Considering that quantum defects are typically when is the largest of an electron in the core), it is clear that even 1 V/cm fields will exceed for higher levels if . Large laboratory fields ( V/cm) can exceed even for states if .
When the electric field exceeds states with different but the same are degenerate to the extent that their quantum defects are small. Once exceeds the number of core electrons, these states will easily become completely mixed by the field and they must be diagonalized exactly. The result is eigenstates possessing apparently permanent electric dipoles with a resulting linear Stark shift (see following figure). As the field increases, these states spread out in energy. First they run into states with the same but different quantum defects; then the groups of states with different begin to overlap. At this point a matrix containing all states with greater or equal to must be diagonalized. The only saving grace is that the lowest states do not partake in this strong mixing; however, the states near the continuum always do if there is an -field present.\
The situation described above differs qualitatively for hydrogen since it has no quantum defects and the energies are degenerate. In this case the zero-field problem may be solved using a basis which diagonalizes the Hamiltonian both for the atom above and also in the presence of an electric field. This approach corresponds to solving the H atom in parabolic–ellipsoidal coordinates and results in the presence of an integral quantum number which replaces . The resulting states possess permanent dipole moments which vary with this quantum number and therefore have linear Stark effects even in infinitesimal fields. Moreover the matrix elements which mix states from different manifolds vanish at all fields, so the upper energy levels from one manifold cross the lower energy levels from the manifold above without interacting with them.\
The following example shows the high field stark effect for Li. Only the term in Li has an appreciable quantum defect, and it has been suppressed by selecting final states with .
The dramatic difference between the physical properties of atoms with and the properties of the same atoms in their ground state, coupled with the fact that these properties are largely independent of the type of atom which is excited, justifies the application of the name Rydberg atoms to highly excited atoms in general.\
Field ionization
If an atom is placed in a sufficiently high electric field it will be ionized, a process called <it> field ionization </it>. An excellent order of magnitude estimate of the field , required to ionize an atom which is initially in a level bound by energy can be obtained by the following purely classical argument: the presence of the field adds the term to the potential energy of the atom. This produces a potential with a maximum and the atom will ionize if .
The figure shows the combined potential as well as and
(EQ_ fieldionone)
The appropriate maximum occurs at
(EQ_ fieldiontwo)
as determined from . Equating and gives
(EQ_ fieldionthree)
for level with energy and quantum number .
The predictions of this formula for is usually accurate within 20% in spite of its neglect of both quantum tunneling and the change in produced by the field. [This latter deficiency is remedied in the comparison with Li data shown in the preceding part of this section because the eye naturally uses the ionization field appropriate to the perturbed energy of the state rather than its zero-field energy.] Tunneling manifests itself as a finite decay rate for states which classically lie lower than the barrier. The increase of the ionization rate with field is so dramatic, however, that the details of the experiment do not influence the field at which ionization occurs very much: calculations [u'BHR65'] show the ionization rate increasing from /sec to /sec for a 30% increase in the field.\
Oddly enough the classical prediction works worse for H than for any other atom. This is a reflection of the fact that certain matrix elements necessary to mix the states (so the wave function samples the region near ) are rigorously zero in H, as discussed in the preceding part of this section. Hence the orbital ellipse of the electron does not precess and can remain on the side of the nucleus. There its energy will increase with , but it will not spill over the lip of the potential and ionize.
Atoms in an Oscillating Electric Field
There is a close connection between the behavior of an atom in a static electric field and its response to an oscillating field, i.e. a connection between the Stark effect and radiation processes. In the former case, the field induces a static dipole moment; in the latter case, it induces an oscillating moment. An oscillating moment creates an oscillating macroscopic polarization and leads to the absorption and emission of radiation. We shall calculate the response of an atom to an oscillating field
where is the polarization vector for the field. For a weak field the time varying state of this system can be found from first order time dependent perturbation theory. We shall write the electric dipole operator as D = -er. (This is a change of notation. Previously the symbol was d.) The Hamiltonian naturally separates into two parts, , where is the unperturbed Hamiltonian and
We shall express the solution of the time dependent Schroedinger equation in terms of the eigenstates of .
where . Because of the perturbation , the 's become time dependent, and we have
Left multiplying the final two expressions by to project out the -th terms yields
where . In perturbation theory, this set of equations is solved by a set of approximations to labeled . Starting with
one sets
and solves for the successive approximations by integration.
We now apply this to the problem of an atom which is in its ground state at , and which is subject to the interaction of Eq.\ \ref{EQ_atomoef2}. Consequently , . Substituting in Eq.\ \ref{EQ_atomoef7} and integrating from to gives
The -1 terms in the square bracketed term arises because it is assumed that the field was turned on instantaneously at . They represent transients that rapidly damp and can be neglected.
The term with , in the denominator is the counter-rotating term. It can be neglected if one is considering cases where (i.e. near resonance), but we shall retain both terms and calculate the expectation value of the first order time dependent dipole operator
If we consider the case of linearly polarized light , then
We can write in terms of a polarizability :
This result diverges if . Later, when we introduce radiative damping, the divergence will be avoided in the usual way.
Oscillator Strength
Eq.\ \ref{EQ_atomoef11} resemble the oscillating dipole moment of a system of classical oscillators. Consider a set of oscillators having charge , mass Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} , and natural frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_k} , driven by the field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E} \cos \omega t} . The amplitude of the motion is given by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_k = \frac{q_k}{m(\omega_k^2 - \omega^2)} \mathcal{E} \cos \omega t }
If we have a set of such oscillators, then the total oscillating moment is given by
This is strongly reminiscent of Eq.\ \ref{EQ_atomoef10}. It is useful to introduce the concept of oscillator strength, a dimensionless quantity defined as
where and are any two eigenstates. Note that is positive if , i.e. for absoprtion, and negative if Then, Eq.\ \ref{EQ_atomoef10} becomes
Comparing this with Eq.\ \ref{EQ_ostre2}, we see that the behavior of an atom in an oscillating field mimics a set of classical oscillators with the same frequencies as the eigenfrequencies of the atom, but having effective charge strengths Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_k^2 = f_{kg} e^2} .\\
The oscillator strength is useful for characterizing radiative interactions and also the susceptibiltiy of atoms. It satisfies an important sum rule, the Thomas-Reiche-Kuhn sum rule:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k} f_{kg} = 1 }
We prove by considering the general Hamiltonian
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H= \frac{1}{2} \sum_{j} p_j^2 + V(r_1 , r_2 \cdots ) . }
Using the commutator relation
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A,B^2] = [A,B] B+ B [A,B], }
and the relation , we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [r,H] = \frac{i\hbar}{m} p }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = \sum r_j} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = \sum p_j} . However,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle j | [r, H] |k \rangle = (E_k - E_n ) \langle j | r | k \rangle }
Consequently,
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{kj} = (E_k - E_j )/\hbar} . Thus, we can write Eq.\ \ref{EQ_ostre3} in either of two forms:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{kj} = \frac{2i}{\hbar} \langle j | p_z |k \rangle \langle |k|z|j \rangle = - \frac{2i}{\hbar} \langle k | p_z |j \rangle \langle |j|z|k \rangle }
Taking half the sum of these equations and using the closure relation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k} |k \rangle \langle k|=1} , we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k} f_{kj} = \frac{i}{\hbar} {\left[ \langle j |p_z z - z p_z | j \rangle \right]} = 1 }
We have calculated this for a one-electron atom, but the application to a Z-electron atom is straightforward because the Hamiltonian in Eq.\ \ref{EQ_ostre6} is quite general. In this case
Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} is some eigenstate of the system, and the index Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} describes all the eigenstates of all the electrons -- including continuum states. In cases where only a single electron will be excited, however, for instance in the optical regime of a "single-electron" atom where the inner core electrons are essentially unaffected by the radiation, the atom behaves as if it were a single electron system with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=1} .
Note that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{kj}} is positive if , i.e. if the final state lies above the initial state. Such a transition corresponds to absorption of a photon. Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{jk} = -f_{jk}} , the oscillator strength for emission of a photon is negative.
Our definition of oscillator strength, Eq.\ \ref{EQ_ostre3}, singles out a particular axis, the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{z}} -axis, fixed by the polarization of the light. Consequently, it depends on the orientation of the atom in the initial state and final states. It is convenient to introduce the average oscillator strength (often simply called the oscillator strength), by letting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z_{kj}|^2 \rightarrow |r_{kj } |^2/3} , summing over the initial Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} state and averaging over the final state.\\
(This is the conversion followed by Sobelman.) It is evident that
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{f_{jk}} = - \frac{2J_j + 1}{2J_k + 1}\overline{f_{kj}} = - \frac{g_j}{g_k} \overline{f_{kj}} , }
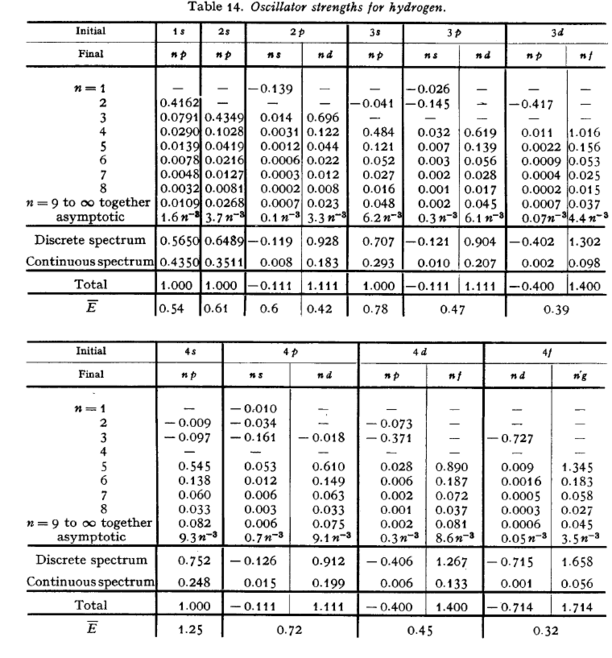
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_j} is the multiplicity factor for state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} . An extensive discussion of the sum rules and their applications to oscillator strengths and transition momentums can be found in Bethe and Salpeter, section 6.1. Among the interesting features they point out is that transitions from an initial state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n, \ell \rangle } to a final state on the average have stronger oscillator strengths for absorption if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell^\prime > \ell} , and stronger oscillator strengths for emission if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell^\prime < \ell} . In other words, atoms "like" to increase their angular momentum on absorption of a photon, and decrease it on emission. The following page gives a table of oscillator strengths for hydrogen in which this tendency can be readily identified. (Taken from {\it The Quantum Mechanics of One- and Two-Electron Atoms}, H.A. Bethe and E.E. Salpeter, Academic Press (1957).)
\caption{ Oscillator strengths for hydrogen. From Mechanics of One- and Two-Electron Atoms}
Index of refraction
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_r = sqrt{1 + 4 \pi n_{at} \alpha} \approx 1 + 2 \pi n_{at} \alpha }
In the case of a single strong resonance, we negletct the counter-rotating term, and let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta = \omega - \omega_{kg} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = -\frac{e^2}{\hbar} |\langle k|z|g\rangle|^2 \frac{1}{\delta} }
Define the natural linewidth
So we can rewrite the expression for the refractive index:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_r \approx 1 - 2 \pi n_{at} \frac{3 \Gamma}{4}\frac{c^3}{w^3}\frac{1}{\delta} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 1 - n_{at} \sigma_0 \frac{\lambda}{4\pi}\frac{\Gamma}{2\delta} }
where, since
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{c^3}{\omega^3}=\frac{lambda^3}{(2\pi)^3} }
we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_0 \equiv 6\pi(\frac{\lambda}{2\pi})^3 }
The effect of damping is to give the refractive index an imaginary (absorptive) part. Replace
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta' = \delta/(\gamma/2) }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\Gamma}{2\delta}\rightarrow \frac{\Gamma}{\delta}(\frac{-1}{\delta'+i})=\frac{\Gamma}{\delta}[\frac{i} }
where the first term in brackets corresponds to dispersion and the second to absorption.
- Failed to parse (syntax error): {\displaystyle e^{ikz}=e^{in_{r}\frac{\omega}{c}z}=e^{-\frac{D_0}{2}[\frac{1}{1+\delta'^2}-\frac{i\delta'}{1+delta'^2}] }
The optical density on resonance is:
Note: When the linewidth is determined by spontaneous emission then
the maximum phase shift is at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta' = \pm 1}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi = \mp \frac{D_0}{4} }









![{\displaystyle =2{\rm {Re}}[\langle n^{(0)}|d|n^{(1)}\rangle ]=2e^{2}{\rm {Re}}{\left[\sum _{s,m}{\frac {\langle n^{(0)}|s|m\rangle \langle m|z|n^{(0)}\rangle }{E_{m}-E_{n}}}\right]}{\hat {s}}\cdot {\hat {z}}{\mathcal {E}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afd33952a21990436ab03840a4b4e1e286b70684)
































































































![{\displaystyle {\begin{array}{rcl}a_{k}^{(1)}(t)&=&(i\hbar )^{-1}\int _{0}^{t}dt^{\prime }\langle k|H^{\prime }(t^{\prime })|g\rangle e^{i\omega _{kg}t^{\prime }}\\&=&-(i\hbar )^{-1}\langle k|{\hat {e}}\cdot D|g\rangle {\frac {\mathcal {E}}{2}}\int _{0}^{t}dt^{\prime }{\left[e^{i(\omega _{kg}+\omega )t^{\prime }}+e^{i(\omega _{kg}-\omega )t^{\prime }}\right]}\\&=&{\frac {\mathcal {E}}{2\hbar }}\langle k|{\hat {e}}\cdot D|g\rangle {\left[{\frac {e^{i(\omega _{kg}+\omega )t}-1}{\omega _{kg}+\omega }}+{\frac {e^{i(\omega _{kg}-\omega )t}-1}{\omega _{kg}-\omega }}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d5e4872c67deeb9e95cc30b7f74ecd1122ce0f)



![{\displaystyle {\begin{array}{rcl}\langle D(\omega ,t)\rangle &=&2{\rm {Re}}{\left\{\langle g|{\bf {D}}|\sum _{k}a_{k}^{(1)}(t)e^{-i\omega _{kg}}|k\rangle \right\}}\\&=&{\mathcal {E}}{\rm {Re}}{\left[\sum _{k}{\frac {\langle g|D|k\rangle \langle k|{\hat {e}}\cdot D|g\rangle }{\hbar }}{\left\{{\frac {e^{i\omega t}}{\omega _{kg}+\omega }}+{\frac {e^{-i\omega t}}{\omega _{kg}-\omega }}\right\}}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bd4119db9415e85baec8331b26488d24624bfc)














![{\displaystyle [r_{j},p_{k}]=i\hbar \delta _{jk}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47639ff8ac69b050c5dc9d8cf58f9c6d17af6a3)







![{\displaystyle {1+\delta '^{2}}-{\frac {\delta '}{1+delta'^{2}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0e44366f1286094105a2fc99ae9ceb744f0efba)


![{\displaystyle \phi =-{\frac {D_{0}}{2}}{\frac {\delta '}{1+delta'^{2}}}];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb40d08119f0336e1af34196d33b493e00601617)