Quantum computation and trapped ions
Contents
Ion traps and quantum information
Quantum computation and trapped ions
A fundamental concept in Computer Science is the idea of an inherent mathematical complexity of a problem, quantified in terms of how many elementary steps are necessary to obtain a solution. This concept has been meaningful because a problem's complexity can be shown to be broadly invariant with respect to details of the apparatus or steps employed to solve the problem. However, quantum physics strikes at the heart of this thesis, by providing a new way to solve certain problems. Apparently, fewer elementary steps may be required on a quantum machine, compared with machines obeying classical physics alone. This disturbing clash breaks an elegant separation between Physics and computational complexity, and suggests that something is amiss with either the foundations of Computer Science, or the reality of computation using quantum physics. In this section, we provide perspective on the challenge quantum computation provides to Computer Science, describe several physical models of quantum computation, and present two trapped ion realizations of basic quantum gates. These results, together with the observation that quantum computation can be robust even in the presence of finite noise, support the idea that quantum computation, even with a large number of gates and quantum bits, may be physically realistic.
Quantum computation in perspective
How many elementary mathematical steps are needed to solve a problem? Consider the following examples:
%%
[2.5ex] \parbox[t]{2.5in}{\raggedright [5.5ex] \parbox[t]{2.5in}{\raggedright Multiply two matrices } [3.5ex] \parbox[t]{2.75in}{\raggedright Given a list of numbers, does any subset sum to zero? Example: has } [5.5ex] Given -bit number , is prime? [3.5ex] \parbox[t]{2.5in}{\raggedright Does an -bit number have a prime factor ?}
Problem Number of steps Add two -bit numbers Multiply two -bit numbers} \parbox[t]{2.5in}{\raggedright using primary school method; using Sh\"onhage-Strassen method}
\parbox[t]{2.5in}{\raggedright using standard method; using Coppersmith-Winograd method}
\parbox[t]{2.5in}{\raggedright using 1974 algorithm; solution is easy to verify}
\parbox[t]{2.5in}{\raggedright using naive method; using AKS method of 2002}
\parbox[t]{2.5in}{\raggedright best known today; solution is easy to verify}
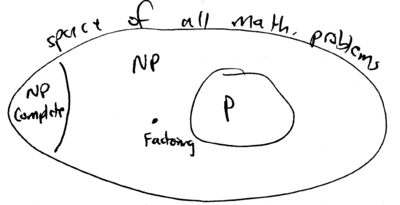
These examples illustrate a natural separation between two kinds of problems: those whose solution can be obtained in a number of steps which grows polynomially with the size of the problem, and those which seem to require an exponential number of steps to reach a decision, but are easily verified. The former are classified as P, and the latter are NP ("nondeterministic polynomial") problems. Illustrating the space of these mathematical problems as follows, one can show that P problems are contained within the class of {\bf NP} problems; moreover, there is a subset of NP-complete problems known to be the hardest of these, such that fast solution of any NP-complete problem would allow fast solution of any other {\bf NP} problem.
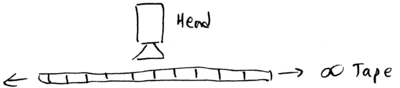
Today, the boundary between P and NP problems is increasingly becoming well defined, but it remains to be proven that PNP; this is one of the major outstanding problems in Computer Science. Conceptually, these classifications rely on a premise known as Church's Thesis, which, in modern terms, may be stated as \begin{quote} Church's Thesis: Any algorithmic process can be simulated with polynomial resource overhead, using a Turing machine. \end{quote} A Turing machine is a standardized universal computer, conceptually realized with an infinitely long, bi-directional tape, off of which data is accessed, and written by a local head. The head also controls motion of the tape; it contains a finite state machine, with a fixed amount of memory:
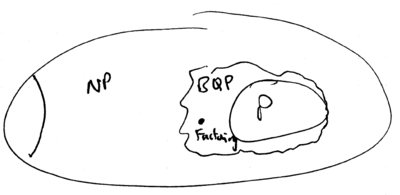
Essential to Church's Thesis is the contention that the complexity of a given mathematical problem is a fact which is independent of the Physics of the machine used. This is where quantum computation enters, because apparently, problems such as factoring (eg deciding whether has a factor less than ), are not in P (as far as is known today), if the Turing machine is constrained to use only classical laws of motion. However, if quantum physics is permitted, the problem can be solved in polynomial time. The class of problems which can be solved, with bounded error, in polynomial time, with a quantum Turing machine, is known as BQP. This class includes P, and today is believed to extend further and include problems outside of P:
Naturally, one of the central issues arising from this realization is the question: Is quantum computation real? Imagine, for example, that there were some law of Physics which placed an absolute maximum on the number of qubits which could be simultaneously entangled. This limit would need to be one of principle, rather than of practice. If such an in-princple limit existed, then quantum computers of arbitrary size would not be possible, thus allowing a sufficiently large classical computer to simulate the quantum machine with polynomial overhead. Then, with this conjectured law of Physics, BQP could become equal to P, rendering meaningless this distinction of quantum versus classical computation (and meanwhile, reducing factoring to a problem in P). On the other hand, if realistic prescriptions for arbitrarily large quantum computers can be given, and no new principles of Physics are found which are inconsistent with their realization, then the foundations of Computer Science would have to be revised. Thus, in the spirit of determining the reality of quantum computation, it is interesting to consider how they might be realized, for example, using trapped ions.
Models of quantum computation
Universal quantum computers can be realized using several models, which differ importantly in the physical resources called for. The most widely prescribed resource set for realizing a quantum computer, known as DiVincenzo's Criteria, require: \begin{itemize}
- Individually addressable qubits, with
- Arbitrary unitary transforms
- Initial state preparation of
- Projective measurement in the computational basis
\end{itemize} These requirements are based on the idea of building a {\em quantum circuit} from basic elements, quantum gates, following the theorem that \begin{quote} Theorem: Any -qubit unitary transform can be constructed from single qubit gates and two-qubit controlled-{\sc not} gates. \end{quote} Single qubit gates are typically realized, with trapped ion qubits, using laser pulses which perform rotations on the Bloch spheres representing two-level pairs of internal states. The {\sc cnot} gate captures the need for interactions between qubits; it is representative, and not specifically required. The unitary transform implemented by a {\sc cnot} is , where represents binary addition modulo two. It is equivalent to a controlled- gate, also known as a {\sc cphase} gate, up to two Hadamard gates:
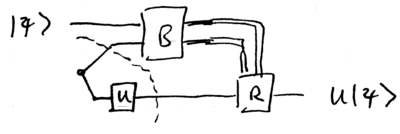
\noindent The quantum circuit model can thus be said to require state qubits, a family of small quantum gates from which arbitrary can be constructed, and projective measurements in the , basis. The teleportation model of quantum computation uses the fact that certain gates can be embedded inside an entangled state, using this circuit:
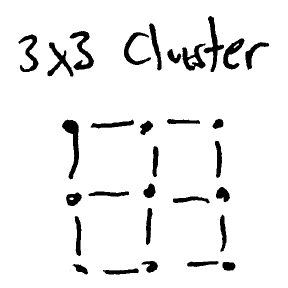
\noindent Here, represents a projective measurement in the Bell basis ( and ), and the "" on the bottom left denotes an entangled state on half of which is performed. With the appropriate recovery operation , selected from just two gates, and , the output state can be , for input , and for certain . Thus, this model of quantum computation asks for Bell basis measurements, and gates, and a supply of appropriately entangled states. Another model is given by measurement-based quantum computation, which starts with a specific entangled "cluster" state, for example a square grid of qubits
\noindent in which nearest neighbors are coupled by application of a {\sc cphase} gate. Alternatively, this initial cluster state could possibly be created by evolving a system of coupled spins into the ground state of some Hamiltonian. Quantum computations are then performed by measuring individual qubits in varying bases. These measurements proceed sequentially, for example, from left to right, with earlier measurement results determining the basis used to subsequent measurements. Thus, this model of quantum computation requires an initial "cluster" entangled states, and single qubit measurements in arbitrary bases. The quantum circuit model is appealing to a wide range of physical implementations, because the most difficult element to realize is a two-qubit gate such as the {\sc cnot} or {\sc cphase}. The teleportation model is used particularly in quantum computation with linear optics, partly due to the ease with which entangled photon pairs can be created, and mainly due to the ability to separate gates from qubits containing data until the right time. The measurement based model has been applied to optical qubits, but is mostly likely of future interest to schemes such as optical lattices of atoms, which can naturally realize the requisite entangled cluster state. Clearly, it helps to choose the model which best matches naturally available resources for realistic experimental realization of quantum computation.
The Cirac-Zoller gate
Let us now consider how the {\sc cnot} gate could be realized with qubits represented by trapped ions. Suppose we have an idealized system of two trapped ions, confined together in single one-dimensional harmonic potential, sharing a common center-of-mass vibrational mode of frequency , much like a single molecule:
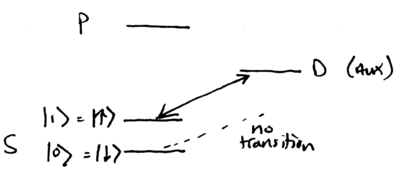
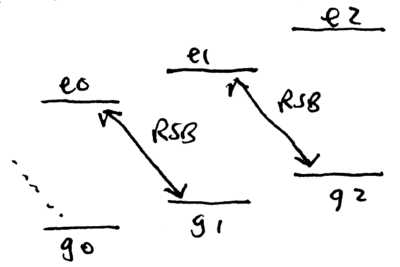
Let the qubits be represented by spin states in the level of the ion, and suppose the ion has an additional "auxiliary" level (which could be another level, or something in the state manifold), that is selectively accessible by an optical transition from :
The red sideband of this transition from to couples to , but not :
\noindent Recall that for a rotation operator
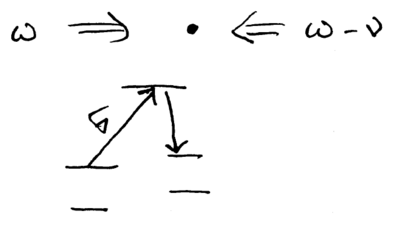
a pulse flips the qubit, since , but a pulse leaves it with an overall sign, since . Thus, a pulse on the red sideband of the transition from to , assuming the motion starts in the state, results in the transform
This is the unitary transform of the {\sc cphase} gate. A controlled-phase gate can thus be realized between the two ions by initializing the shared center-of-mass phonon state to , swapping a qubit from ion 2 into the phonon, performing the {\sc cphase} gate just described with pulses on ion 1, then swapping the phonon back into ion 2. Swapping the phonon and internal state can be done using a pulse on the red sideband of the carrier transition:
Thus, the overall procedure for this Cirac-Zoller gate is:
This implements a {\sc cphase} gate, from which a {\sc cnot} can be obtained by prepending and post-pending Hadamard gates on the target qubit. The major limitations of this scheme are that (1) the phonon state must be initialized to , so that good resolved sideband cooling is necessary, and (2) the speed of the gate is limited to , due to the pulse widths required for the sideband excitations.
The geometric phase gate
Some of the limitations of the Cirac-Zoller gate can be circumvented using a different method for realizing a {\sc cphase} gate, based on geometric phases. Recall that using a "moving standing wave," a state dependent force which maps and can be realized:
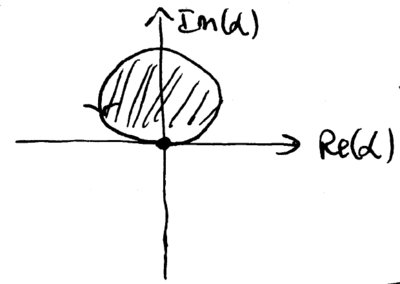
\noindent This implements a displacement operator on the phonon mode. Two back-to-back displacements give
where the extra phase factor comes from the path enclosing some area in the phase space of the , plane. Conceptually, this extra phase could be used to provide a qubit state selective phase, if the phonon state is displaced in a path which starts from and returns to the same point in phase space. For example, displacements could be arranged to move the phonon around a circle, with the area selected to map and :
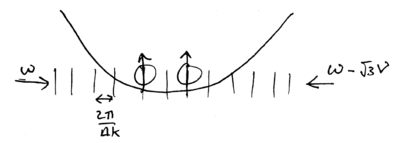
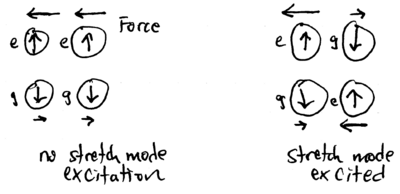
Furthermore, this idea can be generalized to impart a state-selective phase to two ions, in the following way. Consider two ions in a moving standing wave of detuning , such that the frequency center-of-mass mode is left unexcited, and but the frequency stretch mode is excited:
Specifically, suppose that the force is imparted by a laser beam selected to act on but not on , so that if the internal state is the force is large, and if the internal state is the force is small. These forces thus do not excite the stretch mode if both ions are in the same state, either or . However, if the ions have opposite spin, either or , then the differential force between the two ions excites their stretch mode:
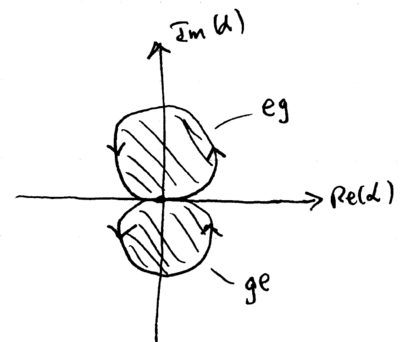
Applying a force tuned to displace the two ions around a circle in phase space can thus give a selective phase factor of to and , while leaving and with no phase change:
This implements the unitary transform
where the equality is up to an overall (and irrelevant) global phase factor. Adding two single qubit rotations gives a controlled-{\sc phase} gate:
- Failed to parse (syntax error): {\displaystyle R_{z1}(\pi/2) R_{z2}(\pi/2) U = \mbox{\sc cphase} \,, }
and adding two additional Hadamard gates gives a {\sc cnot}.
Quantum computation with noisy gates
How robust is quantum computation in the presence of noise? It turns out a similar question was asked about classical computers, early in their history. This motivated John von Neumann to study the possibility of the synthesis of reliable organisms from unreliable parts, and inspired by biological systems, he proved a theorem which has evolved into the following: \begin{quote} Theorem: A circuit containing error-free gates can be simulated with probability of error less than , using faulty gates, which fail with probability at most , as long as is less than some threshold . \end{quote} Note that the failure probability threshold is {\em independent} of the circuit size , and the desired reliability . This is because is actually determined, in principle, by properties of error correction codes, not by the ideal system being simulated. For classical circuits and using classical error correction codes, can be as high as . Today, an analogous theorem which applies to quantum circuits is known. However, because of the additional kinds of errors which can happen to qubits, versus bits, quantum error correction codes are correspondingly more complex, and thus for quantum computation is believed to be in the range of to perhaps . The fact that such thresholds even exist is remarkable, for quantum computation. Their existence implies that below a certain, constant level of noise, arbitrarily large quantum computations can be performed with a resource overhead which grows very slowly with respect to the size of the computational task. Even more remarkably, gate error probabilities of may not be unreasonable for realistic implementations of quantum computers, such as trapped ions. This can be seen from careful analysis of the Cirac-Zoller and geometric phase gates, for example, in which the coherence of the intermediate phonon state is the most limiting element. Careful experiments should thus be done to quantify achievable coherence times, and to predict eventual quantum gate error probabilities with reasonable extrapolations about technological capabilities for systems with large numbers of qubits.
























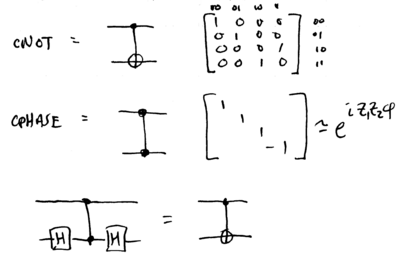



















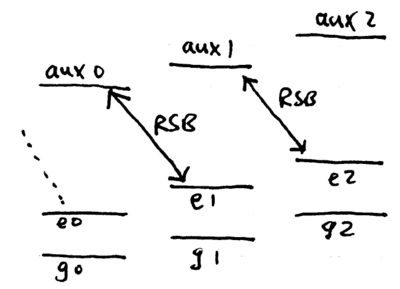








![{\displaystyle {\begin{array}{rcl}{\rm {initialize}}&\rightarrow &(a|g{\rangle }+b|e\rangle )(c|g{\rangle }+d|e\rangle )|0{\rangle }\\{R_{eg2}^{RSB}(\pi )}&\rightarrow &(a|g{\rangle }+b|e\rangle )|g\rangle (c|0{\rangle }+d|1\rangle )\\{R_{aux1}^{RSB}(2\pi )}&\rightarrow &ac|gg0\rangle +ad|gg1\rangle +bc|eg0{\rangle }-bd|eg1{\rangle }\\{R_{eg2}^{RSB}(\pi )}&\rightarrow &\left[{ac|gg\rangle +ad|ge\rangle +bc|eg{\rangle }-bd|ee\rangle }\right]|0{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/430af4eeda014f61f4ed80a81982766236eb58d4)
















![{\displaystyle U=\left[{\begin{matrix}1&0&0&0\\0&i&0&0\\0&0&i&0\\0&0&0&1\\\end{matrix}}\right]\approx e^{i(\pi /4)\sigma _{z1}\sigma _{z2}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdfd0b119f547fe928c36606adada26518bddd69)







