Now, unlike in classical mechanics, most resonances studied in atomic physics
are not harmonic oscillators, but two-level systems. Unlike harmonic
oscillators, two-level systems show saturation. When a harmonic oscillator is
driven longer or faster, higher and higher excited states are populated: the
oscillator amplitude can become arbitrarily large. In contrast, the amplitude
of oscillation in a two-level system is limited to one half in the appropriate
dimensionless units.\footnote{An analogous dimensionless amplitude for the
harmonic oscillator would be the amplitude measured in units of the oscillator
ground state size.}
Why, and under what conditions, do classical harmonic oscillator models of a
two-level system work? A two-level system of energy difference  can be
approximated by a harmonic oscillator of frequency
can be
approximated by a harmonic oscillator of frequency  when saturation effects in the two-level system are negligible, i.e. when the
population of the second excited state in the harmonic oscillator problem is
negligible, or equivalently when the population ratio of the first excited state
to the the ground state is small:
when saturation effects in the two-level system are negligible, i.e. when the
population of the second excited state in the harmonic oscillator problem is
negligible, or equivalently when the population ratio of the first excited state
to the the ground state is small:  . This is the basis for
the classical Lorentz model of the electron bound in the atom that describes
many linear atomic properties (for instance the refractive index) very well.
See "The origin of the refractive index" in chapter 31 of the Feynman
Lectures on Physics \cite{Feynman1963}.
When saturation comes into play, i.e. when the initial ground state is
appreciably depleted, the harmonic oscillator ceases to be a good model. The
limit on the oscillation amplitude in a two-level system suggests that a
classical system with periodic evolution and a limit on the amplitude, namely
rotation, could provide a better classical model of a two-level system. Indeed,
the motion of a classical magnetic moment in a uniform field provides a model
that captures almost all features of the quantum-mechanical two-level system,
the exception beting the projection onto one of the two possible outcomes in a
measurement.
\section{Magnetic Resonance: The Classical Magnetic Moment in a Spatially
Uniform Field}
. This is the basis for
the classical Lorentz model of the electron bound in the atom that describes
many linear atomic properties (for instance the refractive index) very well.
See "The origin of the refractive index" in chapter 31 of the Feynman
Lectures on Physics \cite{Feynman1963}.
When saturation comes into play, i.e. when the initial ground state is
appreciably depleted, the harmonic oscillator ceases to be a good model. The
limit on the oscillation amplitude in a two-level system suggests that a
classical system with periodic evolution and a limit on the amplitude, namely
rotation, could provide a better classical model of a two-level system. Indeed,
the motion of a classical magnetic moment in a uniform field provides a model
that captures almost all features of the quantum-mechanical two-level system,
the exception beting the projection onto one of the two possible outcomes in a
measurement.
\section{Magnetic Resonance: The Classical Magnetic Moment in a Spatially
Uniform Field}
Magnetic Moment in a Static Field
The interaction energy of a magnetic moment  with a magnetic field
with a magnetic field
 is given by
is given by

In a uniform field the force

vanishes, but the torque

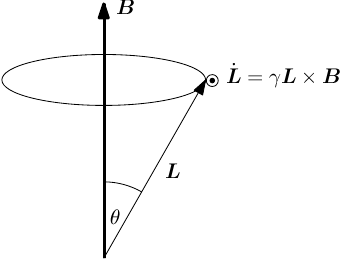
does not. For an angular momentum  the equation of motion is then
the equation of motion is then

where we have introduced the gyromagnetic ratio  as the proportionality
constant between angular momentum and magnetic moment, as shown in Figure
\ref{fig:static_precession}.
\begin{figure}
as the proportionality
constant between angular momentum and magnetic moment, as shown in Figure
\ref{fig:static_precession}.
\begin{figure}
\caption{Precession of a the magnetic moment and associated angular momentum
about a static field  .}
.}
\end{figure}
This describes the precession of the magnetic moment about the magnetic field
with angular frequency

 is known as the Larmor frequency.
For electrons we have Failed to parse (unknown function "\unit"): {\displaystyle \gamma_e=2\pi\times\unit{2.8}{\mega\hertz\per G}}
,
for protons Failed to parse (unknown function "\unit"): {\displaystyle \gamma_e=2\pi\times\unit{4.2}{\kilo\hertz\per G}}
.
is known as the Larmor frequency.
For electrons we have Failed to parse (unknown function "\unit"): {\displaystyle \gamma_e=2\pi\times\unit{2.8}{\mega\hertz\per G}}
,
for protons Failed to parse (unknown function "\unit"): {\displaystyle \gamma_e=2\pi\times\unit{4.2}{\kilo\hertz\per G}}
.
An Alternative Solution: Rotating Coordinate System
A vector  rotating at constant angular velocity
rotating at constant angular velocity  is
described by
is
described by

Then the rates of change of  measured in a coordinate system rotating
at
measured in a coordinate system rotating
at  and in an inertial system are related by
and in an inertial system are related by

This follows immediately from the following facts:
\begin{itemize}
* If  is constant in the rotating system then
is constant in the rotating system then
 .
.
* If  then
then
 .
.
* Coordinate rotation is a linear transformation.
\end{itemize}
This transformation is sometimes abbreviated as the schematic rule

It follows that the angular momentum
in a rotating frame obeys

If we choose  , then
, then
 is constant in the rotating frame. Often it is useful to
think of a fictitious magnetic field
is constant in the rotating frame. Often it is useful to
think of a fictitious magnetic field  that appears in a rotating frame.
that appears in a rotating frame.
Larmor's Theorem for a Charged Particle in a Magnetic Field
The vanishing of the torque on a magnetic moment when viewed in the correct
rotating frame is reminiscent of Larmor's theorm for the motion of a charged
particle in a magnetic field, which we now present.
If the Lorentz force acts in an inertial frame,

then in the rotating frame, according to the rule
\ref{eqn:rot_frame_transformation} we have

resulting in a force  in the rotating frame given by
in the rotating frame given by

where we have used
 .
Choosing
.
Choosing

yields

if the  field is not too large. Thus the Lorentz force approximately
disappears in the rotating frame. Note that while the vanishing of the force is
approximate, the vanishing of the torque on a magnetic moment in the rotating
frame is an exact result.
field is not too large. Thus the Lorentz force approximately
disappears in the rotating frame. Note that while the vanishing of the force is
approximate, the vanishing of the torque on a magnetic moment in the rotating
frame is an exact result.
Rotating Magnetic Field on Resonance
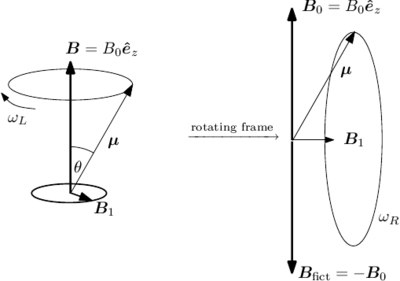
\begin{figure}
\caption{Field and moment vectors in the static and rotating frames for the case
of resonant drive.}
\end{figure}
Consider a magnetic moment  precessing about a field
precessing about a field
 with
with  in spherical coordinates, where
in spherical coordinates, where  . Assume that we now
apply an additional field
. Assume that we now
apply an additional field  , in the
, in the  -plane rotating at
-plane rotating at
 . To solve the resulting problem it is simplest to go into the
rotating frame (Figure \ref{fig:rotating_frame}). Then
. To solve the resulting problem it is simplest to go into the
rotating frame (Figure \ref{fig:rotating_frame}). Then  is
stationary, say along
is
stationary, say along  , and there is an additional fictitious
field
, and there is an additional fictitious
field  which
cancels the field
which
cancels the field  . So in the rotating frame we are left just with
the static field
. So in the rotating frame we are left just with
the static field  , and the magnetic moment precesses about
, and the magnetic moment precesses about
 at the Rabi frequency
at the Rabi frequency

A magnetic moment initially along the  axis will point along
the
axis will point along
the  axis at a time
axis at a time  given by
given by  , while a
magnetic moment parallel or antiparallel to applied magnetic field
, while a
magnetic moment parallel or antiparallel to applied magnetic field  does not precess in the rotating frame.
\QU{
Assume the magnetic moment is initially pointing
along the
does not precess in the rotating frame.
\QU{
Assume the magnetic moment is initially pointing
along the  axis. Assume that a rotating field
axis. Assume that a rotating field  is
applied, but that it rotates at a frequency
is
applied, but that it rotates at a frequency  ,
where
,
where  is the Larmor frequency for the static field
is the Larmor frequency for the static field  .
Compared to the on-resonant case,
.
Compared to the on-resonant case,  , is the oscillation frequency of
the magnetic moment.
\begin{enumerate}
, is the oscillation frequency of
the magnetic moment.
\begin{enumerate}
* larger
* the same
* smaller
\end{enumerate}
}
\QU{
Same question as \ref{q:rabi_freq_blue_detuned} but for  .
}
.
}
Rotating Magnetic Field Off-Resonance
If the rotation frequency
 of
of  does not equal the Larmor frequency
does not equal the Larmor frequency
 associated with the static field
associated with the static field  , then in
the frame rotating with
, then in
the frame rotating with  at frequency
at frequency  the static field
is not completely cancelled by the fictitious field
the static field
is not completely cancelled by the fictitious field
 , but a difference along
, but a difference along  remains,
giving rise to a total effective field in the rotating frame
remains,
giving rise to a total effective field in the rotating frame

The effective field is static, lies at an angle  with the z
with the z

and is of magnitude

The magnetic moment precesses around it with an effective (sometimes called
generalized) Rabi frequency

where  is the Rabi frequency associated with
is the Rabi frequency associated with  , and
, and
 is the detuning from resonance with the Larmor
frequency
is the detuning from resonance with the Larmor
frequency  .
\subsection{Geometrical Solution for the Classical Magnetic Moment in Static and
Rotating Fields}
\begin{figure}
.
\subsection{Geometrical Solution for the Classical Magnetic Moment in Static and
Rotating Fields}
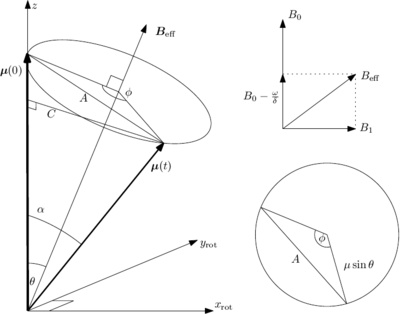
\begin{figure}
\caption{Geometrical relations for the spin in combined static and rotating
magnetic fields, viewed in the frame co-rotating with the drive field
 . At lower right is a view looking straight down the
. At lower right is a view looking straight down the
 axis.}
axis.}
\end{figure}
Referring to Figure \ref{fig:rotating_coord_construction}, we have

On the other hand

so that

With  the Larmor frequency of the static field,
the Larmor frequency of the static field,
 the detuning,
the detuning,  the resonant and
the resonant and
 the generalized Rabi frequencies. Note
that the precession is faster, but the amplitude smaller for an off-resonant
field than for the resonant case. The above result is also the correct
quantum-mechanical result.
the generalized Rabi frequencies. Note
that the precession is faster, but the amplitude smaller for an off-resonant
field than for the resonant case. The above result is also the correct
quantum-mechanical result.
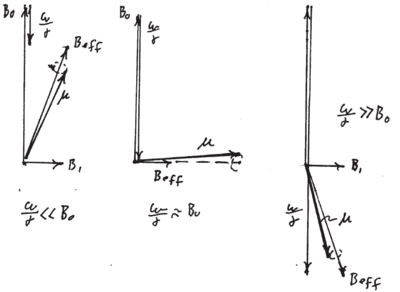
"Rapid" Adiabiatic Passage
Rapid adiabatic passage is a technique for inverting a spin by (slowly) sweeping
the detuning of a drive field through resonance. "Slowly" means slowly
compared to the Larmor frequency  about the effective
static field in the rotating frame for all times. The physical picture is as
follows. Assume the detuning is initially negative (
about the effective
static field in the rotating frame for all times. The physical picture is as
follows. Assume the detuning is initially negative ( ,
,
 ). Since
). Since

the effective magnetic field initially points of a small angle
relative to the  axis. If the detuning is increased slowly
compared to the Larmor frequency, the spin will continue to
precess tightly around
axis. If the detuning is increased slowly
compared to the Larmor frequency, the spin will continue to
precess tightly around  , which for
, which for  points
along the x axis, and for
points
along the x axis, and for  along the
along the  axis
(see Figure \ref{fig:rapid_adiabatic_passage}).
\begin{figure}
axis
(see Figure \ref{fig:rapid_adiabatic_passage}).
\begin{figure}
\caption{Motion of the spin during rapid adiabatic passage, viewed in the frame
rotating with  . The spin's rapid precession locks it to the
direction of
. The spin's rapid precession locks it to the
direction of  and thus it is dragged through an angle
and thus it is dragged through an angle  as the frequency is swept through resonance.}
as the frequency is swept through resonance.}
\end{figure}
Thus the magnetic moment, starting out along  ,
ends up pointing along
,
ends up pointing along  . Note that in the
rotating frame
. Note that in the
rotating frame  remains always (almost) parallel to the
effective field
remains always (almost) parallel to the
effective field  .
A similar precess is used in magnetic traps for atoms, but there
.
A similar precess is used in magnetic traps for atoms, but there
 is a real, spatially dependent field constant in time.
As the atom moves in this field, the fast precession of the
magnetic moment about the local field keeps its direction locked
to the local field, whose direction varies in the lab frame.
Returning to rapid adiabatic passage, since the generalized Rabi frequency is
smallest and equal to the resonant Rabi frequency
is a real, spatially dependent field constant in time.
As the atom moves in this field, the fast precession of the
magnetic moment about the local field keeps its direction locked
to the local field, whose direction varies in the lab frame.
Returning to rapid adiabatic passage, since the generalized Rabi frequency is
smallest and equal to the resonant Rabi frequency  at
at  , the
adiabatic requirement is most severe there, i.e. near
, the
adiabatic requirement is most severe there, i.e. near  .
Near
.
Near  we have, with
we have, with  ,
,

where the exclamation point in  indicates a requirement which
we impose. Consequently, if the evolution is to be adiabatic, we must have
indicates a requirement which
we impose. Consequently, if the evolution is to be adiabatic, we must have
 .
This means that the change
.
This means that the change  of rotation frequency
of rotation frequency
 per Rabi period
per Rabi period  ,
,
 ,
must be small compared to the Rabi frequency
,
must be small compared to the Rabi frequency  . The quantum mechanical
treatment yields a probability for non-adiabatic transition (probability for the
magnetic moment not following the magnetic field) given by
. The quantum mechanical
treatment yields a probability for non-adiabatic transition (probability for the
magnetic moment not following the magnetic field) given by

in agreement with the above qualitative discussion.