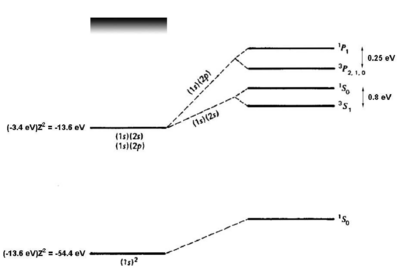
Energy Levels of Helium
Energy Levels of Helium
\caption{Energy levels of helium. Figure adapted from Gasiorowicz \cite{Gasiorowicz}. The quantum mechanics texts of Gasiorowicz and Cohen-Tannoudji \cite{CohenT} are valuable resources for more detailed treatment of the helium atom.}
If we naively estimate the binding energy of ground-state helium () as twice the binding energy of a a single electron in a hydrogenic atom with , we obtain . Comparing to the experimental result of 79 eV, we see a \textit{big} (39 eV) discrepancy. However, we have neglected the interaction. Introducing a perturbation operator
where is the distance between the two electrons, and still approximating each electron to be in the state---yielding a total wavefunction ---we obtain the first-order correction
which removes most of the discrepancy. A single-parameter variational ansatz using as parameter removes of the remaining discrepancy. Thus, although we cannot solve the helium Hamiltonian exactly, we can understand the ground -state energy well simply by taking into account the shielding of the nuclear charge by the interaction. For the first excited states, there are two possible electronic configurations, and . The electron sees a shielded nucleus ( vs. ) due to the electron, and consequently has a smaller binding energy, comparable to the binding energy for hydrogen ( eV). For the electron, which has no node at the nucleus, the shielding effect is similar but weaker (see figure \ref{fig:he_levels}). Consider now the possible terms for the configuration: \begin{itemize}
- (singlet)
- (triplet)
\end{itemize} The singlet and triplet states are, respectively, antisymmetric and symmetric under particle exchange. Since Fermi statistics demand that the total wavefunction of the electrons be antisymmetric, the spatial and spin wavefunctions must have opposite symmetry,
Here, is the wavefunction with symmetric spatial part and antisymmetric spin state , i.e. the spin singlet (S=0, term). is the wavefunction with antisymmetric spatial part and symmetric spin state , i.e. the spin triplet (S=1, term). Now consider the Coulomb energy of the interaction in these excited states:
The first term (called the Coulomb term, although both terms are Coulombic in origin) is precisely what we would calculate classically for the repulsion between two electron clouds of densities and . The second term, the exchange term, is a purely quantum mechanical effect associated with the Pauli exclusion principle. The triplet state has lower energy, because the antisymmetric spatial wavefuntion reduces repulsion interactions. Since the interaction energy is spin-dependent, it can be written in the same form as a ferromagnetic spin-spin interaction,
To see this, we use the relation . Since , eq. \ref{eq:ferro} is equivalent to
where we have substituted for the singlet and triplet states, respectively. Bear in mind that, although the interaction energy is spin-dependent, the origin of the coupling is electrostatic and not magnetic. Because of its electrostatic origin, the exchange energy (0.8 eV for the splitting, as indicated in figure \ref{fig:he_levels}) is much larger than a magnetic effect such as the fine structure splitting, which carries an extra factor of . \begin{figure}
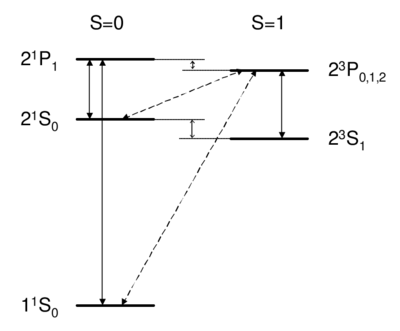
\caption{Dipole-allowed transitions (solid) and intercombination lines (dashed) in helium.}
\end{figure}
What field (coupling) drives singlet-triplet transitions?
A. Optical fields (dipole operator)
B. rotating magnetic fields
C. Both
D. None
Singlet-triplet transitions are forbidden by the selection rule, so to first order the answer is D. A is ruled out because the dipole operator acts on the spatial wavefunction, not on the spin part. One might think (B) that a transverse magnetic field, which couples to , , can be used to flip a spin. However, a transverse field can only rotate the two spins together; it cannot rotate one spin relative to the other, as would be necessary to change the magnitude of . Because all spin operators are symmetric against particle exchange, they couple only . Thus, spatial and spin symmetry (S,A) are both good quantum numbers. More formally, if all observables commute with the particle exchange operator , then (S or A) is a good quantum number. Thus, as long as wavefunction and operators separate into spin dependent and space dependent parts , both 's are conserved. Intercombination (i.e. transition between singlet and triplet) is only possible when this assumption is violated, i.e. when the spin and spatial wavefunctions are mixed, e.g. by spin orbit coupling. As we will see in Ch. \ref{ch:fs}, spin orbit coupling is , and hence is weak for helium. Thus, the state of helium is \textit{very} long-lived, with a lifetime of about 8,000 s. (footnote: Historically, the absence of transition between singlet and triplet states led to the belief that there were two kinds of helium, ortho-helium (triplet) and para-helium (singlet).) The other noble gases (Ne, Ar, Kr, Xe) have lifetimes on the order of 40 s. Because they are so narrow, intercombination lines are of great interest for application in optical clocks. While a lifetime of 8000 s is \textit{too} long to be useful (because such a narrow transition is difficult both to find and to drive), intercombination lines in Mg, Ca, or Sr---with linewidths ranging from mHz to kHz---are discussed as potential optical frequency standards \cite{Ludlow2006, Ludlow2008}.




























![{\displaystyle {\begin{aligned}\Delta E&={\frac {1}{2}}\int \int {\frac {e^{2}}{r_{12}}}[|\psi _{100}(r_{1})|^{2}|\psi _{200}(r_{2})|^{2}+(r_{1}\leftrightarrow r_{2})]\\&\pm {\frac {1}{2}}\int \int {\frac {e^{2}}{r_{12}}}[\psi _{100}^{*}(r_{1})\psi _{200}^{*}(r_{2})\psi _{100}(r_{2})\psi _{200}(r_{1})+(r_{1}\leftrightarrow r_{2})]\\&=\Delta E^{Coul}\pm \Delta E^{exch}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f7da0a65ae741e23636787881de55fc50acbe4a)
















![{\displaystyle [P_{ij},{\hat {O}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d769b158d5a631785fbe3e4a49023eeb2ea0cabd)



