Fine structure in applied magnetic fields
In this section we treat the interaction of the electron's orbital
and spin angular momentum with external static magnetic fields.
Previously, in the chapter on fine structure, we have considered
the spin-orbit interaction: the coupling of electron spin to the
magnetic field generated by the nucleus (which appears to move
about the electron in the electron's rest frame). The spin orbit
interaction causes the orbital and spin angular momenta of the
electron to couple together to produce a total spin which then
couples to the external field; the magnitude of this coupling is
calculated here for weak external fields.
We first discuss the magnetic moment due to orbital angular momentum and spin angular momentum, and then we put things together.
Magnetic moment of circulating charge (classical)
The energy of interaction of a classical magnetic moment
 with a magnetic field
with a magnetic field  is
is

indicating that the torque tends to align the moment along the
field. In classical electrodynamics the magnetic moment of a
moving point particle about some point in space is independent of
the path which it takes, but depends only on the product of the
ratio of its charge to mass  , and angular momentum
, and angular momentum  .
This result follows from the definitions of angular momentum
.
This result follows from the definitions of angular momentum
![{\displaystyle {\bf {L}}\equiv {\bf {r}}\times {\bf {p}}=m[{\bf {r}}\times {\bf {v}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec2eddb604bfaa8fd59d39605c478c24e75b46e)
and magnetic moment
![{\displaystyle {\bf {\mu }}\equiv {\frac {1}{2}}{\bf {r}}\times {\bf {i}}={\frac {q}{2}}[{\bf {r}}\times {\bf {v}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aaadcf4f4cf0a3b5f7ab0f58413a6f6e0b1c6a2)
where  is the current and
is the current and  the velocity (see Jackson
Ch.5). The equality of the bracketed terms implies
the velocity (see Jackson
Ch.5). The equality of the bracketed terms implies

where  is referred to as the \emph{gyromagnetic
ratio}. This is a general result for any turbulently rotating blob
provided only that it has a constant ratio of charge to mass
throughout.
For an electron with orbital angular momentum
is referred to as the \emph{gyromagnetic
ratio}. This is a general result for any turbulently rotating blob
provided only that it has a constant ratio of charge to mass
throughout.
For an electron with orbital angular momentum 

which is the classical result, and  is the \emph{Bohr
magneton}:
is the \emph{Bohr
magneton}:
- Failed to parse (unknown function "\unit"): {\displaystyle \mu_B = \frac{e\hbar}{2m} = \unit{9.27408(4)\times 10^{-24}}{\joule\per\tesla} \rightarrow \unit{1.39983 \times 10^4}{\mega\hertz} \times B/(\text{Tesla}) }
Intrinsic electron spin and magnetic moment
When Uhlenbeck and Goudsmit suggested \cite{Uhlenbeck1926} that the
electron had an intrinsic spin  , it soon became
apparent that it had a magnetic moment twice as large as would be
expected on the basis of the treatment above. (This implies
that the electron cannot be made out of material with a uniform
ratio of charge to mass.) This is accounted for by writing for the
intrinsic electron moment
, it soon became
apparent that it had a magnetic moment twice as large as would be
expected on the basis of the treatment above. (This implies
that the electron cannot be made out of material with a uniform
ratio of charge to mass.) This is accounted for by writing for the
intrinsic electron moment

where the quantity  is called the electron
is called the electron  -factor.
(The negative sign permits treating
-factor.
(The negative sign permits treating  as a
positive quantity, which is the convention.)
This factor was predicted by the Dirac theory of the electron,
probably its greatest triumph.
Later, experiments by Kusch, followed by Crane et al., and then by Dehmelt and
coworkers, have shown (for both electrons and positrons).
as a
positive quantity, which is the convention.)
This factor was predicted by the Dirac theory of the electron,
probably its greatest triumph.
Later, experiments by Kusch, followed by Crane et al., and then by Dehmelt and
coworkers, have shown (for both electrons and positrons).

This result has been calculated from quantum electrodynamics, which
gives

The agreement betwen the prediction of quantum electrodynamics and experiment on
the electron g-factor is often cited as the most precise test of theory in all
of physics.
The Lande g-factor
In zero or weak magnetic field, the Hamiltonian is

Since the second term (LS coupling) corresponds to an internal B field of about one Tesla, we will consider the limit of a weak external magnetic field.
The spin orbit interaction couples  and
and  together to form
together to form  . For the Zeeman Hamiltonian, we therefore have to project all angular momenta and the magnetic field along the direction of
. For the Zeeman Hamiltonian, we therefore have to project all angular momenta and the magnetic field along the direction of  :
:

We want to write this as

which defines the so-called Lande g factor  .
.
The interaction of the field is actually with  and
and
 , however
, however  is not simply related to these
quantities because
is not simply related to these
quantities because  and
and  precess
about {
precess
about {  } instead of the field. As Land\'{e} showed in
investigations
of angular momentum coupling of different electrons \cite{Lande1923},
it is a simple matter to find
} instead of the field. As Land\'{e} showed in
investigations
of angular momentum coupling of different electrons \cite{Lande1923},
it is a simple matter to find  by calculating the sum of the
projections of
by calculating the sum of the
projections of  and
and  onto {
onto {  }.
The projection of
}.
The projection of  on {
on {  } is
} is

The projection of  on {
on {  } is
} is

The definition of  gives
gives

Taking 

using  .
If a transition from a level with angular momentum
.
If a transition from a level with angular momentum  to
a level with
to
a level with  takes place in a magnetic field, the resulting spectral line will
be split into three or more components---a phenomenon known as the
Zeeman effect. For transitions with a particular
takes place in a magnetic field, the resulting spectral line will
be split into three or more components---a phenomenon known as the
Zeeman effect. For transitions with a particular  ,
say
,
say  , the components will have shifts
, the components will have shifts
![{\displaystyle \Delta E_{z,m,-1}={\left[g_{j^{\prime }}m-g_{j^{\prime \prime }}(m-1)\right]}\mu _{B}B={\left[(g_{j^{\prime }}-g_{j^{\prime \prime }})m-g_{j^{\prime \prime }}\right]}\mu _{B}B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d5db3f438ad77862cfde1c87a01e4c2f17232b)
If  (or if
(or if  or
or  )
then
)
then  will not depend on
will not depend on  (or there will be
only one transition with
(or there will be
only one transition with  ) and there will be only 3
components of the line (
) and there will be only 3
components of the line ( ); this is called the
normal Zeeman splitting. If neither of these conditions holds, the
line will be split into more than 3 components and the Zeeman
structure is termed "anomalous"---it can't be explained with
classical atomic models.
); this is called the
normal Zeeman splitting. If neither of these conditions holds, the
line will be split into more than 3 components and the Zeeman
structure is termed "anomalous"---it can't be explained with
classical atomic models.
Hyperfine structure in an applied field
The Hamiltonian in an applied field  is
is

By convention, we take  . Note
that we are expressing the nuclear
moment in terms of the Bohr magneton, and that
. Note
that we are expressing the nuclear
moment in terms of the Bohr magneton, and that  . (The
nuclear moment is often expressed
in terms of the nuclear magneton, in which case
. (The
nuclear moment is often expressed
in terms of the nuclear magneton, in which case  =
=
 , where
, where
 is the nuclear magneton.) What are the quantum numbers and
energies? Before discussing the
general solution, let us look at the limiting cases.
is the nuclear magneton.) What are the quantum numbers and
energies? Before discussing the
general solution, let us look at the limiting cases.
Low field
The total angular momentum is  . In low
field,
. In low
field,  and
and  are good
quantum numbers. Each level
are good
quantum numbers. Each level  contains
contains  degenerate
states. In a weak field
degenerate
states. In a weak field  the (
the ( ) fold degeneracy is lifted. We can treat the terms
) fold degeneracy is lifted. We can treat the terms

as a perturbation.  and
and  are not good quantum
numbers, only their components
parallel to
are not good quantum
numbers, only their components
parallel to  are important. Thus
are important. Thus

![{\displaystyle H_{z}=-\mu _{B}{\left[-g_{j}({\bf {J}}\cdot {\bf {F}})+g_{I}({\bf {I}}\cdot {\bf {F}})\right]}{\frac {{\bf {F}}\cdot {\bf {B}}_{0}}{F^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/459cb2f712b8cb782334d0edd966919aa7075288)
Since  , we can usually neglect it. We can rewrite
this result as
, we can usually neglect it. We can rewrite
this result as


For example, let  ,
,  and
and  . Then
. Then

\begin{figure}
\centering
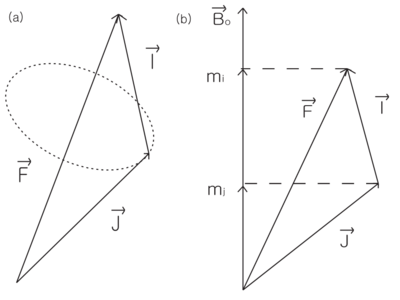
\caption{Total angular momentum F=I+J. (a) In low field, only the components of
J and I parallel to F are important. (b) In high field,  and
and  are good
quantum numbers.}
are good
quantum numbers.}
\end{figure}
High field
If  , then
{
, then
{  } is quantized along
} is quantized along
 . Although
. Although  is not
necessarily large compared to the
hyperfine interaction, the
is not
necessarily large compared to the
hyperfine interaction, the  coupling
assures that {
coupling
assures that {  } is also quantized
along
} is also quantized
along  . Thus
. Thus  and
and  are good quantum numbers.
In this case, Eq.\ \ref{EQ_hsaf1} can be written
are good quantum numbers.
In this case, Eq.\ \ref{EQ_hsaf1} can be written

The second term on the right is largest. Usually the first term is
next largest, and the nuclear
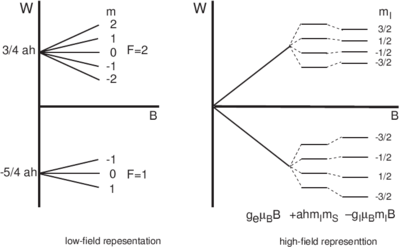
terms is smallest. Figure \ref{fig:B-field-levels} shows low and high field
behavior for hyperfine structure for  .
\begin{figure}
\centering
.
\begin{figure}
\centering
\caption{Energy level structure for a single-electron atom with nuclear spin 3/2
in the limits of low and high fields.}
\end{figure}
General solution
Finding eigenfunctions and eigenvalues of the hyperfine Hamiltonian
for arbitrary field requires
diagonalizing the energy matrix in some suitable representation.
To obtain a rough idea of the
expected results, one can smoothly connect the energy levels at low
and high field, bearing in mind
that  is a good quantum number at all fields.
For
is a good quantum number at all fields.
For  , the eigenvalues of (Eq.\ \ref{EQ_hsaf1}) can be
found exactly. The energies are
given by the Breit-Rabi formula
, the eigenvalues of (Eq.\ \ref{EQ_hsaf1}) can be
found exactly. The energies are
given by the Breit-Rabi formula

where the  sign is for
sign is for  , and the
, and the  sign is for
sign is for  .
.
 is the zero field energy separation.
is the zero field energy separation.

The parameter  is given by
is given by

Physically,  is the ratio of the paramagnetic interaction (the "Zeeman
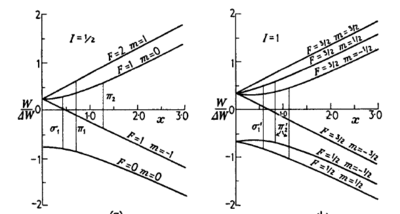
energy") to the hyperfine separation. The Breit-Rabi energy level diagram for
hydrogen and deuterium are shown in figure \ref{fig:Breit-Rabi}. The units
reflect current interest in atom trapping. Low-field quantum numbers are shown.
It is left as an exercise to identify the high field quantum numbers.
\begin{figure}
\centering
is the ratio of the paramagnetic interaction (the "Zeeman
energy") to the hyperfine separation. The Breit-Rabi energy level diagram for
hydrogen and deuterium are shown in figure \ref{fig:Breit-Rabi}. The units
reflect current interest in atom trapping. Low-field quantum numbers are shown.
It is left as an exercise to identify the high field quantum numbers.
\begin{figure}
\centering
\caption{Energy level structure for a single-electron atom with nucleaar spin I
= 1/2, such as hydrogen (left), and I = 1, such as deuterium (right). From {\it
Molecular Beams} by N.F. Ramsey \cite{Ramsey1956}.}
Notes





![{\displaystyle {\bf {L}}\equiv {\bf {r}}\times {\bf {p}}=m[{\bf {r}}\times {\bf {v}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec2eddb604bfaa8fd59d39605c478c24e75b46e)
![{\displaystyle {\bf {\mu }}\equiv {\frac {1}{2}}{\bf {r}}\times {\bf {i}}={\frac {q}{2}}[{\bf {r}}\times {\bf {v}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aaadcf4f4cf0a3b5f7ab0f58413a6f6e0b1c6a2)

































![{\displaystyle \Delta E_{z,m,-1}={\left[g_{j^{\prime }}m-g_{j^{\prime \prime }}(m-1)\right]}\mu _{B}B={\left[(g_{j^{\prime }}-g_{j^{\prime \prime }})m-g_{j^{\prime \prime }}\right]}\mu _{B}B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d5db3f438ad77862cfde1c87a01e4c2f17232b)




















![{\displaystyle H_{z}=-\mu _{B}{\left[-g_{j}({\bf {J}}\cdot {\bf {F}})+g_{I}({\bf {I}}\cdot {\bf {F}})\right]}{\frac {{\bf {F}}\cdot {\bf {B}}_{0}}{F^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/459cb2f712b8cb782334d0edd966919aa7075288)