Two-Photon Excitation
Contents
Introduction
Every radiative process described so far has involved a single photon, whether it be a hyperfine transition in magnetic resonance, optical excitation, or spontaneous emission. However, at higher power, when first-order perturbation theory breaks down, processes can occur in which an atom simultaneously absorbs two or more photons. Such multi-photon processes can lead to ionization of atoms or dissociation of molecules in intense laser fields, and phenomena such as free-to-free transitions in which an electron absorbs successive quanta as it flies out from the field of an atom.
Two-photon processes have become one of the standard tools in atomic physics
for exciting atoms to states whose energies are too high to
achieve with a single photon (e.g. Rydberg states) and also to states of the same
parity that would normally be inaccessible. In addition, a number
of ultra-high resolution (doppler-free) spectroscopic techniques are based on
two-photon processes. The ubiquitous phenomena of resonance fluorescence and Rayleigh scattering are also two-photon processes.
Our approach will be to use second-order
perturbation theory, extending the first order development used
in earlier chapters in a straightforward fashion. An alternative
approach involves solving the dynamical equations in the same
manner as we analyzed the two-level system. However, the
perturbation approach is appropriate in many cases, and is simpler
than the dynamical approach.
The aim is to cause a transition by applying two fields:
where
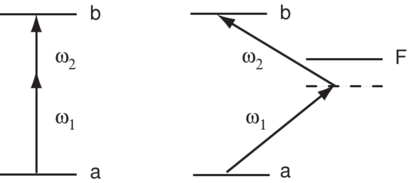
States and have the same parity, so a single photon transition is forbidden. The process is shown in Fig.~\ref{fig:two-photon}, left. A more realistic view is shown in Fig.~\ref{fig:two-photon} right, where represents some intermediate state of opposite parity. One way to describe the process is that photon causes a transition from to a "virtual" state near and the second photon at carries the system from the virtual state to the final state . The interpretation of the virtual state will be discussed in Section \ref{sec:virtual}. Note that , in reality, represents one of a complete set of eigenstates which have non-vanishing dipole matrix elements with . \begin{figure} \centering
\caption{Two-photon absorption}
\end{figure}
Calculation of the Two-Photon Rate
The Hamiltonian is of the form , where . With the field described by Eq.\ \ref{eq:introone}, we have
Defining
the matrix element is
As the counterrotating terms are usually negligible, we have dropped them for simplicity. Following the procedure used earlier, the first order solution for the amplitude of is
The second order solution for the state amplitude, , is found from
The contribution to the sum due to state is
Introducing
and defining , we have,
\noindent Eq.\ \ref{eq:ctprsix} yields
Note that the first two terms involve absorbing two photons from the same beam, while the last two involve absorbing one photon from each of the two beams. When two different frequencies are used, the first terms are invariably far from resonance and can be neglected. In the case of absorbing two photons at the same frequency, discussed below, all four terms contribute. \section{Two-photon rate with a single intermediate state} Suppose that is close to where is a particular intermediate state. In this case Eq.\ \ref{eq:ctprnine} becomes
We then obtain for the transition probability
Recalling that
we obtain
Integrating over the appropriate spectral distribution gives
We can cast the transition rate into a more familiar form by introducing the usual Rabi frequencies
Denoting the detuning of the intermediate state by
we can define the two-photon Rabi frequency by
and we have
in analogy with the expression for one-photon transitions. A more useful expression for the two-photon transition rate is in terms of the radiation intensity, . Noting that (cgs units), we have from Eq.\ \ref{eq:ctprtwo}
Eq.\ \ref{eq:ctpathree} becomes
In the case where both photons emanate from a single laser beam, equation \ref{eq:ctpasix} further simplifies to
Discussion
Applicability of one-photon results
The definition above of a two-photon Rabi frequency suggests an analogy between two-photon and one-photon transitions. The analogy is a powerful one, as many results from the study of one-photon transitions carry over to the two-photon case. These include \begin{itemize} \item{Lineshape: if the rate of spontaneous two-photon emission from to is , then the transition has Lorentzian lineshape
where is the two-photon detuning.} \item{Saturation: like single-photon transitions, two-photon transitions saturate as the rate of excitation approaches half the natural linewidth. By analogy with the one-photon case, one can define a two-photon saturation parameter .} \item{Spontaneous emission: In calculating the rate of emission, we still have , where and is the number of photons in the mode of frequency ; the two-photon emission rate thus scales as , where for every emission events in which both photons are stimulated, there is one event in which both photons are spontaneous, and there are events in which the photon in mode is stimulated and the other is spontaneous. The rate of absorption is the same as the rate of doubly-stimulated emission.} \item{The two-photon transition rate looks similar to (the rate of one-photon emission at frequency ), but is diminished by , the squared amplitude of state admixed into state .} \item{Two-photon emission: Consider the case where the population is initially in state , but there is only one laser, and its frequency is close to the transition. Then the two photon emission rate is
where is the rate of spontaneous emission from to and is the admixture of state into the initial state. This admixture may also be regarded as the "population of the virtual state." } \end{itemize}
What is the virtual state?
In calculating rates of two-photon processes, we have been making use of a "virtual" state near some intermediate state with one-photon couplings to both the initial state and the final state . We have also noted that, more generally, the virtual state can be a superposition of several states---but \textit{all} at the frequency of the drive. We can think of the virtual state purely mathematically as the thing that appears in the perturbation sum. But does it have a physical interpretation? To what extent does the transition from to occur \textit{via} ? And how can serve as an intermediate state given that the transitions into and out of apparently do not conserve energy? One interpretation is in the dressed atom picture (covered in 8.422). Because of the couplings introduced by the laser field, the true eigenstates of the system are not , , and but the so-called "dressed states." If we start with the system in and adiabatically turn on the field coupling to , the system will evolve into the dressed state . As we have seen above and will see again in the case of spontaneous Raman scattering, the rates of two-photon processes can often be understood in terms of this admixture of into , the "population of the virtual state" . Thus, one can interpret the virtual state as a component of the dressed atom wavefunction. Another way to understand the virtual state is to consider the lifetime of the atom in the intermediate state. Consider the case of two-photon emission from to via . Although a transition from to violates energy conservation by an amount , the Heisenberg uncertainty principle allows the atom to remain in the intermediate state for a time . And indeed, if one observes the emitted photons, one finds that the two photons are correlated in time to within .
Raman Processes
Stimulated Raman scattering
We have considered two-photon absorption processes, but stimulated emission can also occur as can be seen from Fig.~\ref{fig:two-photon}. \begin{figure} \centering
\caption{Raman emission. Photon can be emitted spontaneously, or by stimulated emission. }
\end{figure} In this case, the transition occurs by absorbing a photon at frequency , and emitting a photon at frequency . If the transition is stimulated by two applied radiation fields, then the process is known as stimulated Raman scattering. If , the emission is called Stokes radiation. If , the emission is called anti-Stokes radiation. In either case, the frequencies are related by
Our treatment of the two-photon transition applies, except that one interaction step corresponds to emission, rather than absorption. The change is trivial: the counter-rotating term at frequency in Eq.\ \ref{eq:ctprone}, which was dropped, is retained and the rotating term, at frequency , is dropped in its place. This merely changes the sign of in the ensuing steps, so we again obtain
where as before, but in this case
Spontaneous Raman scattering
An important aspect of Raman scattering that differentiates it from two-photon absorption is that the emission of the photon at frequency can be spontaneous. Spontaneous emission is generally too slow to be useful at low frequencies but in the optical regime the spontaneous rate can be large enough to cause a sizeable scattering signal. Initially, spontaneous Raman scattering was the only important process: not until the advent of the laser did stimulated Raman scattering became useful. We can estimate the rate of spontaneous Raman scattering by considering absorption at and emission at as separate processes, though strictly speaking only one process is involved. We start by evaluating the spontaneous emission at . This takes place from a virtual intermediate state, which we shall denote as . The spontaneous emission rate is given by the familiar expression
Next, we consider the problem of "populating" the virtual state. The rate of exciting the state can be expressed in terms of the Rabi frequency
The detuning from state is . The transition rate to the intermediate state is approximately
The time the atom can occupy the state, however, is limited by the uncertainty principle to . Hence the probability that state is occupied is roughly . Using either perturbration theory or the dressed atom picture, one can solve for the virtual state population with the correct numerical factor: . Putting the above together, we obtain the rate for spontaneous Raman scattering from to :
Since , the spontaneous Raman rate depends linearly on the power. The absorption process can be continued, allowing multi-photon Raman transitions to a final state. Note that even if a = b (i.e., if the internal state of the atom is unchanged by the two-photon transition), the final state differs from the initial state by one photon recoil. Hence, resonant fluorescence and Rayleigh scattering are Raman processes!
Two-photon Doppler-free spectroscopy
The Doppler effect is the most common source of inhomogeneous line broadening. (Inhomogeneous broadening occurs because the resonance frequencies of different atoms are shifted by different amounts, giving a width to the ensemble. This is in contrast to homogeneous broadening, when the response of each atom is the same, as in the case of spontaneous decay.) If two-photon excitation involves absorption from two light beams with frequencies and wave vectors and , respectively, where , then the frequencies "seen" by an atom moving with velocity v are, to first order in v/c,\\
The line shape function for an atom moving with velocity v is
The Doppler effect is minimized by taking , in which case the shift is
The ensemble line shape function is obtained by averaging over the distribution of velocities. Clearly, it is desirable to use frequencies as similar as possible. The ideal case is when , which would occur in two photon-absorption from counter-propagating beams from the same laser. The simplest way to assure counter-propagating beams is to use a standing wave. Consequently, two-photon absorption in a standing wave displays no first-order Doppler broadening. Nevertheless, there is a residual second-order Doppler broadening. The second-order Doppler shift is given by
\begin{figure} \centering
\caption{Two-photon doppler-free spectrum. A narrow peak due to the process involving two photons from counterpropagating beams sits atop a broad pedestal due to that involving pairs of photons from the same beam.}
\end{figure} Taking , we have
At room temperature, eV. For hydrogen, GeV . Consequently, the fractional second order Doppler shift is about . If one considers spectroscopy at a resolution of 1 part in or better, the second order Doppler shift can be a major source of systematic error. Fortunately, methods have been developed for cooling below a millikelvin, where the effect is unimportant, at least for the next few years. Also, in heavier atoms, the second order Doppler effect is correspondingly diminished. A particularly important case is two-photon absorption on the transition in hydrogen. The 2S state is metastable and has a lifetime of 1/7 sec, yielding an extremely high Q for the transition and the possibility of ultra-high spectral resolution. The excitation operator has been calculated for hydrogen by \cite{Bassani1977}. The result yields
where the intensity is now expressed in W. A transition becomes saturated when the transition rate equals half the linewidth, or . The required power is only 0.6 W. By using two-photon Doppler-free excitation in hydrogen, H\"{a}nsch and his group have been able to achieve an experimental linewidth below 10 kHz \cite{Niering2000}. The linewidth is dominated by the time of flight of the atoms across the laser beam. Although the experimental linewidth of several kHz may seem large compared to the natural linewidth of 1 Hz, it is impressively narrow considering that the spectral linewidth was many MHz not many years ago.















![{\displaystyle a_{f}^{[1]}={\frac {1}{2i\hbar }}\int _{0}^{t}{\left[H_{fa,1}e^{-i(\omega _{1}-\omega _{fa})t^{\prime }}+H_{fa,2}e^{-i(\omega _{2}-\omega _{fa})t^{\prime }}dt^{\prime }\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a48524e887dc0de723491a5f1b013edba5a8732d)
![{\displaystyle ={\frac {1}{2\hbar }}{\left[{\frac {H_{fa,1}(e^{-i(\omega _{1}-\omega _{fa})t}-1)}{\omega _{1}-\omega _{fa}}}+{\frac {H_{fa,2}(e^{-i(\omega _{2}-\omega _{fa})t}-1)}{\omega _{2}-\omega _{fa}}}\right]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/935f78b88c94694c2a0cb19d4dde8d346f562860)

![{\displaystyle a_{b}^{[2]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/278368d4b1e3e7e1f4784fa2317a18e367883f46)
![{\displaystyle i\hbar {\dot {a}}_{b}^{[2]}=\sum _{k}H_{bk}a_{k}^{[1]}e^{i\omega _{bk}.t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01e7c88170f91f6c7bd434f2a71b568f4af3c1d5)

![{\displaystyle a_{b}^{[2]}={\frac {1}{i\hbar }}\int _{0}^{t}\langle b|H|f\rangle e^{i\omega _{bf}t^{\prime }}a_{f}^{[1]}(t^{\prime })dt^{\prime }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94d7797523cd3b2b6baeefff4f653ee5338c84a5)



![{\displaystyle {\begin{array}{rcl}a_{b}^{[2]}&=&{\frac {1}{4\hbar ^{2}}}\sum _{f}\left[{\frac {H_{bf,1}H_{fa,1}}{\omega _{1}-\omega _{fa}}}{\frac {e^{i(\omega _{0}-2\omega _{1})t}-1}{\omega _{0}-2\omega _{1}}}+{\frac {H_{bf,2}H_{fa,2}}{\omega _{2}-\omega _{fa}}}{\frac {e^{i(\omega _{0}-\omega _{2})t}-1}{\omega _{0}-2\omega _{2}}}\right.\\&&+\left.{\frac {H_{bf,2}H_{fa,1}}{\omega _{1}-\omega _{fa}}}{\frac {e^{i(\omega _{0}-\omega _{1}-\omega _{2})t}-1}{\omega _{0}-\omega _{1}-\omega _{2}}}+{\frac {H_{bf,1}H_{fa,2}}{\omega _{2}-\omega _{fa}}}{\frac {e^{i(\omega _{0}-\omega _{1}-\omega _{2})t}-1}{\omega _{0}-\omega _{1}-\omega _{2}}}\right].\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c3589d0c0f94d263f18ad021e7f291167fdf34a)


![{\displaystyle a_{b}^{[2]}\approx {\frac {1}{4\hbar ^{2}}}{\frac {H_{bk,2}H_{ka,1}}{\omega _{1}-\omega _{ka}}}{\frac {e^{i(\omega _{0}-\omega _{1}-\omega _{2})t}-1}{\omega _{1}-\omega _{1}-\omega _{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/877185fc80a5031d3a3a623fffa9a9a221113f39)
![{\displaystyle W_{a\rightarrow b}^{[2]}={\frac {1}{\left(4\hbar ^{2}\right)^{2}}}{\frac {|H_{bk,2}|^{2}|H_{ka,1}|^{2}}{(\omega _{1}-\omega _{ka})^{2}}}{\frac {\sin ^{2}\left[(\omega _{0}-\omega _{1}-\omega _{2})t/2\right]}{[(\omega _{0}-\omega _{1}-\omega _{2})/2]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf52b235d890591a2b74c238998a6c3a297877b8)
![{\displaystyle {\frac {\sin ^{2}\left[(\omega _{0}-\omega _{1}-\omega _{2})t/2\right]}{[(\omega _{0}-\omega _{1}-\omega _{2})/2]^{2}}}{\xrightarrow[{t\rightarrow \infty }]{}}2\pi t\delta (\omega _{0}-\omega _{1}-\omega _{2}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec23f6a89d79292a7a49e6172bab1c7a609c3c5d)

























![{\displaystyle \left[{\frac {\omega _{R}^{(1)}}{2\Delta }}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb3fdd79e0f3bdbd82224754ec83216ad5dbad43)


![{\displaystyle \Gamma _{ba}^{\mathrm {2-ph} }=\Gamma _{ka}\left[{\frac {H_{kb,1}}{2\Delta }}\right]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51a0a838f69cc3d14af8508753e0d9f32d5ec0c2)

![{\displaystyle \left[{\frac {H_{kb,1}}{2\Delta }}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5045eed055ce2e320e71329782faab296e3f4959)











































