Introduction
Immediately adjacent to Michelson and Morley's announcement of
their failure to find the ether in
an 1887 issue of the Philosophical Journal is a paper by the same
authors reporting that the
H line of hydrogen is actually a doublet, with a
separation of 0.33 cm
line of hydrogen is actually a doublet, with a
separation of 0.33 cm . In 1915
Bohr suggested that this "fine structure" of hydrogen is a
relativistic effect arising from the
variation of mass with velocity. Sommerfeld, in 1916, solved the
relativistic Kepler problem and
using the old quantum theory, as it was later christened, accounted
precisely for the splitting.
. In 1915
Bohr suggested that this "fine structure" of hydrogen is a
relativistic effect arising from the
variation of mass with velocity. Sommerfeld, in 1916, solved the
relativistic Kepler problem and
using the old quantum theory, as it was later christened, accounted
precisely for the splitting.
Sommerfeld's theory gave the lie to Einstein's dictum "The Good
Lord is subtle but not
malicious", for it gave the right results for the wrong reason:
his theory made no provision for
electron spin, an essential feature of fine structure. Today, all
that is left from Sommerfeld's
theory is the fine structure constant  .
The theory for the fine structure in hydrogen was provided by Dirac
whose relativistic electron theory (1926) was applied to hydrogen
by Darwin and Gordon in 1928. They found the following expression for
the energy of an electron bound to a proton of infinite mass:
.
The theory for the fine structure in hydrogen was provided by Dirac
whose relativistic electron theory (1926) was applied to hydrogen
by Darwin and Gordon in 1928. They found the following expression for
the energy of an electron bound to a proton of infinite mass:
![{\displaystyle {\frac {E}{mc^{2}}}={\left[{\frac {1}{\sqrt {\frac {\alpha Z}{n-k+{\sqrt {k^{2}-\alpha ^{2}Z^{2}}}}}}}\right]^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b03decb353205d3f96fa4b7d5d1c6a760ee73f)
where  is the principal quantum number,
is the principal quantum number,  , and
, and  .
The Dirac equation is not nearly as illuminating as the Pauli
equation, which is the approximation to the Dirac equation to the
lowest order in v/c.
.
The Dirac equation is not nearly as illuminating as the Pauli
equation, which is the approximation to the Dirac equation to the
lowest order in v/c.

The first term is the electron's rest energy; the following two
terms
are the non relativistic Hamiltonian, and the last term, the fine structure
interaction, is given by

The relativistic contributions can be described as the kinetic, spin-orbit, and Darwin terms,  ,
,  , and
, and  ,
respectively. Each has a straightforward
physical interpretation.
,
respectively. Each has a straightforward
physical interpretation.
Kinetic contribution
Relativistically, the total electron energy is E =  . The kinetic energy is
. The kinetic energy is
![{\displaystyle T=E-mc^{2}=(mc^{2}){\left[{\sqrt {1+{\frac {p^{2}}{m^{2}c^{2}}}}}-1~~\right]}={\frac {p^{2}}{2m}}-{\frac {1}{8}}{\frac {p^{4}}{m^{3}c^{2}}}+\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc695e8be75e63a5d72e966b6e14fd7eeb899702)
Thus

Spin-Orbit Interaction
According to the Dirac theory the electron has intrinsic angular
momentum  and a magnetic moment
and a magnetic moment  . The electron g-factor,
. The electron g-factor,  and the Bohr magneton
and the Bohr magneton  . As the electron
moves through the electric field of the proton it "sees" a
motional
magnetic field
. As the electron
moves through the electric field of the proton it "sees" a
motional
magnetic field

where  . However, there is
another contribution to the
effective magnetic field arising from the Thomas precession.
The relativistic transformation of a vector between two moving co-
ordinate systems which are moving with different velocities involve
not only a dilation, but also a rotation (cf Jackson,
{\it Classical Electrodynamics}).
The rate of rotation, the Thomas precession, is
. However, there is
another contribution to the
effective magnetic field arising from the Thomas precession.
The relativistic transformation of a vector between two moving co-
ordinate systems which are moving with different velocities involve
not only a dilation, but also a rotation (cf Jackson,
{\it Classical Electrodynamics}).
The rate of rotation, the Thomas precession, is

Note that the precession vanishes for co-linear acceleration.
However, for a vector fixed in a co-ordinate system moving around a
circle, as in the case of the spin vector of the electron as it
circles the proton, Thomas precession occurs. From the point of
view
of an observer fixed to the nucleus, the precession of the electron
is
identical to the effect of a magnetic field.

Substituting  , and
, and  into Eq.\ \ref{EQ_soitwo} gives
into Eq.\ \ref{EQ_soitwo} gives

Hence the total effective magnetic field is

This gives rise to a total spin-orbit interaction

The Darwin Term
Electrons exhibit "Zitterbewegung", fluctuations in position on
the order of the Compton
wavelength,  . As a result, the effective Coulombic
potential is not
. As a result, the effective Coulombic
potential is not  , but some
suitable average
, but some
suitable average  , where the average is
over the characteristic
distance
, where the average is
over the characteristic
distance  . To evaluate this, expand
. To evaluate this, expand  about
about
 in terms of a
displacement
in terms of a
displacement  ,
,

Assume that the fluctuations are isotropic. Then the time average
of
 is
is
![{\displaystyle \Delta V\sim {\frac {1}{2}}{\left[{\frac {1}{3}}{\left({\frac {\hbar }{mc}}\right)^{2}}\right]}\nabla ^{2}V=-{\frac {1}{6}}{\frac {e^{2}\hbar ^{2}}{m^{2}c^{2}}}\nabla ^{2}\left({\frac {1}{r}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90dd5f34606adfcb4dbc1b8d5ca7df80561feedb)
The precise expression for the Darwin term is

The coefficient of the Darwin term is 1/8, rather than 1/6.
Recall that  , so that the Darwin term is nonzero only for
, so that the Darwin term is nonzero only for  states, where
states, where  .
That is, the Zitterbewegung effectively cuts off the cusp of the
.
That is, the Zitterbewegung effectively cuts off the cusp of the  potential, thereby reducing the binding energy for
potential, thereby reducing the binding energy for  -electrons.
-electrons.
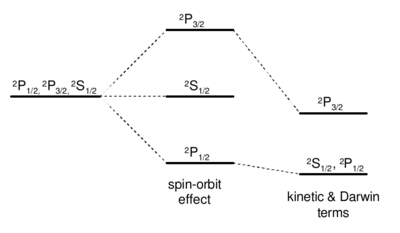
Evaluation of the fine structure interaction
Fine structure of  levels in hydrogen. The degeneracy between the
levels in hydrogen. The degeneracy between the  and
and  levels, which looks accidental in non-relativistic quantum mechanics, is really deeply rooted in the relativistic nature of the system. The degeneracy is ultimatly broken in QED by the Lamb Shift.
levels, which looks accidental in non-relativistic quantum mechanics, is really deeply rooted in the relativistic nature of the system. The degeneracy is ultimatly broken in QED by the Lamb Shift.
The spin orbit-interaction is not diagonal in  or {\bf
S} due to the term
or {\bf
S} due to the term  . However, it is diagonal
in
. However, it is diagonal
in
 .
.  and
and  are likewise
diagonal in
are likewise
diagonal in  . Hence, finding the energy level structure
due
to the fine structure interaction involves evaluating
. Hence, finding the energy level structure
due
to the fine structure interaction involves evaluating
 .
Note that
.
Note that  vanishes in an
vanishes in an  state, and that
state, and that
 vanishes in all states but an
vanishes in all states but an  state. It is left as an
exercise to show that
state. It is left as an
exercise to show that

Note that states of a given  and
and  are degenerate. This
degeneracy
is a crucial feature of the Dirac theory.
are degenerate. This
degeneracy
is a crucial feature of the Dirac theory.
The Lamb Shift
According to the Dirac theory, states of the hydrogen atom with the
same values of  and
and  are degenerate. Hence, in a given term,
(
are degenerate. Hence, in a given term,
( ), (
), ( ), (
), ( ), etc. form degenerate
doublets. However, as described in Chapter 1, this is not exactly
the
case. Because of vacuum interactions, not taken into account, in
the
Dirac theory, the degeneracy is broken. The largest effect is in
the
), etc. form degenerate
doublets. However, as described in Chapter 1, this is not exactly
the
case. Because of vacuum interactions, not taken into account, in
the
Dirac theory, the degeneracy is broken. The largest effect is in
the
 state. The energy splitting between the
state. The energy splitting between the  and
and
 states is called the Lamb Shift. A
simple physical model due to Welton and Weisskopf demonstrate its
origin. In the following derivation, note the analogy between the vacuum
fluctuations inducing the Lamb Shift and the Zitterbewegung responsible for the
Darwin term treated in section \ref{SEC_dt}.
Because of zero point fluctuation in the vacuum, empty space is not
truly empty. The electromagnetic modes of free space behave like
harmonic oscillators, each with zero-point energy
states is called the Lamb Shift. A
simple physical model due to Welton and Weisskopf demonstrate its
origin. In the following derivation, note the analogy between the vacuum
fluctuations inducing the Lamb Shift and the Zitterbewegung responsible for the
Darwin term treated in section \ref{SEC_dt}.
Because of zero point fluctuation in the vacuum, empty space is not
truly empty. The electromagnetic modes of free space behave like
harmonic oscillators, each with zero-point energy  . The
density of modes per unit frequency interval and per volume is
given
by the well known expression
. The
density of modes per unit frequency interval and per volume is
given
by the well known expression

Consequently, the zero-point energy density is

With this energy we can associate a spectral density of radiation

The bar denotes a time average and  and
and  are the
field amplitudes. Hence,
are the
field amplitudes. Hence,

For the moment we shall treat the electron as if it were free. Its
motion is given by


The effect of the fluctuation  is to cause a change
is to cause a change
 in the average potential
in the average potential

 can be found by a Taylor's expansion:
can be found by a Taylor's expansion:

When we average this in time, the second term vanishes because {\bf
s} averages to zero. For the
same reason, in the final term, only contributions with  remain. We have, taking the average,
remain. We have, taking the average,

Since  we
obtain finally
we
obtain finally

Since  , we
obtain
the following expression for the change in energy
, we
obtain
the following expression for the change in energy

The matrix element gives contributions only for  states, where
its
value is
states, where
its
value is

Combining Eqs.\ \ref{EQ_lambsix}, \ref{EQ_lambtweleve} into Eq.\
\ref{EQ_lambeleven} yields

Integrating over some yet to be specified frequency limits, we
obtain

At this point, atomic units come in handy. Converting by the usual
prescription, we obtain

The question remaining is how to choose the cut-off frequencies for
the integration. It is reasonable that  is
approximately
the frequency of an orbiting electron,
is
approximately
the frequency of an orbiting electron,  in atomic
units. At lower energies, the electron could not respond. For the
upper limit, a plausible guess is the rest energy of the electron,
in atomic
units. At lower energies, the electron could not respond. For the
upper limit, a plausible guess is the rest energy of the electron,
 . Hence,
. Hence,  .
For the
.
For the  state, this gives
state, this gives
 atomic~units
atomic~units  MHz
MHz
The actual value is 1,058 MHz.
Measurements of the Lamb shift \cite{Lamb1947, Weitz1994, Schwob1999} have occupied the forefront of hydrogen spectroscopy from Lamb's original 1947 discovery, using microwave techniques, of a shift of "about 1000 Mc/sec" to more recent results at the  level of precision obtained in the optical domain by two-photon spectroscopy.
level of precision obtained in the optical domain by two-photon spectroscopy.
Notes



![{\displaystyle {\frac {E}{mc^{2}}}={\left[{\frac {1}{\sqrt {\frac {\alpha Z}{n-k+{\sqrt {k^{2}-\alpha ^{2}Z^{2}}}}}}}\right]^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b03decb353205d3f96fa4b7d5d1c6a760ee73f)









![{\displaystyle T=E-mc^{2}=(mc^{2}){\left[{\sqrt {1+{\frac {p^{2}}{m^{2}c^{2}}}}}-1~~\right]}={\frac {p^{2}}{2m}}-{\frac {1}{8}}{\frac {p^{4}}{m^{3}c^{2}}}+\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc695e8be75e63a5d72e966b6e14fd7eeb899702)





















![{\displaystyle \Delta V\sim {\frac {1}{2}}{\left[{\frac {1}{3}}{\left({\frac {\hbar }{mc}}\right)^{2}}\right]}\nabla ^{2}V=-{\frac {1}{6}}{\frac {e^{2}\hbar ^{2}}{m^{2}c^{2}}}\nabla ^{2}\left({\frac {1}{r}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90dd5f34606adfcb4dbc1b8d5ca7df80561feedb)