The master equation is an equation of motion for a density
matrix describing an open quantum system, much like the Schrodinger
equation describes the evolution of a closed quantum system. This
section provides a derivation of the master equation for a
spontaneously emitting atom, driven by a classical field, which is
known as the Optical Bloch Equation.
Classical model of atom and field
A good starting point, to appreciate the problem of open quantum
systems, is the classical model for a two-level atom coupled to a
black-body electromagnetic field, the Einstein rate equations
![{\displaystyle {\begin{array}{rcl}{\frac {dN_{g}}{dt}}&=&A_{eg}N_{e}+u(\omega _{eg})\left[{B_{eg}N_{e}-B_{ge}N_{g}}\right]\\{\frac {dN_{e}}{dt}}&=&-A_{eg}N_{e}+u(\omega _{eg})\left[{B_{ge}N_{g}-B_{eg}N_{e}}\right]\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3de5ce121e7274142196ed5bff99e7d150536dba)
where  is the spontaneous emission rate,
is the spontaneous emission rate,  and
and  are stimulated emission rates, and
are stimulated emission rates, and  is the field
energy density at atomic frequency
is the field
energy density at atomic frequency  , for levels denoted
by
, for levels denoted
by  and
and  .
.
Is there a straightforward quantum analogue of this? We might be
tempted to simply add a damping term to the Schrödinger equation,
like

but this is not physically allowed by quantum mechanics!
How, then, can we construct a fully quantum-mechanical description of
open system dynamics? The key concept is that we must properly
account for noise:
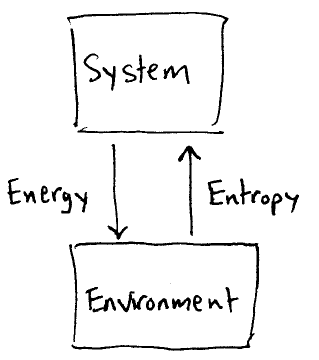
From classical thermodynamics, we know that any time there is energy
transfer from a system to the environment, there is entropy exchanged
back from the environment to the system. This is a simple
illustration of the very basic fluctuation--dissipation
principle: there can be no relaxation without con-commitment noise!
To study quantum open system, we must model the appropriate quantum
noise contribution which goes along with relaxation.
Density matrices and closed system dynamics
The main tool we shall use to model open quantum systems is the
density matrix representation for quantum states, so it is helpful to
begin with a review of density matrices and how they evolve under
Hamiltonian dynamics.
Review of density matrices: definition, properties, and unravlings
Recall that a density matrix  for a pure state
for a pure state  is the
matrix
is the
matrix  . Thus, for example
. Thus, for example
![{\displaystyle {\begin{array}{rcl}|0\rangle &\rightarrow &\left[{\begin{array}{cc}{1}&{0}\\{0}&{0}\end{array}}\right]\\&&~\\|1\rangle &\rightarrow &\left[{\begin{array}{cc}{0}&{0}\\{0}&{1}\end{array}}\right]\\&&~\\{\frac {|0{\rangle }+|1{\rangle }}{\sqrt {2}}}&\rightarrow &{\frac {1}{2}}\left[{\begin{array}{cc}{1}&{1}\\{1}&{1}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/148a72103d1f8644a8ff701d4867962d1d159cdf)
Density matrices may also represent statistical mixtures of pure
states; this state
![{\displaystyle {\frac {1}{2}}\left[{\begin{array}{cc}{1}&{0}\\{0}&{1}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1419b7570ed9a93e84cf5f1c5dde4a289caaf121)
can be interpreted as a 50/50 mixture of  and
and  . However,
one must be careful, because there are infinitely many ways to unravel a density matrix into statistical mixtures of pure states.
. However,
one must be careful, because there are infinitely many ways to unravel a density matrix into statistical mixtures of pure states.
For example,
![{\displaystyle \rho ={\frac {1}{4}}\left[{\begin{array}{cc}{3}&{0}\\{0}&{1}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb97d483bbe12ab29a91dc26b6d75454b16d5101)
is

but it is also

where

In general, a density matrix  may always be written as a
statistical mixture of pure states,
may always be written as a
statistical mixture of pure states,

where  are probabilities, such that
are probabilities, such that  .
.
A matrix  is a valid density matrix if and only if the
eigenvalues of
is a valid density matrix if and only if the
eigenvalues of  are non-negative, and sum to one, such that
are non-negative, and sum to one, such that
 .
.  represents a pure state if and only if
represents a pure state if and only if
 .
.
Density matrices: closed system evolution
How does a density matrix evolve in a closed system? From the
Schrodinger equation

it follows that a pure state
density matrix  evolves as
evolves as
![{\displaystyle {\begin{array}{rcl}{\dot {\rho }}&=&|{\dot {\psi }}{\rangle }{\langle }\psi |+|\psi {\rangle }{\langle }{\dot {\psi }}|\\&=&-{\frac {i}{\hbar }}[H,\rho ]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ef8a3f7741d64ed346a826af5898616aa94f1ff)
For example, if  is a two-level atom evolving under the
classical field Jaynes-Cummings Hamiltonian
is a two-level atom evolving under the
classical field Jaynes-Cummings Hamiltonian

which we may express using Pauli matrices as

then for
![{\displaystyle \rho =\left[{\begin{array}{cc}{\rho _{ee}}&{\rho _{eg}}\\{\rho _{ge}}&{\rho _{gg}}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/614be7a08a95774b74f988c678248fd3055558a9)
the equation of motion for  is
is
![{\displaystyle {\dot {\rho }}=\left[{\begin{array}{cc}{i\Omega (\rho _{eg}-\rho _{ge})}&{i\omega _{0}\rho _{ge}-i\Omega (\rho _{ee}-\rho _{gg})}\\{-i\omega _{0}\rho _{eg}+i\Omega (\rho _{ee}-\rho _{gg})}&{i\Omega (\rho _{eg}-\rho _{ge})}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3cfc983a937ff205c0e587cfadbabf2e5ead5bd)
We can recognize this as a rotation of the Bloch sphere about the axis
defined by

by using the Bloch sphere representation for a density matrix,

Density matrices and open system dynamics: approach
We can build a mathematical model for quantum open system dynamics,
based on four basic ideas:
|
Density matrix evolution
|
Instead of pure states (eg  ), we describe the system
state using a density matrix ), we describe the system
state using a density matrix  . The equation of motion
for . The equation of motion
for  is is
![{\displaystyle {\dot {\rho }}={\mathcal {L}}[\rho ]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87df51b305d27ed4c8d618237dca2d1afb66637d)
where  is known as the Liouvillian operator (or a
"superoperator"). For example, for Hamiltonian evolution,
we have: is known as the Liouvillian operator (or a
"superoperator"). For example, for Hamiltonian evolution,
we have:

which, for  gives gives
![{\displaystyle {\begin{array}{rcl}\partial _{t}\rho &=&|{\dot {\psi }}{\rangle }{\langle }\psi |+|\psi {\rangle }{\langle }{\dot {\psi }}|\\&=&-{\frac {i}{\hbar }}H|\psi {\rangle }{\langle }\psi |+|\psi {\rangle }{\langle }\psi |{\frac {i}{\hbar }}H\\&=&-{\frac {i}{\hbar }}[H,\rho ]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55e043164c576ee542972da45eb3efb361fbcf98)
This is unitary evolution, but in general, the differential
equation for  can describe non-unitary evolution.
Such differential equations are known as "master equations."
They are nontrivial to construct, because they must restrict can describe non-unitary evolution.
Such differential equations are known as "master equations."
They are nontrivial to construct, because they must restrict
 to be a legitimate density matrix at all times. to be a legitimate density matrix at all times.
|
|
Partial trace
|
We are interested in the state of the system alone, and want
to disregard the state of the environment. If  is the state of the whole system + environment, then
the state of the system alone is is the state of the whole system + environment, then
the state of the system alone is
![{\displaystyle {\begin{array}{rcl}\rho _{sys}&=&{\rm {Tr}}_{env}\left[{\rho _{\rm {total}}}\right]\\&=&\sum _{\rm {env}}{\langle }{\rm {env}}|\rho _{\rm {total}}|{\rm {env}}{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f323682e581f606a2b4f9be4d38f808f5a533ce8)
|
|
Assumptions about the environment
|
The environment is also known as a "bath" or a "reservoir"
(cf API). We model it as being an ensemble of oscillators, of
a variety of frequencies, which are weakly coupled to the
system. It has several important properties:
- Large and unchanging -- Born approximation
- Short correlation time
 -- Markov approximation -- Markov approximation
|
|
Two (very different) timescales
|
There are two important timescales in this model:
 : A slow evolution of the system : A slow evolution of the system : The fast fluctuations of the environment : The fast fluctuations of the environment
We will build equations of motion which have a timescale
 , chosen such that , chosen such that  . .
|
Our goal is to construct a model dynamical equation of motion for
 of the form
of the form

where  is time independent. This is known as a "coarse grained"
evolution equation. It is desirable to obtain
is time independent. This is known as a "coarse grained"
evolution equation. It is desirable to obtain  for a variety of
scenarios, including interactions where the system + environment are
atom + light, light + light, and atom + motion, for example. Below,
we construct a master equation for the atom + vacuum using two
different approaches.
for a variety of
scenarios, including interactions where the system + environment are
atom + light, light + light, and atom + motion, for example. Below,
we construct a master equation for the atom + vacuum using two
different approaches.
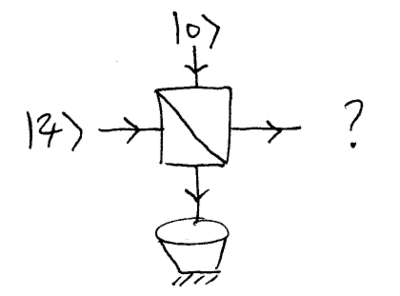
Beamsplitter model of the master equation
The physical intuition behind the master equation we desire to
construct can be captured with a simple example, which builds on the
beamsplitter we studied in previous lectures. Consider a single
photon state  (for simplicity, let the
coefficients be real-valued) entering a beamsplitter of angle
(for simplicity, let the
coefficients be real-valued) entering a beamsplitter of angle
 :
:
A vacuum state  is input to the other port, whose output we
discard. Let us consider the photon as being our system, and the
other (initially vacuum) mode as being our environment. What is the
quantum state of the undiscarded output? Naively, we might argue that
a single photon is discarded into the environment with probability
is input to the other port, whose output we
discard. Let us consider the photon as being our system, and the
other (initially vacuum) mode as being our environment. What is the
quantum state of the undiscarded output? Naively, we might argue that
a single photon is discarded into the environment with probability
 , so that we might expect the output to be
, so that we might expect the output to be
 with probability
with probability  , and
, and  with probability
with probability  .
.
However, that (semi-)classical argument is incorrect.
The output state  of the system + environment is
of the system + environment is
![{\displaystyle {\begin{array}{rcl}|\phi \rangle &=&e^{i\theta (a^{\dagger }b+b^{\dagger }a)}\left[{|\psi \rangle \otimes |0\rangle }\right]\\&=&\alpha |00\rangle +\beta \left[{\cos \theta |10\rangle +\sin \theta |01\rangle }\right]\\&=&\left[{\alpha |0\rangle +\beta \cos \theta |1\rangle }\right]\otimes |0{\rangle }+\left[{\beta \sin \theta |0\rangle }\right]\otimes |1{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60b46fb8e3f4ea4009cb0caf23b5a3ef491b1c4)
Thus, the correct result is that the output is  , with
probability
, with
probability  , and
, and  with probability
with probability  .
.
These states can conveniently be written as density matrices. The
input state is
![{\displaystyle \rho _{in}=|\psi {\rangle }{\langle }\psi |=\left[{\begin{array}{cc}{\alpha ^{2}}&{\alpha \beta }\\{\alpha \beta }&{\beta ^{2}}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/665d8422dd6da868f3dac0c6b267a669c62ad1e2)
and the output state is
![{\displaystyle {\begin{array}{rcl}\rho _{out}=p_{1}|\psi _{1}{\rangle }{\langle }\psi _{1}|+p_{0}|\psi _{0}{\rangle }{\langle }\psi _{0}|=\left[{\begin{array}{cc}{\alpha ^{2}+\beta ^{2}\sin ^{2}\theta }&{\alpha \beta \cos \theta }\\{\alpha \beta \cos \theta }&{\beta ^{2}\cos ^{2}\theta }\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17813b3a8608cb01b63bfca36257facdb37766d)
Note that  cannot be written as
cannot be written as  for any
pure state
for any
pure state  , because it is not pure (it is a statistical mixture).
The change in
, because it is not pure (it is a statistical mixture).
The change in  is
is
![{\displaystyle \Delta \rho =\rho _{out}-\rho _{in}=\left[{\begin{array}{cc}{-\beta ^{2}(\cos 2\theta -1)/2}&{\alpha \beta (\cos \theta -1)}\\{\alpha \beta (\cos \theta -1)}&{\beta ^{2}(\cos 2\theta -1)/2}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ad1199214dd390699b05de3872d4e24703ebe0)
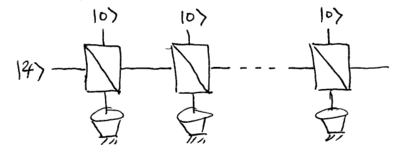
Now imagine that we send the single photon state through many
beamsplitters in a sequence, each with some small tap angle  :
:
We make two assumptions: the environment modes always begin in the
vacuum  (this is the Born approximation), and the environment is
completely different and uncorrelated between scattering events (this
is the Markov approximation).
(this is the Born approximation), and the environment is
completely different and uncorrelated between scattering events (this
is the Markov approximation).
This allows us to write a coarse-grained differential equation for the
photon state
![{\displaystyle {\frac {\Delta \rho }{\Delta t}}\approx \left[{\begin{array}{cc}{{\dot {\rho }}_{00}}&{{\dot {\rho }}_{01}}\\{{\dot {\rho }}_{10}}&{{\dot {\rho }}_{11}}\end{array}}\right]=-\Gamma \left[{\begin{array}{cc}{-\beta ^{2}}&{\alpha \beta /2}\\{\alpha \beta /2}&{\beta ^{2}}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b85bb3e25977fa72beb51f8f1aa3d5a42bf92377)
Expressed as differential equations for each of the independent matrix
elements, we get (using Eq.(\ref{eq:rhoin}) for  )
)

for the diagonal elements. These describe the evolutions of the
probabilities of finding the photon in the  and
and  states,
and are analogous to the Einstein rate equations. And for the
off-diagonal elements we get
states,
and are analogous to the Einstein rate equations. And for the
off-diagonal elements we get

which show the decay of the quantum coherence of the state.
The form of these differential equations, which are master equations,
is very general, and almost exactly the same result is obtained for a
two-level atom interacting with the vacuum. In that situation, the
solution differs essentially only in that the coherences evolve as

where  is a frequency shift of the system known as the "Lamb
shift," which is due to virtual excitations to higher atomic levels.
is a frequency shift of the system known as the "Lamb
shift," which is due to virtual excitations to higher atomic levels.
In the atomic master equation,  is the spontaneous emission
rate, given by Fermi's golden rule
is the spontaneous emission
rate, given by Fermi's golden rule

as derived elsewhere.
Full derivation -- walk-through
We now turn to a full derivation of the general master equation.
Following the notation used in API, Chapter 4, let  denote the
system, and
denote the
system, and  the environment (known as the reservoir in API). The
full Hamiltonian is
the environment (known as the reservoir in API). The
full Hamiltonian is

where  is the system-reservoir interaction potential. In the
interaction picture defined by
is the system-reservoir interaction potential. In the
interaction picture defined by  and
and  , the equation of motion
for the full system + reservoir density matrix is
, the equation of motion
for the full system + reservoir density matrix is
![{\displaystyle i\hbar {\dot {\rho }}=[V,\rho ]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6eee125f007a6997757c5f6f414236e7e6110953)
Integrating this once gives
![{\displaystyle i\hbar \rho (t)=\int _{0}^{t}[V(t'),\rho (t')]\,dt'\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffa8f401d6fe2ebea8c927123978036a86394118)
Substituting this back into Eq.(\ref{eq:vnrho}) gives
![{\displaystyle {\dot {\rho }}=-{\frac {1}{\hbar ^{2}}}\int _{0}^{t}[V(t),[V(t'),\rho (t')]]\,dt'\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e0f8e184b43e75a6e00f2fd56e57749607cd358)
If we assume that the system and reservoir are initially uncorrelated,
and make the approximation that the reservoir stays unchanged (the
Born approximation), then

This gives us our starting point for a general master equation:
![{\displaystyle {\dot {\rho }}_{A}=-{\frac {1}{\hbar ^{2}}}{\rm {Tr}}_{R}\int _{0}^{t}[V(t),[V(t'),\rho _{A}(t')\otimes \rho _{R}]]\,dt'\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/952e07f5b5b861e6a4e887350e415d0fa35d87f1)
An example is helpful in seeing how this equation works. Generally,
we will take system + reservoir interactions of the form  ,
where
,
where  acts only on the system, and
acts only on the system, and  acts only on the
reservoir. Specifically, let the system be a two-level atom, and the
environment be a single electromagnetic mode initially in the vacuum
state
acts only on the
reservoir. Specifically, let the system be a two-level atom, and the
environment be a single electromagnetic mode initially in the vacuum
state  . The atom interacts with the usual dipole interaction,
. The atom interacts with the usual dipole interaction,

which is conveniently written using Pauli raising and lowering
operators

where

Insert this now into Eq.(\ref{eq:rhome}), but disregard the integral
over time (this lets us see what the essential dynamics are, at the
expense of not obtaining the correct specific rates). The
relevant commutators are
![{\displaystyle \left[{V,\rho _{A}\otimes |0\rangle \langle 0|}\right]=(\sigma _{-}\rho _{A})\otimes |1\rangle \langle 0|-(\rho _{A}\sigma _{+})\otimes |0\rangle \langle 1|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e71f8dcb754e18262c8e0a348808d4fc6e2d581)
and
![{\displaystyle \left[{V,\left[{V,\rho _{A}\otimes |0\rangle \langle 0|}\right]}\right]=(\sigma _{+}\sigma _{-}\rho _{A})\otimes |0\rangle \langle 0|-2(\sigma _{-}\rho _{A}\sigma _{+})\otimes |1\rangle \langle 1|+(\rho _{A}\sigma _{+}\sigma _{-})|0\rangle \langle 0|+{\rm {other}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b483417e28676f357122e1171d551cbb0106443)
where the "other" terms are not diagonal in the electromagnetic mode
states, and thus disappear in the partial trace over the reservoir.
We find, finally:
![{\displaystyle {\dot {\rho }}_{A}=-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho _{A}-2\sigma _{-}\rho _{A}\sigma _{+}+\rho _{A}\sigma _{+}\sigma _{-}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/566d9fe7364eda8cb046cf6bf5e01c356ba9b845)
This is the master equation for a two-level atom dipole coupled to a
single electromagnetic mode initially in the vacuum state. It is
written in a form known as the "Lindblad" form, which is very
common. In atomic physics, you will often see master equations like
this. The Lindblad form has the special property that it ensures
 is a legitimate density matrix at all times; not only does
is a legitimate density matrix at all times; not only does
 always, but also, its eigenvalues remain
non-negative. And more importantly, the map from
always, but also, its eigenvalues remain
non-negative. And more importantly, the map from  to
to
 is completely positive, meaning that if the map
operates on just part of a larger system, the state of the larger
system remains described by a valid, positive density matrix.
Using the definitions for
is completely positive, meaning that if the map
operates on just part of a larger system, the state of the larger
system remains described by a valid, positive density matrix.
Using the definitions for  , if we express
, if we express  as
as
![{\displaystyle \rho _{A}=\left[{\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcda3168aa585bf956d6af991a40bc31d894b9e6)
then we find
![{\displaystyle {\dot {\rho }}_{A}=-\Gamma \left[{\begin{array}{cc}{2a}&{b}\\{c}&{-2a}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c40693f462306f71b3583d205fa0e5714a063f8)
which is identical to the master equation we constructed for the
beamsplitter example, Eq.(\ref{eq:bsme}), up to a relabeling of  and
and  .
As shown by this example, the physical picture behind the master
equation is not so complicated, even though the mathematics (used in
all its glory) can be overwhelming.
The equation of motion for
.
As shown by this example, the physical picture behind the master
equation is not so complicated, even though the mathematics (used in
all its glory) can be overwhelming.
The equation of motion for  we have obtained is very close
to the classical Einstein equations we began with, as we can see by
writing out equations of motion for the individual components of
we have obtained is very close
to the classical Einstein equations we began with, as we can see by
writing out equations of motion for the individual components of
 . Explicitly, and including Hamiltonian evolution under the
classical field Jaynes-Cummings interaction, we find
. Explicitly, and including Hamiltonian evolution under the
classical field Jaynes-Cummings interaction, we find

where the other two components are given by  and
and
 . These differential equations are known as
the Optical Bloch Equations, and we will base a great deal of
our study of atoms and light forces on this quantum description of
open system dynamics of a spontaneously emitting atom driven by a
classical field.
. These differential equations are known as
the Optical Bloch Equations, and we will base a great deal of
our study of atoms and light forces on this quantum description of
open system dynamics of a spontaneously emitting atom driven by a
classical field.
References
![{\displaystyle {\begin{array}{rcl}{\frac {dN_{g}}{dt}}&=&A_{eg}N_{e}+u(\omega _{eg})\left[{B_{eg}N_{e}-B_{ge}N_{g}}\right]\\{\frac {dN_{e}}{dt}}&=&-A_{eg}N_{e}+u(\omega _{eg})\left[{B_{ge}N_{g}-B_{eg}N_{e}}\right]\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3de5ce121e7274142196ed5bff99e7d150536dba)











![{\displaystyle {\begin{array}{rcl}|0\rangle &\rightarrow &\left[{\begin{array}{cc}{1}&{0}\\{0}&{0}\end{array}}\right]\\&&~\\|1\rangle &\rightarrow &\left[{\begin{array}{cc}{0}&{0}\\{0}&{1}\end{array}}\right]\\&&~\\{\frac {|0{\rangle }+|1{\rangle }}{\sqrt {2}}}&\rightarrow &{\frac {1}{2}}\left[{\begin{array}{cc}{1}&{1}\\{1}&{1}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/148a72103d1f8644a8ff701d4867962d1d159cdf)
![{\displaystyle {\frac {1}{2}}\left[{\begin{array}{cc}{1}&{0}\\{0}&{1}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1419b7570ed9a93e84cf5f1c5dde4a289caaf121)


![{\displaystyle \rho ={\frac {1}{4}}\left[{\begin{array}{cc}{3}&{0}\\{0}&{1}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb97d483bbe12ab29a91dc26b6d75454b16d5101)










![{\displaystyle {\begin{array}{rcl}{\dot {\rho }}&=&|{\dot {\psi }}{\rangle }{\langle }\psi |+|\psi {\rangle }{\langle }{\dot {\psi }}|\\&=&-{\frac {i}{\hbar }}[H,\rho ]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ef8a3f7741d64ed346a826af5898616aa94f1ff)


![{\displaystyle \rho =\left[{\begin{array}{cc}{\rho _{ee}}&{\rho _{eg}}\\{\rho _{ge}}&{\rho _{gg}}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/614be7a08a95774b74f988c678248fd3055558a9)
![{\displaystyle {\dot {\rho }}=\left[{\begin{array}{cc}{i\Omega (\rho _{eg}-\rho _{ge})}&{i\omega _{0}\rho _{ge}-i\Omega (\rho _{ee}-\rho _{gg})}\\{-i\omega _{0}\rho _{eg}+i\Omega (\rho _{ee}-\rho _{gg})}&{i\Omega (\rho _{eg}-\rho _{ge})}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3cfc983a937ff205c0e587cfadbabf2e5ead5bd)


![{\displaystyle {\dot {\rho }}={\mathcal {L}}[\rho ]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87df51b305d27ed4c8d618237dca2d1afb66637d)


![{\displaystyle {\begin{array}{rcl}\partial _{t}\rho &=&|{\dot {\psi }}{\rangle }{\langle }\psi |+|\psi {\rangle }{\langle }{\dot {\psi }}|\\&=&-{\frac {i}{\hbar }}H|\psi {\rangle }{\langle }\psi |+|\psi {\rangle }{\langle }\psi |{\frac {i}{\hbar }}H\\&=&-{\frac {i}{\hbar }}[H,\rho ]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55e043164c576ee542972da45eb3efb361fbcf98)

![{\displaystyle {\begin{array}{rcl}\rho _{sys}&=&{\rm {Tr}}_{env}\left[{\rho _{\rm {total}}}\right]\\&=&\sum _{\rm {env}}{\langle }{\rm {env}}|\rho _{\rm {total}}|{\rm {env}}{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f323682e581f606a2b4f9be4d38f808f5a533ce8)













![{\displaystyle {\begin{array}{rcl}|\phi \rangle &=&e^{i\theta (a^{\dagger }b+b^{\dagger }a)}\left[{|\psi \rangle \otimes |0\rangle }\right]\\&=&\alpha |00\rangle +\beta \left[{\cos \theta |10\rangle +\sin \theta |01\rangle }\right]\\&=&\left[{\alpha |0\rangle +\beta \cos \theta |1\rangle }\right]\otimes |0{\rangle }+\left[{\beta \sin \theta |0\rangle }\right]\otimes |1{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60b46fb8e3f4ea4009cb0caf23b5a3ef491b1c4)


![{\displaystyle \rho _{in}=|\psi {\rangle }{\langle }\psi |=\left[{\begin{array}{cc}{\alpha ^{2}}&{\alpha \beta }\\{\alpha \beta }&{\beta ^{2}}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/665d8422dd6da868f3dac0c6b267a669c62ad1e2)
![{\displaystyle {\begin{array}{rcl}\rho _{out}=p_{1}|\psi _{1}{\rangle }{\langle }\psi _{1}|+p_{0}|\psi _{0}{\rangle }{\langle }\psi _{0}|=\left[{\begin{array}{cc}{\alpha ^{2}+\beta ^{2}\sin ^{2}\theta }&{\alpha \beta \cos \theta }\\{\alpha \beta \cos \theta }&{\beta ^{2}\cos ^{2}\theta }\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17813b3a8608cb01b63bfca36257facdb37766d)



![{\displaystyle \Delta \rho =\rho _{out}-\rho _{in}=\left[{\begin{array}{cc}{-\beta ^{2}(\cos 2\theta -1)/2}&{\alpha \beta (\cos \theta -1)}\\{\alpha \beta (\cos \theta -1)}&{\beta ^{2}(\cos 2\theta -1)/2}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ad1199214dd390699b05de3872d4e24703ebe0)

![{\displaystyle {\frac {\Delta \rho }{\Delta t}}\approx \left[{\begin{array}{cc}{{\dot {\rho }}_{00}}&{{\dot {\rho }}_{01}}\\{{\dot {\rho }}_{10}}&{{\dot {\rho }}_{11}}\end{array}}\right]=-\Gamma \left[{\begin{array}{cc}{-\beta ^{2}}&{\alpha \beta /2}\\{\alpha \beta /2}&{\beta ^{2}}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b85bb3e25977fa72beb51f8f1aa3d5a42bf92377)













![{\displaystyle i\hbar {\dot {\rho }}=[V,\rho ]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6eee125f007a6997757c5f6f414236e7e6110953)
![{\displaystyle i\hbar \rho (t)=\int _{0}^{t}[V(t'),\rho (t')]\,dt'\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffa8f401d6fe2ebea8c927123978036a86394118)
![{\displaystyle {\dot {\rho }}=-{\frac {1}{\hbar ^{2}}}\int _{0}^{t}[V(t),[V(t'),\rho (t')]]\,dt'\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e0f8e184b43e75a6e00f2fd56e57749607cd358)

![{\displaystyle {\dot {\rho }}_{A}=-{\frac {1}{\hbar ^{2}}}{\rm {Tr}}_{R}\int _{0}^{t}[V(t),[V(t'),\rho _{A}(t')\otimes \rho _{R}]]\,dt'\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/952e07f5b5b861e6a4e887350e415d0fa35d87f1)




![{\displaystyle \left[{V,\rho _{A}\otimes |0\rangle \langle 0|}\right]=(\sigma _{-}\rho _{A})\otimes |1\rangle \langle 0|-(\rho _{A}\sigma _{+})\otimes |0\rangle \langle 1|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e71f8dcb754e18262c8e0a348808d4fc6e2d581)
![{\displaystyle \left[{V,\left[{V,\rho _{A}\otimes |0\rangle \langle 0|}\right]}\right]=(\sigma _{+}\sigma _{-}\rho _{A})\otimes |0\rangle \langle 0|-2(\sigma _{-}\rho _{A}\sigma _{+})\otimes |1\rangle \langle 1|+(\rho _{A}\sigma _{+}\sigma _{-})|0\rangle \langle 0|+{\rm {other}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b483417e28676f357122e1171d551cbb0106443)
![{\displaystyle {\dot {\rho }}_{A}=-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho _{A}-2\sigma _{-}\rho _{A}\sigma _{+}+\rho _{A}\sigma _{+}\sigma _{-}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/566d9fe7364eda8cb046cf6bf5e01c356ba9b845)




![{\displaystyle \rho _{A}=\left[{\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcda3168aa585bf956d6af991a40bc31d894b9e6)
![{\displaystyle {\dot {\rho }}_{A}=-\Gamma \left[{\begin{array}{cc}{2a}&{b}\\{c}&{-2a}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c40693f462306f71b3583d205fa0e5714a063f8)



