Resonances
Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\unit{}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\hertz{{\rm Hz}}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\kelvin{{\rm K}}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\metre{{\rm m}}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\reciprocal[1]{{#1}^{-1}}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\mega{{\rm M}}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\micro{\mu}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\kilo{{\rm k}}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\second{{\rm s}}} Failed to parse (unknown function "\newcommand"): {\displaystyle \newcommand\per{/}}
Contents
- 1 Classical Resonances
- 2 Magnetic Resonance: The Classical Magnetic Moment in a Spatially Uniform Field
- 2.1 Harmonic oscillator versus two-level systems
- 2.2 Magnetic Moment in a Static Field
- 2.3 Transformation to a Rotating Coordinate System
- 2.4 Larmor's Theorem for a Charged Particle in a Magnetic Field
- 2.5 Rotating Magnetic Field on Resonance
- 2.6 Rotating Magnetic Field Off-Resonance
- 2.7 "Rapid" Adiabiatic Passage (Classical Treatment)
- 3 Quantized Spin in a Magnetic Field
- 3.1 Equation of Motion for the Expectation Value
- 3.2 The Two-Level System: Spin-1/2
- 3.3 Matrix form of Hamiltonian
- 3.4 Solution of the Schrodinger Equation for Spin-1/2 in the Rotating Frame
- 3.5 Solution of the Schrodinger Equation for Spin-1/2 in the Interaction Representation
- 3.6 "Rapid" Adiabiatic Passage (Quantum Treatment)
- 4 Decoherence Processes, Mixed States, Density Matrices
- 5 References
- 6 Notes
Classical Resonances
Introduction
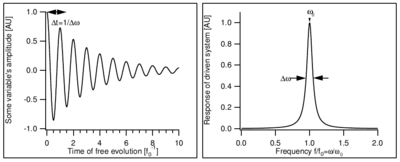
Classically, a resonance is a system where one or more variables change periodically such that when the system is no longer driven by an extended periodic process, the decay of the system's oscillation takes many (or at least several) oscillation periods. Equivalently, the response of the driven system as a function of drive frequency exhibits some form of peaked structure. The frequency corresponding to the maximum response of the system is called the resonance frequency ()
A resonance in the time (left) and frequency (right) domains. The time domain picture shows the (decaying) oscillation in some variable of the undriven system, while the frequency-domain pictures shows the steady-state response amplitude of the driven system. The time units are chosen such that while the quality factor is .
The simplest resonance systems have a single resonance frequency, corresponding to the harmonic motion of the variable. Some form of dissipation (damping) results in a finite damping time () for the undriven system, and a finite width () of the resonance curve for the driven system. The quantities and are related by a Fourier transformation: any oscillation with time-varying amplitude must be made up of a superposition of different frequency components, giving the resonance curve a finite width in frequency space. Low dissipation results in a long decay time , and a narrow frequency width . The ratio of frequency width to resonance frequency is called the quality factor .
Atomic physics often deals with isolated atomic systems in a vacuum, providing resonances of high quality factor . For example, an optical transition, even in a room-temperature (ie Doppler-broadened) gas, will have a -factor of
- Failed to parse (unknown function "\unit"): {\displaystyle \frac{f_0}{\Delta f} \sim \frac{\unit{10^{15}}{\hertz}}{\unit{10^9}{\hertz}} \sim 10^6 }
In contrast, high factors in solids typically require cryogenic temperatures: typical factors of mechanical or electrical systems are at room temperature and at Failed to parse (unknown function "\unit"): {\displaystyle \lesssim \unit{1}{\kelvin}} temperatures.
High Q values are obtained in solids acting as optical resonators: has been achieved in the whispering gallery modes of spheres or cylinders of high-purity glass [1].
One of the whispering-gallery resonators described in [1]. This particular resonator had a quality factor . The very high surface quality required for such low losses is achieved by having surface tension shape the rim of the disk after it has been temporarily liquefied by a laser pulse; the inset shows the resonator before this treatment.
At the macroscopic scale, astronomical systems consisting of massive bodies travelling essentially undisturbed through the near-vacuum of space can also exhibit high factors. The rotation of the earth has a value of , and pulsars of .
A resonance is particularly useful for science and technology if it is reproducible by different realizations of the same system, and if it has a well-understood theoretical connection to fundamental constants. In atomic physics, quantum mechanics ensures both features: atoms of the same species are fundamentally identical (although the probing apparatus is not), and the quantum mechanical description of atomic structure is well understood and highly accurate, at least for atoms with not too many electrons. The resonance frequencies of hydrogen, and to a lesser degree helium, are directly tied via quantum mechanics to fundamental constants such as the Rydberg constant, Failed to parse (unknown function "\unit"): {\displaystyle R_\infty=\unit{1.0973731568525(73)\times10^7}{\reciprocal\metre}} [2], or the fine structure constant [2]. In fact, the Rydberg constant is the most accurately known constant in all of physics, and most fundamental constants have been determined by atomic physics or optical techniques. Additional motivation for measuring fundamental constants with ever-increasing accuracy has been provided by the speculation (and claims of evidence for it [3][4]), that the fundamental constants may not be so constant after all, but that their value is tied to the evolution (and therefore the age) of the universe. Furthermore unexpected resonances, or splittings of resonances, have in the past indicated the need for new theories or modifications of theories. For instance, "anomalous" effects in the Zeeman structure (magnetic-field dependance) of atomic lines led to the discovery of spin [5]. while Lamb's measurement of the splitting between the and states of atomic hydrogen, on the order of 1000MHz instead of 0 as predicted by the Dirac theory, fostered the development of quantum electrodynamics, the quantum theory of light.
Classical Harmonic Oscillator
A classical harmonic oscillator (HO) is a system described by the second order differential equation
such as a mass on a spring, or a charge, voltage, or current in an electric RLC resonant circuit. For weak damping () the undriven system decays with an exponential envelope,
with . In the cases we will consider, so that . The decay rate constant for the amplitude is , while for the stored energy it is , i.e. the stored energy decays exponentially with a time constant . If the harmonic oscillator is driven at a frequency close to resonance, , the amplitude response is a lorentzian:
where is the detuning as shown on the right-hand side of Figure \ref{fig:example_resonances}. The full width at half maximum (FWHM) of a lorentzian curve is leading to a quality factor
Note that , , and are measured in angular frequency units \unit{\radian\per\second}, or \unit{\reciprocal\second} for short, and should not be confused with frequencies , etc. When quoting values, we will often write explicitly Failed to parse (unknown function "\unit"): {\displaystyle \omega_0=2\pi\times\unit{1}{\mega\hertz}} rather than Failed to parse (unknown function "\unit"): {\displaystyle \omega_0=\unit{6.28\times10^6}{\reciprocal\second}} to remind ourselves that the quantity in question is an angular frequency. We will never write Failed to parse (unknown function "\unit"): {\displaystyle \omega_0=\unit{6.28\times10^6}{Hz}} : although formally dimensionally consistent, this invites confusion with real (laboratory or Hertzian) frequencies. For brevity, we will often write or say "frequency" when we mean angular frequency, but will quote real frequencies as Failed to parse (unknown function "\unit"): {\displaystyle f_0=\unit{1}{\mega\hertz}} . Note that the natural unit for decay rate constants is that of an angular frequency, as in . Therefore we will express decay rates as inverse times in angular frequency units: Failed to parse (unknown function "\unit"): {\displaystyle \gamma=\unit{10^4}{\reciprocal\second}} for instance, but not Failed to parse (unknown function "\unit"): {\displaystyle \gamma=\unit{10^4}{\hertz}} , nor Failed to parse (unknown function "\unit"): {\displaystyle \gamma=2\pi\times\unit{1.6}{\kilo\hertz}} . Damping time constants are the inverse of decay rate constants, Failed to parse (unknown function "\unit"): {\displaystyle \tau=1/\gamma=\unit{100}{\micro\second}} .
Resonance Widths and Uncertainty Relations
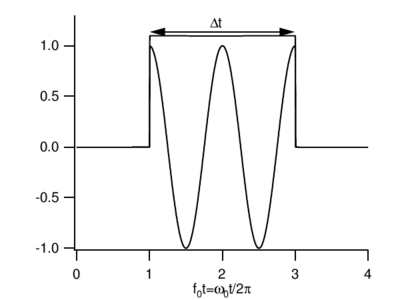
From it follows that damping time and the resonance linewidth of the driven system obey: or, assuming , : a finite number of frequency components or energies () is necessary to synthesize a pulse of finite () width in time.
Measurement in a limited time , modelled as an ideal monochromatic sine wave of frequency gated by an observation window of finite width
This is quite similar to an uncertainty relation familiar from Fourier transformation theory, according to which the measurement of a frequency in a finite time (see Figure \ref{fig:gated_pulse}) results in a frequency spread obeying . By using we can further connect this with the usual Heisenberg uncertainty relation
Question: {q:classical_line_splitting} Does the Heisenberg uncertainty relation , or rather the frequency uncertainty relation that follows from (classical) Fourier theory hold in classical systems? Can you measure the angular frequency of a classical harmonic oscillator in a time with an accuracy better than ?
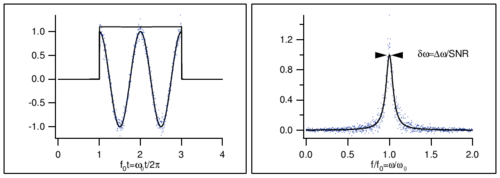
Answer: Yes - if you have a good model for the signal, for instance if you know that it is a pure sine wave, and if the signal to noise ratio (SNR) of the measurement is good enough, then you can fit the sine wave's frequency to much better accuracy than its spectral width (see Fig. \ref{fig:line_splitting}). As a general rule, the line center can be found to within an uncertainty . This is known as splitting the line. Splitting the line by a factor of 100 is fairly straightforward, splitting it by a factor of a 1000 is a real challenge. As an extreme example of this, Caesium fountain clocks interrogate a 9 GHz transition for a typical measurement time of 1 s, yielding , but the best ones can nonetheless achieve relative accuracies of [6]. Of course, this sort of performance requires a very good understanding of the line shape and of systematics.
Splitting the line in time and frequency domains. Given a sufficiently good model of the signal or line shape, and adequate signal-to-noise, one can find the center frequency of the underlying signal to much better than or the line width.
Question: {q:quantum_line_splitting} Can you measure the angular frequency of a quantum mechanical harmonic oscillator in a time to better than ?
Question: {q:laser_line_splitting} Can you measure the angular frequency of a laser pulse lasting a time to better than ?
If you answered \ref{q:quantum_line_splitting} and \ref{q:classical_line_splitting} differently, you may have a problem with \ref{q:laser_line_splitting}. Is a laser pulse quantum or classical? Clearly it is possible to beat for a laser pulse. For instance, you can superimpose the laser pulse with a laser of fixed and known frequency on a photodiode, and fit the observed beat note. The stronger the probe pulse, the better the SNR of the beat note, and the more accurately you can extract the probe frequency. So how are we to reconcile quantum mechanics and classical mechanics, and what does the Heisenberg uncertainty really state?
The Heisenberg uncertainty relation makes a statement about predicting the outcome of a single measurement on a single system. For a single photon, the limit does indeed hold. However, nothing in quantum mechanics says that you cannot improve your knowledge about the average values of the quantities characterizing the system by repeated measurements on identical copies of it. In the laser example above, the frequency resolution improves with probe pulse strength because we are measuring many photons - for the purposes of this discussion we could have measured the frequencies of the photons sequentially.
For independent measurement of uncorrelated photons the SNR is given by : the signal grows as , while the noise is the shot noise of the photon number, which grows as . This SNR allows a frequency uncertainty of , known as the standard quantum limit. If we allow the use of entangled or correlated states of the photons, then the uncertainty can be as low as the Heisenberg limit [7][8].
Let us now revisit \ref{q:quantum_line_splitting}. You may have heard that the quantum mechanical description of electromagnetism, quantum electrodynamics (QED), represents any single mode of the electromagnetic field by a harmonic oscillator of the same frequency. The ground state corresponds to no photons in the mode, the first excited state to one photon and so forth. This description is valid because photons to a very good approximation do not interact: the addition of a photon changes the system's energy always by the same increment. Since the many-photon pulse from \ref{q:laser_line_splitting} maps onto a quantum harmonic oscillator, it seems to follow that \ref{q:quantum_line_splitting} must also be answered in the affirmative.
On the other hand, a harmonic oscillator is a single quantum system to which the Heisenberg limit must apply. The resolution of this apparent contradiction is that \ref{q:quantum_line_splitting} is asking about a measurement of the fundamental frequency of the harmonic oscillator, not the energy of a particular level. Therefore if you measure the energy of the n-th level to , which can be done by exciting the -th level from the ground state through a nonlinear process, then the uncertainty on the harmonic oscillator resonance frequency (that corresponds to the laser frequency in \ref{q:quantum_line_splitting}) is given by .
If the interaction with the oscillator is restricted to classical fields or forces, then there is an additional uncertainty of on which particular level of the oscillator is being measured and so we recover the standard quantum limit mentioned previously.
Magnetic Resonance: The Classical Magnetic Moment in a Spatially Uniform Field
Harmonic oscillator versus two-level systems
Now, unlike in classical mechanics, most resonances studied in atomic physics are not harmonic oscillators, but two-level systems. Unlike harmonic oscillators, two-level systems show saturation. When a harmonic oscillator is driven longer or faster, higher and higher excited states are populated: the oscillator amplitude can become arbitrarily large. In contrast, the amplitude of oscillation in a two-level system is limited to one half in the appropriate dimensionless units.(An analogous dimensionless amplitude for the harmonic oscillator would be the amplitude measured in units of the oscillator ground state size.)
Why, and under what conditions, do classical harmonic oscillator models of a two-level system work? A two-level system of energy difference can be approximated by a harmonic oscillator of frequency when saturation effects in the two-level system are negligible, i.e. when the population of the second excited state in the harmonic oscillator problem is negligible, or equivalently when the population ratio of the first excited state to the the ground state is small: . This is the basis for the classical Lorentz model of the electron bound in the atom that describes many linear atomic properties (for instance the refractive index) very well. See "The origin of the refractive index" in chapter 31 of the Feynman Lectures on Physics [9].
When saturation comes into play, i.e. when the initial ground state is appreciably depleted, the harmonic oscillator ceases to be a good model. The limit on the oscillation amplitude in a two-level system suggests that a classical system with periodic evolution and a limit on the amplitude, namely rotation, could provide a better classical model of a two-level system. Indeed, the motion of a classical magnetic moment in a uniform field provides a model that captures almost all features of the quantum-mechanical two-level system, the exception being the projection onto one of the two possible outcomes in a measurement.
Magnetic Moment in a Static Field
The interaction energy of a magnetic moment with a magnetic field is given by
In a uniform field the force
vanishes, but the torque
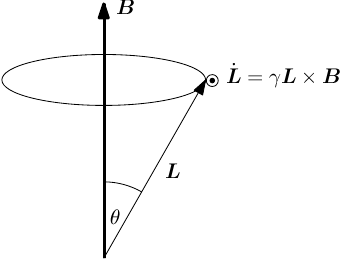
does not. For an angular momentum the equation of motion is then
where we have introduced the gyromagnetic ratio as the proportionality constant between angular momentum and magnetic moment, as shown in Figure \ref{fig:static_precession}.
{fig:static_precession} Precession of a the magnetic moment and associated angular momentum about a static field .
This describes the precession of the magnetic moment about the magnetic field with angular frequency
is known as the Larmor frequency. For electrons we have Failed to parse (unknown function "\unit"): {\displaystyle \gamma_e=2\pi\times\unit{2.8}{\mega\hertz\per G}} , for protons Failed to parse (unknown function "\unit"): {\displaystyle \gamma_p=2\pi\times\unit{4.2}{\kilo\hertz\per G}} .
Transformation to a Rotating Coordinate System
A vector rotating at constant angular velocity is described by
Then the rates of change of measured in a coordinate system rotating at and in an inertial system are related by
This follows immediately from the following facts:
- If is constant in the rotating system then .
- If then .
- Coordinate rotation is a linear transformation.
This transformation is sometimes abbreviated as the schematic rule
It follows that the angular momentum in a rotating frame obeys
If we choose , then is constant in the rotating frame. Often it is useful to think of a fictitious magnetic field that appears in a rotating frame.
Larmor's Theorem for a Charged Particle in a Magnetic Field
The vanishing of the torque on a magnetic moment when viewed in the correct rotating frame is reminiscent of Larmor's theorem for the motion of a charged particle in a magnetic field, which we now present.
According to answers.com, Lamor's theorem can be stated as For a system of charged particles, all having the same ratio of charge to mass, moving in a central field of force, the motion in a uniform magnetic induction B is, to first order in B, the same as a possible motion in the absence of B except for the superposition of a common precession of angular frequency equal to the Larmor frequency.
If the Lorentz force acts in an inertial frame,
then in the rotating frame, according to the rule \ref{eqn:rot_frame_transformation} we have
resulting in a force in the rotating frame given by
where we have used . Choosing
yields
if the field is not too large. Thus the Lorentz force approximately disappears in the rotating frame.
Although Larmor's theorem is suggestive of the rotating co-ordinate transformation, it is important to realize that the two transformations, though identical in form, apply to fundamentally different systems. A magnetic moment is not necessarily charged- for example a neutral atom can have a net magnetic moment, and the neutron possesses a magnetic moment in spite of being neutral - and it experiences no net force in a uniform magnetic field. Furthermore, the rotating co-ordinate transformation is exact for a magnetic moment, whereas Larmor's theorem for the motion of a charged particle is only valid when the term is neglected.
Note: A breakdown of Larmor's theorem occurs for free electrons. Free electrons orbit in a magnetic field at the cyclotron frequency which is twice Larmor's frequency. The reason is that the orbiting velocity is now given by . As can be seen in the equation above, in this case, the centrifugal force equals minus one half of the Coriolis force, and therefore twice the frequency of the rotating frame is needed to cancel the effects of the applied magnetic field.
Rotating Magnetic Field on Resonance
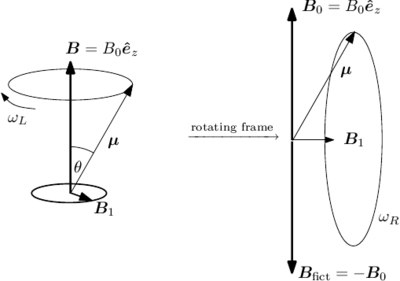
{fig:rotating_frame} Field and moment vectors in the static and rotating frames for the case of resonant drive.
Consider a magnetic moment precessing about a field with in spherical coordinates, where . Assume that we now apply an additional field , in the -plane rotating at . To solve the resulting problem it is simplest to go into the rotating frame (Figure \ref{fig:rotating_frame}). Then is stationary, say along , and there is an additional fictitious field which cancels the field . So in the rotating frame we are left just with the static field , and the magnetic moment precesses about at the Rabi frequency
A magnetic moment initially along the axis will point along the axis at a time given by , while a magnetic moment parallel or antiparallel to the applied magnetic field does not precess in the rotating frame.
Question: {q:rabi_freq_blue_detuned} Assume the magnetic moment is initially pointing along the axis. Assume that a rotating field is applied, but that it rotates at a frequency , where is the Larmor frequency for the static field . Compared to the on-resonant case, , is the oscillation frequency of the magnetic moment.
- larger
- the same
- smaller
Question: Same question as \ref{q:rabi_freq_blue_detuned} but for .
Rotating Magnetic Field Off-Resonance
If the rotation frequency of does not equal the Larmor frequency associated with the static field , then in the frame rotating with at frequency the static field is not completely cancelled by the fictitious field , but a difference along remains, giving rise to a total effective field in the rotating frame
The effective field is static, lies at an angle with the z
and is of magnitude
The magnetic moment precesses around it with an effective (sometimes called generalized) Rabi frequency
where is the Rabi frequency associated with , and is the detuning from resonance with the Larmor frequency .
Geometrical Solution for the Classical Magnetic Moment in Static and Rotating Fields
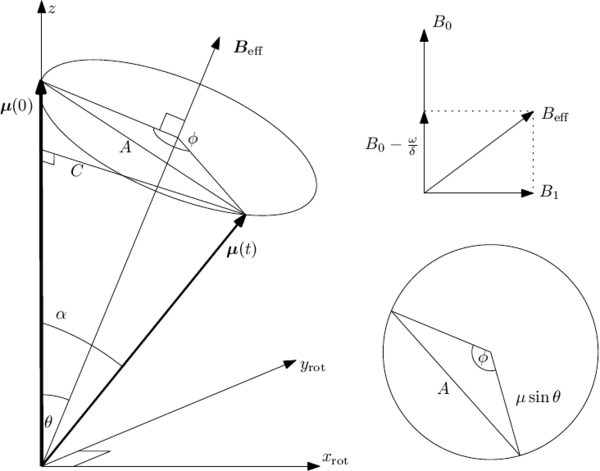
{fig:rotating_coord_construction} Geometrical relations for the spin in combined static and rotating magnetic fields, viewed in the frame co-rotating with the drive field . At lower right is a view looking straight down the axis.
Referring to Figure \ref{fig:rotating_coord_construction}, we have
On the other hand
so that
- {eq:classical_rabi_flopping}
With the Larmor frequency of the static field, the detuning, the resonant and the generalized Rabi frequencies. Note that the precession is faster, but the amplitude smaller for an off-resonant field than for the resonant case. The above result is also the correct quantum-mechanical result.
If we define the quantity , we obtain
In the quantum mechanical treatment (see below), is the probability to find the system in the second state, or the spin flip probability.
"Rapid" Adiabiatic Passage (Classical Treatment)
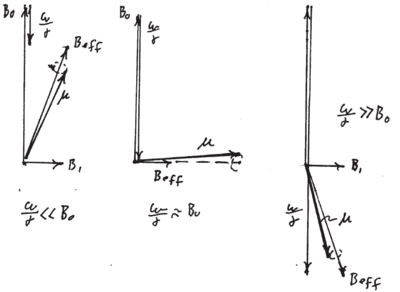
Rapid adiabatic passage is a technique for inverting a spin by (slowly) sweeping the detuning of a drive field through resonance. "Slowly" means slowly compared to the Larmor frequency about the effective static field in the rotating frame for all times ("Rapid" means fast compared to relaxation processes which we neglect here).
The physical picture is as follows. Assume the detuning is initially negative (, ). Since
the effective magnetic field initially points of a small angle relative to the axis. If the detuning is increased slowly compared to the Larmor frequency, the spin will continue to precess tightly around , which for points along the x axis, and for along the axis (see Figure \ref{fig:rapid_adiabatic_passage}).
{fig:rapid_adiabatic_passage} {Motion of the spin during rapid adiabatic passage, viewed in the frame rotating with . The spin's rapid precession locks it to the direction of and thus it is dragged through an angle as the frequency is swept through resonance.
Thus the magnetic moment, starting out along , ends up pointing along . Note that in the rotating frame remains always (almost) parallel to the effective field . A similar precess is used in magnetic traps for atoms, but there is a real, spatially dependent field constant in time. As the atom moves in this field, the fast precession of the magnetic moment about the local field keeps its direction locked to the local field, whose direction varies in the lab frame. Returning to rapid adiabatic passage, since the generalized Rabi frequency is smallest and equal to the resonant Rabi frequency at , the adiabatic requirement is most severe there, i.e. near . Near we have, with ,
where the exclamation point in indicates a requirement which we impose. Consequently, if the evolution is to be adiabatic, we must have . This means that the change of rotation frequency per Rabi period , , must be small compared to the Rabi frequency .
Note that the inversion of the spin is independent of whether is swept up or down through the resonance.
Quantized Spin in a Magnetic Field
Equation of Motion for the Expectation Value
For the system we have been considering, the Hamiltonian is
Recalling the Heisenberg equation of motion for any operator is
where the last term refers to operators with an explicit time dependence, we have in this instance
Using with the Levi-Civita symbol , we have
or in short
These are just like the classical equations of motion \ref{eq:classical_precession_in_static_field}, but here they describe the precession of the operator for the magnetic moment or for the angular momentum about the magnetic field at the (Larmor) angular frequency .
Note that:
- Just as in the classical model, these operator equations are exact; we have not neglected any higher order terms.
- Since the equations of motion hold for the operator, they must hold for the expectation value
- We have not made use of any special relations for a spin- system, but just the general commutation relation for angular momentum. Therefore the result, precession about the magnetic field at the Larmor frequency, remains true for any value of angular momentum .
- A spin- system has two energy levels, and the two-level problem with coupling between two levels can be mapped onto the problem for a spin in a magnetic field, for which we have developed a good classical intuition.
- If coupling between two or more angular momenta or spins within an atom results in an angular momentum , the time evolution of this angular momentum in an external field is governed by the same physics as for the two-level system. This is true as long as the applied magnetic field is not large enough to break the coupling between the angular momenta; a situation known as the Zeeman regime. Note that if the coupled angular momenta have different gyromagnetic ratios, the gyromagnetic ratio for the composite angular momentum is different from those of the constituents.
- For large magnetic field the interaction of the individual constituents with the magnetic field dominates, and they precess separately about the magnetic field. This is the Paschen-Back regime.
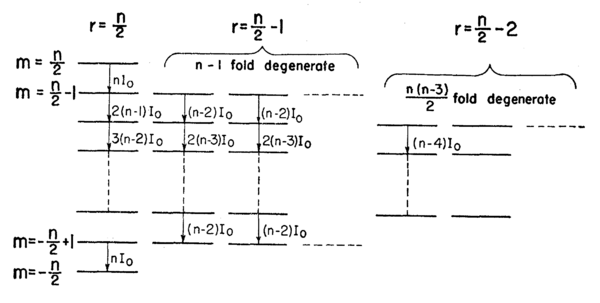
- An even more interesting composite angular momentum arises when two-level atoms are coupled symmetrically to an external field. In this case we have an effective angular momentum for the symmetric coupling:
Level structure diagram for two-level atoms in a basis of symmetric states [10]. The leftmost column corresponds to an effective spin- object. Other columns correspond to manifolds of symmetric states of the atoms with lower total effective angular momentum.
- Again the equation of motion for the composite angular momentum is a precession. This is the problem considered in Dicke's famous paper [10], in which he shows that this collective precession can give rise to massively enhanced couplings to external fields ("superradiance") due to constructive interference between the individual atoms.
The Two-Level System: Spin-1/2
Let us now specialize to the two-level system and calculate the time evolution of the occupation probabilities for the two levels.
{fig:two_level_spin_half} Equivalence of two-level system with spin-. Note that for the spin-up state (spin aligned with field) is the ground state. For an electron, with , spin-up is the excited state. Be careful, as both conventions are used in the literature.
We have that
where in the last equation we have used the fact that . The signs are chosen for a spin with , such as a proton (Figure \ref{fig:two_level_spin_half}). For an electron, or any other spin with , the analysis would be the same but for the opposite sign of and the corresponding exchange of and . If the system is initially in the ground state, (or the spin along , ), the expectation value obeys the classical equation of motion \ref{eq:classical_rabi_flopping}:
- {eqn:rabi_transition_probability}
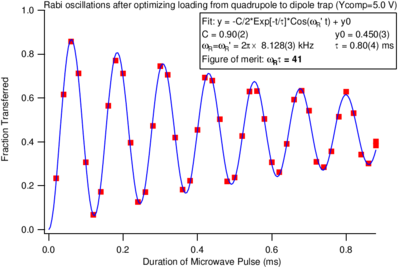
Equation \ref{eqn:rabi_transition_probability} is the probability to find system in the excited state at time if it was in ground state at time . Figure \ref{fig:rabi_signal} shows a real-world example of such an oscillation.
{fig:rabi_signal} Rabi oscillation signal taken in the Vuleti\'{c} lab shortly after this topic was covered in lecture in 2008. The amplitude of the oscillations decays with time due to spatial variations in the strength of the drive field (and hence of the Rabi frequency), so that the different atoms drift out of phase with each other.
Matrix form of Hamiltonian
With the matrix representation
we can write the Hamiltonian associated with the static field as
where is the Larmor frequency, and
is a Pauli spin matrix. The eigenstates are , with eigenenergies . A spin initially along , corresponding to
evolves in time as
which describes a precession with angluar frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0} . The field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _1} , rotating at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} in the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X-Y} plane corresponds to
where have used the Pauli spin matrices Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_x} , . The full Hamiltonian is thus given by
- {eq:dressed_atom_hamiltonian}
This is the famous "dressed atom" Hamiltonian in the so-called "rotating wave approximation". However, note that in the treatment here there are no approximations; it is exact. Its eigenstates and eigenvalues provide a very elegant, very intuitive solution to the two-state problem.
Solution of the Schrodinger Equation for Spin-1/2 in the Rotating Frame
The time-dependence of the above Hamiltonian can be eliminated by applying a unitary transformation to the system. Namely, a rotation about the z-axis accomplishes this. Call this rotation operator , which can be expressed
where we let . Then the transformed Hamiltonian
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} H' = {\bf{R}}H\,{\bf{R}}^{\dagger}-i\hbar\,{\bf{R}}\frac{d\bf{R}^{\dagger}}{dt}, \end{align}}
is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} H' &= \frac{\hbar}{2} \begin{pmatrix} \delta & \omega_{\rm{R}} \\ \omega_{\rm{R}} & -\delta \end{pmatrix}, \end{align}}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta = \omega_0 - \omega} . This time-independent Hamiltonian can be diagonalized exactly to obtain the eigenenergies and eigenstates. The general solution has the form,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \psi(t) = a_g(t) | g \rangle + a_e(t) | e \rangle. \end{align}}
In particular, the case and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_e(0) = 0} leads to the probability of finding the atom in the excited state to be
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} P_e(t) = |a_e(t)|^2 = \frac{\omega^2_{\rm R}}{\Omega^2_{\rm R}} \sin^2 \left( \frac{\Omega_{\rm R} t}{2} \right), \end{align}}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_{\rm R} = \sqrt{\delta^2 + \omega^2_{\rm R}}} is the generalized Rabi frequency. This form is identical to the one obtained in the classical picture.
Solution of the Schrodinger Equation for Spin-1/2 in the Interaction Representation
The same system can be solved by a more brute-force method by isolating the "bare" time-dependence first and then using substitutions. The interaction representation consists of expanding the state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\psi(t)\right\rangle } in terms of the eigenstates , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|g\right\rangle } of the Hamiltonian Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} , including their known time dependence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{iH_0 t/\hbar}} due to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} . That means we write here
Substituting this into the Schrodinger equation
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{d}{dt} \left|\psi(t)\right\rangle =\left(H_0+H_1\right) \left|\psi(t)\right\rangle }
then results in the equations of motion for the coefficients
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\dot{a}_g&= \frac{\omega_R}{2}e^{-i\left(\omega_0-\omega\right)t}a_e \\ i\dot{a}_e&= \frac{\omega_R}{2}e^{i\left(\omega_0-\omega\right)t}a_g \end{align}}
Where we have used the matrix form of the Hamiltonian, \ref{eq:dressed_atom_hamiltonian}. Introducing the detuning Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta=\omega-\omega_0} , we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\dot{a}_g&= \frac{\omega_R}{2}e^{i\delta t}a_e \\ i\dot{a}_e&= \frac{\omega_R}{2}e^{-i\delta t}a_g \end{align}}
The explicit time dependence can be eliminated by the substitution
As you will show (or have shown) in the problem set, this leads to solutions for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_{g,e}} given by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} b_g(t)&= e^{i\Omega_R t/2}B_1+e^{-i\Omega_R t/2}B_2 \\ b_e(t)&= \frac{\omega_R}{\delta-\Omega_R}e^{i\Omega_R t/2}B_1 +\frac{\omega_R}{\delta+\Omega_R}e^{-i\Omega_R t/2}B_2 \end{align}}
with two constants that are determined by the initial conditions. For Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_g(t=0)=1} we find
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| a_e(t)\right| ^2=\frac{\omega_R^2}{\Omega_R^2}\sin^2\frac{\Omega_R t}{2} }
as already derived from the fact that the expectation value for the magnetic moment obeys the classical equation.
"Rapid" Adiabiatic Passage (Quantum Treatment)
Quantum mechanically, we have seen that the Hamiltonian of an interacting two-level system can be written as
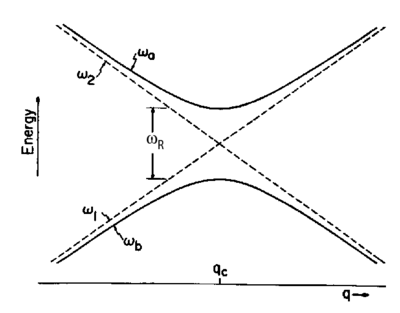
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \equiv \omega - \omega_0} . Let us call the "bare" i.e. unperturbed, eigenstates of the Hamiltonian as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\uparrow \rangle} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\downarrow \rangle} . If you examine the eigenstates of this Hamiltonian, you will realize that by changing the frequency of your coupling, the eigenstates will "evolve" from e.g. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\uparrow \rangle} to , or vice versa. This can be accomplished by sweeping Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} at a rate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\omega}} . This leads to the Landau-Zener problem of a sweep through an avoided crossing.
An avoided crossing. A system on one level can jump to the other if the parameter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} that governs the energy levels is swept sufficiently rapidly.
Whether or not the system follows an energy level adiabatically depends on how rapidly the energy is changed, compared to the minimum energy separation. To cast the problem in quantum mechanical terms, imagine two non-interacting states whose energy separation, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} , depends on some parameter which varies linearly in time, and vanishes for some value Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} . Now add a perturbation having an off-diagonal matrix element Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} which is independent of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , so that the energies at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} are Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm~V =\pm \hbar \omega_{\rm R}/2} . The probability that the system will "jump" from one adiabatic level to the other after passing through the "avoided crossing" (i.e., the probability of non-adiabatic behavior) is
where
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = \frac{| \omega_{\rm R} | ^2}{4 \dot\omega}, }
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot\omega \equiv d\omega /dt} . This result was originally obtained by Landau and Zener. The jumping of a system as it travels across an avoided crossing is called the Landau-Zener effect. Inserting the parameters for our magnetic field problem, we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm na} = \exp \left( -\frac{\pi}{2} \frac{\omega_R^2} {\left| \dot\omega\right|}\right) }
Note that when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^2_{\rm R} \gg \left| \dot\omega\right|} is satisfied, the probability of non-adiabatic behavior is exponentially small. This agrees with our classical analysis.
Let us now consider a diabatic sweep, where the probability to make a transition across the crossing is non-negligible, but small. This process can be described by the Schroedinger equation in a coherent way. In particular,
where is the effective sweep duration, or the dephasing time . This is determined by
where . This then gives us . Then we get
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P \approx \omega^2_{\rm R} t^2_{\rm eff} = \omega^2_{\rm R}/\dot{\omega}. }
Note that the sum of the probability to undergo a transition and the probability to not undergo a transition must equal one. This means Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = 1 - P_{\rm na}} . Using our expression for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm na}} we obtained above, we find
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = 1 - P_{\rm na} = 2 \pi \Gamma \approx \frac{\omega^2_{\rm R}}{\dot{\omega}}. }
Therefore we've determined the probability to undergo a diabatic transition two different ways and see that they agree.
Incidentally the "rapid" in adiabatic rapid passage is something of a misnomer. The technique was originally developed in nuclear magnetic resonance in which thermal relaxation effects destroy the spin polarization if one does not invert the population sufficiently rapidly. In the absence of such relaxation processes one can take as long as one pleases to traverse the anticrossings, and the slower the crossing the less the probability of jumping.
Decoherence Processes, Mixed States, Density Matrices
The purely Hamiltonian evolution described by the Schrodinger Equation leaves the system in a pure state. However, often we have to deal with incoherent processes such as the uncontrolled loss or addition of atoms, or other perturbations that change the system evolution in an uncontrollable way. If the incoherent process is merely a (state-dependent) loss of atoms to a third state then we can describe the system by a Hamiltonian with complex eigenstates
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{g,e}\rightarrow E_{g,e}+i\frac{\Gamma_{g,e}t}{2} }
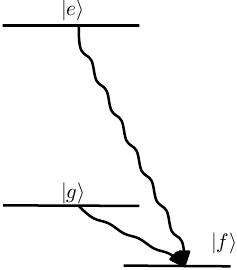
The decay of the norm corresponds to decay out of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|g\right\rangle } , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|e\right\rangle } system, as in figure \ref{fig:decay_out}.
{fig:decay_out} Decay out of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|e\right\rangle} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|g\right\rangle} system, which can be modelled by a non-Hermitian Hamiltonian, the imaginary part of the eigenvalue corresponding to a decay rate.
However, other processes, such as spontaneous decay from to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|g\right\rangle } or loss of coherence (well-defined phase relationship) between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|e\right\rangle } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|g\right\rangle } due to uncontrolled level shifts (e.g. collisions, uncontrolled B-field fluctuations) cannot be dealt with within the Hamiltonian approach and require the density matrix formalism.
Density Operator
The density operator formalism is necessary when the preparation process does not prepare a single quantum state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\psi\right\rangle } , but a statistical mixture of quantum states with probabilities Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_i} . The density operator is the projection operator for that statistical mixture, or ensemble average.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\rho}=\Sigma P_i \left|\psi_i\right\rangle \left\langle \psi_i\right| =\overline{ \left|\psi\right\rangle \left\langle \psi\right| } }
From the Schrodinger equation it follows that the Hamiltonian evolution of the density operator is governed by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\dot{\hat{\rho}}=\left[\hat H,\hat\rho\right] }
In the presence of damping and decay processes there are additional terms, and the time evolution is governed by a so-called Master equation. The expectation value of any operator is given by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \hat O\right\rangle = Tr \left(\hat O\hat \rho\right)= Tr \left(\hat \rho\hat O\right) }
The expectation value of the unity operator must be 1, so The expectation value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat\rho} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Tr \left(\hat \rho^2\right)} , is unity for a pure state , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <1} for a mixed state. In any basis Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \left|n\right\rangle \right\}} , is specified in terms of its matrix elements
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{n^\prime n}= \left\langle n^\prime\right| \hat \rho \left|n\right\rangle }
and the expectation value of any operator can be written as
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \left\langle \hat O\right\rangle &= Tr \left(\hat O\hat\rho\right) =\Sigma_n \left\langle n\right| \hat O\hat \rho \left|n\right\rangle =\Sigma_{n^\prime n} \left\langle n\right| \hat O \left|n^\prime\right\rangle \left\langle n^\prime\right| \hat \rho \left|n\right\rangle \\ \left\langle \hat O\right\rangle &= \Sigma_{nn^\prime}O_{nn^\prime}\rho_{n^\prime n} \text{ with } O_{nn^\prime}= \left\langle n\right| \hat O \left|n^\prime\right\rangle \end{align}}
The diagonal elements of the density matrix (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{n^\prime n}} ) are called the probabilities since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{nn}} is the probability to find the system in state , while the off-diagonal elements are called coherences (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{n^\prime n}} is the coherence between states Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^\prime} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} ). If we write Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{n^\prime n}=Ae^{i\phi}} with , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} real then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{n^\prime n}} is the phase between states Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^\prime} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} , while . The coherence is maximum when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\sqrt{\rho_{nn}\rho_{n^\prime n^\prime}}} . Finally note that the density operator is hermitian, so that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{n^\prime n} = \rho_{nn^\prime}^\star} , as we would expect for a meaningfully-defined coherence between two states.
Density Matrix for a Two-Level System and Bloch Vector
We now introduce a slightly different parametrization of the two-level Hamiltonian \ref{eq:dressed_atom_hamiltonian} and of the corresponding density matrix:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} H&= \frac{\hbar}{2} \begin{pmatrix} \omega_0 & \omega_R e^{-i\omega t} \\ \omega_R e^{i \omega t} & -\omega_0 \end{pmatrix} =\frac{\hbar}{2} \begin{pmatrix} \omega_0 & V_1-iV_2 \\ V_1+iV_2 & -\omega_0 \end{pmatrix} \\ &= \frac{\hbar}{2} \left(V_1\hat\sigma_x+V_2\hat\sigma_y+\omega_0\hat\sigma_z\right) \\ \rho&= \begin{pmatrix} \rho_{11} & \rho_{12} \\ \rho_{21} & \rho_{22} \end{pmatrix} =\frac{1}{2} \begin{pmatrix} r_0+r_3 & r_1-ir_2 \\ r_1+ir_2 & r_0-r_3 \end{pmatrix} \\ &= \frac{1}{2} \left(r_0\hat 1 + r_1\hat\sigma_x + r_2\hat\sigma_y + r_3 \hat\sigma_z\right) \end{align}}
In the problem set you will show (or have shown) that the Hamiltonian evolution of the density matrix
implies the equation of motion
for the vectors and This slightly generalizes our previous result: for a pure state using the Heisenberg equations of motion we had shown that the spin- and the corresponding magnetic moment obey
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d {\bf{S}} }{dt}= {\bf{\omega}} \times {\bf{S}} }
but we have now generalized this result to mixed states, i.e. to ensemble averages that have less than the maximum possible magnetic moment.
We have just derived the theorem by Feynman, Vernon and Hellwarth (1957) which states that the time evolution of the density matrix for the most general two-level system is isomorphic to the behavior of a classical moment in a suitable time-dependent magnetic field.
Note that Hamiltonian evolution does not change the purity of a state: a pure state always remains pure, no matter how violently it is rotated, and a mixed state retains its degree of mixedness (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Tr \rho^2(t)=\text{const.}} ) Here we can check this explicitly by noting that
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Tr \rho^2 =\frac{1}{2}\left(r_0^2+r_1^2+r_2^2+r_3^2\right) =\frac{1}{2}\left(r_0^2+ \left| {{\bf{r}}} \right| ^2\right) }
Since , the length of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{r}} } does not change, and hence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Tr \rho^2} is constant in time.
Phenomenological Treatment of Relaxation: Bloch Equations
Statistical mechanics tells us the form which the density matrix will ultimately take, but it does not tell us how the system will get there or how long it will take. All we know is that ultimately the density matrix will thermalize to
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^T = \frac{1}{Z} e ^{-H_0/kT}, }
where Z is the partition function.
Since the interactions which ultimately bring thermal equilibrium are incoherent processes, the density matrix formulation seems like a natural way to treat them. Unfortunately in most cases these interactions are sufficiently complex that this is done phenomenologically. For example, the equation of motion for the density matrix might be modified by the addition of a damping term:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\rho} = \frac{1}{i\hbar} [H, \rho ] - (\rho - \rho^T)/T_e }
which would (in the absence of a source of non-equilibrium interactions) drive the system to equilibrium with time constant Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_e} .
This equation is not sufficiently general to describe the behavior of most systems studied in resonance physics, which exhibit different decay times for the energy and phase coherence, called and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2} respectively.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_1} - decay time for population differences between non-degenerate levels, e.g. for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_3} (also called the energy decay time).
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2} - decay time for coherences (between either degenerate or non-degenerate states), i.e. for or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_2} .
The reason is that, in general, it requires a weaker interaction to destroy coherence (the relative phase of the coefficients of different states) than to destroy the population difference, so some relaxation processes will relax only the phase, resulting in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2 < T_1} . (caution: certain types of collisions violate this generality.)
The effects of thermal relaxation with the two decay times described above are easily incorporated into the vector model for the 2-level system since the z-component of the population vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}} represents the population difference and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_y} represent coherences (i.e. off-diagonal matrix elements of ): The results are
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\mathbf{r}}_z = \frac{1}{\hbar} {\left( \mathbf{\omega}\times \mathbf{r} \right)_z} - {\left( r_z - r_z^T \right)}/T_1 }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\mathbf{r}}_{x,y} = \frac{1}{\hbar} {\left( \mathbf{\omega}\times \mathbf{r}\right)_{x,y}} - {\left(r_{x,y} - r_{x,y}^T\right)}/T_2 }
For a magnetic spin system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}} corresponds directly to the magnetic moment Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\vec \mu}} . The above equations were first introduced by Bloch in this context and are known as the Bloch equations.
The addition of phenomenological decay times does not generalize the density matrix enough to cover situations where atoms (possibly state-selected) are added or lost to a system. This situation can be covered by the addition of further terms to . Thus a calculation on a resonance experiment in which state-selected atoms are added to a two-level system through a tube which also permits atoms to leave (e.g. a hydrogen maser) might look like
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{\rho} &= \frac{1}{i\hbar} [H, \rho] - \begin{pmatrix} (\rho_{11} - \rho_{11T})/T_1 & \rho_{12}/T_2 \\ \rho_{21}/T_2 & (\rho_{22}- \rho_{22T})/T_1 \end{pmatrix} +R \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} - \rho /T_{\rm escape} - \rho /T_{\rm collision} \end{align} }
where R is the rate of addition of state-selected atoms. The last two terms express effects of atom escape from the system and of collisions (e.g. spin exchange) that can't easily be incorporated in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2} .
The terms representing addition or loss of atoms will not have zero trace, and consequently will not maintain TrFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ( \rho ) = 1} . Physically this is reasonable for systems which gain or lose atoms; the application of the density matrix to this case shows its power to deal with complicated situations. In most applications of the above equation, one looks for a steady state solution (with ), so this does not cause problems.
References
- Armani2003: D. K. Armani, T. J. Kippenberg, S. M. Spillane, and K. J. Vahala. Ultra-high-Q toroid microcavity on a chip. Nature, 421:925–928, Feb 2003.
- codata2002: Peter J. Mohr, Barry N. Taylor, and David B. Newell. CODATA recommended values of the fundamental physical constants: 2002. Rev. Mod. Phys., 77, Jan 2005. Available online at http://physics.nist.gov/constants.
- Dicke1954: R. H. Dicke. Coherence in spontaneous radiation processes. Phys. Rev., 93(1):99, Jan 1954.
- Feynman1963: Richard Feynman, Robert B. Leighton, and Matthew L. Sands. The Feynman Lectures on Physics. Addison-Wesley, 1963. 3 volumes.
- Flambaum2004: V. V. Flambaum, D. B. Leinweber, A. W. Thomas, and R. D. Young. Limits on variations of the quark masses, QCD scale, and fine structure constant. Phys. Rev. D, 69(11):115006, 2004.
- Ramsey1949: Norman F. Ramsey. A new molecular beam resonance method. Phys. Rev., 76(7):996, Oct 1949.
- Ramsey1950: Norman F. Ramsey. A molecular beam resonance method with separated oscillating fields. Phys. Rev., 78(6):695–699, Jun 1950.
- Reinhold2006: E. Reinhold, R. Buning, U. Hollenstein, A. Ivanchik, P. Petitjean, and W. Ubachs. Indication of a cosmological variation of the proton-electron mass ratio based on laboratory measurement and reanalysis of h2 spectra. Phys. Rev. Lett., 96:151101, 2006.
- Santarelli1999: G. Santarelli, Ph. Laurent, P. Lemonde, A. Clairon, A. G. Mann, S. Chang, A. N. Luiten, and C. Salomon. Quantum projection noise in an atomic fountain: A high-stability cesium frequency standard. Phys. Rev. Lett., 82:4619, 1999.
- Uhlenbeck1926: G. E. Uhlenbeck and S. Goudsmit. Spinning electrons and the structure of spectra. Nature, 117(2938):264, Feb 1926.
- Wineland1992: D. J. Wineland, J. J. Bollinger, W. M. Itano, F. L. Moore, and D. J. Heinzen. Spin squeezing and reduced quantum noise in spectroscopy. Phys. Rev. A, 46(11):R6797–R6800, Dec 1992.
- Wineland1994: D. J. Wineland, J. J. Bollinger, W. M. Itano, and D. J. Heinzen. Squeezed atomic states and projection noise in spectroscopy. Phys. Rev. A, 50(1):67–88, Jul 1994.
Notes
- ↑ 1.0 1.1 D. K. Armani, T. J. Kippenberg, S. M. Spillane, and K. J. Vahala. Ultra-high-Q toroid microcavity on a chip. Nature, 421:925–928, Feb 2003.
- ↑ 2.0 2.1 Peter J. Mohr, Barry N. Taylor, and David B. Newell. CODATA recommended values of the fundamental physical constants: 2002. Rev. Mod. Phys., 77, Jan 2005. Available online at http://physics.nist.gov/constants.
- ↑ V. V. Flambaum, D. B. Leinweber, A. W. Thomas, and R. D. Young. Limits on variations of the quark masses, QCD scale, and fine structure constant. Phys. Rev. D, 69(11):115006, 2004.
- ↑ E. Reinhold, R. Buning, U. Hollenstein, A. Ivanchik, P. Petitjean, and W. Ubachs. Indication of a cosmological variation of the proton-electron mass ratio based on laboratory measurement and reanalysis of h2 spectra. Phys. Rev. Lett., 96:151101, 2006.
- ↑ G. E. Uhlenbeck and S. Goudsmit. Spinning electrons and the structure of spectra. Nature, 117(2938):264, Feb 1926.
- ↑ G. Santarelli, Ph. Laurent, P. Lemonde, A. Clairon, A. G. Mann, S. Chang, A. N. Luiten, and C. Salomon. Quantum projection noise in an atomic fountain: A high-stability cesium frequency standard. Phys. Rev. Lett., 82:4619, 1999.
- ↑ D. J. Wineland, J. J. Bollinger, W. M. Itano, F. L. Moore, and D. J. Heinzen. Spin squeezing and reduced quantum noise in spectroscopy. Phys. Rev. A, 46(11):R6797–R6800, Dec 1992.
- ↑ D. J. Wineland, J. J. Bollinger, W. M. Itano, and D. J. Heinzen. Squeezed atomic states and projection noise in spectroscopy. Phys. Rev. A, 50(1):67–88, Jul 1994.
- ↑ Richard Feynman, Robert B. Leighton, and Matthew L. Sands. The Feynman Lectures on Physics. Addison-Wesley, 1963. 3 volumes.
- ↑ 10.0 10.1 R. H. Dicke. Coherence in spontaneous radiation processes. Phys. Rev., 93(1):99, Jan 1954.



























































































































































![{\displaystyle {\frac {d}{dt}}{\hat {O}}={\frac {i}{\hbar }}\left[{\hat {H}},{\hat {O}}\right]+{\frac {\partial {\hat {O}}}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae5069cad777556e25ef2674f2ed7f1fbdc641a0)
![{\displaystyle {\frac {d}{dt}}{\hat {\mu }}_{k}=\gamma {\frac {d}{dt}}{\hat {L}}_{k}={\frac {i\gamma }{\hbar }}\left[{\hat {H}},{\hat {L}}_{k}\right]=-{\frac {i\gamma ^{2}}{\hbar }}B_{0}\left[{\hat {L}}_{z},{\hat {L}}_{k}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31c5220d2321caf92920986550a99c6ba69fb523)
![{\displaystyle \left[{\hat {L}}_{k},{\hat {L}}_{l}\right]=i\hbar \epsilon _{klm}{\hat {L}}_{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b0dce00bc29fe901e80ab62151d3d46ed0adb58)













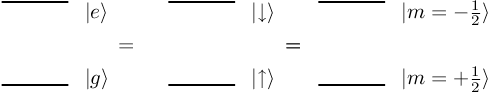













































![{\displaystyle i\hbar {\dot {\rho }}=\left[H_{1},\rho \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e5e259b04bf4e884cca304e93b39186aa4697fe)








