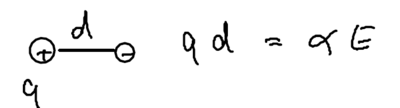Physics of the dipole force: fields and energy

Four physical pictures of the dipole force

Let us recall four different physical pictures for deriving the dipole force:

\begin{itemize}

• Optical Bloch equations.

• Dressed atom picture.

• Classical dipole model of atom, in electric field.

• Macroscopic dielectric object.

\end{itemize}

Classical dipole

The classical dipole model is based on the fact that the force seen by the dipole depends on whether the electric dipole is in-phase or out-of-phase with the driving field $E$. This gives either an attractive or repulsive force.

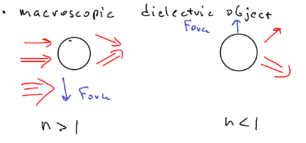
Macroscopic dielectric object

The picture of a macroscopic dielectric object assumes, for example, that you have a microscopic sphere of glass, with a laser beam which is stronger in part of space than another:

So if the microsphere were an atom, with index of refraction greater than one, then the sphere moves toward the field maximum. This is because if you imagine the microsphere is a prism (with index greater than one), then the upper beam is deflected downwards and the lower beam is deflected upwards, such that the sphere acts like a lens. The sphere then is forced to move to compensate for the imbalance in the change of photon momentum of the two refracted beams.

Optical tweezers have made an impact on biology almost as large as the impact of laser cooling on atomic physics. With optical tweezers, one can now manipulate objects within a cell. The people who demonstrated optical tweezers first were the same people who demonstrated laser cooling first: Art Ashkin, who teamed up with Steven Chu, at Bell Labs, in the late 1980's.

Electric and magnetic components of the dipole force

Now a question. We have discussed the stimulated light force, also called the dipole force, or the reactive force. Is this force an {\em electric} force (the force on an electric dipole), a magnetic force (Lorentz force), or both? In other words, imagine an atom is in the potential of the standing wave in an optical lattice. Is the potential due to electric forces or magnetic forces? Intuition says that the force is electric, because the electric force is generally larger than the magnetic one. However, that turns out to be incorrect, and indeed it is the Lorentz force which gives rise to the electric dipole potential. At this point, you may completely appreciate the electric dipole potential, since by writing ${\vec {d}}\cdot {\vec {E}}$ you actually include magnetic forces.

Static fields

In the limit of DC fields, everything does have to be electric, so let us begin with electrostatics. Consider two charges separated by distance $d$:

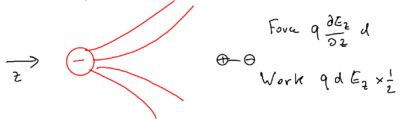
The energy of this configuration is $\alpha E^{2}/2$, due to the polarizability of the atom. Now imagine the charge is placed in an inhomogeneous field:

There is a force on the two halves of the dipole, and the two would cancel unless there is a gradient, so the force on the dipole is

$q{\frac {\partial E_{z}}{\partial z}}d$

so the work done is

${\frac {qdE_{z}}{2}}\,.$

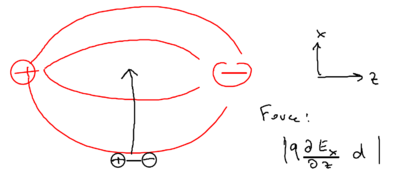
When we move the dipole not along the electric field, but rather, perpendicular to the electric field, consider what happens:

Now, what is the force on the dipole? What matters is the ${\hat {x}}$ component of the force, which is caused by the ${\hat {x}}$ component of the electric field, or more specifically, it matters that the ${\hat {x}}$ component changes by the distance separating the two charges in the dipole.

Now, we want to use the fact that in electrostatics, the curl of the electric field is zero, and therefore by vector calculus,

$\left|q{\frac {\partial E_{z}}{\partial x}}d\right|=\left|q{\frac {\partial E_{z}}{\partial z}}d\right|$

and the work done by moving the dipole in from infinity is $qdE_{z}/2$. This derivation relied on there being no magnetic fields, because otherwise the curl of the electric field would not be zero.

Oscillating fields

Now consider an oscillating dipole in a standing wave, created by counter-propagating laser fields, so that the electric field is perpendicular:

Recall that the potential from the AC Stark shift is $\alpha E^{2}/2$. Let us understand what the force is, which provides this periodic potential. Well, if you have a plane standing wave, that means you can draw the above picture extended up and down. What is the electric force on the dipole in that case? The dipole moment and the gradient of the electric field are orthogonal, in this configuration. There is thus no gradient in the field along the direction of the dipole. Thus, in a plane standing wave, the electric force is identically zero, ${\vec {p}}\perp {\vec {\nabla }}E$. So where does the force come from?

It must originate from the Lorentz force. In this scenario, recall that the Lorentz force is ${\vec {v}}\times {\vec {B}}$. There is an oscillating dipole in the scenario. If you take the derivative of the optical dipole potential, the Lorentz force is

$F_{Lorentz}={\frac {d}{dz}}\left({\frac {1}{2}}\alpha E^{2}\right)\,.$

The standing wave has both electric and magnetic components,

${\begin{aligned}{\vec {E}}&=A_{0}{\hat {e}}_{x}\cos kz\sin \omega t\\{\vec {B}}&=-A_{0}{\hat {e}}_{y}\sin kz\cos \omega t\end{aligned}}$

The dipole potential, averaged over a cycle, is

${\frac {1}{2}}\alpha {\bar {E}}^{2}={\frac {1}{4}}\alpha A_{0}^{2}\cos ^{2}kz\,.$

Recall that the dipole moment is $p=\alpha E$. Thus, the Lorentz force is

$q{\frac {\vec {v}}{c}}\times {\vec {B}}={\frac {\dot {\vec {p}}}{c}}\times {\vec {B}}\,.$

Inserting the expression above for the electric field, we thus obtain this expression for the Lorentz force:

$F_{lorentz}={\frac {\alpha }{c}}A_{0}\omega \cos kz\cos \omega _{t}(-A_{0}\sin kz\cos \omega t)\,.$

Now averaging, we find

${\begin{aligned}{\bar {F}}_{lorentz}&=-{\frac {1}{2}}\alpha A_{0}^{2}k\cos kz\sin kz\\&={\frac {d}{dz}}\left({\frac {1}{4}}A_{0}^{2}\cos ^{2}kz\right)\\&={\frac {d}{dt}}\left({\frac {1}{2}}\alpha {\bar {E}}^{2}\right)\,,\end{aligned}}$

where we now recognize the term on the right in the parentheses as the dipole potential.

Thus, we see that the stimulated force can be either electrical, that is of the form $p_{z}\nabla E_{z}$, or magnetic, that is, of the form ${\dot {p}}\times B$, in nature. Each of the two forces may not be curl free, but the sum of both can be.

Energy conservation and dipole forces

When we considered the dipole force earlier, we looked at how it arises from a redistribution of photons. If you have a monochromatic array of beams, the dipole does not arise due to spontaneous emission, but rather, because photons $\hbar \omega$ are taken from one beam and put into another beam. So how can this result in a change of energy for the atom?

Energy conservation in blue molasses picture

Well, energy exchange does occur, because as we saw atoms flying along a blue standing wave, in the picture of "blue molasses," sees a damping force as it walks up the potential hills:

When atoms slow down due to this viscous force, where has the kinetic energy of the atoms gone?

If you have an ordinary molasses, the energy is radiated away. The basic ingredients available, therefore, are photon absorption, stimulated emission, and spontaneous emission. Recall that in Sisyphus cooling, an atom does emit a photon after climbing up a hill. From the upper dressed level, it emits a blue detuned photon, when the sideband splitting is larger. From the lower dressed level, it emits at the top of the potential, at which the sideband splitting is smaller. The upper sideband is emitted at a larger Rabi frequency than the lower sideband.

The principle behind this observation is that spontaneous emission is once again responsible for the removal of entropy involved in the laser cooling process, and energy is removed along with the entropy change.

One way for providing dissipation is thus radiation into the sidebands.

Transient energy conservation picture

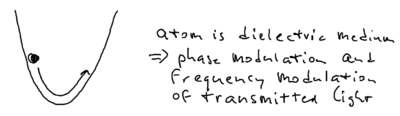
Another scenario for understanding energy conservation is the following transient experiment. Imagine that you have an atom in the harmonic potential of an optical dipole trap.

In extremely far detuned optical lattices, there is essentially no spontaneous emission. The atom oscillating in the dipole trap, say at 1 Hz, going from high to low energy. It is clear this energy must be transformed into the light field, and the question is what actually happens. But it turns out the energy does not emit through spontaneous emission.

What happens is that the moment the atoms reach the bottom of the trap, they have a maximum in energy. The photons which pass through the atom at that point are red shifted. When the atom climbs up the potential hill, the photons are blue shifted. While the atom oscillates, the photons which arrive are blue and red shifted. There is no spontaneous emission in this transient picture, but there is phase modulation of the laser which shifts the laser frequencies.

In principle, this frequency shift should be observable in an experiment. In practice, this is complicated by the fact that real experiments involve spatially inhomogeneous beams, so there is some momentum change as well as phase change of photons involved.