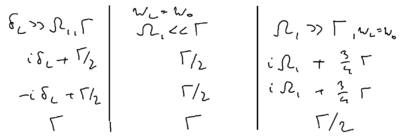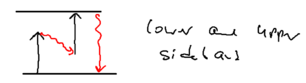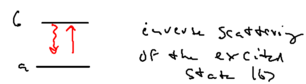Dipole forces and the dressed atom picture
Contents
Dressed Atoms
The dressed atoms picture is one of the most important concepts in modern atomic physics. In this picture, many otherwise complex physical phenomena become clear. For example, we have seen how blue detuned light can perform laser cooling, which was rather counter-intuitive. But if you change basis, and use instead of naked atoms, the dressed atom basis, phenomena such as blue detuned laser cooling become natural and accessible.
The Dressed atoms picture
What is a dressed atom? A dressed atom is an atom plus one mode of the electromagnetic field. We'll come back to that in a moment. On one hand, dressed atoms are nothing new. The dressed atoms picture can be developed from the optical Bloch equations. On the other hand the dressed atoms picture is a language which allows one to better understand what the optical Bloch equations are telling you.
The difference between this treatment, and that of the optical Bloch equations, is that we do not trace out the state of the photon, so we treat the combined state of atom + electromagnetic field. This is actually "half" a difference, because there are two approaches to the dressed atom picture. One emphasizes the photon part of the picture. The second focuses on the atom, treating the electromagnetic field as a classical field. Here, we will focus on the photon, and include the full quantum behavior of the electromagnetic field, at least in setting up the problem.
The dressed atom picture is simply a change of basis. Imagine that you have two pendulums: one representing the atom, the other representing a single electromagnetic mode. From classical mechanics, you know that you can transform in to the basis of the coupled system's eigenmodes. That is what we do in the dressed atom picture. Mathematically, it is almost simplistic, but as you will see it really changes the way you may look at atoms.
Picture of dressed atom scenario
Let us draw a big picture of the Hilbert space we are dealing with:
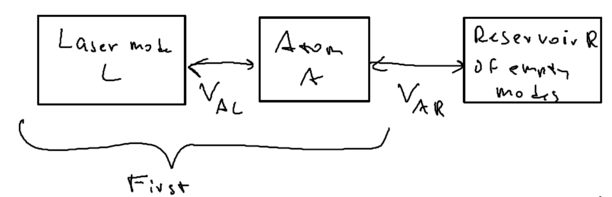
What is central to this picture is the atom. We allow the atom () to be driven by one mode of the (laser's) electromagnetic field . And we allow the atom to also couple to a reservoir of empty modes; this reservoir is what we used in our study of open quantum systems with master equations. The coupling between atom and photon, is just the Jaynes-Cummings interaction. Previously, we put all of these blocks into one picture.
In this treatment, we couple the atom and photon first, as being the stronger interaction which we diagonalize exactly, then consider the coupling of the coupled system with the rest of the world, the reservoir states.
Coupling hamiltonian
That means our Hamiltonian has three parts. We have the photon (a simple Harmonic oscillator), the atom, and the rest of the world. The photon and atom Hamiltonians are:
Our first approximation is that we will only interested in resonant physics rather than off-resonant behavior, so we assume the detuning of the photon from the atom is small, . Our states are labeled by the number of photons , and the states of the two-level atom, and .
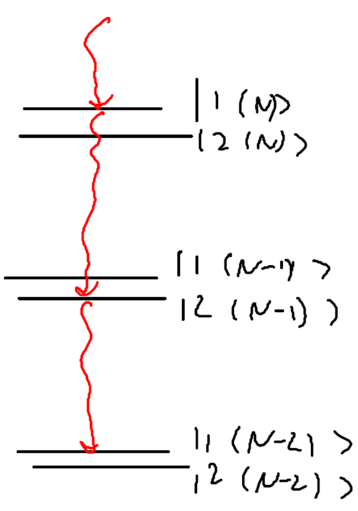
Define the manifold of states as being , the set of states with total energy . Drawn as energy levels, this is
Our path to the dressed atom picture is thus clearly that we want to diagonalize the coupling in terms of these state manifolds of constant total energy. The coupling Hamiltonian is
The electric field operator is
The dipole operator is
The coupling constant describing this interaction is thus
Energy level splitting at large energy
We apply the coupling Hamiltonian to the two states within each manifold , obtaining the matrix elements
Now we need to consider that we have couplings not only between the two states of the manifold, but also states between manifolds, in the following way. That is, in the rotating wave approximation, we raise the photon number by one and lower the atom. But there are also counter-rotating terms, which raise the photon number while also exciting the atom, or which lower the photon number while also de-exciting the atom. That is, can coupled to , and can couple to . However, these lead to an energy change of two quanta, which are less likely to occur than resonant interactions. We thus neglect such off-shell interactions, with the same rationale as used in the rotating wave approximation.
The couplings of pairs of levels within the manifolds are different, and grow as , and we have seen how this gave rise to the collapse and revival of the photon field as seen in the previous study of the Jaynes-Cummings interaction.
Here we take a different approach, and assume that is large, so that we may approximate , so that the couplings are approximately all the same, , where is the average photon number. We then define the Rabi frequency as
where
The Hamiltonian for each manifold thus becomes, in this approximation,
This is the Hamiltonian for a coupled-Hamiltonian system.
Eigenenergies and anti-crossings
Note that we are presenting the dressed atom picture as a solution of a time-independent Hamiltonian. The solution, giving the stationary states under this coupled evolution, has a generalized Rabi frequency
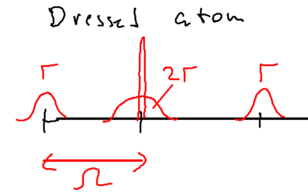
Pictorially, before the coupling the splitting of energy levels in manifold is , and when the coupling is included the splitting is :
The eigenstates are
where .
Consider the following picture of the energy of the system as a function of the laser frequency , where we take the energy of to be zero:
Note that the energy of the state does not depend on the energy of the laser, while the energy of the state grows linearly with . In the dressed atom picture, the crossing (which happens when there is no coupling) splits into an anti-crossing, with a energy splitting of on resonance. The shift between the dressed energy lines (blue) and the naked state lines (red) is just the AC Stark shift.
Emitted light
Consider, as a first example application of the dressed atom picture, the spectrum of the emitted light from an atom excited by a laser beam.
Weak excitation
First, let the incident laser light have weak intensity. What is the spectrum (that is, the frequency dependence) of the radiation scattered from the atom?
To be as simple as possible, let us give the atom infinite mass (or assume it is trapped deeply in a potential well), such that it cannot move. There are several possibilities you might think of as the correct answer to this question.
The first possibility is that the atom emits with a Lorentzian with linewidth at its frequency . The scond possibility is that it emits with a delta function at frequency . A third possibility is that it emits with a delta function at the laser frequency . And a fourth possibility is that it emits with a Lorentzian with linewidth at frequency .
We have monochromatic energy coming into the system at frequency . The experiment scatters the photons then measures energy again. If you forget everything you know about atomic physics but hold on to the principle of energy conservation, then what answer would you expect?
The answer is very, very clear. If you scatter a single photon, its energy should not change because of energy conservation. Many years ago, beautiful experiments were done (Herbert Walther, 10 years ago), it was shown that the emitted light is a delta function at the frequency of the incident laser .
Lorentizian profiles
The weak excitation scenario leads to a delta function scattered light spectrum. Under what circumstances would you expect to see a Lorentzian broadening? Clearly, the strength of light scattered will follow a lorentzian, as the frequency of the laser is scanned across the atom's resonant frequency.
Thus, if you were to take broadband laser light and shine this light on an atom, the atom would mainly scatter light in a Lorentzian profile around its resonant frequency. The atom acts like a filter, in this sense, but the atom does not broaden the light, it selects from the incident light frequencies.
Strong excitation
When the incident light has strong intensity, then the restrictions of energy conservation are loosened because of the possibility of multi-photon scattering. In this case, in the dressed atom picture, the spectrum of the scattered light now appears as a triplet of lines, known as the Mollow triplet:
There is a delta function at , which has a Lorentzian pedestal of full width half max , and two Lorentians sidebands at of width .
Microscopically, there is a correlation evident in the spectrum, where if a single lower sideband photon is emitted, that is followed by an upper sideband photon, thus satisfying energy conservation.
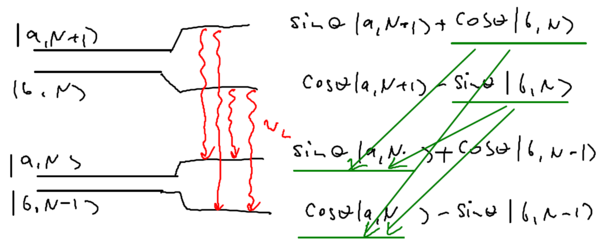
Where does this spectrum come from? Recall the energy levels of the dressed atom picture:
Quantitaive understanding of relative intensities
Keep in mind that the spacing between manifolds is . We can obtain quantitative information about the scattered spectrum with the dressed atom picture. This is because only part of the wavefunction in each superposition state is responsible for the scattered light. For example, a photon emitted from the to has to start from and must end in .
These decompositions tell us what the intensities of the lines in the triplet are. In particular, we can write a table of the transition frequencies and rates expected:
| Frequency | Rate |
Equilibrium populations
The relative intensities are given by population times the rate. We therefore need to obtain the populations of the dressed states. We know that the dressed states are coupled by transitions. If you have the upper and the lower dressed states and can do transitions between them, eventually you reach equilibrium, where the populations are then given by the rate equations.
These rate equations can be written down by inspection:
and similarly for . The time derivatives are zero in steady state, such that
Perspective
Why do we treat the scattered spectrum in such detail here? In part, this is because historically the answer to the scattered spectrum question was something all atomic physicists were expected to know. Today, the methods used are particularly important for what we'll do next. When we discuss light forces in the dressed atom picture, we will need to know how many atoms are in each of the dressed states. This example illustrates how the solution of the two-level system gives you complete answers for such population equations.
Note that there are relaxation rates involved. The actual rate equation looks more like
where the relaxation rate goes as . We shall not solve these in detail here, but in principle such rate equations can be solved, and will be useful for later treatments of scenarios such as laser cooling with blue detuned light.
Peak widths
How does the spectrum evolve from strong excitation to weak excitation? At intensities low compared with saturation, the central peak grows; that is the "coherent peak" due to the weak excitation scattering. As the saturation parameter goes to zero, the fraction of coherent emission grows to become all of the emission.
What are the widths of the three lines? The central feature width is . You can take the rate equations and show that the natural relaxation rates give rise to this width. You can also show how this rate originates from the relative relaxation of the sidebands. But more interestingly, perhaps, you can see how they come from the optical Bloch equations. Recall that these equations are a linear three by three matrix equation, where the transition matrix has certain eigenvalues . There are several regimes of interest:
In the weak excitation limit, recall that the relaxation rates of the Bloch vector along the , , and components are , , and . In the limit of , the eigenvalues are , , and . In the high intensity limit, with and , the dressed atom picture provides the intuition that the Bloch vector is strongly rotated about the axis, so the vector spends half its time along , and half its time along , so its damping rate is the average of and , giving the net damping rate . The axis rate is similar. And the axis average rate is .
Diagramatic approach to high intensity excitation limit
We have now appreciated that any process which results in an emitted spectrum which is not a delta function must be a higher order process. Consider, therefore, the perturbative diagram responsible for the upper and lower sideband emissions:
The inelastic component of the central peak, its broad pedestal, comes from the following process: a photon is emitteed from the excited state, then re-absorbed, with the atom resulting back in the excited state, in a process known as "inverse scattering" from .
Radiative cascade
The radiative cascade is an important concept to understand in the dressed atom picture, for conceptual understanding of laser cooling in the dressed atom picture. We consider it in the uncoupled and dressed state basis.
Uncoupled basis
Consider the diagrams which describe the process of an atom absorbing and emitting a photon:
When an excited atom emits a photon, it cannot emit another photon for some time, given by the inverse Rabi frequency. This gives rise to an anti-bunched spectrum, and also points out the fact that on such short timescales the sidebands of the Mollow triplet cannot be observed.
Dressed atom basis
In the dressed atom basis, each time a photon is emitted, we have converted a photon in our special mode into an excitation in one of the dressed atom manifolds. From the upper dressed state, it can emit either on the carrier, or one of the sidebands, but not the other. Many carrier photons can thus be emitted between sideband photons, but the sideband photons emitted must alternate.











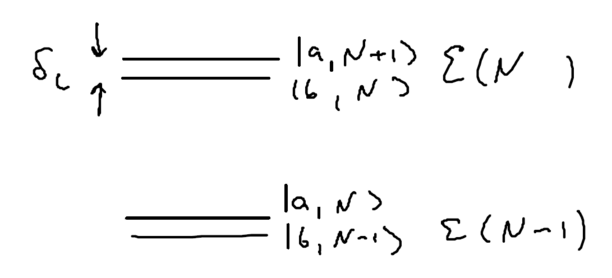
















![{\displaystyle {\frac {\hbar }{2}}\left[{\begin{array}{cc}{-\delta _{L}}&{\Omega _{1}}\\{\Omega _{1}}&{\delta _{L}}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/369cacb5e96c19a15ae6d6300d6b1e433c72d28b)