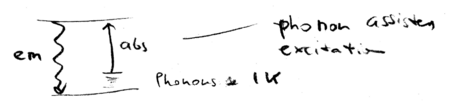Beam Slowing

We have previously looked at cooling with two laser beams, focusing on the idea that if you want to cool, you need a force which is linear with velocity. Now, let us see how you can cool with a single laser beam. That is what you do when you have a single atomic beam. With a single laser beam, you can not only slow them down, but also bunch them up, obtaining the same velocity distribution you get with a molassas. This is the only example of laser cooling I know of which has a very simple, closed form solution, which is possible because there is only one laser beam.

Imagine, if you have a single Lorentzian, how can you cool? Generically, you need a "lock" point, which is stable and has atoms moving to that point in phase space from either velocity direction. With a single beam you don't apparently have such, but as we shall see there is something else interesting that can be done.

Consider a single beam of atoms, with this velocity distribution. Using a laser, you can push some of the atoms to become cooler (red line below), bunching them up in a lower velocity regime, and leaving atoms faster than some velocity unchanged. What do you have to do if you want to bunch all the atoms at zero velocity? It becomes clear that you want more than one laser frequency, for example. By applying a broad range of frequencies which cover the whole velocity distribution, you can slow down all the atoms. There are several techniques using such an approach, known as white light slowing, or diffuse light slowing. But none of those are as powerful as {\em chirpedd slowing} and {\em Zeeman slowing}, the techniques of choice in modener laser cooling.

Chirped slowing

The idea behind chirped slowing is to get the atoms to "ride the surf". In other words, the frequency chirp of the laser beam and the deceleration of the atoms should be synchronized.

Balance of equations

Step 1

The force on an atom in the beam due to the light is

$F=-\hbar k{\frac {\Gamma }{2}}{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta +kv)}{\Gamma }}\right]^{2}}}$

Let $a$ denote the atom's acceleration. Let us assume a frame of reference and experimental setup such that $a<0$, $v>0$, $k>0$, $a_{max}>0$. We can call $\hbar k\Gamma /2=Ma_{max}$, where $M$ is the atom's mass.

Step 2

The scheme begins by selecting the deceleration desired, some $a<0$. Then set $F=-Ma$, and look for a $\delta '=\delta +kv$ to obtain this desired force. This will exist if

$|a|<{\frac {I/I_{0}}{1+I/I_{0}}}a_{max}\,.$

Step 3

Next, select an initial velocity $v_{0}$ such that $v(t)=v_{0}+at$. $\delta '$ is the detuning for this "targeted" velocity group, so we must provide a laser with frequency in the lab frame of $\delta (t)=\delta '-kv(t)$. The atom's velocity will differ from the desired target group by $v'=v-v(t)$.

Step 4

With these definitions, we now have

$F=-\hbar k{\frac {\Gamma }{2}}{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta '+kv')}{\Gamma }}\right]^{2}}}\,,$

in the frame of reference of the atoms in the target velocity group.

Step 5

Transforming into this decelerating frame, we get a fictitious force with is $F_{fict}=-Ma$, and

$F'(v')=Ma_{max}\left[{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta '+kv')}{\Gamma }}\right]^{2}}}+{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta ')}{\Gamma }}\right]^{2}}}\right]$

This second term has the same structure as the first, but it is velocity independent. Note that this is exact, and valid for arbitrary $v'$. All we've done is to substitute definitions, so far, but they provide useful intuition.

Note that for small $v'$, this force is linear in velocity, $F'(v')=-\alpha v'$.

Decelerating Frame

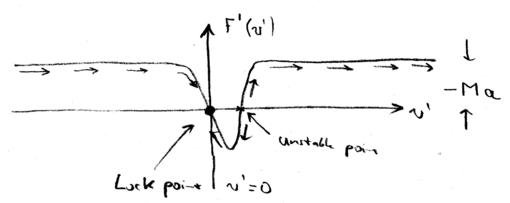
In the lab frame, we have a force which is a positive Lorentzian. In the decelerating frame, we had to add $-Ma$ (the inertial force), so this Lorentzian shifts down, when we plot the total force as a function of the velocity in the decelerating frame $v'$:

Therefore, there is now a stable "lock" point, where $F'=0$ as a function of $v'$. In other words, when the atoms have a negative velocity $v'$, the atoms all accelerate towards zero velocity (in the decelerating frame). And when atoms have a small positive velocity, they also move towards $v'=0$. In contrast the point where the Lorentzian has $F'(v')=0$ at $v'>0$, is unstable.

Thus, we may write, as we did with the molasses, an expression for the linearized force around this point, $F'(v')=-\alpha v'$, in which $\alpha _{beam}=\alpha _{molasses}/2$. There is also randomness, as there was in the optical molassas case, for which we may calculate a momentum diffusion coefficient, and we find that $D_{beam}=D_{molasses}/2$. Thus, the final temperature limit of the beam is actually the same as that achievable with a molasses: $kT_{beam}=kT_{molasses}$.

We've seen that one laser can bunch up atoms from a beam at a single velocity. Physically, what happens is that if the atoms fall behind, the light does not interact with them, but if the atoms are too fast, the laser cools them, much like in the molasses case.

Graphical summary

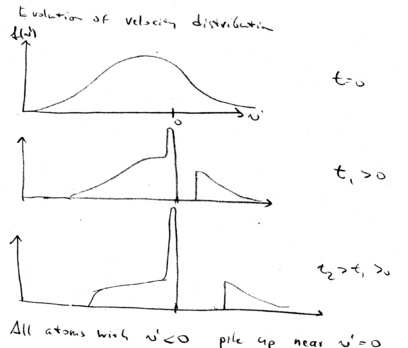
Here is a graphical summary of what we've learned about beam slowing. In the decelerating frame, this is the situation. Change sign, so that in the frame the decelerating force is positive, for this graph:

Initially, our zero force point is at the targeted velocity $v_{0}$. All atoms at larger velocity experience a constant positive force, accelerating them. After a later time $t$, the tail of the maxwell-Boltzmann distribution is pushed to higher velocities. The peak of distribution of atoms grows higher and higher with time, while the positive tail moves to higher velocities.

This is the description in the decelerating frame.

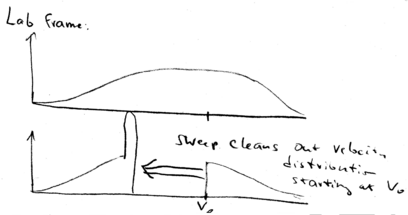
In the lab frame, we shift from $v'$ back to $v$. This means that we just shift all the distributions down in velocity. We start with a broad distribution at $t=0$. There is a velocity group at $t=0$ which is on resonance with the laser beam. As time goes on, the laser beam chirps, causing more and more atoms to come into resonance, piling them up in a lower velocity class. What happens is that after the laser beam is switched off, you may still have a low velocity tail which is not reached by the laser, but you have a huge peak of atoms that have been cooled:

All the atoms at lower velocities are pushed up in velocity until they stack up at $v_{0}$, producing a narrow distribution around $v_{0}$.

The width of this narrow velocity distribution is given by $k_{B}T=D/\alpha$, which is proportional to ${\sqrt {kT_{beam}}}/M$.

Beam cooling is actually the simplest and cleanest example of laser cooling. It has the same physics as the molasses case, with the second beam being replaced in a sense by a ficticious force. Note that in the two-beam molasses case, there are more complications, since one should really consider interference effects.

Energy conservation in laser cooling

Kinetic energy conservation

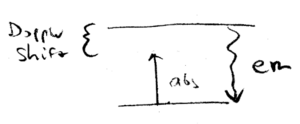
Where does the lost kinetic energy go, in cooling the atoms? In the beam cooling scenario, for example, you have moved a large number of atoms from high velocities to low velocities. How can this be reconciled with energy conservation? Well, there are only several possibilities for where the energy can go. In particular, there is light scattered by the atoms, and the energy is radiated away by spontaneous emission, as we shall now see.

Absorption is responsible for momentum change, and emission is responsible for energy conservation. Light emitted by the atom is at the resonant energy $\omega _{0}$, but can be absorbed when the photon is just slightly less than $\omega _{0}$. The emission is isotropic, whereas the incident light is directed and Doppler shift dependent.

Doppler cooling can be explained in this picture. Incident laser light is detuned below $\omega _{0}$ ("red detuned"), whereas emitted photons are, on average, at a higher frequency, so more energy is emitted than is absorbed, when an atom is cooled.

Energy conservation in general cooling schemes

The same intuition can be applied to all cooling schemes, including those used to cool solids and liquids. Phonon assisted absorption is balanced against emission, resulting in cooling:

How hard is it to cool liquids and solids? Consider a system at $T=1$K; that gives the phonon energy. Then $\hbar \omega =25,000$ Kelvin. In practice, there is a lower than unity fluorescence quantum yield, because there are non-radiative ways to exit the excited state. The cooling will be efficient, however, only when the quantum yield is higher than $1-1/25000$, which is typically unrealistic. Cooling with laser light is therefore not typically practical, for systems other than atoms, which have a unity fluorescence quantum yield. Molecules are hard, because they have non-radiative de-excitation pathways.