Magnetic resonance of a classical magnetic moment

Magnetic Resonance: The Classical Magnetic Moment in a Spatially Uniform Field

Harmonic oscillator versus two-level systems

Now, unlike in classical mechanics, most resonances studied in atomic physics are not harmonic oscillators, but two-level systems. Unlike harmonic oscillators, two-level systems show saturation. When a harmonic oscillator is driven longer or faster, higher and higher excited states are populated: the oscillator amplitude can become arbitrarily large. In contrast, the amplitude of oscillation in a two-level system is limited to one half in the appropriate dimensionless units.\footnote{An analogous dimensionless amplitude for the harmonic oscillator would be the amplitude measured in units of the oscillator ground state size.} Why, and under what conditions, do classical harmonic oscillator models of a two-level system work? A two-level system of energy difference Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} can be approximated by a harmonic oscillator of frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_o=E/\hbar} when saturation effects in the two-level system are negligible, i.e. when the population of the second excited state in the harmonic oscillator problem is negligible, or equivalently when the population ratio of the first excited state to the the ground state is small: $P_{1}/P_{0}\ll 1$. This is the basis for the classical Lorentz model of the electron bound in the atom that describes many linear atomic properties (for instance the refractive index) very well. See "The origin of the refractive index" in chapter 31 of the Feynman Lectures on Physics \cite{Feynman1963}. When saturation comes into play, i.e. when the initial ground state is appreciably depleted, the harmonic oscillator ceases to be a good model. The limit on the oscillation amplitude in a two-level system suggests that a classical system with periodic evolution and a limit on the amplitude, namely rotation, could provide a better classical model of a two-level system. Indeed, the motion of a classical magnetic moment in a uniform field provides a model that captures almost all features of the quantum-mechanical two-level system, the exception being the projection onto one of the two possible outcomes in a measurement.

Magnetic Moment in a Static Field

The interaction energy of a magnetic moment ${\bf {\mu }}$ with a magnetic field ${\bf {B}}$ is given by

$W=-{\bf {\mu }}\cdot {\bf {B}}$

In a uniform field the force

${\bf {F}}=-{\bf {\nabla }}W=0$

vanishes, but the torque

${\bf {T}}={\bf {\mu }}\times {\bf {B}}$

does not. For an angular momentum ${\bf {L}}$ the equation of motion is then

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{ {\bf{L}} } = {\bf{T}} = {\bf{\mu}} \times {\bf{B}} =\gamma {\bf{L}} \times {\bf{B}} }

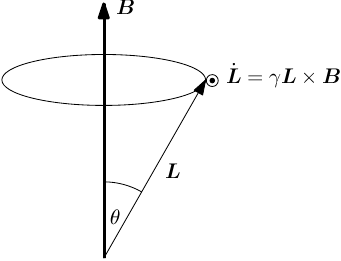
where we have introduced the gyromagnetic ratio Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} as the proportionality constant between angular momentum and magnetic moment, as shown in Figure \ref{fig:static_precession}.

{fig:static_precession} Precession of a the magnetic moment and associated angular momentum about a static field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} } .

This describes the precession of the magnetic moment about the magnetic field with angular frequency

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_L=-\gamma B }

$\Omega _{L}$ is known as the Larmor frequency. For electrons we have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_e=2\pi\times\unit{2.8}{\mega\hertz\per G}} , for protons Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_e=2\pi\times\unit{4.2}{\kilo\hertz\per G}} .

Transformation to a Rotating Coordinate System

A vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{A}} } rotating at constant angular velocity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{\Omega}} } is described by

${\dot {\bf {A}}}={\bf {\Omega }}\times {\bf {A}}$

Then the rates of change of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{A}} } measured in a coordinate system rotating at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{\Omega}} } and in an inertial system are related by

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{ {\bf{A}} }_\text{in} = \dot{ {\bf{A}} }_\text{rot} + {\bf{\Omega}} \times {\bf{A}} _\text{in} }

This follows immediately from the following facts:

• If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{A}} } is constant in the rotating system then ${\dot {\bf {A}}}_{\text{in}}={\bf {\Omega }}\times {\bf {A}}_{\text{in}}$.
• If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{\Omega}} =0} then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{ {\bf{A}} }_\text{in}=\dot{ {\bf{A}} }_\text{rot}} .
• Coordinate rotation is a linear transformation.

This transformation is sometimes abbreviated as the schematic rule

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{d}{dt}\right)_\text{rot}= \left(\frac{d}{dt}\right)_\text{in}- {\bf{\Omega}} \times\big(\big)_\text{in} }

It follows that the angular momentum in a rotating frame obeys

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{ {\bf{L}} }_\text{rot} = \dot{ {\bf{L}} }_\text{in}- {\bf{\Omega}} \times {\bf{L}} _\text{in} = {\bf{L}} \times(\gamma {\bf{B}} + {\bf{\Omega}} ) }

If we choose ${\bf {\Omega }}={\bf {\Omega _{L}}}=-\gamma {\bf {B}}$, then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{L}} _\text{rot}} is constant in the rotating frame. Often it is useful to think of a fictitious magnetic field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _\text{fict}= {\bf{\Omega}} /\gamma} that appears in a rotating frame.

Larmor's Theorem for a Charged Particle in a Magnetic Field

The vanishing of the torque on a magnetic moment when viewed in the correct rotating frame is reminiscent of Larmor's theorem for the motion of a charged particle in a magnetic field, which we now present.

According to answers.com, Lamor's theorem can be stated as For a system of charged particles, all having the same ratio of charge to mass, moving in a central field of force, the motion in a uniform magnetic induction B is, to first order in B, the same as a possible motion in the absence of B except for the superposition of a common precession of angular frequency equal to the Larmor frequency.

If the Lorentz force acts in an inertial frame,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{F}} _\text{in}=q {\bf{v}} _\text{in}\times {\bf{B}} }

then in the rotating frame, according to the rule \ref{eqn:rot_frame_transformation} we have

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{ {\bf{r}} }_\text{rot} &= \dot{ {\bf{r}} }_\text{in} - {\bf{\Omega}} \times {\bf{r}} _\text{in} \\ \ddot{ {\bf{r}} }_\text{rot} &= \ddot{ {\bf{r}} }_\text{in} - 2 {\bf{\Omega}} \times \dot{ {\bf{r}} }_\text{in} + {\bf{\Omega}} \times \left( {\bf{\Omega}} \times {\bf{r}} _\text{in} \right) \end{align}}

resulting in a force ${\bf {F}}_{\text{rot}}=m{\ddot {\bf {r}}}_{\text{rot}}$ in the rotating frame given by

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} {\bf{F}} _\text{rot} &= q {\bf{v}} _\text{in} \times {\bf{B}} - 2 m {\bf{\Omega}} \times {\bf{v}} _\text{in} + m {\bf{\Omega}} \times \left( {\bf{\Omega}} \times {\bf{r}} _\text{in} \right) \\ &= q {\bf{v}} _\text{in} \times \left( {\bf{B}} + 2 \frac{m}{q} {\bf{\Omega}} \right) + m {\bf{\Omega}} \times \left( {\bf{\Omega}} \times {\bf{r}} _\text{in} \right) \end{align}}

where we have used Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\ddot{r}_\text{in}= {\bf{F}} _\text{in}=q {\bf{v}} _\text{in}\times {\bf{B}} } . Choosing

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\frac{m}{q} {\bf{\Omega}} =- {\bf{B}} =-B {\bf{\hat e}} _z }

yields

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{F}} _\text{rot} =\frac{q^2}{4m}B^2 {\bf{\hat e}} _z\times\left( {\bf{\hat e}} _z\times {\bf{r}} _\text{in}\right)\approx 0 }

if the $B$ field is not too large. Thus the Lorentz force approximately disappears in the rotating frame.

Although Larmor's theorem is suggestive of the rotating co-ordinate transformation, it is important to realize that the two transformations, though identical in form, apply to fundamentally different systems. A magnetic moment is not necessarily charged- for example a neutral atom can have a net magnetic moment, and the neutron possesses a magnetic moment in spite of being neutral - and it experiences no net force in a uniform magnetic field. Furthermore, the rotating co-ordinate transformation is exact for a magnetic moment, whereas Larmor's theorem for the motion of a charged particle is only valid when the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^2 } term is neglected.

Note: A breakdown of Larmor's theorem occurs for free electrons. Free electrons orbit in a magnetic field at the cyclotron frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_c=qB/m} which is twice Larmor's frequency. The reason is that the orbiting velocity is now given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=\omega_c r } . As can be seen in the equation above, in this case, the centrifugal force equals minus one half of the Coriolis force, and therefore twice the frequency of the rotating frame is needed to cancel the effects of the applied magnetic field.

Rotating Magnetic Field on Resonance

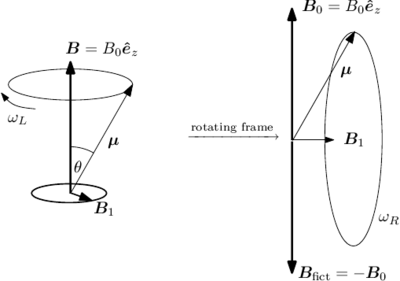
{fig:rotating_frame} Field and moment vectors in the static and rotating frames for the case of resonant drive.

Consider a magnetic moment Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{\mu}} } precessing about a field ${\bf {B}}=B_{0}{\bf {\hat {e}}}_{z}$ with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{\mu}} =(\mu, \theta, \phi=-\omega_0 t)} in spherical coordinates, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0=-\gamma B_0} . Assume that we now apply an additional field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _1} , in the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy} -plane rotating at $\omega _{0}$. To solve the resulting problem it is simplest to go into the rotating frame (Figure \ref{fig:rotating_frame}). Then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _1} is stationary, say along ${\bf {\hat {e}}}_{x}$, and there is an additional fictitious field ${\bf {B}}_{\text{fict}}={\bf {\omega _{0}}}/\gamma =-{\bf {B}}_{0}$ which cancels the field ${\bf {B}}_{0}$. So in the rotating frame we are left just with the static field ${\bf {B}}_{1}$, and the magnetic moment precesses about ${\bf {B}}_{1}$ at the Rabi frequency

$\omega _{R}=\gamma B_{1}$

A magnetic moment initially along the $-{\bf {\hat {e}}}_{z}$ axis will point along the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle + {\bf{\hat e}} _z} axis at a time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_r T=\pi} , while a magnetic moment parallel or antiparallel to the applied magnetic field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _1} does not precess in the rotating frame.

Question: {q:rabi_freq_blue_detuned} Assume the magnetic moment is initially pointing along the $-{\bf {\hat {e}}}_{z}$ axis. Assume that a rotating field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1\ll B_0} is applied, but that it rotates at a frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_1>\omega_0} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0} is the Larmor frequency for the static field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} =B_0 {\bf{\hat e}} _z} . Compared to the on-resonant case, $\omega _{1}=\omega _{0}$, is the oscillation frequency of the magnetic moment.

• larger
• the same
• smaller

Question: Same question as \ref{q:rabi_freq_blue_detuned} but for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_1<\omega_0} .

Rotating Magnetic Field Off-Resonance

If the rotation frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _1} does not equal the Larmor frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0=\gamma B_0} associated with the static field ${\bf {B}}_{0}$, then in the frame rotating with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _1} at frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} the static field is not completely cancelled by the fictitious field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega/\gamma} , but a difference along Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{\hat e}} _z} remains, giving rise to a total effective field in the rotating frame

${\bf {B}}_{\text{eff}}=B_{1}{\bf {\hat {e}}}_{x}+\left(B_{0}-{\frac {\omega }{\gamma }}\right){\bf {\hat {e}}}_{z}$

The effective field is static, lies at an angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} with the z

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan\theta=\frac{B_1}{B_0-\frac{\omega}{\gamma}} }

and is of magnitude

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| B_\text{eff}\right| =\sqrt{B_1^2+\left(B_0-\frac{\omega}{\gamma}\right)^2} }

The magnetic moment precesses around it with an effective (sometimes called generalized) Rabi frequency

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_R =\gamma B_\text{eff} =\sqrt{(\omega_0-\omega)^2+\omega_R^2}=\sqrt{\omega_R^2+\delta^2} }

where $\omega _{R}=\gamma B_{1}$ is the Rabi frequency associated with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta=\omega-\omega_0} is the detuning from resonance with the Larmor frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0=\gamma B_0} .

Geometrical Solution for the Classical Magnetic Moment in Static and Rotating Fields

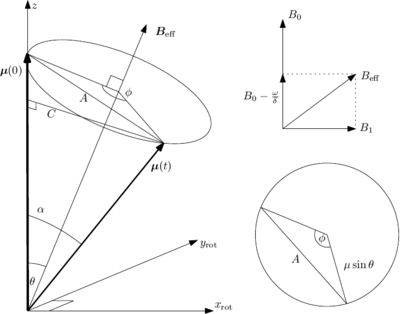
{fig:rotating_coord_construction} Geometrical relations for the spin in combined static and rotating magnetic fields, viewed in the frame co-rotating with the drive field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _1} . At lower right is a view looking straight down the ${\bf {B}}_{\text{eff}}$ axis.

Referring to Figure \ref{fig:rotating_coord_construction}, we have

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \phi &= \Omega_R t \\ C &= \mu \sin \alpha \\ A^2 &= \mu^2 ( 1 - \cos \alpha )^2 + C^2 \\ &= \mu^2 ( 1 - 2 \cos \alpha + \cos^2 \alpha + \sin^2 \alpha ) \\ &= 2 \mu^2 (1 - \cos \alpha ) \\ \Rightarrow \cos \alpha &= 1 - \frac{A^2}{2 \mu^2} \end{align}}

On the other hand

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{A}{2} &= \mu \sin \theta \sin \frac{\phi}{2} \\ A &= 2 \mu \sin \theta \sin \frac{\Omega_R t}{2} \end{align}}

so that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \cos \alpha &= 1 - \frac{4 \mu^2 \sin^2 \theta \sin^2 \frac{\Omega_R t}{2}}{2 \mu^2} \\ &= 1 - 2 \sin^2 \theta \sin^2 \frac{\Omega_R t}{2} \\ \mu_z(t) &= \mu \cos \alpha \\ &= \mu \left( 1 - 2 \frac{\omega_R^2}{\delta^2 + \omega_R^2} \sin^2 \frac{\Omega_R t}{2} \right) \\ \mu_z(t) &= \mu \left( 1 - 2 \frac{\omega_R^2}{\Omega_R^2} \sin^2 \frac{\Omega_R t}{2} \right) \end{align}}

With Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0 = \gamma B_0} the Larmor frequency of the static field, $\delta =\omega -\omega _{0}$ the detuning, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_R=\gamma B_1} the resonant and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_R=\sqrt{\omega_R^2+\delta^2}} the generalized Rabi frequencies. Note that the precession is faster, but the amplitude smaller for an off-resonant field than for the resonant case. The above result is also the correct quantum-mechanical result.

If we define the quantity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P= \frac{\mu_z(t)-\mu_z(0)}{2\mu_z(0)} } , we obtain

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P= \frac{\omega_R^2}{\Omega_R^2} \sin^2 \frac{\Omega_R t}{2} }

In the quantum mechanical treatment, $P$ is the probability to find the system in the second state, or the spin flip probability.

"Rapid" Adiabiatic Passage

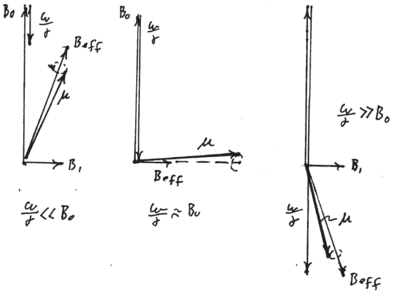
Rapid adiabatic passage is a technique for inverting a spin by (slowly) sweeping the detuning of a drive field through resonance. "Slowly" means slowly compared to the Larmor frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma B_\text{eff}} about the effective static field in the rotating frame for all times. The physical picture is as follows. Assume the detuning is initially negative (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta<0} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| \delta\gg\omega_R\right| } ). Since

$\tan \theta ={\frac {B_{1}}{B_{0}-{\frac {\omega }{\gamma }}}}={\frac {\omega _{R}}{\omega _{0}-\omega }}=-{\frac {\omega _{R}}{\delta }}$

the effective magnetic field initially points of a small angle relative to the ${\bf {\hat {e}}}_{z}$ axis. If the detuning is increased slowly compared to the Larmor frequency, the spin will continue to precess tightly around ${\bf {B}}_{\text{eff}}$, which for $\delta =0$ points along the x axis, and for $\delta \gg \omega _{R}$ along the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - {\bf{\hat e}} _z} axis (see Figure \ref{fig:rapid_adiabatic_passage}).

{fig:rapid_adiabatic_passage} {Motion of the spin during rapid adiabatic passage, viewed in the frame rotating with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _1} . The spin's rapid precession locks it to the direction of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _\text{eff}} and thus it is dragged through an angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} as the frequency is swept through resonance.

Thus the magnetic moment, starting out along ${\bf {B}}_{0}=B_{0}{\bf {\hat {e}}}_{z}$, ends up pointing along Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - {\bf{B}} _0=B_0 {\bf{\hat e}} _z} . Note that in the rotating frame Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{\mu}} } remains always (almost) parallel to the effective field Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _\text{eff}} . A similar precess is used in magnetic traps for atoms, but there Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{B}} _\text{eff}} is a real, spatially dependent field constant in time. As the atom moves in this field, the fast precession of the magnetic moment about the local field keeps its direction locked to the local field, whose direction varies in the lab frame. Returning to rapid adiabatic passage, since the generalized Rabi frequency is smallest and equal to the resonant Rabi frequency $\omega _{R}$ at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta=0} , the adiabatic requirement is most severe there, i.e. near Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\pi/2} . Near Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\pi/2} we have, with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_z=B_0-1/\gamma\omega(t)} ,

$\left|{\dot {\theta }}\right|={\frac {\left|{\dot {B}}_{z}\right|}{B_{1}}}={\frac {\left|{\dot {\omega }}\right|}{\gamma B_{1}}}={\frac {\left|{\dot {\omega }}\right|}{\omega _{R}}}{\overset {!}{\ll }}\omega _{R}$

where the exclamation point in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{!}{\ll}} indicates a requirement which we impose. Consequently, if the evolution is to be adiabatic, we must have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| \dot{\omega}\right| \ll\omega_R^2} . This means that the change Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\omega} of rotation frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} per Rabi period $T=2\pi /\omega _{R}$, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| \Delta\omega\right| = \left| \dot\omega\right| T= \left| \dot\omega\right| /\omega_R 2\pi} , must be small compared to the Rabi frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_R} . The quantum mechanical treatment yields a probability for non-adiabatic transition (probability for the magnetic moment not following the magnetic field) given by

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_\text{na}=exp\left(-\frac{\pi}{2}\frac{\omega^2_R}{ \left| \dot\omega\right| }\right) }

in agreement with the above qualitative discussion.