Steady-state solutions
The optical Bloch equations provide a time-dependent quantum
description of a spontaneously emitting atom driven by a classical
electromagnetic field. Considerable insight into the physical
processes involved can be gained by studying these equations in the
transient excitation limit, as well as the steady-state limit, as we
see in this section. We begin by considering the coherent part of the
evolution, then extend this to re-visit the Bloch sphere picture of
the optical Bloch equations, which provides useful visualizations of
transient responses and steady state solutions.
Eigenstates of the Jaynes-Cummings Hamiltonian
The optical Bloch equations are
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604d2158dbbebf16674738f973827dbb18e3a819)
where the Hamiltonian is

Useful limits to this equation of motion can be obtained, for example,
by solving for  in the steady state, when
in the steady state, when  . Both
the Hamiltonian part of this equation, and the damping part, are
important to consider, and we begin here by reviewing the coherent
evolution under
. Both
the Hamiltonian part of this equation, and the damping part, are
important to consider, and we begin here by reviewing the coherent
evolution under  .
.
 arises from the Jaynes-Cummings interaction we have previously
considered in the context of cavity QED, describing a single two-level
atom interacting with a single mode of the electromagnetic field:
arises from the Jaynes-Cummings interaction we have previously
considered in the context of cavity QED, describing a single two-level
atom interacting with a single mode of the electromagnetic field:
![{\displaystyle H_{JC}={\frac {\hbar \omega _{0}}{2}}\left[{|e\rangle \langle e|-|g\rangle \langle g|}\right]+\hbar \omega a^{\dagger }a+{\frac {\hbar \Omega }{2}}\left[{|g\rangle \langle e|+|e\rangle \langle g|}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/630609e3aab033690555f530c6e4323ba84a5538)
The last term in this expression is  , the dipole interaction
between atom and field. By defining
, the dipole interaction
between atom and field. By defining  and
and
 , we may write this interaction as
, we may write this interaction as
![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{\sigma _{+}+\sigma _{-}}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3410ceeb8ffe707f367fc599209a8dad817b08df)
In the frame of reference of the atom and field, recall that

When near resonance,  , and because the
, and because the
 and
and  terms oscillate at nearly twice the frequency
of
terms oscillate at nearly twice the frequency
of  , those terms can be dropped. Doing so is known as the
rotating wave approximation, and it gives us a simplified
interaaction Hamiltonian
, those terms can be dropped. Doing so is known as the
rotating wave approximation, and it gives us a simplified
interaaction Hamiltonian
![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{a^{\dagger }\sigma _{+}+a\sigma _{-}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/508bc170a806987fec962bd6efde10f42f6acb93)
Under this approximation, it is useful to note that this interaction
merely exchanges one quantum of excitation from atom to field, and
back, so that the total number of excitations  is a constant of the motion. We may thus write the total Hamiltonian,
in the rotating wave approximation, as
is a constant of the motion. We may thus write the total Hamiltonian,
in the rotating wave approximation, as

where we have defined  , and
, and  . Below, we may use
. Below, we may use  to simplify
writing.
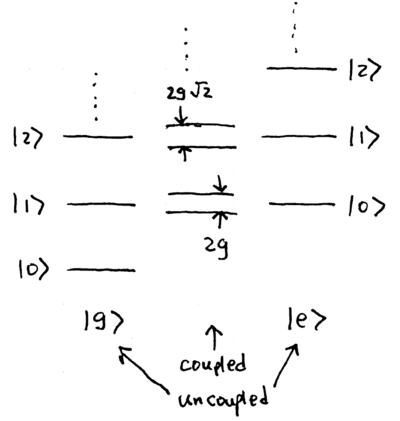
What are the eigenstates of this Hamiltonian? It describes a
two-level system coupled to a simple harmonic oscillator; when
uncoupled, if
to simplify
writing.
What are the eigenstates of this Hamiltonian? It describes a
two-level system coupled to a simple harmonic oscillator; when
uncoupled, if  , then the eigenstates are simply those of
, then the eigenstates are simply those of
 ,
,  and
and  , as shown here:
, as shown here:
\noindent
When coupled, degenerate energy levels split, with harmonic oscillator
levels  and
and  splitting into two energy levels separated
by
splitting into two energy levels separated
by  . Since the coupling only pairs levels separated by
one quantum of excitation, it is straightforward to show that the
eigenstates of the Jaynes-Cummings Hamiltonian fall into well defined
pairs of states, which we may label as
. Since the coupling only pairs levels separated by
one quantum of excitation, it is straightforward to show that the
eigenstates of the Jaynes-Cummings Hamiltonian fall into well defined
pairs of states, which we may label as  ; these are
; these are
![{\displaystyle |\pm ,n\rangle ={\frac {1}{\sqrt {2}}}\left[{|e,n\rangle \pm |g,n+1\rangle }\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55f08b48a6a98c378c7ba35aff03487dd1c3463e)
and they have energies

When  , similar physics result, but with slightly more
complicated expressions describing the eigenstates, as we shall see
when we later return to the "dressed states" picture.
, similar physics result, but with slightly more
complicated expressions describing the eigenstates, as we shall see
when we later return to the "dressed states" picture.
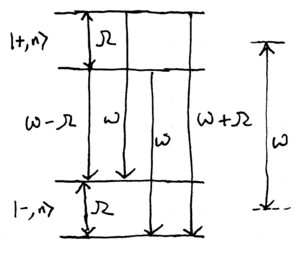
Strongly driven atom: Mollow triplet
An atom strongly coupled to a single mode electromagnetic field, or an
atom driven strongly by a single mode field, will thus have an
emission spectrum described by the coupled energy level diagram:
\noindent
where, to good approximation, the energy level differences are
 and
and  . These three lines which appear in the
spectrum are known as the Mollow triplet:
. These three lines which appear in the
spectrum are known as the Mollow triplet:
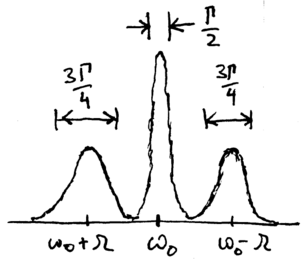
The Mollow triplet is experimentally observed in a wide variety of
systems. However, while our energy eigenstate analysis has predicted
the number and frequencies of the emission lines, it fails to explain
a key characteristic: the widths are not the same. If the central
peak at  has width
has width  , the two sidebands each have a
width of
, the two sidebands each have a
width of  . To explain this, we need the optical Bloch
equations.
. To explain this, we need the optical Bloch
equations.
Rotating frame of reference for atom + field
A simplification worth using in the study of the optical Bloch
equations is a transformation into the rotating frame of the light
field. The Hamiltonian for the atom + classical field may be written
in general as

where  parameterizes the strength field,
parameterizes the strength field,  is the atomic
transition frequency, and
is the atomic
transition frequency, and  are the Pauli matrices as usual.
Define
are the Pauli matrices as usual.
Define  , such that the
Schr\"odinger equation
, such that the
Schr\"odinger equation

can be re-expressed as
![{\displaystyle i\partial _{t}|\phi (t){\rangle }=\left[{e^{i\omega Zt/2}He^{-i\omega Zt/2}-{\frac {\omega }{2}}Z}\right]|\phi (t){\rangle }\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd25a9fb634a32a02f90b6e2ac20fee9739e5132)
Since

Eq.(\ref{eq:nmr:schrB}) simplifies to become
![{\displaystyle i\partial _{t}|\phi (t){\rangle }=\left[{{\frac {\omega _{0}-\omega }{2}}Z+gX}\right]|\phi (t){\rangle }\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d261013cb7bed576b4fc74be31542e84d10c527b)
where the terms on the right multiplying the state can be identified as the
effective `rotating frame' Hamiltonian. The solution to this equation is
![{\displaystyle |\phi (t)\rangle =e^{i\left[{{\frac {\omega _{0}-\omega }{2}}Z+gX}\right]t}|\phi (0){\rangle }\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98d107b245ae95facc20ec4573b03e27b7a613b5)
The concept of resonance arises from the behavior of this time
evolution, which can be understood as being a single qubit rotation
about the axis

by an angle

When  is far from
is far from  , the qubit is negligibly affected
by the laser field; the axis of its rotation is nearly parallel with
, the qubit is negligibly affected
by the laser field; the axis of its rotation is nearly parallel with
 , and its time evolution is nearly exactly that of the free
atom Hamiltonian. On the other hand, when
, and its time evolution is nearly exactly that of the free
atom Hamiltonian. On the other hand, when  ,
the free atom contribution becomes negligible, and a small laser field
can cause large changes in the state, corresponding to rotations about
the
,
the free atom contribution becomes negligible, and a small laser field
can cause large changes in the state, corresponding to rotations about
the  axis. The enormous effect a small field can have on the
atom, when tuned to the appropriate frequency, is responsible for the
concept of atomic `resonance,' as well as nuclear magnetic resonance.
axis. The enormous effect a small field can have on the
atom, when tuned to the appropriate frequency, is responsible for the
concept of atomic `resonance,' as well as nuclear magnetic resonance.
Bloch vector evolution
We have previously seen that an arbitrary qubit state  can be represented as being a
point on a unit sphere, located at
can be represented as being a
point on a unit sphere, located at  in polar
coordinates. Similarly, a density matrix
in polar
coordinates. Similarly, a density matrix  may be depicted as
being a point inside or on the unit sphere, using
may be depicted as
being a point inside or on the unit sphere, using

where  is the Bloch vector representation of
is the Bloch vector representation of  .
Explicitly, if we let
.
Explicitly, if we let
![{\displaystyle \rho =\left[{\begin{array}{cc}{\rho _{ee}}&{\rho _{eg}}\\{\rho _{ge}}&{\rho _{gg}}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/614be7a08a95774b74f988c678248fd3055558a9)
then

Visulization of the evolution of a density matrix under the optical
Bloch equations is thus helped by rewriting them in terms of a
differential equation for  . A convenient starting point for
this is the optical Bloch equation
. A convenient starting point for
this is the optical Bloch equation
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604d2158dbbebf16674738f973827dbb18e3a819)
using the rotating frame Hamiltonian (suppressing  )
)

This gives us the equations of motion

Note how these equations of motion provide a simple set of flows on
the Bloch sphere: the  terms correspond to a rotation in the
terms correspond to a rotation in the
 plane,
plane,  corresponds to a rotation in the
corresponds to a rotation in the
 plane, and
plane, and  drives a relaxation process
which shrinks
drives a relaxation process
which shrinks  and
and  components of the Bloch vector,
while moving the
components of the Bloch vector,
while moving the  component toward
component toward  .
Physically, what is the meaning of
.
Physically, what is the meaning of  ,
,  , and
, and  ?
?  is
manifestly the population difference between the excited and ground
states. The other two components may be interpreted by recognizing
that the average dipole moment of the atom is
is
manifestly the population difference between the excited and ground
states. The other two components may be interpreted by recognizing
that the average dipole moment of the atom is

Thus,  and
and  correspond to the phase components of the atomic
dipole moment which are in-phase and in quadrature with the incident
electromagnetic field.
correspond to the phase components of the atomic
dipole moment which are in-phase and in quadrature with the incident
electromagnetic field.
Transient repsonse of the optical Bloch equations
The optical Bloch equations allow us to study the internal state of
the atom as it changes due to the external driving field, and due to
spontaneous emission.
Starting from the time-independent form of the equations,

we may note that when  and at resonance,
and at resonance,  ,
the Bloch vector exhibits pure damping behavior, towards
,
the Bloch vector exhibits pure damping behavior, towards  , and
, and
 .
When
.
When  , Rabi oscillations occur, represnted by rapid
rotations of the Bloch vector about
, Rabi oscillations occur, represnted by rapid
rotations of the Bloch vector about  . Since the relaxation
along
. Since the relaxation
along  occurs at rate
occurs at rate  , and the relaxation about
, and the relaxation about
 occurs at rate
occurs at rate  , we might expect that the average
relaxation rate of the rotating components under such a strong driving
field would be
, we might expect that the average
relaxation rate of the rotating components under such a strong driving
field would be  . The remaining
component
. The remaining
component  does not rotate, because it sits along
does not rotate, because it sits along  , the
axis of rotation. Thus, it relaxes with rate
, the
axis of rotation. Thus, it relaxes with rate  . Computation
of the eigenvalues of the equations of motion verify this qualitative
picture, and show that for
. Computation
of the eigenvalues of the equations of motion verify this qualitative
picture, and show that for  , and
, and  , the
eigenvalues of motion are
, the
eigenvalues of motion are  and
and  . These
correspond to a main peak at
. These
correspond to a main peak at  with width
with width  , and two
sidebands at
, and two
sidebands at  , with widths
, with widths  , thus
explaining the widths of the observed Mollow triplet lines.
, thus
explaining the widths of the observed Mollow triplet lines.
Steady-state solution of the optical Bloch equations
The steady state solution of the optical Bloch equations are found by
setting all the time derivatives to zero, giving a set of three
simultaneous equations,

The solutions are (up to overall minus signs which can be absorbed
into definitions):

Physically, these are Lorentzians; the  solution (the component
in quadrature with the dipole) corresponds to an absorption curve with
half-width
solution (the component
in quadrature with the dipole) corresponds to an absorption curve with
half-width

and the  solution (the component in-phase with the dipole)
corresponds to a dispersion curve. And under a strong driving field,
as
solution (the component in-phase with the dipole)
corresponds to a dispersion curve. And under a strong driving field,
as  ,
,  , indicating that the
populations in the excited and ground states are equalizing. The
steady-state population in the excited state is
, indicating that the
populations in the excited and ground states are equalizing. The
steady-state population in the excited state is

an important result that will later be used in studying light forces.
These solutions can be re-expressed in a simplified manner by defining
the saturation parameter

in terms of which we find

As  , the atomic transitions become {\em
saturated}, and the linewidth of the transition broadens from its
natural value
, the atomic transitions become {\em
saturated}, and the linewidth of the transition broadens from its
natural value  , becoming
, becoming  on
resonance, at
on
resonance, at  .
.
References
![{\displaystyle {\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604d2158dbbebf16674738f973827dbb18e3a819)




![{\displaystyle H_{JC}={\frac {\hbar \omega _{0}}{2}}\left[{|e\rangle \langle e|-|g\rangle \langle g|}\right]+\hbar \omega a^{\dagger }a+{\frac {\hbar \Omega }{2}}\left[{|g\rangle \langle e|+|e\rangle \langle g|}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/630609e3aab033690555f530c6e4323ba84a5538)



![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{\sigma _{+}+\sigma _{-}}\right]\left[{a+a^{\dagger }}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3410ceeb8ffe707f367fc599209a8dad817b08df)





![{\displaystyle H_{I}={\frac {\hbar \Omega }{2}}\left[{a^{\dagger }\sigma _{+}+a\sigma _{-}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/508bc170a806987fec962bd6efde10f42f6acb93)












![{\displaystyle |\pm ,n\rangle ={\frac {1}{\sqrt {2}}}\left[{|e,n\rangle \pm |g,n+1\rangle }\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55f08b48a6a98c378c7ba35aff03487dd1c3463e)











![{\displaystyle i\partial _{t}|\phi (t){\rangle }=\left[{e^{i\omega Zt/2}He^{-i\omega Zt/2}-{\frac {\omega }{2}}Z}\right]|\phi (t){\rangle }\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd25a9fb634a32a02f90b6e2ac20fee9739e5132)

![{\displaystyle i\partial _{t}|\phi (t){\rangle }=\left[{{\frac {\omega _{0}-\omega }{2}}Z+gX}\right]|\phi (t){\rangle }\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d261013cb7bed576b4fc74be31542e84d10c527b)
![{\displaystyle |\phi (t)\rangle =e^{i\left[{{\frac {\omega _{0}-\omega }{2}}Z+gX}\right]t}|\phi (0){\rangle }\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98d107b245ae95facc20ec4573b03e27b7a613b5)









![{\displaystyle \rho =\left[{\begin{array}{cc}{\rho _{ee}}&{\rho _{eg}}\\{\rho _{ge}}&{\rho _{gg}}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/614be7a08a95774b74f988c678248fd3055558a9)






























