Interferometry and metrology

Interferometry and metrology

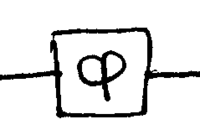
Suppose you are given a phase shifter of unknown $\phi$:

\noindent How accurately can you determine $\phi$, given a certain time, and laser power? In this section, we consider this basic measurement problem, and show how the usual shot noise limit can be exceeded by using quantum states of light, reaching a quantum limit determined by Heisenberg's uncertainty principle. This limit is achieved using entanglement, which can be realized using entangled multi-mode photons, or by a variety of squeezed states. The physics behind such quantum measurement techniques generalizes to a wide range of metrology problems, but a common challenge the need to reduce loss.

Shot noise limit

{{#lst:Interferometer shot noise limit|content}}

Heisenberg limit: entanglement

The shot noise limit we have just seen, however, is not fundamental. Here is a simple argument that something better should be possible. Recall that the desired signal at the output of our Mach-Zehnder interferometer is $X=a^{\dagger }a-b^{\dagger }b$, and the noise is $Y=a^{\dagger }b+b^{\dagger }a$. If the inputs have $a^{\dagger }a=n$ and $b^{\dagger }b=0$, and if $Y$ were zero, then the measured signal would be $n\cos \phi$. And at the balanced operating point $\phi =\pi /2$,

${\frac {|\Delta m|}{\Delta \phi }}=n\sin \phi \leq n\,.$

Thus, if the smallest photon number change resolvable is $\Delta m=1$, then $n\Delta \phi \geq 1$, from which it follows that

$\Delta \phi \geq {\frac {1}{n}}\,.$

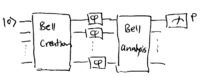
This is known as the "Heisenberg limit" on interferometry. There are some general proofs in the literature that such a limit is the best possible on interferometry. It governs more than just measurements of phase shifters; gyroscopes, mass measurements, and displacement measurements all use interferometers, and obey a Heisenberg limit. The argument above only outlines a sketch for why $1/n$ might be an achievable limt, versus $1/{\sqrt {n}}$; it assumes that the noise $Y$ can be made zero, however, and does not provide a means for accomplishing this in practice. Many ways to reach the Heisenberg limit in interferometry are now known. Given the basic structure of a Mach-Zehnder interferometer,

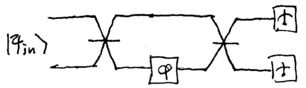
\noindent one can consider changing the input state $|\psi _{in}{\rangle }$, changing the beamsplitters, or changing the measurement. Common to all of these approaches is the use of entangled states. How entanglement makes Heisenber-limited interferometry possible can be demonstrated by the following setup. Let us replace the beamsplitters in the Mach-Zehnder interferometer with entangling and dis-entangling devices:

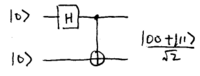
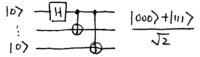
\noindent Conceptually, the unusual beamsplitters may be the nonlinear Mach-Zehnder interferometers we discussed in Section~2.3. They may also be described by simple quantum circuits, using the Hadamard and controlled-{\sc not} gate; for two qubits, the circuit is

\noindent Note how the output is one of the Bell states. For three qubits, the circuit is

\noindent This output state, $|000{\rangle }+|111{\rangle }$ (suppressing normalization) is known as a GHZ (Greenberger-Horne-Zeilinger) state. Straightforward generalization leads to larger "Schrodinger cat" states $|00\cdots 0{\rangle }+|11\cdots 1{\rangle }$, using one Hadamard gate and $n$ controlled-{\sc not} gates. Note that the reversed circuit unentangles the cat states to produce computational basis states. The important feature of such $n$-qubit cat states, for our purpose, is how they are transformed by phase shifters. A single qubit $|0{\rangle }+|1{\rangle }$ becomes $|0{\rangle }+e^{i\phi }|1{\rangle }$. Similarly, two entangled qubits in the state $|00{\rangle }+|11{\rangle }$, when sent through two phase shifters, becomes $|00{\rangle }+e^{2i\phi }|11{\rangle }$, since the phases add. And $n$ qubits in the state $|00\cdots 0{\rangle }+|11\cdots 1{\rangle }$ sent through $n$ phase shifters becomes $|00\cdots 0{\rangle }+e^{ni\phi }|11\cdots 1{\rangle }$. When such a phase shifted state is un-entangled, using the reverse of the entangling circuit, the $n$ controlled-{\sc not} gates leave the state $|00\cdots 0{\rangle }[|0\rangle +e^{ni\phi }|1\rangle ]$, where the last $n-1$ qubits are left in $|0{\rangle }$, and the first qubit (the qubit used as the control for the {\sc cnot} gates) is

${\frac {|0\rangle +e^{ni\phi }|1{\rangle }}{\sqrt {2}}}\,.$

Compare this state with that obtained from the single qubit interferometer, Eq.(\ref{eq:l7-1qubitphase}); instead of a phase $\phi$, the qubit now carries the phase $n\phi$. This means that the probability $P$ of measuring a single photon at the output becomes

$P={\frac {1+\cos(n\phi )}{2}}\,.$

The standard deviation, from repeating this experiment, on average, would be

$\Delta P={\sqrt {P(1-P)}}={\frac {\sin(n\phi )}{2}}\,.$

Using $dP/d\phi =-n\sin(n\phi )/2$, we obtain for the uncertainty in $\phi$,

$\Delta \phi ={\frac {\Delta \phi }{\left|{\frac {dP}{d\phi }}\right|}}={\frac {1}{n}}\,,$

which meets the Heisenberg limit.

Squeezed light interferometry

{{#lst:Squeezed light interferometry|content}}

Sensitivity to loss

Entangled states, while very useful for a wide variety of tasks, including interferometry and metrology, are unfortunately generally very fragile. In particular, entangled photon states degrade quickly with due to loss. Consider, for example, the two-qubit state $|00{\rangle }+|11{\rangle }$ (suppressing normalization). If one of theses photons goes through a mostly-transmitting beamsplitter, then the photon may be lost; let us say this happens with probability $\epsilon$. If a photon is lost, the state collapses into one with one remaining photon, say $|10{\rangle }$. This is a product state -- no longer entangled. It is not even a superposition. No photon is lost with probability $(1-\epsilon )$. Even worse, if both modes suffer potential loss of a photon, then no matter whcih mode looses a photon, the entangled state collapses; this happens even if just one photon is lost. Thus, the state retains some entanglement only with probability $(1-\epsilon )^{2}$. And worst of all, if we have an $n$-photon cat state $|00\cdots 0{\rangle }+|11\cdots 1{\rangle }$, and all modes are subject to loss $\epsilon$, then useful entanglement is retained only with probability $(1-\epsilon )^{n}$. Due to such loss, the phase measurement uncertainty of an entangled state interferometer will go as

${\langle }\Delta \phi \rangle \sim {\frac {1}{n(1-\epsilon )^{n}}}\,,$

which is clearly undesirable. Some physical systems, however, naturally suffer very little loss, and can keep entangled states intact for long times. Photons unfortunately do not have that feature, but certain atomic states, such as hyperfine transitions, can be very long lived. Thus, many of the concepts derived in the context of quantum states of light, actually turn out to be more useful when applied to quantum states of matter.