What is quantum about light -- is it the wave behavior of
electromagnetic waves? Or is it the particle behavior of photons?
The truth is much deeper than either, and much more interesting!
We begin with a brief review of the formalism of the simple harmonic
oscillator, used to model single modes of light. Light from
incandescent and other thermal sources can be described using this
model. But more important to us will be coherent light from lasers,
which is described by coherent states of light. These, and
other more quantum states of light can be usefully depicted using a
phase-space representation, as we demonstrate with  plots.
Plots of thermal, coherent, and photon number states illustrate
unique quantum properties which can lead to non-classical field
fluctuations and statistical properties, particularly at the level of
a single photon.
plots.
Plots of thermal, coherent, and photon number states illustrate
unique quantum properties which can lead to non-classical field
fluctuations and statistical properties, particularly at the level of
a single photon.
Starting point: electromagnetism
Recall that the energy of an electromagnetic field may be expressed as
the Hamiltonian
![{\displaystyle H={\frac {1}{2}}\int \,d^{3}r\left[{\epsilon _{0}|{\vec {E}}|^{2}+{\frac {1}{\mu _{0}}}|{\vec {B}}|^{2}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6757b1d12769ae5a06329ce08be318f4d060019)
where  and
and  are the electric and magnetic fields, and
are the electric and magnetic fields, and
 and
and  are the permitivity and permeability of free
space. Second quantization of this Hamiltonian led to a new
expression for this energy, in terms of quantum operators,
are the permitivity and permeability of free
space. Second quantization of this Hamiltonian led to a new
expression for this energy, in terms of quantum operators,

where

and the quantized electric field is
![{\displaystyle {\vec {E}}=i{\vec {e}}{\sqrt {\frac {\hbar \omega }{\epsilon _{0}V}}}\left[{ae^{i(kr-\omega t)}-a^{\dagger }e^{-i(kr-\omega t)}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b74b46b82cb4578fc67ec4b301250396178c7ec5)
where  is the polarization vector, and
is the polarization vector, and  is the
quantization volume.
The bottom line of the QED Hamiltonian is that we may model a single
mode of the electromagnetic field using this Hamiltonian:
is the
quantization volume.
The bottom line of the QED Hamiltonian is that we may model a single
mode of the electromagnetic field using this Hamiltonian:

This is the Hamiltonian of a simple harmonic oscillator. Everything
we are interested in about the quantum properties of light will come
from this Hamiltonian, and small perturbations of it!
Number and Thermal States
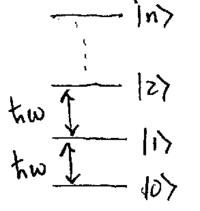
The simple harmonic oscillator Hamiltonian has eigenstates labeled
 , where
, where  , such that the energy levels
may be depicted as a ladder of equally spaced rungs starting at
, such that the energy levels
may be depicted as a ladder of equally spaced rungs starting at
 , as shown in this figure:
, as shown in this figure:
In terms of these energy eigenstates, known as number states,
the Hamiltonian can be written as  . Note
that the eigenstates are orthogonal:
. Note
that the eigenstates are orthogonal:  . The
state
. The
state  is said to be an
is said to be an  photon state.
The ladder operators acting on these energy eigenstates,
photon state.
The ladder operators acting on these energy eigenstates,  and
and
 , are known as the anihilation and creation operators,
respectively. They satisfy the following properties, which are well
worth remembering:
, are known as the anihilation and creation operators,
respectively. They satisfy the following properties, which are well
worth remembering:
![{\displaystyle {\begin{array}{rcl}a|n\rangle &=&{\sqrt {n}}|n-1{\rangle }\\a^{\dagger }|n\rangle &=&{\sqrt {n+1}}|n+1{\rangle }\\\,[a,a^{\dagger }]&=&1\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e69ce048473b86f8e3d8001a8805ee1a254f2c22)
A good way to reconstruct these is to remember just that  ,
and
,
and  .
Light produced by thermal emission sources, such as resistive
filaments, gas discharge, or other radiating black bodies, is a
statistical mixture of number states, known as a thermal state,
and sometimes called "chaotic light." This mixture is described by
a density matrix characterizing a Boltzman distribution of number
states,
.
Light produced by thermal emission sources, such as resistive
filaments, gas discharge, or other radiating black bodies, is a
statistical mixture of number states, known as a thermal state,
and sometimes called "chaotic light." This mixture is described by
a density matrix characterizing a Boltzman distribution of number
states,

where  ,
,  is Boltzmann's constant,
is Boltzmann's constant,  is
temperature, and
is
temperature, and

is the usual partition function normalization. This gives us

The mean number of photons in a thermal state is

If we define the probability distribution  by
by  , then
, then

This distribution, together with some mode volume considerations,
gives Planck's law of blackbody radiation.
Note that  , as expected for a properly normalized
probability distribution. A quick calculation gives
, as expected for a properly normalized
probability distribution. A quick calculation gives

and thus the variance is  . Constrast this with the Poisson distribution, for
which average and variance are the same. Laser light, as is well
known, has such a Poisson distribution of photon number; it is thus
quite distinct from thermal light, from the standpoint of number
statistics.
. Constrast this with the Poisson distribution, for
which average and variance are the same. Laser light, as is well
known, has such a Poisson distribution of photon number; it is thus
quite distinct from thermal light, from the standpoint of number
statistics.
Coherent States and the  Representation
Representation
Definition & properties. A coherent state  is
defined to be an eigenstate of the anihilation operator
is
defined to be an eigenstate of the anihilation operator  :
:

with normalization  . It is important to keep
in mind that
. It is important to keep
in mind that  is a complex number. In the number basis
is a complex number. In the number basis
 , a coherent state has the representation
, a coherent state has the representation

Let  . By definition,
. By definition,  is an eigenstate
of
is an eigenstate
of  , and thus
, and thus

This gives a recursion relation for  ; from this, and the
normalization of
; from this, and the
normalization of  , it follows that
, it follows that

In contrast to basis states usually used for Hilbert spaces, coherent
states are not orthogonal to each other:

However, coherent states are often still useful as an {\em
overcomplete} basis, taking advantage of this resolution of identity:

What physical state does the coherent state represent? The diagonal
elements of  have a Poisson distribution,
have a Poisson distribution,

It follows from this that the average photon number  . Similarly, the variance in the
photon number is
. Similarly, the variance in the
photon number is  . This is distinct from the thermal state
we studied above, and agrees with the well known Poisson statistics of
photon number for laser light. The coherent state represents a mode
of the electromagnetic field. For
. This is distinct from the thermal state
we studied above, and agrees with the well known Poisson statistics of
photon number for laser light. The coherent state represents a mode
of the electromagnetic field. For  ,
,
 is its amplitude, and
is its amplitude, and  its phase. In fact, we will
see that a coherent state provides an excellent quantum-mechanical
model of classical states of light.
its phase. In fact, we will
see that a coherent state provides an excellent quantum-mechanical
model of classical states of light.
Visualization: 
A good way to visualize this
coherent state (and other quantum states of light, as we shall see) is
in terms of something known as "quasi-probability" distributions.
Let us define

where  is the density matrix of the state which we wish to
visualize, and
is the density matrix of the state which we wish to
visualize, and  is a complex number, such that
is a complex number, such that
 may be represented by non-negative, real-valued
two-dimensional plot. Note that
may be represented by non-negative, real-valued
two-dimensional plot. Note that  is normalized:
is normalized:

independent of  . In this sense, we may interpret
. In this sense, we may interpret
 as a probability distribution.
as a probability distribution.
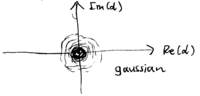
Vacuum state
For example, consider the  plot for
plot for  ,
the "vacuum" state. This is
,
the "vacuum" state. This is  , a gaussian centered at the origin in the
, a gaussian centered at the origin in the
 ,
,  plane:
plane:
Thermal state
Another example is provided by the thermal state  , for which
, for which

Inserting Eq.(\ref{eq:thermal_prob}) for  , we find
, we find

This again is a gaussian, centered at the origin:
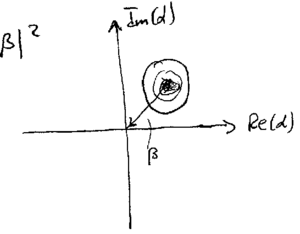
Coherent state
A third example is given by the coherent state itself; let  . The
. The  representation of this is
representation of this is

This is a gaussian centered at  :
:
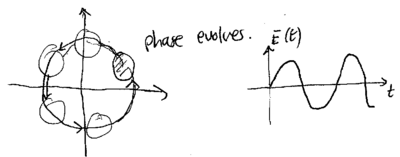
Recall that the Hamiltonian for a mode of light as it propagates is  . A coherent state thus evolves to become
. A coherent state thus evolves to become

In other words, a coherent state parameterized by  evolves
with time to become a coherent state parameterized by
evolves
with time to become a coherent state parameterized by  . In terms of the
. In terms of the  representation, this
means that the time evolution of a coherent state centered at some
initial point
representation, this
means that the time evolution of a coherent state centered at some
initial point  is depicted as rotation about the origin, as the
phase of its electric field evolves:
is depicted as rotation about the origin, as the
phase of its electric field evolves:
Note that this understanding allows us to visualize the thermal state
as being a mixture of coherent states with random phase.
Fluctuations and Noise
The  depiction of a state of light is particularly useful
because it allows direct visualization of the statistical properties
of quantum states versus the classical coherent states.
Recall that the Heisenberg uncertainty principle restricts the product
of fluctuations in two conjugate observables, such as position and
momentum:
depiction of a state of light is particularly useful
because it allows direct visualization of the statistical properties
of quantum states versus the classical coherent states.
Recall that the Heisenberg uncertainty principle restricts the product
of fluctuations in two conjugate observables, such as position and
momentum:

For a simple harmonic oscillator,

and using the fact that for a coherent state  ,
,
 , and
, and  , we find that
, we find that

These give

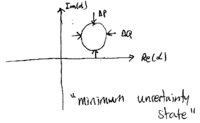
so that  . Thus, the coherent state is
a minimum uncertainty state of light. This distinction is
apparent from the width of the coherent state in the
. Thus, the coherent state is
a minimum uncertainty state of light. This distinction is
apparent from the width of the coherent state in the  plot:
plot:
Another useful measure of the statistical properties of a state of
light is provided by a measure known as the second order temporal coherence function, commonly denoted  . The definition
of this function, for a classical state of light described by a
stationary intensity versus time distribution
. The definition
of this function, for a classical state of light described by a
stationary intensity versus time distribution  , is
, is

The numerator of this expression is a familiar autocorrelation
function; moreover, since  , it follows that
, it follows that  .
For a state of light described by some density matrix
.
For a state of light described by some density matrix  , we may
write a similar expression for
, we may
write a similar expression for  , but instead of
, but instead of
 , operators must be used, which act on
, operators must be used, which act on  . Letting
. Letting
 denote
denote  as usual, the quantum mechanical
definition of the second order temporal coherence function is
as usual, the quantum mechanical
definition of the second order temporal coherence function is

where we have used  and
and ![{\displaystyle [a,a^{\dagger }]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/671da8b1eb59fe1c04e601cc7963a6511d88c74e) . Note that this
expression, which is given for a single mode, has a value that is
independent of
. Note that this
expression, which is given for a single mode, has a value that is
independent of  . It is obtained by substituting quantum
operators for the electric field into the classical definition of
. It is obtained by substituting quantum
operators for the electric field into the classical definition of
 . In contrast to the classical case, the quantum
expression allows
. In contrast to the classical case, the quantum
expression allows  . In particular, the values of
. In particular, the values of
 , and the Fano factor (a measure of photon number
fluctuations relative to the Poisson distribution),
, and the Fano factor (a measure of photon number
fluctuations relative to the Poisson distribution),

are given for several important states of light in this table:
%
The Single Photon
So far, we have considered a variety of important multi-photon states,
in which typically  . What are the properties of a state of
a single photon?
First, keep in mind that
. What are the properties of a state of
a single photon?
First, keep in mind that  with
with  is not a
single photon state. That is a coherent state with an average of one
photon. In fact, the probabilities of finding
is not a
single photon state. That is a coherent state with an average of one
photon. In fact, the probabilities of finding  photons in this
state are:
photons in this
state are:
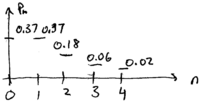
\noindent Thus, for example,  is mostly the vacuum
state
is mostly the vacuum
state  .
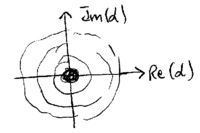
The true single photon state
.
The true single photon state  is an eigenstate of
is an eigenstate of  with
eigenvalue
with
eigenvalue  . This state can be generated, for example, by a
single atom emitting a photon into a cavity. The
. This state can be generated, for example, by a
single atom emitting a photon into a cavity. The  plot of
this state is a ring, since
plot of
this state is a ring, since

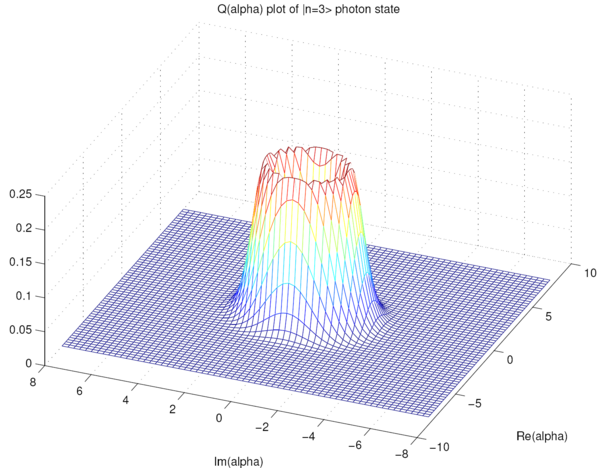
Here is a plot for a 3 photon state:
The single photon state is one of the most non-classical photon states
which can be created in the laboratory. Generating single photons at
a specific desired time, and with a desired frequency, is a challenge
at the forefront of much atomic physics today. One important
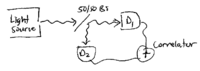
experimental signature of a single photon is obtained by performing a
Hanbury Brown-Twiss experiment, which measures the  intensity-intensity correlation function of photons from a single
source, split by a 50/50 beamsplitter:
intensity-intensity correlation function of photons from a single
source, split by a 50/50 beamsplitter:
Classically, photons incident on the beamsplitter are split equally
between the two paths. For equal distances between the beamsplitter
and the two detectors,  , and when the incident light is
coherent, the correlation is measured to be
, and when the incident light is
coherent, the correlation is measured to be  ; when it is chaotic,
as from a thermal source, it is measured to be
; when it is chaotic,
as from a thermal source, it is measured to be  , as given in the
table above. Classically, however,
, as given in the
table above. Classically, however,  can never be less
than
can never be less
than  .
.
However, when a single photon sourced into the beamsplitter, it exits
in a superposition of being in one or the other of the two paths, and
only one of the two detectors will ever click. This gives
 , as predicted by the quantum formula, but not
allowed by the classical expression.
, as predicted by the quantum formula, but not
allowed by the classical expression.
Here are some examples of experimental  measurements Single photon generation - experimental results.
measurements Single photon generation - experimental results.


![{\displaystyle H={\frac {1}{2}}\int \,d^{3}r\left[{\epsilon _{0}|{\vec {E}}|^{2}+{\frac {1}{\mu _{0}}}|{\vec {B}}|^{2}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6757b1d12769ae5a06329ce08be318f4d060019)






![{\displaystyle {\vec {E}}=i{\vec {e}}{\sqrt {\frac {\hbar \omega }{\epsilon _{0}V}}}\left[{ae^{i(kr-\omega t)}-a^{\dagger }e^{-i(kr-\omega t)}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b74b46b82cb4578fc67ec4b301250396178c7ec5)











![{\displaystyle {\begin{array}{rcl}a|n\rangle &=&{\sqrt {n}}|n-1{\rangle }\\a^{\dagger }|n\rangle &=&{\sqrt {n+1}}|n+1{\rangle }\\\,[a,a^{\dagger }]&=&1\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e69ce048473b86f8e3d8001a8805ee1a254f2c22)


































































![{\displaystyle [a,a^{\dagger }]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/671da8b1eb59fe1c04e601cc7963a6511d88c74e)