This section deals with how atoms behave in
static electric fields. The method is straightforward,
involving second order Rayleigh-Schrodinger perturbation
theory. The treatment describes the effects of symmetry on the
basic interaction, polarizability, and the concept of oscillator
strength.
Review of parity
Let us review the concept of parity. Parity is a consequence of space inversion.

We propose an operator that (in the spirit of the rotation operator introduced earlier) takes an initial ket and returns a ket with the above inversion operation performed.

We require that this operator in unitary and that it has the following key property (or, perhaps more precisely we define the operator through)

which implies

This shows that  is an eigenket of
is an eigenket of  with eigenvalue of
with eigenvalue of  . Finally, the eigenvalues of
. Finally, the eigenvalues of  are
are  and
and

Position is "odd" under space inversion or "odd under the parity operator". Angular momentum, on the other hand is even.

Because of this property position and momentum are called vectors or polar vectors and angular momentum is called an axial or psuedo vector.
What about wavefunction? What does the parity operator do to wavefunctions? Well it depends on the wavefunction. For example, consider the spherical harmonics (the angular part of the hydrogen atom eigenstates). Some of the wavefunctions are odd under parity and some are even. (In one dimension a cosine wave is "even" whereas a sine wave is "odd".)

Now, consider the case where a state is an energy eigenket and the parity operator commutes with Hamiltonian. Such a ket is not necessarily an eigenket of the parity operator. Consider, for example, the case of the hydrogen atom for  . Neglecting higher order pertubations to the hamiltonian,
. Neglecting higher order pertubations to the hamiltonian,  can be made up of a combination of two eigenkets with different parities,
can be made up of a combination of two eigenkets with different parities,

Without any degeneracies eigenstates of the hamiltonian are indeed eigenstates of the parity operator if the hamiltonian and  commute.
This idea of parity gives rise to what is called a selection rule. Selection rules, in general, are nothing more than the statement that certain operators connect certain states (
commute.
This idea of parity gives rise to what is called a selection rule. Selection rules, in general, are nothing more than the statement that certain operators connect certain states ( for certain
for certain  ) and do not connect other states (that is,
) and do not connect other states (that is,  for certain
for certain  ). Consider, for example, the
). Consider, for example, the  operator and two different parity eigenstates,
operator and two different parity eigenstates,

then

One can see this in the following way

which can be true only if  .
.  is an "parity odd operator" and it connects states of opposite parity. "Even operators" connect states of the same parity.
is an "parity odd operator" and it connects states of opposite parity. "Even operators" connect states of the same parity.
Atoms in a Static Electric Field
We can use this basic idea in understanding the problem of an atom subjected to an electric field. We begin by writing down the potential due to a collection of charges,

where

where  is the charge distribution.
is the charge distribution.  is the total charge,
is the total charge,  are the dipole moments,
are the dipole moments,  are the quadrupole moments, etc. The energy
are the quadrupole moments, etc. The energy  of an overall neutral collection of charges in an electric field
of an overall neutral collection of charges in an electric field  can similarly be expanded as
can similarly be expanded as

where  is the dipole and
is the dipole and  is the polarizability.
is the polarizability.
Now we are in a better position to solve the problem of the hydrogen atom in a static electric field,  , just about the simplest example.
, just about the simplest example.
The hamiltonian for this problem can be written

where  is the "unperturbed" hamiltonian for the hydrogen atom.
is the "unperturbed" hamiltonian for the hydrogen atom.
We chose to solve this via matrix methods. The first step is to write down the matrix elements for the hamiltonian is a basis of our choosing. Let's try with the  basis kets, the eigenkets of
basis kets, the eigenkets of  . So,
. So,  only contributes diagonal elements to the matrix,
only contributes diagonal elements to the matrix,  . As
. As  and
and  are scalars, not operators, we need only consider the effect of
are scalars, not operators, we need only consider the effect of  . First,
. First,  is a parity odd operator, connecting only states of different parity.
Thus
is a parity odd operator, connecting only states of different parity.
Thus  contributes nothing to the diagonal entries nor to any entries with the same angular momentum,
contributes nothing to the diagonal entries nor to any entries with the same angular momentum,  . States of the same parity but whose angular momentum differ by more than
. States of the same parity but whose angular momentum differ by more than  also result in zero because ... Finally,
also result in zero because ... Finally,  also only connects states of the same
also only connects states of the same  . One can see this by noting that
. One can see this by noting that

which is an even function in  . Any states differing by
. Any states differing by  would then result in an integral of two even functions (one of those being the
would then result in an integral of two even functions (one of those being the  originating from the
originating from the  ) and an odd function in
) and an odd function in  which is zero. This resulta can also be seen directly by noting a result of the Wigner-Eckhart theorem that
which is zero. This resulta can also be seen directly by noting a result of the Wigner-Eckhart theorem that  where
where  is just a number. Thus, we produce the "selection rules" for the
is just a number. Thus, we produce the "selection rules" for the  operator,
operator,

NOTE that this strictly applies only the this specific operator. If  were pointing in some other direction then things might (and do) change.
were pointing in some other direction then things might (and do) change.
The matrix for the our hamiltonian reads then

where the entries arranged in  order.
The 0's are designated with an indication of "why" those particular entries in the matrix are zero,
order.
The 0's are designated with an indication of "why" those particular entries in the matrix are zero,  meaning even/odd (
meaning even/odd ( selection rule) and
selection rule) and  meaning parity (
meaning parity ( selection rule. As mentioned above, the
selection rule. As mentioned above, the  contribution to the diagonal elements is zero due to parity. Because the
contribution to the diagonal elements is zero due to parity. Because the  states are degenerate, degenerate pertubation theory must be used to solve the problem. Of course we know that in reality the problem is more complex than this. Both fine, hyperfine and the Lamb shift have been neglected. Solving the problem taking this into account would indicate the use of second order pertubation theory.
states are degenerate, degenerate pertubation theory must be used to solve the problem. Of course we know that in reality the problem is more complex than this. Both fine, hyperfine and the Lamb shift have been neglected. Solving the problem taking this into account would indicate the use of second order pertubation theory.
To see how this all shakes out, let's go ahead and apply pertubation theory directly.

If one is in the case where this simple pertubation theory does not work because of degenerate states (leading to  in the denominator then it is best just to diagonalize the Hamiltonian in relation to
in the denominator then it is best just to diagonalize the Hamiltonian in relation to  . If you do that for the case of
. If you do that for the case of  you find that the eigenstates are
you find that the eigenstates are

where  is a constant. The last two states have a linear response to the electric field, or a linear Stark effect. Even is there were a small splitting between the different states in the
is a constant. The last two states have a linear response to the electric field, or a linear Stark effect. Even is there were a small splitting between the different states in the  manifold, if the field interaction were higher that the splitting then there would be also be a linear Stark effect. At lower fields the interaction would be second order (second order pertubation theory would be called for) and the response would be quadratic in the applied electric field. Notice the the new eigenstates are a mixture of states of different parity. This mixture allows for a dipole to be formed and it is the interaction of the electic field with this dipole that gives rise to a linear response to the field. It is this dipole that is talked about by chemists when they say that a molecule "has a dipole moment". Molecules "have dipole moments" because they have closely lying states of opposite parity so small fields put them in the linear Stark regime. But make no mistake, at low enough fields, the response would be quadratic, just as it is in the case of atoms.
manifold, if the field interaction were higher that the splitting then there would be also be a linear Stark effect. At lower fields the interaction would be second order (second order pertubation theory would be called for) and the response would be quadratic in the applied electric field. Notice the the new eigenstates are a mixture of states of different parity. This mixture allows for a dipole to be formed and it is the interaction of the electic field with this dipole that gives rise to a linear response to the field. It is this dipole that is talked about by chemists when they say that a molecule "has a dipole moment". Molecules "have dipole moments" because they have closely lying states of opposite parity so small fields put them in the linear Stark regime. But make no mistake, at low enough fields, the response would be quadratic, just as it is in the case of atoms.
Now, all of this has been talked about under the (essentially correct) assumption that
![{\displaystyle [H,\pi ]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d99e762688b1c8240c972dfa4261c1cc7d6b00) and, therefore, that the eigenstates of the H atom are also parity eigenstates. But what if
and, therefore, that the eigenstates of the H atom are also parity eigenstates. But what if
![{\displaystyle [H,\pi ]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdb19cc8d69e390bef7de1f0970c8d5bb991b618) ?
This occurs when the weak force is involved and will likely be present in nature and described, eventually, by extensions to the Standard Model. Such mechanisms can lead to the presence of permanent electic dipole moments of elementary particles.
?
This occurs when the weak force is involved and will likely be present in nature and described, eventually, by extensions to the Standard Model. Such mechanisms can lead to the presence of permanent electic dipole moments of elementary particles.
Some Results of Stationary Perturbation Theory
For reference, we recapitulate some elementary results from
perturbation theory. Assume that the Hamiltonian of a system may be
written as the sum of two parts

and that the eigenstates and eigenvalues of  are known:
are known:

If it is not possible to find the eigenvalues of  exactly,
it is possible to write power series expressions for them that
converge over some interval. If
exactly,
it is possible to write power series expressions for them that
converge over some interval. If  is time independent,
the problem is stationary and the appropriate perturbation theory
is Rayleigh- Schrodinger stationary state perturbation
theory, described in most texts in quantum
mechanics. We write
is time independent,
the problem is stationary and the appropriate perturbation theory
is Rayleigh- Schrodinger stationary state perturbation
theory, described in most texts in quantum
mechanics. We write


and express the  order perturbation in terms of
order perturbation in terms of
 and
and  . The energies are
given by
. The energies are
given by

We shall only use the lowest two orders here. The first order
results are


The symbol  indicates that the term
indicates that the term  is
excluded. It
is understood that the sum extends over continuum states. Note that
the state function is nor properly normalized, but that the error
is
quadratic in
is
excluded. It
is understood that the sum extends over continuum states. Note that
the state function is nor properly normalized, but that the error
is
quadratic in  .
.
The second order results are
![{\displaystyle {\begin{array}{rcl}E_{n}^{(2)}&=&\sum '_{n}{\frac {|\langle m|H^{\prime }|n\rangle |^{2}}{E_{n}-E_{m}}}\\|n^{(2)}{\rangle }&=&\sum '_{m}|m\rangle {\left[{\frac {\langle m|H^{\prime }|n{\rangle }}{E_{n}-E_{m}}}{\left[1-{\frac {\langle n|H^{\prime }|n{\rangle }}{E_{n}-E_{m}}}\right]}+\sum '_{p}{\frac {\langle m|H^{\prime }|p\rangle \langle p|H^{\prime }|n{\rangle }}{(E_{n}-E_{m})(E_{n}-E_{p})}}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/732691c83d301fabf34c07b000262d519f0855f9)
In second order perturbation theory the effect of a coupling of  and
and  by
by  is to push the levels apart, independent of the
value of
is to push the levels apart, independent of the
value of  . Consequently, states coupled by
. Consequently, states coupled by  always repel each other.
always repel each other.
Perturbation Theory of Polarizability
We turn now to finding the energy and polarizability of an atom in
a static field along the +z direction. We apply perturbation
theory taking  to describe the unperturbed atomic system and
to describe the unperturbed atomic system and

As discussed in Sect.\ \ref{SEC_rp}, parity requires that
 so
the first order perturbation vanishes. To second order, the energy
is given by
so
the first order perturbation vanishes. To second order, the energy
is given by

If we compare this results with the potential energy of a charge
distribution interacting with an electric field, (Eq.\
\ref{EQ_aefone}), we can identify the polarizability interaction
with the second term in this equation. As a result the
polarizability in state  is given by
is given by

Note that this has the dimensions of length , i.e. volume.
, i.e. volume.
The induced dipole moment can be found from the polarization.

An alternative way to calculate the dipole moment is to calculate
the
expectation value of the dipole operator, Eq.\ \ref{EQ_aefthree},
using the first order perturbed state vector.

![{\displaystyle =2{\rm {Re}}[\langle n^{(0)}|d|n^{(1)}\rangle ]=2e^{2}{\rm {Re}}{\left[\sum _{s,m}{\frac {\langle n^{(0)}|s|m\rangle \langle m|z|n^{(0)}\rangle }{E_{m}-E_{n}}}\right]}{\hat {s}}\cdot {\hat {z}}{\mathcal {E}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afd33952a21990436ab03840a4b4e1e286b70684)
where the sum is over  Only the term
Only the term  will
contribute, and it will yield an interaction energy in agreement
with
Eq.\ \ref{EQ_polartwo}.
will
contribute, and it will yield an interaction energy in agreement
with
Eq.\ \ref{EQ_polartwo}.
As an example, for the ground state of hydrogen we can obtain a
lower limit for the polarizability by considering only the
contribution to the sum of the  state. Values for the various
moments in hydrogen are given in Bethe and Salpeter, Section 63.
Using
state. Values for the various
moments in hydrogen are given in Bethe and Salpeter, Section 63.
Using  = 1.666, and
= 1.666, and  , we obtain
, we obtain  atomic units (i.e.
atomic units (i.e.  ).
).
The polarizability of the ground state of hydrogen can be
calculated exactly. It turns out that the  state makes the
major contribution, and that the higher bound states contribute
relatively little. However, the continuum makes a significant
contributions. The exact value is 4.5.
state makes the
major contribution, and that the higher bound states contribute
relatively little. However, the continuum makes a significant
contributions. The exact value is 4.5.
To put this polarizability in perspective, note that the potential
of a conducting sphere of radius  in a uniform electric field
in a uniform electric field
 is given by
is given by

The induced dipole moment is  , so that the
polarizability is
, so that the
polarizability is  . For the ground state of hydrogen,
. For the ground state of hydrogen,
 , so to a crude approximation, in an electric
field hydrogen behaves like a conducting sphere.
, so to a crude approximation, in an electric
field hydrogen behaves like a conducting sphere.
Polarizability may be approximated easily, though not accurately,
using Unsold's approximation in which the energy term in the
denominator of Eq.\ \ref{EQ_polarsix} is replaced by an average
energy interval  . The sum can then be
evaluated using the closure rule
. The sum can then be
evaluated using the closure rule  . (Note
that the term
. (Note
that the term  does not need to be excluded from the sum,
since
does not need to be excluded from the sum,
since  .). With this approximation,
.). With this approximation,

For hydrogen in the ground state,  . If we
take the average excitation energy to be
. If we
take the average excitation energy to be  ,
the result is
,
the result is  .
.
Atoms in an Oscillating Electric Field
There is a close connection between the behavior of an atom in a
static electric field and its response to an oscillating field,
i.e. a connection between the Stark effect and radiation
processes. In the former case, the field induces a static dipole
moment; in the latter case, it induces an oscillating moment. An
oscillating moment creates an oscillating macroscopic
polarization and leads to the absorption and emission of
radiation. We shall calculate the response of an atom to an
oscillating field

where  is the polarization vector for the field. For
a weak field the time varying state
of this system can be found from first order time dependent
perturbation theory. We shall write
the electric dipole operator as D = -er. (This is a
change of notation. Previously the
symbol was d.) The Hamiltonian naturally separates into two
parts,
is the polarization vector for the field. For
a weak field the time varying state
of this system can be found from first order time dependent
perturbation theory. We shall write
the electric dipole operator as D = -er. (This is a
change of notation. Previously the
symbol was d.) The Hamiltonian naturally separates into two
parts,  ,
where
,
where  is the unperturbed Hamiltonian and
is the unperturbed Hamiltonian and

We shall express the solution of the time dependent Schroedinger
equation in terms of the
eigenstates of  .
.

where  . Because of the perturbation
. Because of the perturbation
 , the
, the  's become time
dependent, and we have
's become time
dependent, and we have

Left multiplying the final two expressions by  to
project out the
to
project out the  -th terms yields
-th terms yields

where  . In perturbation theory,
this set of equations is solved
by a set of approximations to
. In perturbation theory,
this set of equations is solved
by a set of approximations to  labeled
labeled  .
Starting with
.
Starting with

one sets

and solves for the successive approximations by integration.
We now apply this to the problem of an atom which is in its ground
state  at
at  , and which is
subject to the interaction of Eq.\ \ref{EQ_atomoef2}. Consequently
, and which is
subject to the interaction of Eq.\ \ref{EQ_atomoef2}. Consequently
 ,
,  . Substituting in Eq.\ \ref{EQ_atomoef7} and integrating
from
. Substituting in Eq.\ \ref{EQ_atomoef7} and integrating
from  to
to  gives
gives
![{\displaystyle {\begin{array}{rcl}a_{k}^{(1)}(t)&=&(i\hbar )^{-1}\int _{0}^{t}dt^{\prime }\langle k|H^{\prime }(t^{\prime })|g\rangle e^{i\omega _{kg}t^{\prime }}\\&=&-(i\hbar )^{-1}\langle k|{\hat {e}}\cdot D|g\rangle {\frac {\mathcal {E}}{2}}\int _{0}^{t}dt^{\prime }{\left[e^{i(\omega _{kg}+\omega )t^{\prime }}+e^{i(\omega _{kg}-\omega )t^{\prime }}\right]}\\&=&{\frac {\mathcal {E}}{2\hbar }}\langle k|{\hat {e}}\cdot D|g\rangle {\left[{\frac {e^{i(\omega _{kg}+\omega )t}-1}{\omega _{kg}+\omega }}+{\frac {e^{i(\omega _{kg}-\omega )t}-1}{\omega _{kg}-\omega }}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d5e4872c67deeb9e95cc30b7f74ecd1122ce0f)
The -1 terms in the square bracketed term arises because it is
assumed that the field was turned on
instantaneously at  . They represent transients that rapidly
damp and can be neglected.
. They represent transients that rapidly
damp and can be neglected.
The term with  , in the denominator is the
counter-rotating term. It can be
neglected if one is considering cases where
, in the denominator is the
counter-rotating term. It can be
neglected if one is considering cases where  (i.e. near resonance), but
we shall retain both terms and calculate the expectation value of
the first order time dependent
dipole operator
(i.e. near resonance), but
we shall retain both terms and calculate the expectation value of
the first order time dependent
dipole operator 
![{\displaystyle {\begin{array}{rcl}\langle D(\omega ,t)\rangle &=&2{\rm {Re}}{\left\{\langle g|{\bf {D}}|\sum _{k}a_{k}^{(1)}(t)e^{-i\omega _{kg}}|k\rangle \right\}}\\&=&{\mathcal {E}}{\rm {Re}}{\left[\sum _{k}{\frac {\langle g|D|k\rangle \langle k|{\hat {e}}\cdot D|g\rangle }{\hbar }}{\left\{{\frac {e^{i\omega t}}{\omega _{kg}+\omega }}+{\frac {e^{-i\omega t}}{\omega _{kg}-\omega }}\right\}}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bd4119db9415e85baec8331b26488d24624bfc)
If we consider the case of linearly polarized light  , then
, then

We can write  in terms of a polarizability
in terms of a polarizability  :
:

This result diverges if  . Later,
when we introduce radiative damping, the divergence will be
avoided in the usual way.
. Later,
when we introduce radiative damping, the divergence will be
avoided in the usual way.
Oscillator Strength
Eq.\ \ref{EQ_atomoef11} resemble the oscillating dipole moment of a
system of classical
oscillators. Consider a set of oscillators having charge  ,
mass
,
mass  , and natural frequency
, and natural frequency
 , driven by the field
, driven by the field  . The
amplitude of the motion is given
by
. The
amplitude of the motion is given
by

If we have a set of such oscillators, then the total oscillating
moment is given by

This is strongly reminiscent of Eq.\ \ref{EQ_atomoef10}. It is
useful to introduce the concept of
oscillator strength, a dimensionless quantity defined as

where  and
and  are any two eigenstates. Note that
are any two eigenstates. Note that
 is positive if
is positive if  , i.e. for absoprtion, and negative if
, i.e. for absoprtion, and negative if
 Then, Eq.\ \ref{EQ_atomoef10} becomes
Then, Eq.\ \ref{EQ_atomoef10} becomes

Comparing this with Eq.\ \ref{EQ_ostre2}, we see that the behavior
of an atom in an oscillating
field mimics a set of classical oscillators with the same
frequencies as the eigenfrequencies of
the atom, but having effective charge strengths  .\\
.\\
The oscillator strength is useful for characterizing radiative
interactions and also the
susceptibiltiy of atoms. It satisfies an important sum rule, the
Thomas-Reiche-Kuhn sum rule:

We prove by considering the general Hamiltonian

Using the commutator relation
![{\displaystyle [A,B^{2}]=[A,B]B+B[A,B],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e16bcf41c2c00f41091a8b2f6ec1a54c3c26aa3)
and the relation ![{\displaystyle [r_{j},p_{k}]=i\hbar \delta _{jk}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47639ff8ac69b050c5dc9d8cf58f9c6d17af6a3) , we have
, we have
![{\displaystyle [r,H]={\frac {i\hbar }{m}}p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/335156c1e95f556b5ff6979d61bd8c1ef0ea7263)
where  , and
, and  .
However,
.
However,
![{\displaystyle \langle j|[r,H]|k\rangle =(E_{k}-E_{n})\langle j|r|k\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4756f9f0266fc68ae7c3ce2a7995ae930e09add7)
Consequently,

where  . Thus, we can write
Eq.\ \ref{EQ_ostre3} in either of two forms:
. Thus, we can write
Eq.\ \ref{EQ_ostre3} in either of two forms:

Taking half the sum of these equations and using the closure
relation  , we have
, we have
![{\displaystyle \sum _{k}f_{kj}={\frac {i}{\hbar }}{\left[\langle j|p_{z}z-zp_{z}|j\rangle \right]}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9256c4cbcfdc8f1d87d37c52474b7279a2ec1990)
We have calculated this for a one-electron atom, but the
application to a Z-electron atom is
straightforward because the Hamiltonian in Eq.\ \ref{EQ_ostre6}
is quite general. In this case

Here  is some eigenstate of the system, and the index
is some eigenstate of the system, and the index  describes all the eigenstates of all
the electrons -- including continuum states. In cases where only
a single electron will be
excited, however, for instance in the optical regime of a
"single-electron" atom where the inner core
electrons are essentially unaffected by the radiation, the atom
behaves as if it were a single electron system with
describes all the eigenstates of all
the electrons -- including continuum states. In cases where only
a single electron will be
excited, however, for instance in the optical regime of a
"single-electron" atom where the inner core
electrons are essentially unaffected by the radiation, the atom
behaves as if it were a single electron system with  .
.
Note that  is positive if
is positive if  , i.e. if the final
state lies above the initial state. Such a transition corresponds to
absorption of a photon. Since
, i.e. if the final
state lies above the initial state. Such a transition corresponds to
absorption of a photon. Since  , the oscillator strength
for emission of a photon is negative.
, the oscillator strength
for emission of a photon is negative.
Our definition of oscillator strength, Eq.\ \ref{EQ_ostre3},
singles out a particular axis, the  -axis, fixed by the
polarization of the light. Consequently, it depends on the orientation
of the atom in the initial state and final states. It is convenient to
introduce the average oscillator
strength (often simply called the oscillator strength), by
letting
-axis, fixed by the
polarization of the light. Consequently, it depends on the orientation
of the atom in the initial state and final states. It is convenient to
introduce the average oscillator
strength (often simply called the oscillator strength), by
letting  , summing over the initial
, summing over the initial  state and averaging over the
final state.\\
state and averaging over the
final state.\\

(This is the conversion followed by Sobelman.) It is evident that

where  is the multiplicity factor for state
is the multiplicity factor for state  . An
extensive discussion of the sum rules and
their applications to oscillator strengths and transition
momentums can be found in Bethe and
Salpeter, section 6.1. Among the interesting features they point
out is that transitions from an
initial state
. An
extensive discussion of the sum rules and
their applications to oscillator strengths and transition
momentums can be found in Bethe and
Salpeter, section 6.1. Among the interesting features they point
out is that transitions from an
initial state  to a final state
to a final state  on the average have
stronger oscillator strengths for absorption if
on the average have
stronger oscillator strengths for absorption if  , and stronger oscillator
strengths for emission if
, and stronger oscillator
strengths for emission if  . In other words,
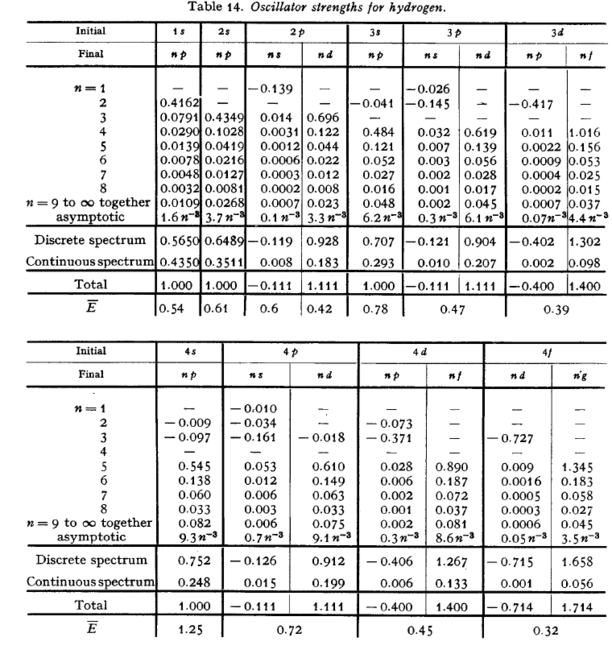
atoms "like" to increase their
angular momentum on absorption of a photon, and decrease it on
emission. The following page gives
a table of oscillator strengths for hydrogen in which this
tendency can be readily identified.
(Taken from {\it The Quantum Mechanics of One- and Two-Electron Atoms}, H.A. Bethe and E.E. Salpeter, Academic Press (1957).)
. In other words,
atoms "like" to increase their
angular momentum on absorption of a photon, and decrease it on
emission. The following page gives
a table of oscillator strengths for hydrogen in which this
tendency can be readily identified.
(Taken from {\it The Quantum Mechanics of One- and Two-Electron Atoms}, H.A. Bethe and E.E. Salpeter, Academic Press (1957).)
\caption{
Oscillator strengths for hydrogen. From
Mechanics of One- and Two-Electron Atoms}
References






























































![{\displaystyle [H,\pi ]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d99e762688b1c8240c972dfa4261c1cc7d6b00)
![{\displaystyle [H,\pi ]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdb19cc8d69e390bef7de1f0970c8d5bb991b618)













![{\displaystyle {\begin{array}{rcl}E_{n}^{(2)}&=&\sum '_{n}{\frac {|\langle m|H^{\prime }|n\rangle |^{2}}{E_{n}-E_{m}}}\\|n^{(2)}{\rangle }&=&\sum '_{m}|m\rangle {\left[{\frac {\langle m|H^{\prime }|n{\rangle }}{E_{n}-E_{m}}}{\left[1-{\frac {\langle n|H^{\prime }|n{\rangle }}{E_{n}-E_{m}}}\right]}+\sum '_{p}{\frac {\langle m|H^{\prime }|p\rangle \langle p|H^{\prime }|n{\rangle }}{(E_{n}-E_{m})(E_{n}-E_{p})}}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/732691c83d301fabf34c07b000262d519f0855f9)









![{\displaystyle =2{\rm {Re}}[\langle n^{(0)}|d|n^{(1)}\rangle ]=2e^{2}{\rm {Re}}{\left[\sum _{s,m}{\frac {\langle n^{(0)}|s|m\rangle \langle m|z|n^{(0)}\rangle }{E_{m}-E_{n}}}\right]}{\hat {s}}\cdot {\hat {z}}{\mathcal {E}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afd33952a21990436ab03840a4b4e1e286b70684)












































![{\displaystyle {\begin{array}{rcl}a_{k}^{(1)}(t)&=&(i\hbar )^{-1}\int _{0}^{t}dt^{\prime }\langle k|H^{\prime }(t^{\prime })|g\rangle e^{i\omega _{kg}t^{\prime }}\\&=&-(i\hbar )^{-1}\langle k|{\hat {e}}\cdot D|g\rangle {\frac {\mathcal {E}}{2}}\int _{0}^{t}dt^{\prime }{\left[e^{i(\omega _{kg}+\omega )t^{\prime }}+e^{i(\omega _{kg}-\omega )t^{\prime }}\right]}\\&=&{\frac {\mathcal {E}}{2\hbar }}\langle k|{\hat {e}}\cdot D|g\rangle {\left[{\frac {e^{i(\omega _{kg}+\omega )t}-1}{\omega _{kg}+\omega }}+{\frac {e^{i(\omega _{kg}-\omega )t}-1}{\omega _{kg}-\omega }}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d5e4872c67deeb9e95cc30b7f74ecd1122ce0f)



![{\displaystyle {\begin{array}{rcl}\langle D(\omega ,t)\rangle &=&2{\rm {Re}}{\left\{\langle g|{\bf {D}}|\sum _{k}a_{k}^{(1)}(t)e^{-i\omega _{kg}}|k\rangle \right\}}\\&=&{\mathcal {E}}{\rm {Re}}{\left[\sum _{k}{\frac {\langle g|D|k\rangle \langle k|{\hat {e}}\cdot D|g\rangle }{\hbar }}{\left\{{\frac {e^{i\omega t}}{\omega _{kg}+\omega }}+{\frac {e^{-i\omega t}}{\omega _{kg}-\omega }}\right\}}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bd4119db9415e85baec8331b26488d24624bfc)




















![{\displaystyle [A,B^{2}]=[A,B]B+B[A,B],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e16bcf41c2c00f41091a8b2f6ec1a54c3c26aa3)
![{\displaystyle [r_{j},p_{k}]=i\hbar \delta _{jk}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47639ff8ac69b050c5dc9d8cf58f9c6d17af6a3)
![{\displaystyle [r,H]={\frac {i\hbar }{m}}p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/335156c1e95f556b5ff6979d61bd8c1ef0ea7263)


![{\displaystyle \langle j|[r,H]|k\rangle =(E_{k}-E_{n})\langle j|r|k\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4756f9f0266fc68ae7c3ce2a7995ae930e09add7)




![{\displaystyle \sum _{k}f_{kj}={\frac {i}{\hbar }}{\left[\langle j|p_{z}z-zp_{z}|j\rangle \right]}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9256c4cbcfdc8f1d87d37c52474b7279a2ec1990)