Atoms in electric fields
This section deals with how atoms behave in static electric fields. The method is straightforward, involving second order perturbation theory. The treatment describes the effects of symmetry on the basic interaction, polarizability, and the concept of oscillator strength.
Contents
- 1 Review: Parity
- 2 Review: Results of Stationary Perturbation Theory
- 3 Supplement: The Hydrogen Atom in a Static Electric Field
- 4 Perturbation Theory of Polarizability
- 5 Beyond the quadratic Stark effect
- 6 Field ionization
- 7 Atoms in an Oscillating Electric Field
- 8 Oscillator Strength
- 9 Index of refraction
- 10 References
Review: Parity
Review: Results of Stationary Perturbation Theory
Supplement: The Hydrogen Atom in a Static Electric Field
Perturbation Theory of Polarizability
We will find the energy and polarizability of an atom in a static field along the +z direction. We apply perturbation theory taking to describe the unperturbed atomic system and
Non-degenerate eigenstates have to be eigenstates of parity. Since is odd under parity operation, parity requires that . So the first order perturbation vanishes. To second order, the energy is given by
If we define now the polarizability in state as
- {EQ_polarsix}
we obtain
The dipole moment is the expectation value of the dipole operator, using the first order perturbed state vector.
where the sum is over Only the term will contribute, and we can express the induced dipole moment by the polarizability:
Note that the Stark shift is and not equal to . is the expectation value for the electrostatic potential energy of the dipole moment, but the total energy change is only one half of this since energy is needed to admix excited states into the ground state.
Note that polarizability has the dimensions of length, i.e. volume. As an example, for the ground state of hydrogen we can obtain a lower limit for the polarizability by considering only the contribution to the sum of the state. Values for the various moments in hydrogen are given in Bethe and Salpeter, Section 63. Using = 1.666, and , we obtain atomic units (i.e. ).
The polarizability of the ground state of hydrogen can be calculated exactly. It turns out that the state makes the major contribution, and that the higher bound states contribute relatively little. However, the continuum makes a significant contributions. The exact value is 4.5.
To put the above result for the polarizability in perspective, note that the potential of a conducting sphere of radius in a uniform electric field is given by
The induced dipole moment is , so that the polarizability is . For the ground state of hydrogen, , so to a crude approximation, in an electric field hydrogen behaves like a conducting sphere.
Polarizability may be approximated easily, though not accurately, using Unsold's approximation in which the energy term in the denominator of Eq. \ref{EQ_polarsix} is replaced by an average energy interval . The sum can then be evaluated using the closure rule . (Note that the term does not need to be excluded from the sum, since .). With this approximation,
For hydrogen in the ground state, . If we take the average excitation energy to be , the result is .
If we use the virial theorem for the ground state energy, and use we obtain
which shows that the polarizability is related to the atomic volume.
Beyond the quadratic Stark effect
It should be obvious from the previous discussion that the Stark effect for a state of is quadratic only when
(EQ_ beyondone)
when is the nearest state of opposite parity to .
If is the ground state, we can expect Hartree and (virial theorem). Hence the Stark shift should be quadratic if the field is well below the critical value
(EQ_ beyondtwo)
[ is atomic unit of field] —a field three orders of magnitude in excess of what can be produced in a laboratory except in a vanishingly small volume.
If is an excited state, say , this situation changes dramatically. In general, the matrix element and to the next level of opposite parity depends on the quantum defect:
(EQ_ beyondthree)
Thus the critical field is lowered to
(EQ_ beyondfour)
Considering that quantum defects are typically when is the largest of an electron in the core), it is clear that even 1 V/cm fields will exceed for higher levels if . Large laboratory fields ( V/cm) can exceed even for states if .
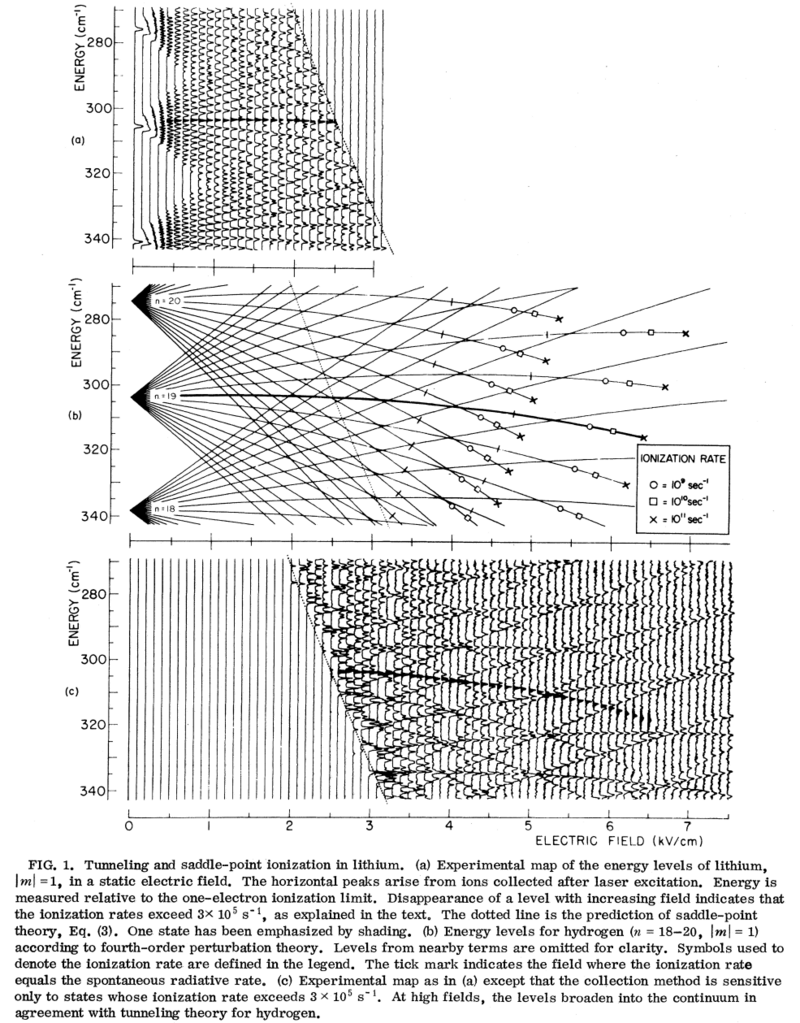
When the electric field exceeds states with different but the same are degenerate to the extent that their quantum defects are small. Once exceeds the number of core electrons, these states will easily become completely mixed by the field and they must be diagonalized exactly. The result is eigenstates possessing apparently permanent electric dipoles with a resulting linear Stark shift (see following figure). As the field increases, these states spread out in energy. First they run into states with the same but different quantum defects; then the groups of states with different begin to overlap. At this point a matrix containing all states with greater or equal to must be diagonalized. Only the lowest states do not partake in this strong mixing.
The situation described above differs qualitatively for hydrogen since it has no quantum defects and the energies are degenerate. In this case the zero-field problem may be solved using a basis which diagonalizes the Hamiltonian both for the atom above and also in the presence of an electric field. This approach corresponds to solving the H atom in parabolic–ellipsoidal coordinates and results in the presence of an integral quantum number which replaces . The resulting states possess permanent dipole moments which vary with this quantum number and therefore have linear Stark effects even in infinitesimal fields. Moreover the matrix elements which mix states from different manifolds vanish at all fields, so the upper energy levels from one manifold cross the lower energy levels from the manifold above without interacting with them.
The following example shows the high field Stark effect for Li. Only the term in Li has an appreciable quantum defect, and it has been suppressed by selecting final states with .
The dramatic difference between the physical properties of atoms with and the properties of the same atoms in their ground state, coupled with the fact that these properties are largely independent of the type of atom which is excited, justifies the application of the name Rydberg atoms to highly excited atoms in general. Rydberg atoms have been pioneered by the groups of Kleppner, Haroche, Walther.
\caption{ Stark effect and field ionization in Li for levels with . Each vertical line in (a)represents a measurement at that field of the number of atoms excited (from the state) by radiation whose energy falls the indicated amount below the ionization limit. Thus the patterns made by absorption peaks at successive field strengths represent the behavior of the energy levels with increasing field. At zero field the levels group according to the principal quantum number ; at intermediate field the levels display a roughly linear Stark effect, and at high fields they disappear owing to field ionization. The solid line is the classically predicted ionization field (see next section). Figure taken from M.G. Littman, M.M. Kash and D. Kleppner, Phys. Rev. Lett. 41, 103–107 (1978).}
Field ionization
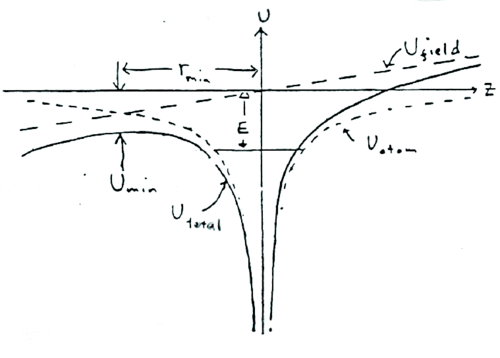
If an atom is placed in a sufficiently high electric field it will be ionized, a process called field ionization . An excellent order of magnitude estimate of the field , required to ionize an atom which is initially in a level bound by energy can be obtained by the following purely classical argument: the presence of the field adds the term to the potential energy of the atom. This produces a potential with a maximum and the atom will ionize if .
The figure shows the combined potential as well as and .
\caption{Potential diagram for field ionization. }
(EQ_ fieldionone)
The appropriate maximum occurs at
(EQ_ fieldiontwo)
as determined from . Equating and gives
(EQ_ fieldionthree)
for level with energy and quantum number .
The predictions of this formula for is usually accurate within 20% in spite of its neglect of both quantum tunneling and the change in produced by the field. Tunneling manifests itself as a finite decay rate for states which classically lie lower than the barrier. The increase of the ionization rate with field is so dramatic, however, that the details of the experiment do not influence the field at which ionization occurs very much: calculations [u'BHR65'] show the ionization rate increasing from /sec to /sec for a 30% increase in the field.
Oddly enough the classical prediction works worse for H than for any other atom. This is a reflection of the fact that certain matrix elements necessary to mix the states (so the wave function samples the region near ) are rigorously zero in H, as discussed in the preceding part of this section. Hence the orbital ellipse of the electron does not precess and can remain on the side of the nucleus. There its energy will increase with , but it will not spill over the lip of the potential and ionize.
Field ionization is an important technique with applications in applied and fundamental science. Its important feature is close to 100 % detection efficiency for atoms excited to Rydberg states.
Applied application: Detection of trace elements. After Chernobyl, field ionization techniques were refined to detect radioactive strontium isotopes or other radio-isotopes. The spectroscopic scheme was excitation to Rydberg states (which is isotope specific thanks to isotope shifts), followed by field ionization. See, e.g. Wendt et al., Physica Scripta T58, 104-108 (1995).
Fundamental physics: Field ionization has been used by Haroche's and Walther's group for a series of studies of Rydberg atoms exchanging photons with a microwave cavity, e.g. for the single atom maser experiment, or for other QED studies. See, e.g. Brune et al., Phys. Rev. Lett. 76, 1800 (1996).
Atoms in an Oscillating Electric Field
There is a close connection between the behavior of an atom in a static electric field and its response to an oscillating field, i.e. a connection between the Stark effect and radiation processes. In the former case, the field induces a static dipole moment; in the latter case, it induces an oscillating moment. An oscillating moment creates an oscillating macroscopic polarization and leads to the absorption and emission of radiation. We shall calculate the response of an atom to an oscillating field
where is the polarization vector for the field. For a weak field the time varying state of this system can be found from first order time dependent perturbation theory. We shall write the electric dipole operator as D = -er. (This is a change of notation. Previously the symbol was d.) The Hamiltonian naturally separates into two parts, , where is the unperturbed Hamiltonian and
{EQ_atomoef2}
We shall express the solution of the time dependent Schroedinger equation in terms of the eigenstates of .
where . Because of the perturbation , the 's become time dependent, and we have
Left multiplying the final two expressions by to project out the -th terms yields
where . In perturbation theory, this set of equations is solved by a set of approximations to labeled . Starting with
one sets
{EQ_atomoef7}
and solves for the successive approximations by integration.
We now apply this to the problem of an atom which is in its ground state at , and which is subject to the interaction of Eq. \ref{EQ_atomoef2}. Consequently , . Substituting in Eq. \ref{EQ_atomoef7} and integrating from to gives
The -1 terms in the square bracketed term arises because it is assumed that the field was turned on instantaneously at . They represent transients that rapidly damp and can be neglected.
The term with , in the denominator is the counter-rotating term. It can be neglected if one is considering cases where (i.e. near resonance), but we shall retain both terms and calculate the expectation value of the first order time dependent dipole operator
If we consider the case of linearly polarized light , then
{EQ_atomoef10}
We can write in terms of a polarizability :
{EQ_atomoef11}
This result diverges if . Later, when we introduce radiative damping, the divergence will be avoided in the usual way. The AC Stark shift is given by where the bar denotes the time average over the rapidly oscillating electric field.
For one retrieves the result for the DC Stark effect. Note that in the DC limit, the co- and counter-rotation terms contribute equally.
To be added: Discussion of the result in the dressed atom picture
Oscillator Strength
Eq.\ \ref{EQ_atomoef11} resemble the oscillating dipole moment of a system of classical oscillators. Consider a set of oscillators having charge , mass , and natural frequency , driven by the field . The amplitude of the motion is given by
If we have a set of such oscillators, then the total oscillating moment is given by
{EQ_ostre2}
This is strongly reminiscent of Eq. \ref{EQ_atomoef10}. It is useful to introduce the concept of oscillator strength, a dimensionless quantity defined as
where and are any two eigenstates. Note that is positive if , i.e. for absoprtion, and negative if Then, Eq. \ref{EQ_atomoef10} becomes
Comparing this with Eq. \ref{EQ_ostre2}, we see that the behavior of an atom in an oscillating field mimics a set of classical oscillators with the same frequencies as the eigenfrequencies of the atom, but having effective charge strengths .\\
The oscillator strength is useful for characterizing radiative interactions and also the susceptibiltiy of atoms. It satisfies an important sum rule, the Thomas-Reiche-Kuhn sum rule:
We prove by considering the general Hamiltonian
Using the commutator relation
and the relation , we have
where , and . However,
Consequently,
where . Thus, we can write Eq.\ \ref{EQ_ostre3} in either of two forms:
Taking half the sum of these equations and using the closure relation , we have
We have calculated this for a one-electron atom, but the application to a Z-electron atom is straightforward because the Hamiltonian in Eq.\ \ref{EQ_ostre6} is quite general. In this case
Here is some eigenstate of the system, and the index describes all the eigenstates of all the electrons -- including continuum states. In cases where only a single electron will be excited, however, for instance in the optical regime of a "single-electron" atom where the inner core electrons are essentially unaffected by the radiation, the atom behaves as if it were a single electron system with .
Note that is positive if , i.e. if the final state lies above the initial state. Such a transition corresponds to absorption of a photon. Since , the oscillator strength for emission of a photon is negative.
Our definition of oscillator strength, Eq.\ \ref{EQ_ostre3}, singles out a particular axis, the -axis, fixed by the polarization of the light. Consequently, it depends on the orientation of the atom in the initial state and final states. It is convenient to introduce the average oscillator strength (often simply called the oscillator strength), by letting , summing over the initial state and averaging over the final state.\\
(This is the conversion followed by Sobelman.) It is evident that
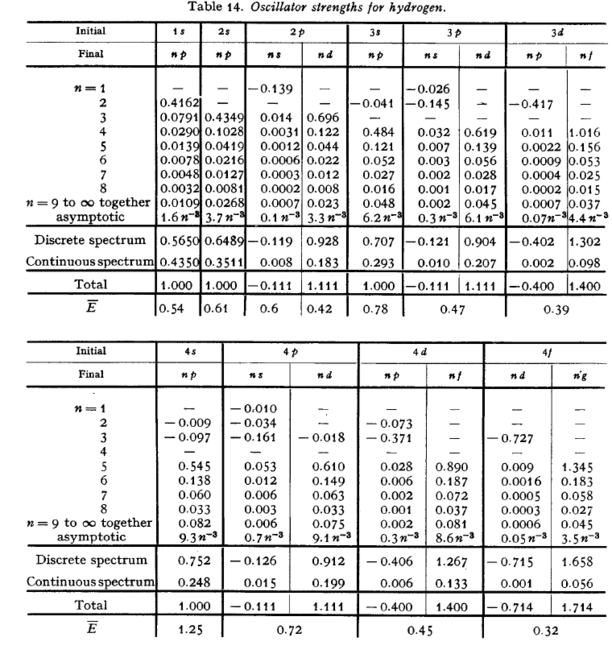
where is the multiplicity factor for state . An extensive discussion of the sum rules and their applications to oscillator strengths and transition momentums can be found in Bethe and Salpeter, section 6.1. Among the interesting features they point out is that transitions from an initial state to a final state on the average have stronger oscillator strengths for absorption if , and stronger oscillator strengths for emission if . In other words, atoms "like" to increase their angular momentum on absorption of a photon, and decrease it on emission. The following page gives a table of oscillator strengths for hydrogen in which this tendency can be readily identified. (Taken from {\it The Quantum Mechanics of One- and Two-Electron Atoms}, H.A. Bethe and E.E. Salpeter, Academic Press (1957).)
\caption{ Oscillator strengths for hydrogen. From Mechanics of One- and Two-Electron Atoms}
Index of refraction
As an application of the expression for the ac polarizability, we now discuss the index of refraction of an atomic gas. What we derive here, is fully sufficient to understand both absorption imaging and phase-contrast imaging used to observe ultracold atomic clouds.
In the case of near resonant light we can neglect the counter-rotating term, and let
Define the natural linewidth (this expression is derived later in the course)
So we can rewrite the expression for the refractive index:
where, since
we have
In our derivation of the polarizability, we didn't include any damping. The effect of damping is to give the refractive index an imaginary (absorptive) part. Damping can be included by adding an imaginary part to the detuning :
where the first term in brackets corresponds to dispersion and the second to absorption. This become obvious when one propagates the wave with the wavevector modified by the index of refraction:
The optical density on resonance is:
Note: When the linewidth is determined by spontaneous emission then , and the dispersive phase shift is
The maximum phase shift occurs at a detuning of









![{\displaystyle =2{\rm {Re}}[\langle n^{(0)}|d|n^{(1)}\rangle ]=2e^{2}{\rm {Re}}{\left[\sum _{s,m}{\frac {\langle n^{(0)}|s|m\rangle \langle m|z|n^{(0)}\rangle }{E_{m}-E_{n}}}\right]}{\hat {s}}\cdot {\hat {z}}{\mathcal {E}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afd33952a21990436ab03840a4b4e1e286b70684)




































































































![{\displaystyle {\begin{array}{rcl}a_{k}^{(1)}(t)&=&(i\hbar )^{-1}\int _{0}^{t}dt^{\prime }\langle k|H^{\prime }(t^{\prime })|g\rangle e^{i\omega _{kg}t^{\prime }}\\&=&-(i\hbar )^{-1}\langle k|{\hat {e}}\cdot D|g\rangle {\frac {\mathcal {E}}{2}}\int _{0}^{t}dt^{\prime }{\left[e^{i(\omega _{kg}+\omega )t^{\prime }}+e^{i(\omega _{kg}-\omega )t^{\prime }}\right]}\\&=&{\frac {\mathcal {E}}{2\hbar }}\langle k|{\hat {e}}\cdot D|g\rangle {\left[{\frac {e^{i(\omega _{kg}+\omega )t}-1}{\omega _{kg}+\omega }}+{\frac {e^{i(\omega _{kg}-\omega )t}-1}{\omega _{kg}-\omega }}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d5e4872c67deeb9e95cc30b7f74ecd1122ce0f)



![{\displaystyle {\begin{array}{rcl}\langle D(\omega ,t)\rangle &=&2{\rm {Re}}{\left\{\langle g|{\bf {D}}|\sum _{k}a_{k}^{(1)}(t)e^{-i\omega _{kg}}|k\rangle \right\}}\\&=&{\mathcal {E}}{\rm {Re}}{\left[\sum _{k}{\frac {\langle g|D|k\rangle \langle k|{\hat {e}}\cdot D|g\rangle }{\hbar }}{\left\{{\frac {e^{i\omega t}}{\omega _{kg}+\omega }}+{\frac {e^{-i\omega t}}{\omega _{kg}-\omega }}\right\}}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bd4119db9415e85baec8331b26488d24624bfc)























![{\displaystyle [A,B^{2}]=[A,B]B+B[A,B],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e16bcf41c2c00f41091a8b2f6ec1a54c3c26aa3)
![{\displaystyle [r_{j},p_{k}]=i\hbar \delta _{jk}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47639ff8ac69b050c5dc9d8cf58f9c6d17af6a3)
![{\displaystyle [r,H]={\frac {i\hbar }{m}}p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/335156c1e95f556b5ff6979d61bd8c1ef0ea7263)


![{\displaystyle \langle j|[r,H]|k\rangle =(E_{k}-E_{n})\langle j|r|k\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4756f9f0266fc68ae7c3ce2a7995ae930e09add7)




![{\displaystyle \sum _{k}f_{kj}={\frac {i}{\hbar }}{\left[\langle j|p_{z}z-zp_{z}|j\rangle \right]}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9256c4cbcfdc8f1d87d37c52474b7279a2ec1990)
























![{\displaystyle -{\frac {\Gamma }{2\delta }}\rightarrow {\frac {\Gamma }{\gamma }}{\bigg (}{\frac {-1}{\delta '+i}}{\bigg )}={\frac {\Gamma }{\gamma }}{\bigg [}{\frac {i}{1+\delta '^{2}}}-{\frac {\delta '}{1+\delta '^{2}}}{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb78543c9cc15115ec953d0e8e9cd07c77f655be)
![{\displaystyle e^{ikz}=e^{in_{r}{\frac {\omega }{c}}z}=e^{-{\frac {D_{0}}{2}}[{\frac {1}{1+\delta '^{2}}}-{\frac {i\delta '}{1+\delta '^{2}}}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72317571d524b12432dc20f8849a006278731164)




