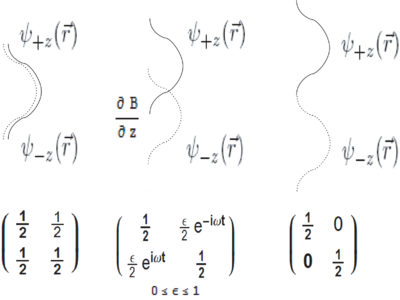Coherence

donewcmd error! no pattern match \newcommand{\QU}[1]{\par%

Coherence

We speak of coherence if there exist well defined phases between two or more amplitudes that can interfere. These can be, e.g., the relative phase of the electric field in two arms of an interferometer, the relative phase of two or more states within one atom, or the relative phase of oscillating dipole moments in different atoms. Coherence is often a measurement tool in that the relative phase is the time integral over the energy difference between the states. For instance, if the atomic states have different magnetic moments, coherence between them provides a very sensitive measurement tool for magnetic field, or if the states have different spatial wavefunctions, the relative phase is a sensitive measure of the gravitational energy difference. In atomic clocks, coherence allows one to transform as energy difference between two internal atomic states into a frequency and time standard.

Coherence in two-level systems

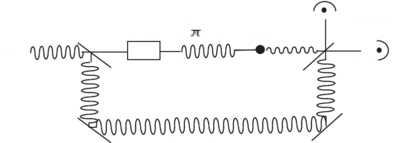
A two-level atom that has been prepared by a ${\frac {\pi }{2}}$ pulse in a superposition ${\frac {1}{\sqrt {2}}}(|g\rangle +|e\rangle )$ can be viewed as exhibiting coherence, since the phase between $|e\rangle$ and $|g\rangle$ is well defined, and the system will evolve coherently as ${\frac {1}{\sqrt {2}}}(|g\rangle +e^{-i\omega _{o}t}|e\rangle )$ for times $t\leq {\frac {1}{\Gamma }}$, where $\Gamma$ is the decay rate constant for the excited state. Figure \ref{fig:single-atom-coherence} displays a conceptual experiment that can be used to test this. \begin{figure} \centering

\caption{Measurement of definite phase for light emitted by a two-level atom prepared with a $\pi /2$ pulse. The laser light is sent through both arms of an interferometer; a switch in one arm selects a $\pi /2$ pulse of light from the laser with which to excite the atom. The light the atomic dipole emits is then mixed with the other interferometer arm at the output. Averaging the output signal over many repetitions of the experiment, the interferometer measures a definite phase for the light emitted by the atom, defined relative to the phase of the exciting $\pi /2$ pulse.}

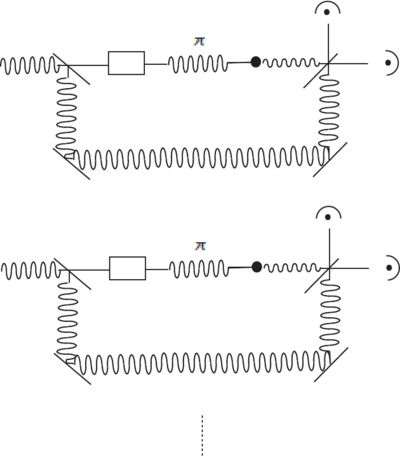
\end{figure} What about an atom prepared by a $\pi$ pulse in $|e\rangle$? There is no coherence at $t=0$, since the atom is in a single state, but what about $t={\frac {1}{\frac {\Gamma }{2}}}$? Then the atom is in a superposition of states $\sim |g\rangle +e^{-i\omega _{0}t+\phi _{0}}|e\rangle$. Obviously some phase must exist, because otherwise no dipole moment ${\bf {d}}(t)=\langle e(t)|q{\bf {r}}|g(t)\rangle$ exists that can emit ($\int _{0}^{2\pi }d\phi \langle e|e^{i\phi }q{\bf {r}}|g\rangle =0$), but the phase $\phi _{0}$ is completely unpredictable, so the experiment pictured above (or an emsemble average, as in Figure \ref{fig:ensemble-average-coherence}) would yield no definite phase. We conclude that an atom prepared in $|e\rangle$ does not exhibit coherence. \begin{figure} \centering

\caption{Ensemble average of the phase measurement.}

\end{figure} The ensemble average (parallel setups) or time average (repeated experiment at same location) yields no definite phase, so we conclude that the expectation value of the dipole moment $\langle d(t)\rangle =0$ is zero at all times. What is the origin of uncertain phase $\phi _{o}$? Vacuum fluctuations. What then happens if we place two atoms close together and excite them at the same time? Is the relative phase of the evolving dipole moments fixed or uncertain? If the relative phase is fixed, how close must the atoms be for the relative phase to be well defined? These questions about spatial coherence and Dicke superradiance will be covered later in the chapter.

Precession of a spin in a magnetic field

Precession of a spin can be viewed as an effect of coherence since $|x\rangle ={\frac {1}{\sqrt {2}}}(|+z\rangle +|-z\rangle )$. In a magnetic field $|\psi (t)\rangle ={\frac {1}{\sqrt {2}}}(e^{-i\omega _{L}{\frac {t}{2}}}|+z\rangle +e^{i\omega _{L}{\frac {t}{2}}}|-z\rangle )$, so the precession is due to a coherence between the $|\pm z\rangle$ components of the spin. If no coherence existed, the spin would be in a statistical mixture of $|+z\rangle$ and $|-z\rangle$. In the density matrix formalism,

$\rho =\left({\begin{array}{cc}{\frac {1}{2}}&{\frac {1}{2}}e^{-i\omega _{L}t}\\{\frac {1}{2}}e^{i\omega _{L}t}&{\frac {1}{2}}\\\end{array}}\right)$

in the z basis $|+z\rangle =\left({\begin{array}{cc}1\\0\end{array}}\right),|-z\rangle =\left({\begin{array}{cc}0\\1\end{array}}\right)$.\\The expectation value of ${\hat {\sigma }}_{x}=\left({\begin{array}{cc}0&1\\1&0\end{array}}\right)$,

$\langle {\hat {\sigma }}_{x}\rangle =Tr[\rho {\hat {\sigma }}_{x}]=Tr\left({\begin{array}{cc}{\frac {1}{2}}e^{-i\omega _{L}t}&{\frac {1}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}e^{i\omega _{L}t}\end{array}}\right)=\cos \omega _{L}t.$

If the coherences (off-diagonal elements of ${\hat {\rho }}$) were smaller, ${\hat {\sigma }}_{x}$ would be smaller. For a statistical mixture of $|+z\rangle$ and $|-z\rangle$, $\rho =\left({\begin{array}{cc}{\frac {1}{2}}&0\\0&{\frac {1}{2}}\end{array}}\right)$ and $\langle {\hat {\sigma }}_{x}\rangle =0$.

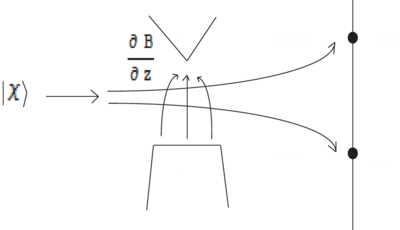
The Stern-Gerlach experiment and spatial loss of coherence

\begin{figure} \centering

\caption{Stern-Gerlach experiment. Where in the magnet (or outside) does the projection onto $|\pm z\rangle$ occur?} \end{figure} In the Stern-Gerlach experiment a particle initially spin-polarized along $|x\rangle$ has equal probability of following either the $|+z\rangle$ trajectory or the $|-z\rangle$ trajectory. So initially the particle is described by a density matrix for a pure state,

$\rho _{in}=\left({\begin{array}{cc}{\frac {1}{2}}&{\frac {1}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}\end{array}}\right),$

after passing the Stern-Gerlach apparatus (inhomogeneous magnetic field) the density matrix is

$\rho _{out}=\left({\begin{array}{cc}{\frac {1}{2}}&0\\0&{\frac {1}{2}}\end{array}}\right)$

with no intereference possible between the two states. Why? Because describing the full quantum state of the particle also requires acocunting for its spatial wavefunction. The density matrix above does not contain all the relevant degrees of freedom. Correctly, the particle should initially be described by

$|\psi \rangle =|x\rangle \otimes |\psi _{spat}\rangle ={\frac {1}{\sqrt {2}}}\left({\begin{array}{c}\psi _{in}({\bf {r}})\\\psi _{in}({\bf {r}})\end{array}}\right)$

with $\psi _{+z}({\bf {r}})=\psi _{-z}({\bf {r}})=\psi _{in}({\bf {r}})$, i.e. a spatial wavefunction independent of internal state, $\rho _{in}=\rho _{in,spin}\otimes \rho _{in,spatial}$. In the inhomogeneous magnetic field, the wavefuntion components $\psi _{+z},\psi _{-z}$ evolve differently because there is a different potential energy seen by the two spin states $|\pm z\rangle$:

$|\psi (t)\rangle ={\frac {1}{\sqrt {2}}}\left({\begin{array}{c}\psi _{+z}({\bf {r}},t)\\\psi _{-z}({\bf {r}},t)\end{array}}\right).$

\begin{figure} \centering

\caption{Spatial wave function and corresponding spin density matrix in the Stern-Gerlach experiment.} \end{figure} The coherence (interference) between $|+z\rangle$ and $|-z\rangle$ components to form $|x\rangle$ exists only in the region where there is at least partial overlap between the two wavefunctions $\psi _{+z}({\bf {r}}),\psi _{-z}({\bf {r}})$. When the wavefunctions do not overlap, there is no significance to a relative phase between $|+z\rangle$ and $|-z\rangle$, i.e. no interference term. (Of course, if the wavefunctions are steered back to overlap, we can ask if there was a well-defined relative phase between them while they were separated.) In a more complete description, the inhomogeneous magnetic field entangles the spatial and spin degrees of freedom. When the spatial overlap disappears, or equivalently, when we trace over the spatial wavefunction (by measuring the particle either at location 1 or at location 2), the interference between $|+z\rangle$ and $|-z\rangle$ giving rise to $|x\rangle$ disappears. In a measurement language, the inhomogeneous magnetic field entangles the "variable" ($|\pm z\rangle$) with the "meter" (the spatial wavefunctions of the particle). Once the spatial wavefunctions $\psi _{+z}({\bf {r}}),\psi _{-z}({\bf {r}})$ cease to overlap, the particle's position can serve as a "meter" for the variable to be measured, the spin along $\pm z$. However, until the particle hits the screen, or is subjected to uncontrolled or unknown magnetic fields, the meter-variable entanglement is still reversible, and a "measurement" has not been made.

Quantum Beats

Quantum beats can be thought of as a two-level effect, though they are observed in multilevel atoms. They allow one to measure level spacings with high resolution when a narrowband excitation source (narrowband laser) is not available. \begin{figure} \centering

\caption{Multiple levels within energy $\hbar \Delta$ from ground state, $\Delta >\Gamma ,\Gamma '$,\ldots}

\end{figure} Consider the scenario of Figure \ref{fig:qb-levels}, where we have multiple excited levels in a narrow energy interval $\hbar \Delta$, all decaying to a common ground state. If we excite with a pulse of duration $\Delta t\ll {\frac {1}{\Delta }}$, we cannot resolve the levels, and they will be populated according to the coupling strength to the ground state $|g\rangle$ for the given excitation method:

$|\psi (0)\rangle =\Sigma c_{i}|e^{(i)}\rangle$

and for times $t\ll {\frac {1}{\Gamma }},{\frac {1}{\Gamma '}},{\frac {1}{\Gamma ''}},\ldots$, the state vector is

$|\psi (t)\rangle =\Sigma c_{i}e^{-i\omega _{i}t}|e^{(i)}\rangle .$

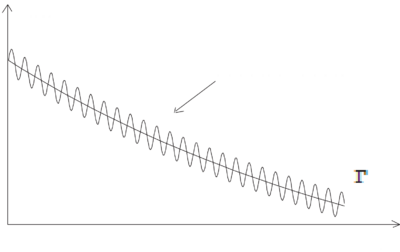
It follows that, in directions where the radiation from the levels $|e^{(i)}\rangle$ interferes, there will be oscillating terms at frequencies $\omega _{i}-\omega _{j}$ on top of the excited state decay. \begin{figure} \centering

\caption{Quantum beats}

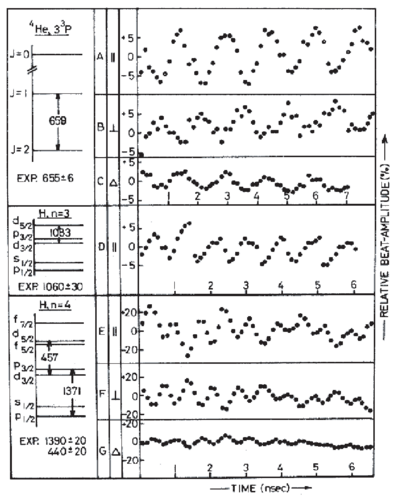
\end{figure} This allows one to measure excited-state splittings in spite of the lack of a sufficiently narrow excitation source. Compared to our initial example of a two-level atom, here the coherence is initially purely between the excited states (definite excitation phase between them), and no coherence between $|e^{(i)}\rangle$ and $|g\rangle$ exists initially. Of course, as the atom decays, coherence between $|e^{(i)}\rangle$ and $|g\rangle$ (e.g. dipole moments) build up, and the coherence between the emitted fields of the different dipoles gives rise to the observed effect. Figures \ref{fig:qb-ideal} and \ref{fig:qb-data} show respectively an idealized quantum beat signal and real data from an experimental demonstration of the technique. \begin{figure} \centering

\caption{Schematic level diagrams and observed quantum beats of $^{4}He3^{3}P$ at 475 keV/atom; H, n=3, and H, n=4 at 133 keV/atom. \cite{Andra1970}}

\end{figure} \putbib