Difference between revisions of "Magneto-Optical Traps"
imported>Ichuang |
imported>Ichuang |
||
| Line 100: | Line 100: | ||
<math>k</math> and the field gradient strenght <math>\beta</math>, | <math>k</math> and the field gradient strenght <math>\beta</math>, | ||
:<math> | :<math> | ||
| − | \omega_{\rm trap} | + | \omega_{\rm trap} \propto \frac{\beta}{k} |
\,. | \,. | ||
</math> | </math> | ||
Revision as of 22:57, 15 April 2009
The Magneto-Optical Trap (MOT) is a configuration of atoms in laser cooling beams and coils producing static magnetic fields, which is astonishingly effective in cooling atoms from room temperature to microkelvin scale temperatures. Today, the MOT is a workhorse of atomic physics, and the starting point for many atomic physics experiments, such as with Bose-Einstein condensates.
We begin our study of the MOT with an explanation of how it was originally thought to be impossible, due to the optical Earnshaw theorem. We then present the physics of two-level atoms in a one-dimensional MOT, from which generalization to 3D MOT's trapping real multi-level atoms is straightforward.
Contents
Optical Earnshaw Theorem
Some history helps place the MOT in context. In the 1970's and 1980's, many people discussed prospects for, and limitations of the stimulated and spontaneous force. In 1983, Gordon and Ashkin derived the optical Earnshaw theorem. The (standard, electromagnetic) Earnshaw theorem states that a charged particle will never be in a stable equilibrium in a static, 3D configuration of electric fields. This holds because for a particle to be stable, all field lines must point inwards, but we know that the divergence of the electric field in vacuum is zero.
The optical Earnshaw theorem states, in a similar way, that a 3D sponteneous light force trap is not possible. This was not a very positive start for atom trapping. The proof goes as follows. Recall that the sponeaneous light force is related to the Poynting vector as
where is the Poynting vector. From electromagnetism, however, we know that
but we know that if there is zero local energy density . This contradicts the requirement that .
Where is the flaw in this reasoning? In 1986, David Pritchard realized there were many ways to circumvent the optical Earnshaw theorem. What is ignored here is the {\em internal structure of the atom}. After all, the spontaneous light force is actually not just proportional to the incident light flux. The assumption that every atom which is exposed to the same Poynting vector experiences the same force, is just wrong. Namely,
The force can thus be spatially dependent. First, can experience saturation. Second, optical pumping can be used, taking advantage of internal structure of the atoms. Third, there can be line shifts due to external static fields, as when hyperfine states are used which are magnetic field sensitive.
The perfect solution was demonstrated in 1987, in a collaboration between MIT (paper by Raab et al) and Steve Chu's group at Bell Labs.
1-dimensional MOT
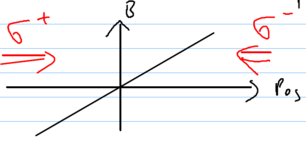
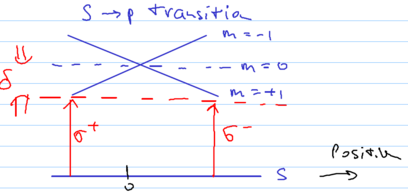
Consider two counterpropagating laser beams with opposite circular polarizations, incident on some atoms, in the presence of a static magnetic field gradient:
The energy levels of three hyperfine levels, with and , become a function of space due to the magnetic field, so that the and polarized light beams interact with spatially localized classes of atoms:
This scenario is similar to an optical molasses, but the frequency shifts are due to a magnetic field gradient . Just as in the molasses analysis, we must add the effects of the left and right laser beams. Assume we have low intensity, so we find that
For small , ,
The equation of motion for the atom is thus that of a harmonic oscillator, because the force is linear with displacement:
where the trap frequency is given by the ratio of the light momentum and the field gradient strenght ,
Typically, experimental parameters lead this to be an overdamped harmonic oscillator, with kHz, and a damping time of about s. The static well depth is usually around a few Kelvin, but the dynamic depth is even larger. The dynamic depth refers to how much kinetic energy an atom can get before it is recaptured by the trap, because it is cooled by optical molasses effects even after it leaves the local potential well.
3D MOT trapping with real atoms
Real atoms have a multilevel structure, with complicated hyperfine structure. If you have a complicated ground state structure, you need to include optical pumping effects between all the levels, but the combination of these effects and the simple Zeeman shift model discussed above works very well.
Recall that optical molasses works better than originally anticipated, in which it was found that the damping due to polarization gradients was much much larger than the damping due to doppler cooling, The same turns out to be true for the restoring force in magneto-optical traps.
We have discussed only the 1D scheme above. You may not appreciate it, but a lot of spontaneous light forces which were discussed to circumvent the optical Earnshaw theorem worked in 1D, but were very difficult to generalize to 3D. The MOT scheme, on the other hand, generalizes very well to 3D. By using three pairs of anti-Helmholtz coils to create the field gradients, and six laser beams, you get the generalizeation to 3D and it works as well as in one dimension.
Example: vapor cell MOT
Consider a cesium vapor cell MOT. The atoms, initially at 300K, can be cooled to K. The density starts at cm, which is increased to cm. This means that the phase space density, which is , has been increased by order of magnitude. Initially, the phase space density before cooling is orders magnitide away from Bose-Einstein condensation; after MOT trapping, the system is much closer - only order of magnitude closer, but not yet there.














![{\displaystyle F=F_{R}+F_{L}={\frac {\hbar k\Gamma }{2}}\left[{\frac {I/I_{0}}{1+4\left({\frac {\delta -kv-\beta z}{\Gamma }}^{2}\right)}}-\cdots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4f0102122f519911fc0f78cded6f0d0f094239)


![{\displaystyle F(v,z)={\frac {\hbar k\Gamma }{2}}\left[-kv-\beta z\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf931fc215e9c18a397895ee24334ac6d33b5792)
















