Difference between revisions of "Casimir interaction"
imported>Wikibot m (New page: === Semiclassical derivation of the Casimir force === Today, we will look at a completely different derivation of the Casimir force, based on zero-point fluctuations. Our goal will be to...) |
imported>Ichuang |
||
| Line 1: | Line 1: | ||
| + | <categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;" hideprefix=auto>8.422</categorytree> | ||
| + | |||
=== Semiclassical derivation of the Casimir force === | === Semiclassical derivation of the Casimir force === | ||
| Line 131: | Line 133: | ||
able to well approximate the resulting force as being independent of | able to well approximate the resulting force as being independent of | ||
atomic properties. | atomic properties. | ||
| + | |||
| + | === References === | ||
| + | |||
| + | [[Category:Photon-atom interactions]] | ||
Revision as of 14:06, 10 April 2009
Semiclassical derivation of the Casimir force
Today, we will look at a completely different derivation of the Casimir force, based on zero-point fluctuations. Our goal will be to discus the origin of the Casimir force, whether is a result of photon exchange, or something else.
Virtually all of what we will see from the Casimir force is that it can be understood via classical fields between two conducting plates. Once we have all the electromagnetic modes, we can multiply each by then sum to get the zero point energy of the field. We will follow a derivation given by Haroche (Les Houches summer school), and additional discussion comes from Jackson.
Consider two parallel metallic plates, separated by distance . Due to the boundary condition that the field must be zero at and , where describes a point between the plates, we have a discrete set of modes perpendicular to the plates. Specifically, the TE and TM modes are:
Parallel to the plates, we have propagating modes which can assume all the usual parameter values for free space propagation.
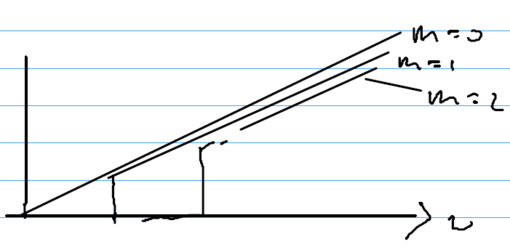
We want to count these modes, and obtain the density of states. Consider the number of modes with momentum between and . In a waveguide, the total wavenumber is . Thus, for each standing wave, there is a continuum, with wavenumber starting at the base value given by the standing wave, and increasing continuously from there. Ths means that the density of modes for a given mode number (the standing wave index for the modes perpendicular to the plates) is, using the fact that is proportional to :
In two dimensions the mode density is linear, and in three dimensions it is parabolic. In this model with the plates, there are discrete steps, in comparison to the free space case. More analytically, we find
We can now use these expressions to get the total zero point energy in volume . We get
The integrand diverges, which is unphysical. In reality, a high frequency cutoff needs to be introduced, particularly because we will want to compare the effect of two different boundary conditions on the zero point energy, so we will be subtracting two integrals. Adding such a cutoff term , we find
with
Note
This can be expanded about , where , corresponding to letting .
We want to compare mode densities, so let us embed our capacitor of spacing within a bigger capacitor of spacing . We compute , and drop terms independent of . This gives
This gives the Casimir potential,
The Casimir force, given as a pressure betwen the two plates, is thus
Such a derivation can also be done for models other than two metallic plates. You can also derive in the same way the Casimir potential for a metal plate interacting with a single atom. This is done by recognizing that the atom is a dielectric medium, which modifies the field density near the metal plate. Similarly, for the atom-atom interaction, the two atoms can be put inside a large box; the two atoms act as tiny dielectric media, which change the field density in the box, also leading to a Casimiar potential.
Interpretation of the Casimir Potential
The interpretation of the Casimiar potential has become quite interesting recently because of the realization that the origin of dark matter may arise from the physical reality of zero point energy. Such zero point energy could concievably give rise to a gravitational force. However, the numerical value of the potential strength obtained is hundreds of orders of magnitude off from what would be needed to be consistent with the observed value of the cosmological constant. Nevertheless, there is much to be learned from the different derivations of the Casimiar force.
Let us discuss the two derivations we've seen. One way was to use two metallic plates and to count the number of modes inbetween them. Another way was to consider all the atoms in two parallel walls, and allow the atoms to exchange virtual photons. Robert Jaffe has written a beautiful treatise (Phys. Rev. D) discussing these two viewpoints, and shows these are equivalent, and that one does not even need, in principle, the concept of zero point energies. The conclision is that you should not use the existence of the Casimir force as evidence of zero point energy.
Note that the Casimir force is independent of atomic properties, in the limit that the fine structure constant is very large. If you take the limit , then the atomic radius , in which case the Casimir force also goes to zero. Thus, by taking our material to be metallic, we are assuming that the fine structure constant is large. For distances as small as m, it is sufficient for to be able to well approximate the resulting force as being independent of atomic properties.





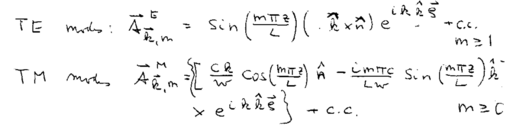





![{\displaystyle {\begin{array}{rcl}\rho (\omega )d\omega ={\frac {a^{2}}{2\pi c^{2}}}\left[{1+2...}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef3194a8f0d72773ed2c540091d11d536be3f310)

![{\displaystyle {\begin{aligned}W(L)&=\int _{0}^{\infty }{\frac {\hbar \omega }{2}}\rho (\omega )d\omega \\&={\frac {a^{2}\hbar }{4\pi c^{2}}}\left[{\int _{0}^{\infty }\omega ^{2}d\omega +2\sum _{m=1}^{\infty }\int _{m\pi c/L}^{\infty }\omega ^{2}d\omega }\right]\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdac3bf637c4c48f14709650136e42756e5526a5)



![{\displaystyle {\begin{array}{rcl}\sum _{m}I_{m}={\frac {c^{3}\pi }{L}}{\frac {\partial ^{2}}{\partial \lambda ^{2}}}\left[{{\frac {1}{(\pi \lambda /L)}}{\frac {1}{e^{\pi \Lambda /L}-1}}}\right]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1028f463088a7c7c3c4378e7cd45286d958f80fe)













