Difference between revisions of "Techniques for cooling to ultralow temperatures"
imported>Ichuang |
imported>Wikibot m |
||
| Line 7: | Line 7: | ||
1980's was magnetic cooling and trapping, including work by Phillips, | 1980's was magnetic cooling and trapping, including work by Phillips, | ||
Pritchard, and Greytak, on sodium and other atoms. | Pritchard, and Greytak, on sodium and other atoms. | ||
| + | |||
| + | === Earnshaw theorem === | ||
| + | |||
Recall the Earnshaw theorem, previously discussed for the optical | Recall the Earnshaw theorem, previously discussed for the optical | ||
force, and for trapped ions. This states that trapping requires <math> \nabla | force, and for trapped ions. This states that trapping requires <math> \nabla | ||
| Line 19: | Line 22: | ||
at rest in free space in static electric fields. The same theorem | at rest in free space in static electric fields. The same theorem | ||
applies for magnetic multipole distributions. | applies for magnetic multipole distributions. | ||
| + | |||
| + | ==== Circumventing the Earnshaw theorem ==== | ||
Sir James-Jeans, in 1925, pointed out a way around this limit. If the | Sir James-Jeans, in 1925, pointed out a way around this limit. If the | ||
matter is polarizible, this can change the electric fields. | matter is polarizible, this can change the electric fields. | ||
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures- | + | |
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra1.png|thumb|400px|none|]] | ||
| + | |||
The displacement of the trapped particle or of the field | The displacement of the trapped particle or of the field | ||
generated by a particle which are energetically favorable are | generated by a particle which are energetically favorable are | ||
forbidden due to constraints. This leads to a loophole, as | forbidden due to constraints. This leads to a loophole, as | ||
exemplified by magnet stabilized above a superconductor: | exemplified by magnet stabilized above a superconductor: | ||
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures- | + | |
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra2.png|thumb|400px|none|]] | ||
| + | |||
The constraint that no magnetic field may enter a superconducot causes | The constraint that no magnetic field may enter a superconducot causes | ||
shielding currents to be created which stabilize the trapping | shielding currents to be created which stabilize the trapping | ||
configuraiton for the levitated particle. This happens in a | configuraiton for the levitated particle. This happens in a | ||
configuration which is not a minimum of the magnetic energies. | configuration which is not a minimum of the magnetic energies. | ||
| + | |||
Of course, electronic feedback can be used to create a stable trapping | Of course, electronic feedback can be used to create a stable trapping | ||
potential, providing time varying fields. | potential, providing time varying fields. | ||
| − | Another | + | Another example is provided by diamagnetic matter. Such matter expels |
an external field. | an external field. | ||
| − | + | Yet another, important, example is if <math>\vec{\mu}\cdot\vec{B}</math> is | |
| − | constrains angular momentum; the dipole moment is not allowed to flip | + | constant. This constrains angular momentum; the dipole moment is not |
| − | over to move into what might be a more energetically favorable | + | allowed to flip over to move into what might be a more energetically |
| − | + | favorable configuration. | |
| + | |||
| + | === Trapping a magnetic moment === | ||
| + | |||
| + | Now let us see how these ideas can allow trapping of an object with a | ||
| + | magnetic moment. Let us consider when a magnetic moment might be | ||
| + | constrained such that the potential depends only on the absolute value | ||
| + | of the magnetic field, <math>U\sim |\vec{B}|</math>. | ||
| + | |||
| + | ==== Wing's theorem ==== | ||
| − | |||
| − | |||
| − | |||
Wing's theorem (1983) says that in a region dvoid of charges and | Wing's theorem (1983) says that in a region dvoid of charges and | ||
currents, quasistatic electric of magnetic fields can have local | currents, quasistatic electric of magnetic fields can have local | ||
| Line 64: | Line 80: | ||
because of the <math>(\delta \vec{E}(r))^2</math> term. There can thus be local | because of the <math>(\delta \vec{E}(r))^2</math> term. There can thus be local | ||
minima, but not local maxima, in an electric field configuration. | minima, but not local maxima, in an electric field configuration. | ||
| + | |||
By Wing's theorem, since there can only be local minima (and not | By Wing's theorem, since there can only be local minima (and not | ||
maxima) in a static magnetic field, to have a stable magnetic trap, | maxima) in a static magnetic field, to have a stable magnetic trap, | ||
| Line 71: | Line 88: | ||
momenta changes of atomic motion), and Majorana flops. | momenta changes of atomic motion), and Majorana flops. | ||
| − | More specifically, <math>\vec{\mu}</math> must be antiparallel to <math>\vec{B}</math> only | + | ==== Classical magnetic moment in a trap ==== |
| − | adiabatically, as follows. Consider the problem of trapping a | + | |
| − | classical magnetic moment. Such a magnetic moment precesses in a | + | More specifically, to trap, <math>\vec{\mu}</math> must be antiparallel to |
| − | magnetic field: | + | <math>\vec{B}</math> only adiabatically, as follows. Consider the problem of |
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures- | + | trapping a classical magnetic moment. Such a magnetic moment |
| + | precesses in a magnetic field: | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra3.png|thumb|400px|none|]] | ||
What is needed is for the precession of the magnetic moment to follow | What is needed is for the precession of the magnetic moment to follow | ||
| Line 84: | Line 104: | ||
:<math> | :<math> | ||
\omega_{rot} = \frac{d\theta}{dt} \ll \frac{U_i-U_j}{\hbar} = | \omega_{rot} = \frac{d\theta}{dt} \ll \frac{U_i-U_j}{\hbar} = | ||
| − | \frac{g\mu_B B}{\ | + | \frac{g\mu_B B}{\hbar} = \omega_{larmor} |
\,. | \,. | ||
</math> | </math> | ||
| + | |||
In the spherical quadrupole magnetic trap, made by anti-Helmholz | In the spherical quadrupole magnetic trap, made by anti-Helmholz | ||
coils, spins can flip in the following way, known as Majorana flops. | coils, spins can flip in the following way, known as Majorana flops. | ||
As an atom moves through the field configuration: | As an atom moves through the field configuration: | ||
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-|thumb| | + | |
| − | + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra4.png|thumb|510px|none|]] | |
| + | |||
it should flip its moment as it moves through the center of the field; | it should flip its moment as it moves through the center of the field; | ||
however, there is a zero in the field at the center, at which point | however, there is a zero in the field at the center, at which point | ||
the spin can easily find itself aligned parallel with the field upon | the spin can easily find itself aligned parallel with the field upon | ||
the atom's exit. This causes atoms to leak from the trap. | the atom's exit. This causes atoms to leak from the trap. | ||
| − | + | ||
| + | ==== Levitron example ==== | ||
| + | |||
| + | Levitron movie | ||
Counterintuitively, spining the top faster does not lead to a more | Counterintuitively, spining the top faster does not lead to a more | ||
| Line 102: | Line 127: | ||
a process we may think of as being a classical analog of Majorana | a process we may think of as being a classical analog of Majorana | ||
flops. | flops. | ||
| + | |||
The levitron works in the following way. At <math>r=0</math>, | The levitron works in the following way. At <math>r=0</math>, | ||
:<math> | :<math> | ||
| − | B(z) = B_0 + B' z + B | + | B(z) = B_0 + B' z + B" z^2/2 |
</math> | </math> | ||
etc. | etc. | ||
The magnetic field above the center of the spinning magnet is thus | The magnetic field above the center of the spinning magnet is thus | ||
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures- | + | |
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra5.png|thumb|400px|none|]] | ||
| + | |||
The second derviative of the magnetic field must give positive | The second derviative of the magnetic field must give positive | ||
curvature along both the radial and axial directions, for the trap to | curvature along both the radial and axial directions, for the trap to | ||
| Line 130: | Line 158: | ||
The quantum equivalent of this scenario is reduction of the <math>g</math> | The quantum equivalent of this scenario is reduction of the <math>g</math> | ||
factor: spining the magnet faster corresponds to reduction of <math>g</math>. | factor: spining the magnet faster corresponds to reduction of <math>g</math>. | ||
| + | |||
| + | === Magnetic traps === | ||
| + | |||
In magnetic traps, <math>U = \mu_B B g m_F</math>. <math>B</math> can only have local | In magnetic traps, <math>U = \mu_B B g m_F</math>. <math>B</math> can only have local | ||
minima, and not maxima, so we must ensure the angle <math>\theta</math> of the | minima, and not maxima, so we must ensure the angle <math>\theta</math> of the | ||
field is such that the prefactors are positive. For Rubidium, we have | field is such that the prefactors are positive. For Rubidium, we have | ||
these energy level depenencies on the field: | these energy level depenencies on the field: | ||
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures- | + | |
| − | + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra6.png|thumb|400px|none|]] | |
| + | |||
The only states which are trapped are thus which have positive energy | The only states which are trapped are thus which have positive energy | ||
| − | versus magnetic field | + | versus magnetic field slopw. |
The spherical quadrupole trap has a linear field dependency versus | The spherical quadrupole trap has a linear field dependency versus | ||
postiion going through the center: | postiion going through the center: | ||
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures- | + | |
| − | + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra7.png|thumb|400px|none|]] | |
| + | |||
A plug is thus needed to close the <math>B=0</math> hole at <math>\vec{r}=0</math>. Two | A plug is thus needed to close the <math>B=0</math> hole at <math>\vec{r}=0</math>. Two | ||
strategies are (1) to use a repulsive dipole force, or (2) use a | strategies are (1) to use a repulsive dipole force, or (2) use a | ||
| − | rapidly rotating magnetic field -- the TOP trap. | + | rapidly rotating magnetic field -- the TOP trap: |
| − | linear bias field to displace the origin of the trap, such that the | + | |
| − | time-average potential produces no zero in the magnetic field. The | + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra8.png|thumb|400px|none|]] |
| − | Ioffe-Pritchard trap does this, with a constant field and a curvature | + | |
| − | created by four "Ioffe" bars, adding to the two "Pinch" coils: | + | The TOP trap adds a linear bias field to displace the origin of the |
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures- | + | trap, such that the time-average potential produces no zero in the |
| − | The Ioffe bars create the quadrature | + | magnetic field. The Ioffe-Pritchard trap does this, with a constant |
| − | a linear field. | + | field and a curvature created by four "Ioffe" bars, adding to the |
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures- | + | two "Pinch" coils: |
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-|thumb|400px|none|]] | + | |
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-|thumb|400px|none|]] | + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra9.png|thumb|400px|none|]] |
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-|thumb|400px|none|]] | + | |
| − | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-|thumb|400px|none|]] | + | The Ioffe bars create the quadrature field, |
| + | :<math> | ||
| + | B_z(z) = B_0 + \frac{B"}{2} z^2 | ||
| + | \,, | ||
| + | </math> | ||
| + | and the pinch field creates | ||
| + | a linear field, | ||
| + | :<math> | ||
| + | B = \sqrt{B_z^2 + B_\rho^2} \approx B_0 + \frac{B"}{2} z^2 + | ||
| + | \frac{1}{2} \frac{{B'}^2}{B_0^2} (x^2+y^2) | ||
| + | \,, | ||
| + | </math> | ||
| + | where the last term on the right is recognized to be <math>B_\rho^2/2B_0</math>. | ||
| + | This configuration can be used with <math>B_0\neq 0</math>: | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra10.png|thumb|400px|none|]] | ||
| + | |||
| + | This is a photograph of coils typically used: | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ultra11.png|thumb|400px|none|]] | ||
| + | |||
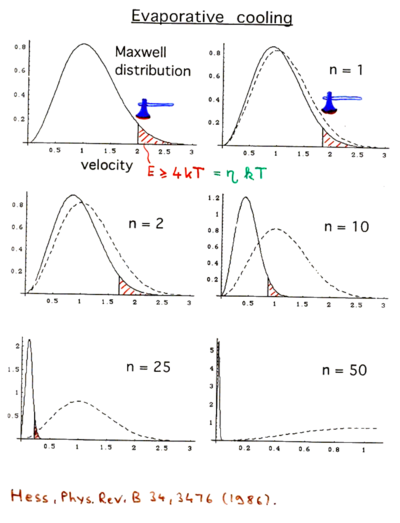
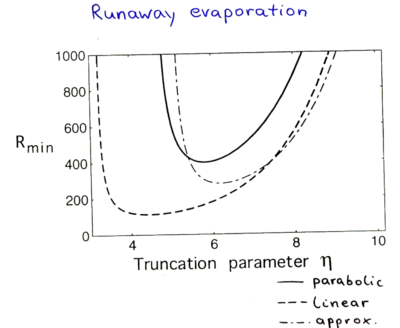
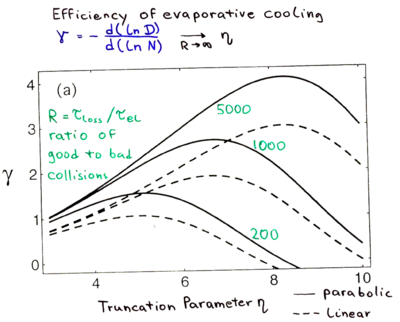
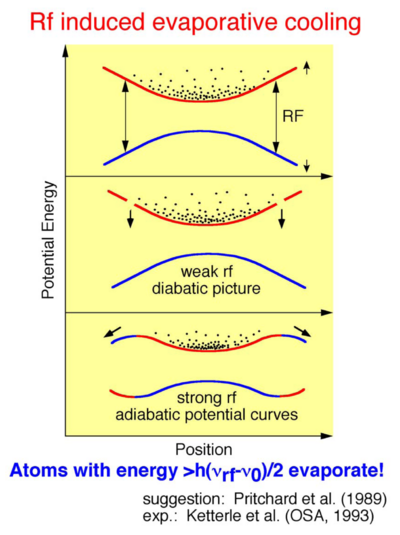
| + | == Evaporative cooling == | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool1.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool2.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool3.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool4.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool5.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool6.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool7.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool8.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool9.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool10.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool11.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool12.png|thumb|400px|none|]] | ||
| + | |||
| + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool13.png|thumb|400px|none|]] | ||
| − | + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool14.png|thumb|400px|none|]] | |
| − | [[ | + | ::[[Image:Techniques_for_cooling_to_ultralow_temperatures-ecool15.png|thumb|400px|none|]] |
Revision as of 15:20, 1 May 2009
Contents
Magnetic cooling
The principle of magnetic trapping is deflection by magnetic fields. This is at the heart of the Stern-Gerlach experiment in 1925. In the 1960's it was realized that magnetic confinement could be realized. It was first realized for neutrons, in 1978 by Paul. The exciting 1980's was magnetic cooling and trapping, including work by Phillips, Pritchard, and Greytak, on sodium and other atoms.
Earnshaw theorem
Recall the Earnshaw theorem, previously discussed for the optical force, and for trapped ions. This states that trapping requires or . For a rigid charge distribution, with positions , where is the center of mass motion and is the relative position of charge , we find that
must satisfy . An arbitrary rigid charge distribution (with arbitrary multiple moments) cannot be kept in stable equilibrium at rest in free space in static electric fields. The same theorem applies for magnetic multipole distributions.
Circumventing the Earnshaw theorem
Sir James-Jeans, in 1925, pointed out a way around this limit. If the matter is polarizible, this can change the electric fields.
The displacement of the trapped particle or of the field generated by a particle which are energetically favorable are forbidden due to constraints. This leads to a loophole, as exemplified by magnet stabilized above a superconductor:
The constraint that no magnetic field may enter a superconducot causes shielding currents to be created which stabilize the trapping configuraiton for the levitated particle. This happens in a configuration which is not a minimum of the magnetic energies.
Of course, electronic feedback can be used to create a stable trapping potential, providing time varying fields.
Another example is provided by diamagnetic matter. Such matter expels an external field.
Yet another, important, example is if is constant. This constrains angular momentum; the dipole moment is not allowed to flip over to move into what might be a more energetically favorable configuration.
Trapping a magnetic moment
Now let us see how these ideas can allow trapping of an object with a magnetic moment. Let us consider when a magnetic moment might be constrained such that the potential depends only on the absolute value of the magnetic field, .
Wing's theorem
Wing's theorem (1983) says that in a region dvoid of charges and currents, quasistatic electric of magnetic fields can have local minima, but not local maxima. The proof of this fact is by non-existence of a maximum by contradition. Assume is a max. Then
It follows that
and the cross-term must be always negative. Without loss of generality, this requires, for example, . However, that presents a contraditction with the Laplace equation (recall Earnshaw's theorem). A minimum, on the other hand, is possible because of the term. There can thus be local minima, but not local maxima, in an electric field configuration.
By Wing's theorem, since there can only be local minima (and not maxima) in a static magnetic field, to have a stable magnetic trap, must be antiparallel to . The limits to stability of magnetic traps include spin realaxation (inolving nuclear magnetic moment changes), dipolar relaxation (involving angular momenta changes of atomic motion), and Majorana flops.
Classical magnetic moment in a trap
More specifically, to trap, must be antiparallel to only adiabatically, as follows. Consider the problem of trapping a classical magnetic moment. Such a magnetic moment precesses in a magnetic field:
What is needed is for the precession of the magnetic moment to follow and maintain the same angle with respect to the field, as the moment moves in an inhomogeneous field. If the field changes slowly, the precession will follow the field, but if the field changes too rapidly, the spin may no longer be antiparallel with respect to the field:
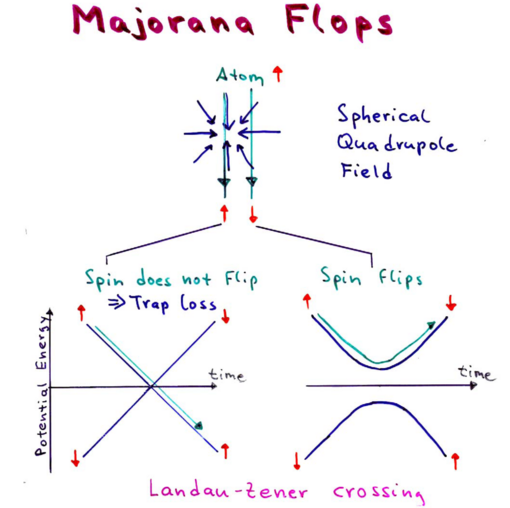
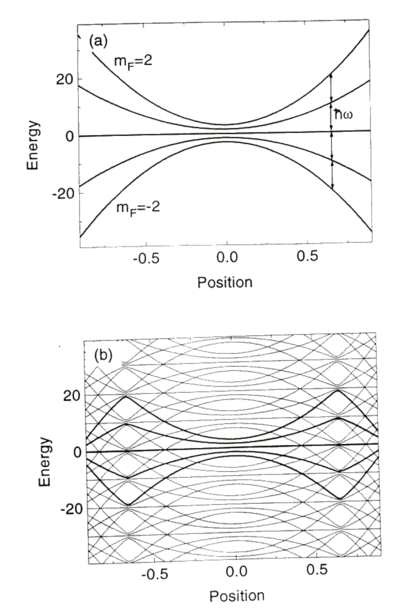
In the spherical quadrupole magnetic trap, made by anti-Helmholz coils, spins can flip in the following way, known as Majorana flops. As an atom moves through the field configuration:
it should flip its moment as it moves through the center of the field; however, there is a zero in the field at the center, at which point the spin can easily find itself aligned parallel with the field upon the atom's exit. This causes atoms to leak from the trap.
Levitron example
Levitron movie
Counterintuitively, spining the top faster does not lead to a more stable trap. Rather, it causes increased instability; this is due to a process we may think of as being a classical analog of Majorana flops.
The levitron works in the following way. At ,
- Failed to parse (syntax error): {\displaystyle B(z) = B_0 + B' z + B" z^2/2 }
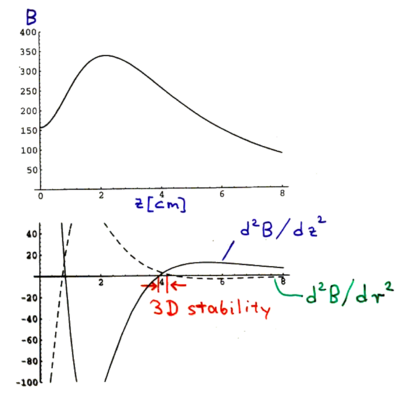
etc. The magnetic field above the center of the spinning magnet is thus
The second derviative of the magnetic field must give positive curvature along both the radial and axial directions, for the trap to be stable. This plot shows there is only a very small stability range for the trap.
Recall our trapping criterion: must stay anti-parallel to . This happens due to precession, as long as . The precession frequency of a gyroscope is given by the torque, so
where is the moment of intertia. is thus violated for large or . Around , one gets spin flips, referred to as Majorana flops in magnetic trapping of atoms.
The quantum equivalent of this scenario is reduction of the factor: spining the magnet faster corresponds to reduction of .
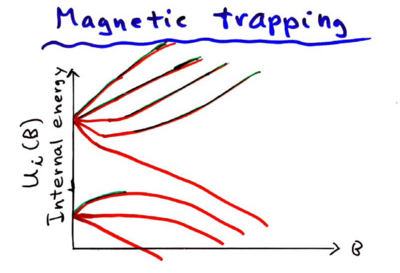
Magnetic traps
In magnetic traps, . can only have local minima, and not maxima, so we must ensure the angle of the field is such that the prefactors are positive. For Rubidium, we have these energy level depenencies on the field:
The only states which are trapped are thus which have positive energy versus magnetic field slopw.
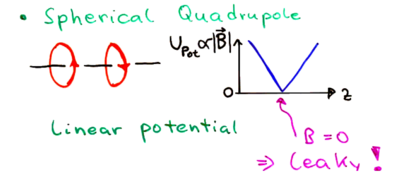
The spherical quadrupole trap has a linear field dependency versus postiion going through the center:
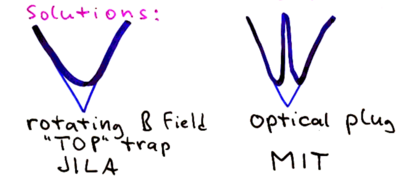
A plug is thus needed to close the hole at . Two strategies are (1) to use a repulsive dipole force, or (2) use a rapidly rotating magnetic field -- the TOP trap:
The TOP trap adds a linear bias field to displace the origin of the trap, such that the time-average potential produces no zero in the magnetic field. The Ioffe-Pritchard trap does this, with a constant field and a curvature created by four "Ioffe" bars, adding to the two "Pinch" coils:
The Ioffe bars create the quadrature field,
- Failed to parse (syntax error): {\displaystyle B_z(z) = B_0 + \frac{B"}{2} z^2 \,, }
and the pinch field creates a linear field,
- Failed to parse (syntax error): {\displaystyle B = \sqrt{B_z^2 + B_\rho^2} \approx B_0 + \frac{B"}{2} z^2 + \frac{1}{2} \frac{{B'}^2}{B_0^2} (x^2+y^2) \,, }
where the last term on the right is recognized to be . This configuration can be used with :
This is a photograph of coils typically used: