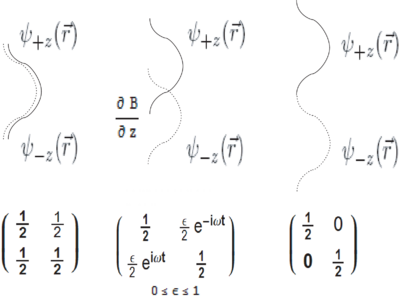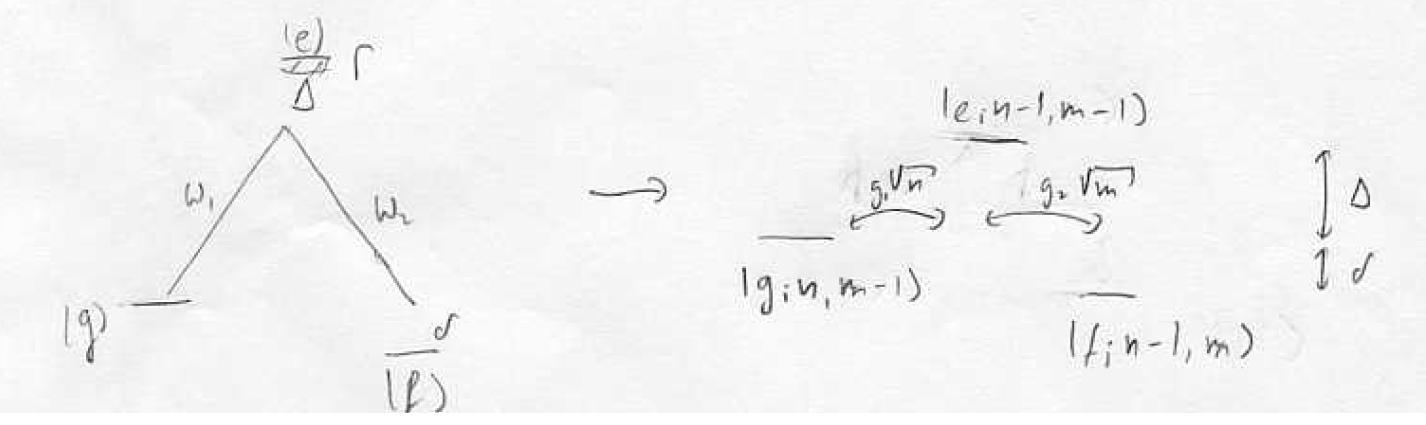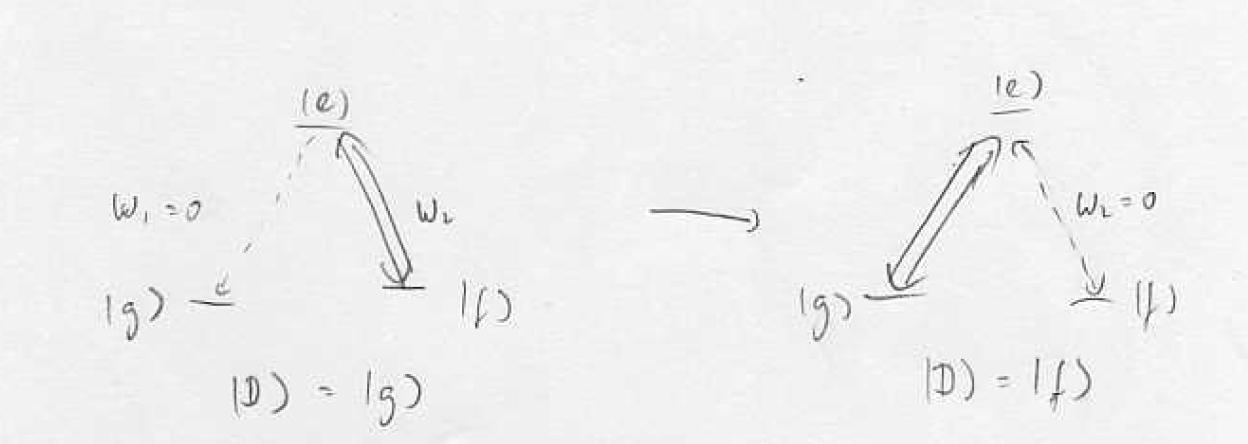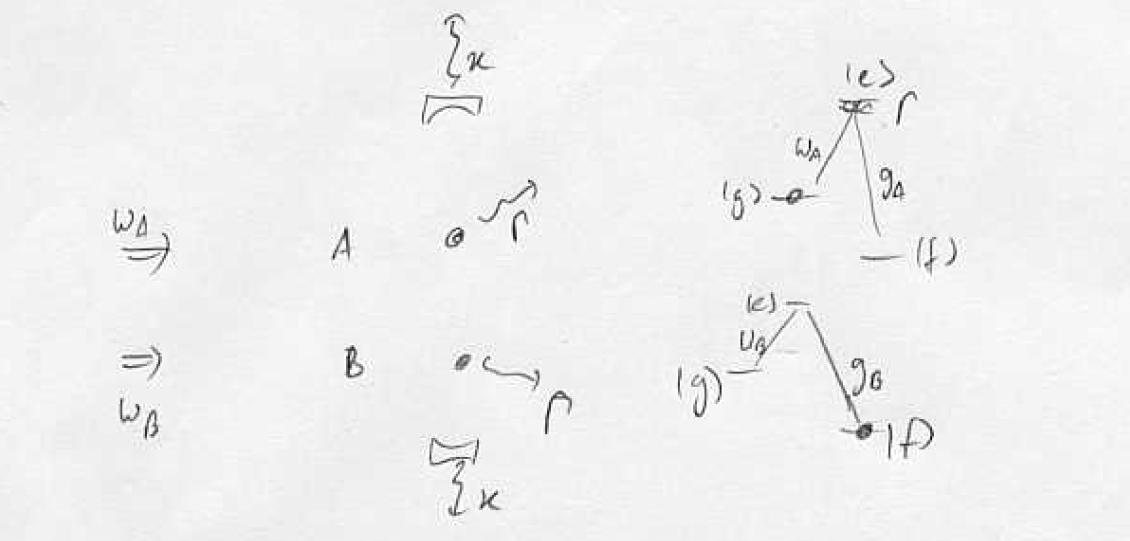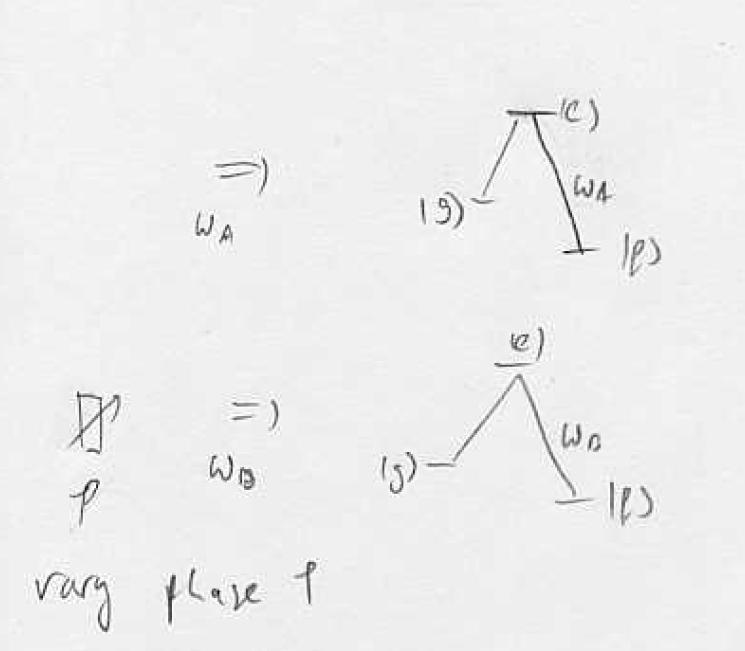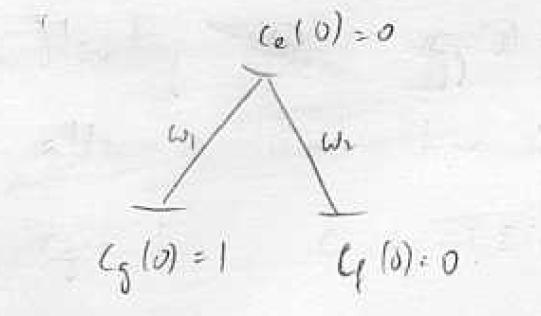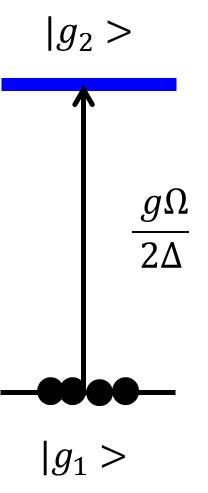Difference between revisions of "New Coherence"
imported>Gangloff |
imported>Gangloff |
||
| Line 106: | Line 106: | ||
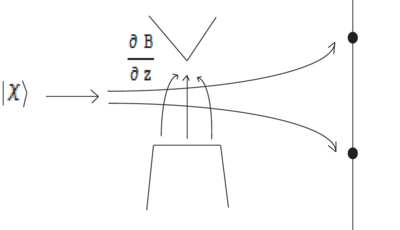
[[Image:coherence-Stern-Gerlach.png|thumb|400px|Stern-Gerlach experiment. Where, in the magnet or outside, does the projection onto <math>|\pm z\rangle</math> occur?]] | [[Image:coherence-Stern-Gerlach.png|thumb|400px|Stern-Gerlach experiment. Where, in the magnet or outside, does the projection onto <math>|\pm z\rangle</math> occur?]] | ||
| − | [[Image:coherence-stern-gerlach-wavefunctions.png|thumb | + | [[Image:coherence-stern-gerlach-wavefunctions.png|thumb|400px|Spatial wave function and corresponding spin density matrix in the Stern-Gerlach experiment.]] |
In the Stern-Gerlach experiment a particle initially spin-polarized along | In the Stern-Gerlach experiment a particle initially spin-polarized along | ||
Revision as of 00:28, 28 April 2014
We speak of coherence if there exist well defined phases between two or more amplitudes that can interfere. These can be, e.g., the relative phase of the electric field in two arms of an interferometer, the relative phase of two or more states within one atom, or the relative phase of oscillating dipole moments in different atoms. Coherence is often a measurement tool in that the relative phase is the time integral over the energy difference between the states. For instance, if the atomic states have different magnetic moments, coherence between them provides a very sensitive measurement tool for magnetic field, or if the states have different spatial wavefunctions, the relative phase is a sensitive measure of the gravitational energy difference. In atomic clocks, coherence allows one to transform as energy difference between two internal atomic states into a frequency and time standard.
Contents
- 1 Coherence in two-level systems
- 2 Three-Level System
- 3 Electromagnetically induced transparency
- 4 EIT: Eigenstates picture
- 5 STIRAP in a three-level system
- 6 Example: Five-level non-local STIRAP
- 7 On the "magic" of dark-state adiabatic transfer
- 8 Two-phase absorption, Fano profiles
- 9 Slow light, adiabatic changes of velocity of light
- 10 Superradiance
- 11 Superradiance, continued
- 12 Supperradiance in N atoms
- 13 Dicke states of extended samples
- 14 Oscillating and overdamped regimes of superradiance
- 15 Raman Superradiance
- 16 Storing light, catching photons
- 17 Notes
Coherence in two-level systems
Spontaneous Emission
Question: Spontaneous emission...
A is a unitary time evolution of the wave function of the total system
B introduces a random phase into the time evolution of the quantum system
Answer: the total system evolves by , hence is it unitary (i.e. energy conserving)
Question: The randomness of spontaneous emission occurs...
A in the measurement process of the photon
B by performing a partial trace over the states of the photon
C both A or B is possible
Answer: how do we measure a photon?
Measuring Coherence
A two-level atom can be prepared by a pulse in a superposition , where is the quantum state of the photon field after excitation. This total quantum state of the atom and photon field can be viewed as exhibiting coherence, since the initial phase between and is well defined, and the system will evolve coherently as . This occurs for times , where is the vacuum Rabi oscillation frequency, after which . After this "spontaneous emission" has occurred the state of the system is , and the quantum state of the atom has been mapped onto the photon field. The figure below displays a conceptual experiment that can be used to test this, where an interferometer is used to perform an optical homodyne detection of the light emitted by the atom and thereby obtain its phase (relative to that of the excitation light).
What about an atom prepared by a pulse in ? There is no coherence at , since the atom is in a single state, but what about ? Then the atom is in a superposition of states . Obviously some phase must exist, because otherwise no dipole moment exists that can emit, but the phase is completely unpredictable, so the experiment pictured above would yield no definite phase. Indeed the measurement would be an ensemble average over all possible phases (). We conclude that an atom prepared in does not exhibit coherence.
The ensemble average as in the figure above (parallel setups) or time average (repeated experiment at same location) yields no definite phase, so we conclude that the expectation value of the dipole moment is zero at all times (but !). What is the origin of this uncertain phase ? The answer is vacuum fluctuations.
What then happens if we place two atoms close together and excite them at the same time? Is the relative phase of the evolving dipole moments fixed or uncertain? If the relative phase is fixed, how close must the atoms be for the relative phase to be well defined? These questions about spatial coherence and Dicke superradiance will be covered later in this chapter.
Precession of a spin in a magnetic field
Precession of a spin can be viewed as an effect of coherence since . In a magnetic field (see earlier section), , corresponding to precession in the x-y plane. In other words, the precession is due to a coherence between the components of the spin. If no coherence existed, the spin would be in a statistical mixture of and , exhibiting no measurable precession. In the density matrix formalism,
in the z basis .
The expectation value of is
If the coherences (off-diagonal elements of ) were smaller, would be smaller. For a statistical mixture of and , and .
The Stern-Gerlach experiment and (ir)reversible spatial loss of coherence
In the Stern-Gerlach experiment a particle initially spin-polarized along has equal probability of following either the trajectory or the trajectory. So initially the particle is described by a density matrix for a pure state,
after passing the Stern-Gerlach apparatus (inhomogeneous magnetic field) the density matrix is
with no interference possible between the two states. Why? Because describing the full quantum state of the particle also requires accounting for its spatial wavefunction. The density matrix above does not contain all the relevant degrees of freedom. Correctly, the particle should initially be described by
with , i.e. a spatial wavefunction independent of internal state, . In the inhomogeneous magnetic field, the wavefuntion components evolve differently because there is a different potential energy seen by the two spin states :
Using the density matrix formalism:
And so the spin coherence as earlier defined is simply:
Which is indeed zero in the absence of spatial overlap of the components.
The coherence (interference) between and components to form thus exists only in the region where there is at least partial overlap between the two wavefunctions . When the wavefunctions do not overlap, there is no significance to a relative phase between and , i.e. no interference term. (Of course, if the wavefunctions are steered back to overlap, we can ask if there was a well-defined relative phase between them while they were separated.) In a more complete description, the inhomogeneous magnetic field entangles the spatial and spin degrees of freedom. When the spatial overlap disappears, or equivalently, when we trace over the spatial wavefunction (by measuring the particle either at location 1 or at location 2), the interference between and giving rise to disappears. In a measurement language, the inhomogeneous magnetic field entangles the "variable" () with the "meter" (the spatial wavefunctions of the particle). Once the spatial wavefunctions cease to overlap, the particle's position can serve as a "meter" for the variable to be measured, the spin along . However, until the particle hits the screen, or is subjected to uncontrolled or unknown magnetic fields, the meter-variable entanglement is still reversible, and a "measurement" has not been made.
Quantum Beats
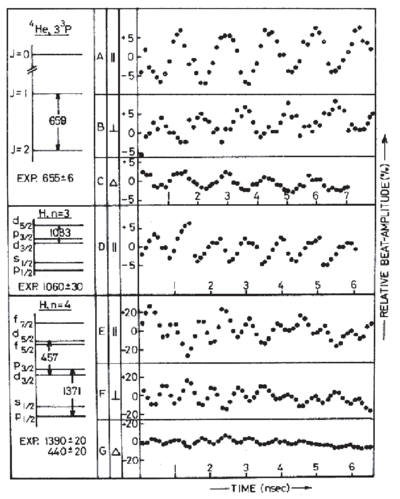
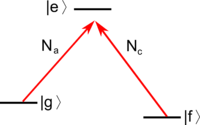
Quantum beats can be thought of as a two-level effect, though they are observed in multilevel atoms. They allow one to measure level spacings with high resolution when a narrowband excitation source (narrowband laser) is not available.
Consider the scenario of the figure on the right (Quantum Beat Levels), where we have multiple excited levels in a narrow energy interval , all decaying to a common ground state. If we excite with a pulse of duration (or a broadband source), we cannot resolve the levels, and they will be populated according to the coupling strength to the ground state for the given excitation method:
and for times , the state vector is
It follows that, in directions where the radiation from levels and interferes, there will be oscillating terms at frequencies on top of the excited state decay, i.e. the so-called "quantum beats".
This allows one to measure excited-state splittings in spite of the lack of a sufficiently narrow excitation source. Compared to our initial example of a two-level atom, here the coherence is initially purely between the excited states (definite excitation phase between them, i.e. see above ), while no coherence between and exists initially. Of course, as the atom decays, coherences between and (e.g. dipole moments) build up, and the coherence between the emitted fields of the different dipoles gives rise to the observed effect. The two following figures show respectively an idealized quantum beat signal and real data from an experimental demonstration of the technique.
Delayed Detection
Suppose we prepare a system at , but only start detection after a time , can one obtain a spectral resolution narrower than ?
Our signal is:
- ,
whose Fourier Transform is a Lorentzian
- ,
where .
Starting the measurement at is equivalent to the spectrum:
Let , then:
Of course if the absolute magnitude of the spectrum is considered, the Lorentzian part is independent of :
However at large has oscillations and a narrow central peak of order . Sub-natural linewidth spectroscopy is possible!
Note: if , and is random, then one can only measure . Thus sub-natural spectroscopy requires information on the phase of the signal at .
Clarification on coherence and dipole moment
Consider the coherence of the atom after coherent excitation with a short pulse (shorter than emission rate). Let the state of the atom be . Then, the coherence between and is maximum for , i.e. with pulse. (Coherence is in the density matrix. For a pure state, it is ). Now, let us consider a system with the atom and (external) EM mode. We consider the case where there is only a single EM mode coupled to the atom (ex, an atom strongly coupled to a cavity). Then, emission couples atomic states with photon number states: and . Thus, a pulse also maximizes the coherence and .
On the other hand, for continuous excitation (not a short pulse), saturation of the atom leads to emission of increasingly incoherent light (Mollow triplet). For Mollow triplet, see Cohen-Tannoudji p:424.
Next, consider a coherent light which is very weak. Monochromatic, coherent light is represented by a coherent state that has a Poissonian distribution of photon numbers: . For , the population of the states with is negligible, and the atom prepared in a state with emits a coherent state of light, in agreement with what is expected for small saturation.
Three-Level System
Introduction
Many interesting phenomena occur when we consider a three-level system coupled by EM radiation, such as EIT (Electromagnetically Induced Transparency, STIRAP (Stimulated Raman Adiabatic Passage), VSCPT (Velocity-Selective Coherent Population Trapping), Lasing without inversion, slowing and stopping of light, quantum memory, etc. We can consider the uncoupled levels to be internal atomic states. The interaction with coherent radiation (e.g. laser beams) "dresses" these states and the new eigenstates are coherent superpositions of the internal atomic states. On a next level of complication, we can include the mechanical effects of the radiation and consider as uncoupled states states. The radiation can then impart momentum, known as recoil momentum.
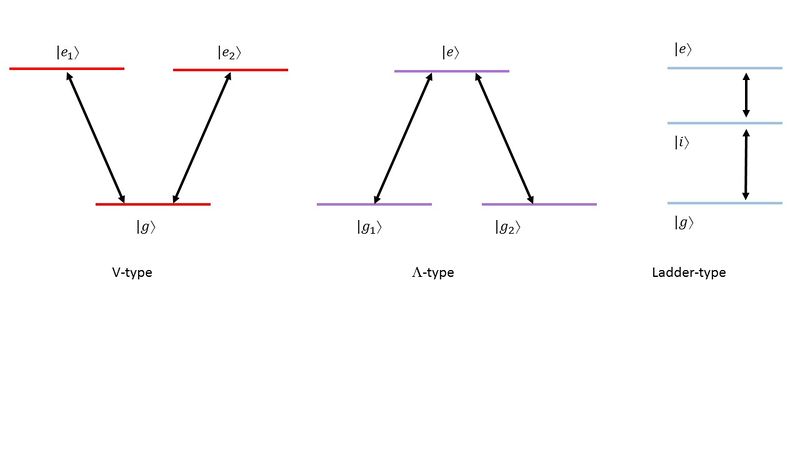
There are three basic configurations: V-type, -type, and Ladder type.
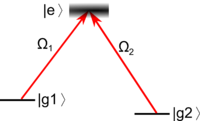
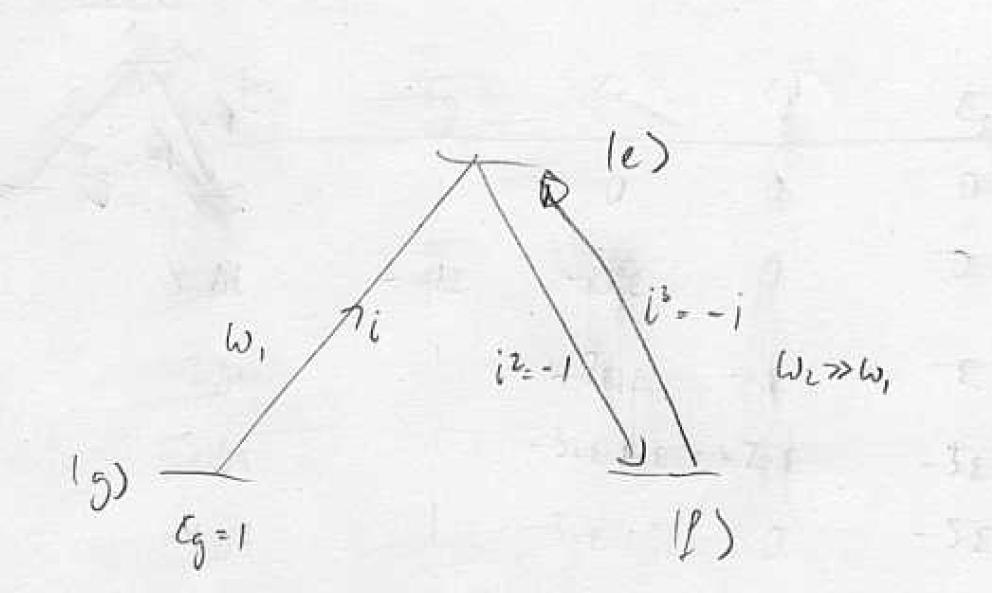
Here we focus on the -type. We can think of as two metastable states, for example, two hyperfine states in alkali atoms or the singlet and triplet lowest-energy states of alkaline earth atoms. They may or may not be degenerate. We assume that the direct transition between them is strongly suppressed, so they are only coupled to the excited state . The coupling strengths are the Rabi frequencies and (in the Electric Dipole Approximation).
Optical Pumping
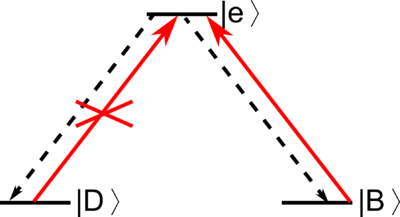
The simplest case of a 3-level system interacting with an EM field is Optical Pumping, which means that all the population is "pumped" into one state (e.g. or ). This state could be bright or dark (interacting with the light or not). For example, a dark state pumping scheme can be achieved in a system by turning on only one laser beam () which transfers all the atoms into the uncoupled state (in this case ).
Another example of Optical Pumping, which does not involve a dark state but rather a cycling transition, is pumping into a Zeeman sublevel of one of the ground state. This can be done in a multilevel system with resolved Zeeman sublevels. The state into which the population is pumped is coupled only to one excited state and that excited state can decay only to the state into which we pump: the population ends up cycling between the two.
In both of these cases, a significant fraction of the population is transferred into the excited state from which it can spontaneously decay. However, other schemes can be used in which the population is coherently transferred between different ground states with only small fraction of the population ending up in the excited state. Several such examples are discussed below.
Dark State (On Resonant Case)
Assume the semiclassical Hamiltonian with the rotating wave approximation for the system.
The second line is the interaction term. Define this as . Be careful about the notation in s. s are for energy scale. and are the energy difference of three states. and are the frequency of two lasers. s show the coupling strength and and correspond to the coupling of and and the excited state. Transforming this to the proper rotating frame, you can get rid of the exponential factors.
When the lasers are on resonant to the energy level difference, the Hamiltonian in the matrix form is as follows.
Diagonalizing this, you get the energy eigenvalues , and and corresponding eigenstates , and The first eigenstate is not mixed with the excited state, and therefore the photon cannot talk to this state. This state is called dark state.
This can be also proved by calculating
For , the dark state is . Dark state is predominantly the state with weaker coupling. The orthogonal superposition of two stable states is the bright state.
Coherent Population Trapping
When you have a three level system two of which are stable or metastable, you can make a coherent superposition of the two stable states by shining lasers. This phenomenon is called coherent population trapping.
The system is analyzed in the previous subsection. You have the dark state that does not talk with the photon and the bright state that talks with the photon. When you keep shining the photon, population in the bright state is excited to the excited state and the excited state can decay to both the dark state and the bright state. However, the dark state cannot be excited again. Therefore, population moves to the dark state in the same way as the optical pumping. Difference between the optical pumping is that the dark state is now the superposition of the two state. By adjusting the ratio of and , you can make the arbitrary superposition of two stable states.
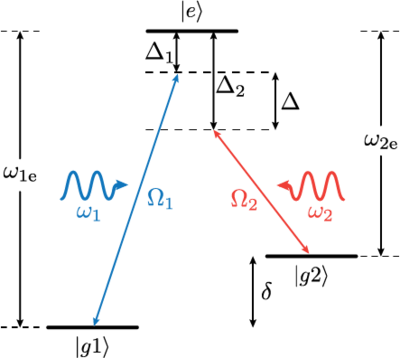
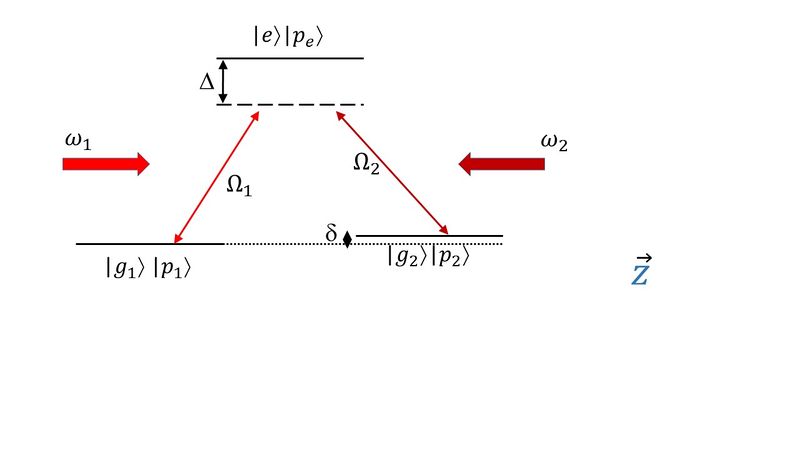
Effective 2-level System: Dark State (Off Resonant Case)
(Here we follow D. A. Steck, Quantum and Atom Optics, Chapter 6.)
Consider a configuration and let's ignore the external degrees of freedom for now. If , we can treat the 3-level system as an effective two level system. here is the detuning from the excited state (for each of the two lasers). One way to think about this is that each coupling beam creates a coherence between and respectively. This is similar to two dipoles oscillating in phase. The result is that population can be transferred coherently from one ground state to the other, without resorting to spontaneous emission from the excited states to transfer the atoms which could destroy this coherence. Another way to think about this process is that the two Raman beams can interfere, creating two beat frequencies, one of which can be tuned to the energy difference between the two ground states.
To mathematically describe the effective two-level system, we have to adiabatically eliminate the excited state from the discussion. To do this, we can first transform into a frame rotating at the laser frequencies. We pick the excited state as the energy reference and our state becomes:
Here and are the slowly-varying amplitudes. We pick the zero of the energy to be at and, for simplicity, assume . We also assume the two laser frequencies are on 2-photon resonance. Then, in the RWA and in the rotating frame we just defined, and in the basis , the Hamiltonian is:
From here, we can write the Schrodinger equation for the three amplitudes:
We can now assume that the excited state amplitude evolves at a frequency determined by the detuning . But since we want to be large compared to the timescale of the dynamics of the system (which is set by ), we can neglect its time variation: . We can then solve the system of equations above by eliminating to get (now in the basis )
We recognize the off-diagonal entries as the two-photon Rabi frequency. The eigenenergies and eigenstates are:
The dark state is the coherent superposition of uncoupled states which does not interact with the light.
External states: VSCPT
If we now include the mechanical action of the laser beams, the atoms will acquire momentum when they absorb or emit photons. We now describe our system with the uncoupled states , as in the figure. Consider an atom having momentum in the direction. Then, from momentum and energy conservation, we get the Raman resonance condition:
We can see that this condition is satisfied only for one velocity, , which means that if we have an ensemble of atoms with different velocities, we can target the ones with velocities . The width depends on the Rabi frequencies.
We can perform a similar analysis as the one above and we find that there is a dark state in this system too. In the simple case when (degenerate ground states) and , the dark state is:
we can see that now internal and external states are entangled.
The sensitivity of Raman transitions to velocities together with the existence of a dark state, can be used to prepare a sample of very cold atoms atoms: atoms with velocities close to 0 (for example) can be targeted and transferred to the dark state. For example, VSCPT is a method based on these observations which results in a cold sub-recoil ensemble.
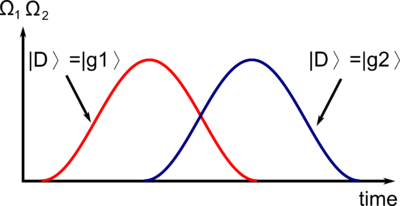
STIRAP
What happens if you change and slowly, i.e. adiabatically? Stimulated Raman adiabatic passage, STIRAP, is an application for this situation.
For simplicity, let's assume that and lasers are blue detuned. You first turn up the laser 2 and then turn up the laser 1, turning down the laser 2. In the end, you turn down the laser 1. In this condition, the dark state is initially , as . Then the dark state gradually becomes . Thus, you can coherently move the population from to . Here, the dark state is the lowest energy state, because it has no AC Stark shift, whereas the energy level of the bright state goes up due to the blue detuned light. The pulse sequence is counter-intuitive. In order to talk to the atoms in , you first turn up the laser that connects and .
When you have the red detuned light and when and are not degenerate, you get the same result. In these cases, and are generate, where and are the photon number for the laser 1 and 2.
STIRAP is a dark state transfer. How can we go from to without building up population in ? The answer is, there is a slight population in . Let's check this with Schr\"{o}dinger equation.
As we want after the time for the transfer,
The probability for the spontaneous emission is
as or . However, has to be smaller than coherent time of the and states.
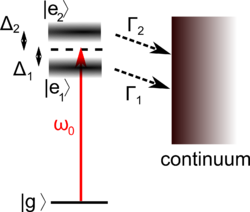
Gain without Inversion
When you have a laser, common belief is that you need to have more atoms in excited state than ground state. However, this is not necessarily the same for the three level system B system with two unstable states that decay by coupling to the same continuum (i.e. same polarization). Suppose you send the population from the ground state by shining a laser of a frequency between two excited state energy. The matrix element for the transition by the second order perturbation theory is
There is an for which the two terms almost cancel, when . When you have atoms in ground state and send the laser of frequency , you will see a quantum interference due to the multiple path to the continuum. When you have a population in state that is much smaller than that in the ground state and you shine the laser, you see the light due to the laser itself plus the induced emission of from . There is a gain in this frequency though there is no population inversion. In other words, there is destructive interference between and for the absorption from the ground state, but not for the gain.
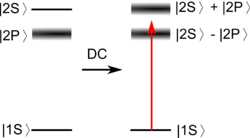
There are some possible realization for this system. One is hydrogen and DC electric field. The mixing of 2S state and 2P state by the DC electric field gives two wide field. Another is to use AC electric field to mix the S state and P state. If you have system with two degenerate ground state, you can make a gain without inversion by distributing the population as follows: none in , a little in and most in , whose population is hidden.
For more detailed discussion, refer to Phys. Rev. Lett. 62, 1033.
http://prl.aps.org/abstract/PRL/v62/i9/p1033\_1
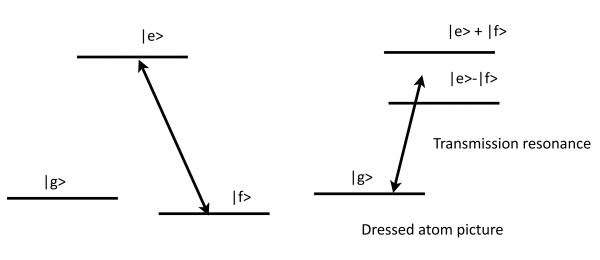
Electromagnetically induced transparency
EIT in the dressed state picture
"Is it possible to send a laser beam through a brick wall?"
Radio Yerevan: "In principle yes, but you need another very powerful laser..."
The light interaction Hamiltonian in the dipole approximation is , where the dipole operator is comprised of individual dipole moments and corresponding to the transitions and , respectively. In expanding out the interaction Hamiltonian we drop the cross terms , thus assuming that does not couple and visa versa (this assumption is justified if the ground state splitting is much larger than the detuning of the light fields). The interaction Hamiltonian then becomes
where we have introduced the Rabi frequencies, .
As usual in semi-classical light matter interaction problems, we switch to the rotating frame of the light field defined by
- .
The total Hamiltonian in this new basis is thus
Steve Harris thought initially of special, ionizing excited states. However it is possible to realize the requirement of identical decay paths in a -system with a a(strong) coupling laser. The phenomenon is closely related to coherent population trapping.
For resonant fields , we have
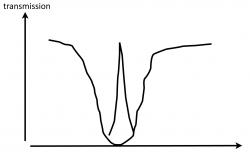
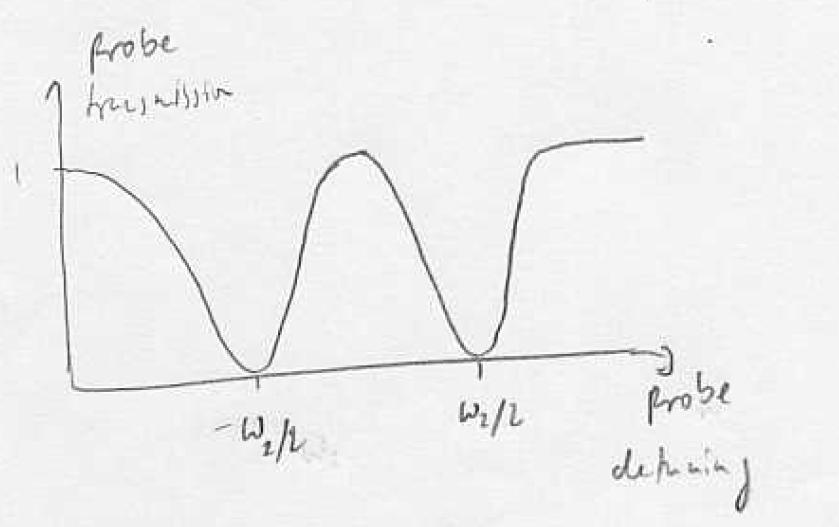
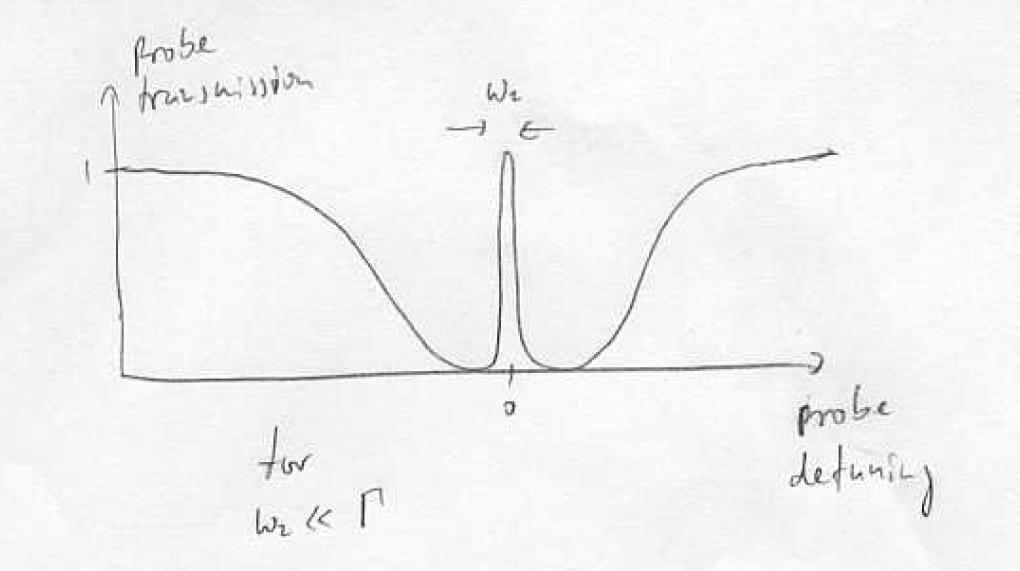
As we turn up the power of the coupling laser the transmission improves and then broadens (in the realistic case of a finite decoherence rate , an infinitesimally small coupling Rabi frequency, but the frequency window over which transmission occurs is very narrow and given by .
EIT vs CPT. What's the difference?
Sometimes in the literature CPT and EIT are treated as two different phenomena, while here we have treated the two with a similar formulation. Are they different? The short answer is no. The long answer is that CPT is a "trapping" effect, and relies on spontaneous emission to produce the coherent dark state (i.e., spontaneous emission allows for the system to undergo a random walk in phase space until it falls into a "trapped" state, no longer coupled to spontaneous emission). For example, in VSCPT, very low temperatures are attained because the the atoms undergo many spontaneous emission events and are pumped into the dark state. On the other hand EIT experiments are usually prepared adiabatically: A strong pump beam initializes the atomic state, and then the weak probe beam adiabatically prepares the dark state, with no spontaneous emission. Another contrast is that CPT experiments focus on trapping of atoms, while EIT experiments are more concerned with the effect of the atoms on cross-modulating the two light beams. However, the underlying physics for both effects is the same.
Further theoretical treatment
The approach to EIT presented here has relied greatly on intuition. For the interested reader, there are two very interesting approaches not covered here. The first is using the optical Bloch equations (which are outside the scope of 8.421) to treat the effect of spontaneous emission explicitly, and thus calculate the widths of the EIT resonance feature. A good resource for this is the section "Master equation and linear susceptibility" in Rev. Mod. Phys. 77, 633 (2005). http://journals.aps.org/rmp/abstract/10.1103/RevModPhys.77.633
Another approach is to ask the question: Is EIT a quantum effect? In many ways it is not, and it can be modeled by a coupled system of two mass-spring harmonic oscillators, which is studied in careful detail here: http://arxiv.org/abs/quant-ph/0107061 .
EIT: Eigenstates picture
Using the field quantization to easily include energy conservation, we see that the states are coupled in triplets:
So the Hamiltonian is given by
On resonance the Eigenstates are
In the limit of weak probe and a strong pump,
we can limit the analysis to . Then we can diagonalize the strong coupling, and treat the probe perturbatively
Again we have a scattering problem
via a two photon process. The matrix element contains two intermediate states with opposite detunings.
On one- and two-photon resonance all couplings are symmetric in and , the detunings are opposite, and the matrix element M vanishes: electromagnetically induced transparency (EIT). If the pump remains on resonance and we tune the probe field, then the couplings are still symmetric in , , but the detunings are , and the matrix element does not vanish. Maximum scattering is obtained when we tune to one of the bright states
When we include the decay within the system, we can no longer use the Hamiltonian formalism, but must use density matrices. Nevertheless, the eigenstates provide physical insight into the problem.
STIRAP in a three-level system
If at least one of the two coupling beams is non-zero, there is always a finite energy spacing between the dark state and the bright states. This allows one, by changing the ration of the coupling beams, to adiabatically change the character of the dark state between |g> and |f> while not populating the bright states (and thus the excited state). By use of the so-called "counterintuitive pulse sequence"
STIRAP of this type in a three-level system is also called "dark-state transfer."
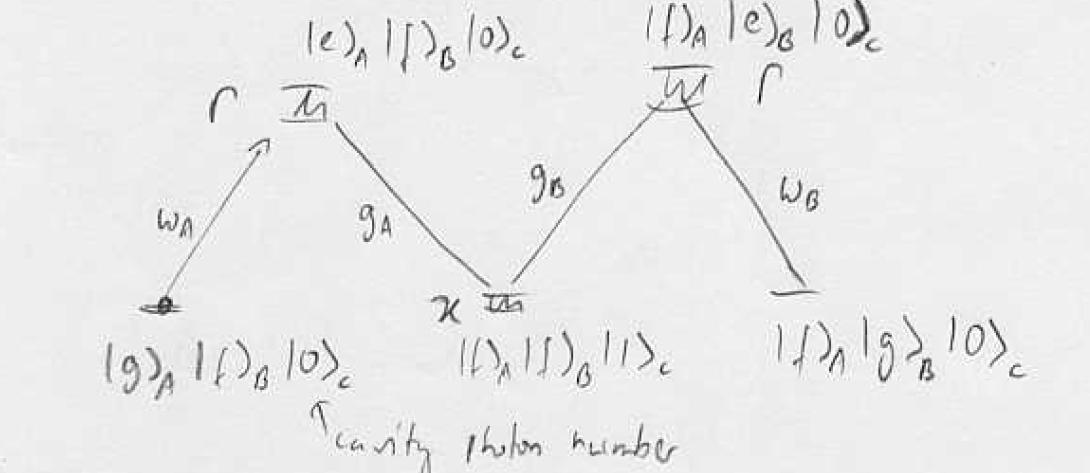
Example: Five-level non-local STIRAP
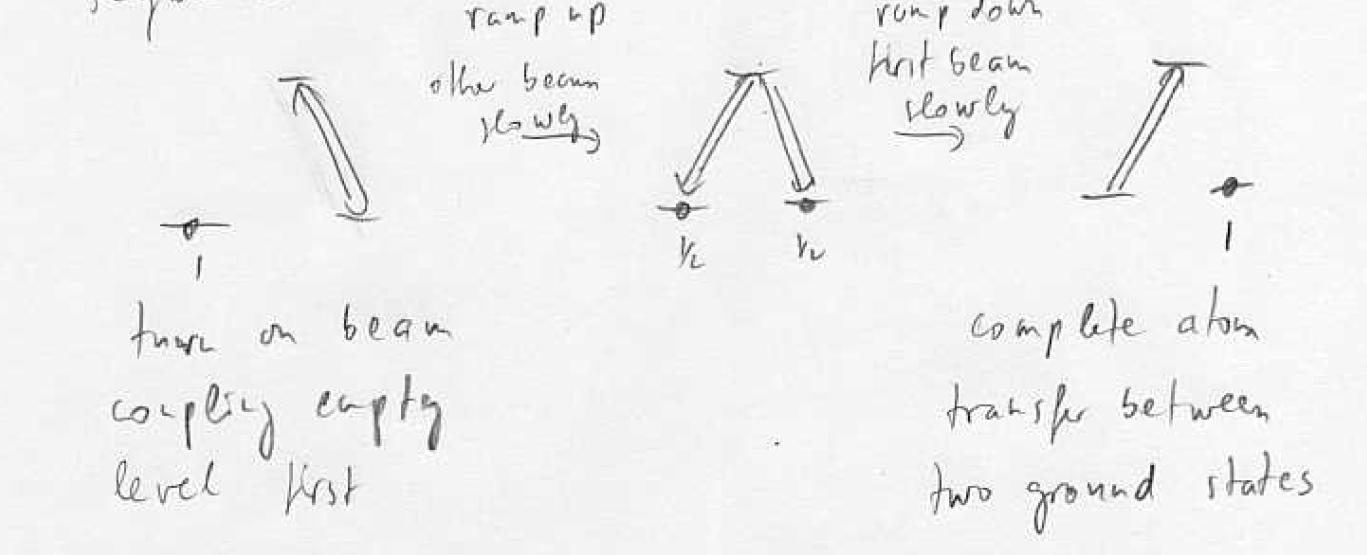
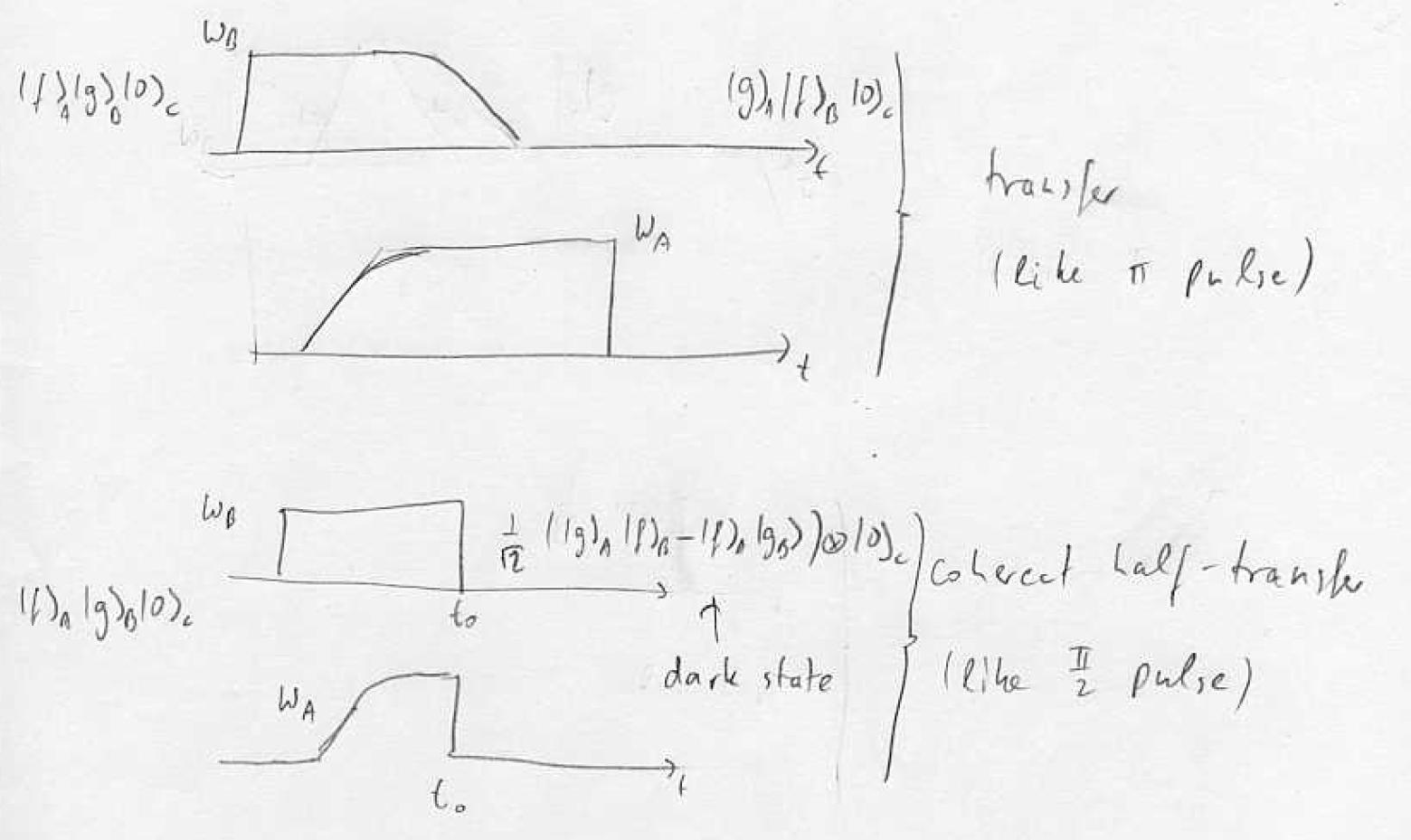
Atom A contains hyperfine excitation, can we transfer the hyperfine excitation from A to B without losing it from the cavity? Cavity strongly coupled to A,B with single-photon Rabi frequency g. Dark-state adiabatic transfer with virtual excitation of the cavity mode is possible:
Procedure: turn on first coupling empty level, ramp up , ramp down adiabatic transfer via dark state of the cavity. Note that the probability to find the photon in the cavity can be made very small while maintaining full transfer: virtual states.
If we stop the transfer suddenly half-way we create an entangled state where the single hyperfine excitation is shared between the two samples.
Verification and entanglement:
well-defined phase must exist
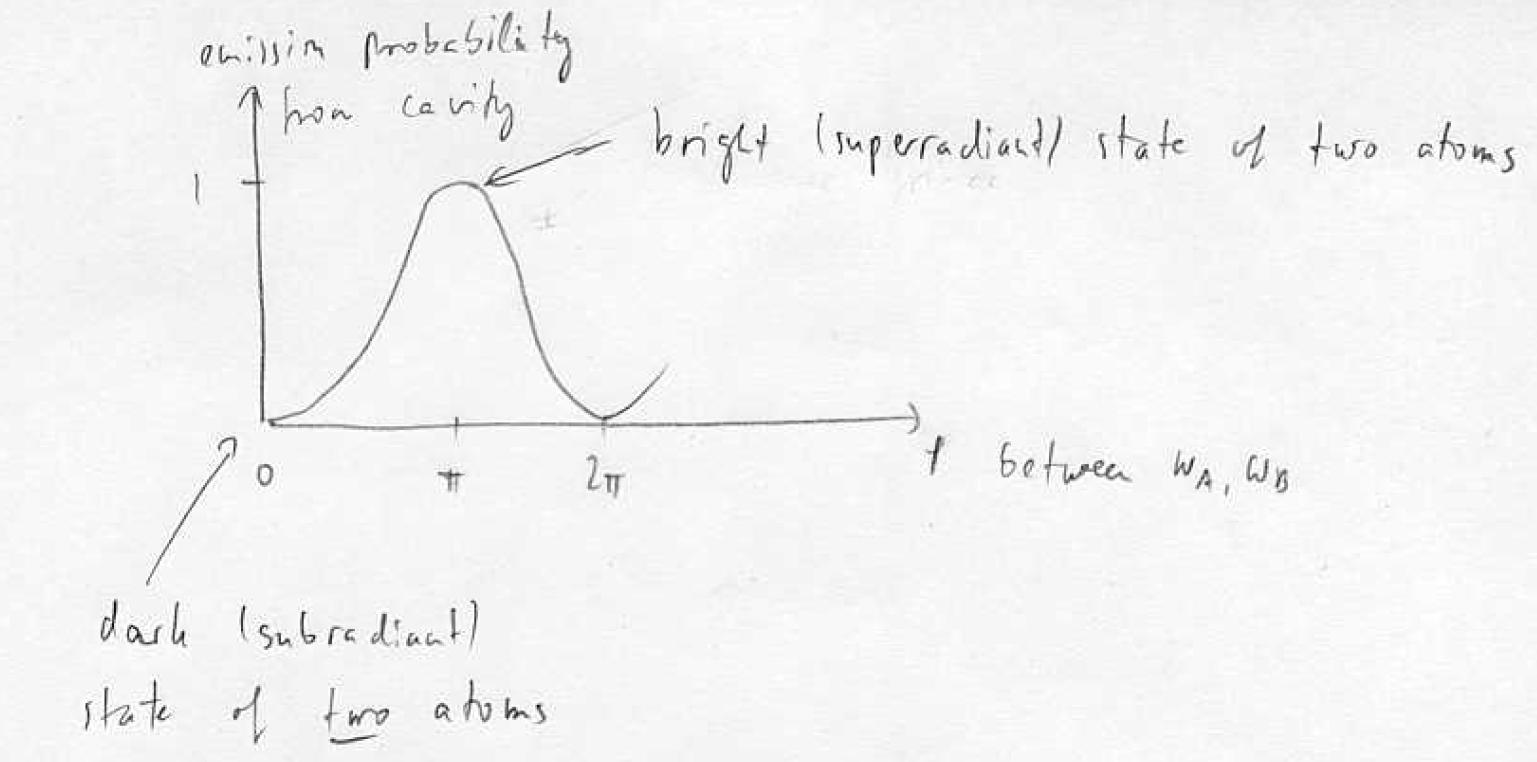
How to verify? Simultaneous readout, super and sub radiant states
The dipole moments (emitted fields on the ge transition) of the two atoms can interfere.
Interference fringe can only be observed if state is entangled. Fringe is due to interference if dipole moments between <underline> <attributes> </attributes> different </underline> atoms.
On the "magic" of dark-state adiabatic transfer
How is it that we can transfer the population completely form state |g> to state |f> through the state |e> while keeping the unstable state |e> unpopulated? (The correct statement is "...while keeping the population of |e> negligibly small"). This is possible through coherence-interference: n resonance the eqs of motion for the amplitude read
For adiabatic transfer we have and amplitude flow as
So we see how |f> accumulates amplitude because it arrives there always with the same phase factor -1, whereas the flow back from |f> into |e> leads to a destructive interference in |e> with the amplitude flow from |g>, keeping the amplitude in |e> small at all times, while the amplitude on |f> keeps growing. If the state |f> were to acquire a random phase <underline> <attributes> </attributes> relative to |g> </underline> due to some other interaction, then the constructive interference leading to the accumulation of amplitude in |f> and the destructive interference in |e> would not work. The dark state transfer requires g-f coherence.
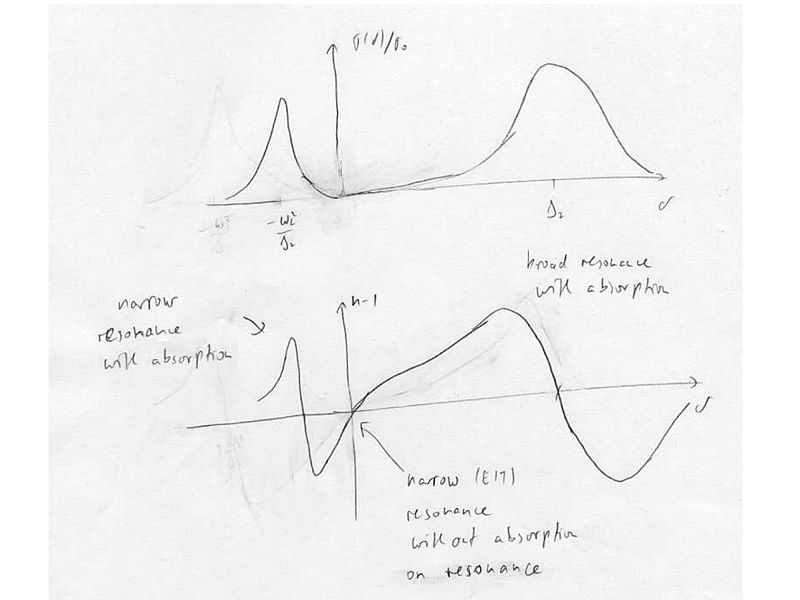
Two-phase absorption, Fano profiles
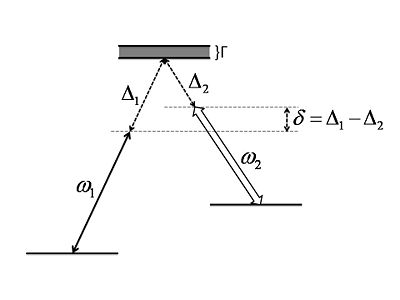
Let us assume large one-photon detuning, , weak probe and strong control field (we also define the two-photon detuning ).
In this limit analytic expressions for the absorption cross section for beam and the refractive index seen by beam exist, e.g. [Muller et al., PRA 56, 2385 (1997)]
The refractive index is given by:
where is the atomic density, .
For zero ground-state linewidth (decoherence between the ground-states) where is the resonant cross-section, and .
The absorption cross section for :
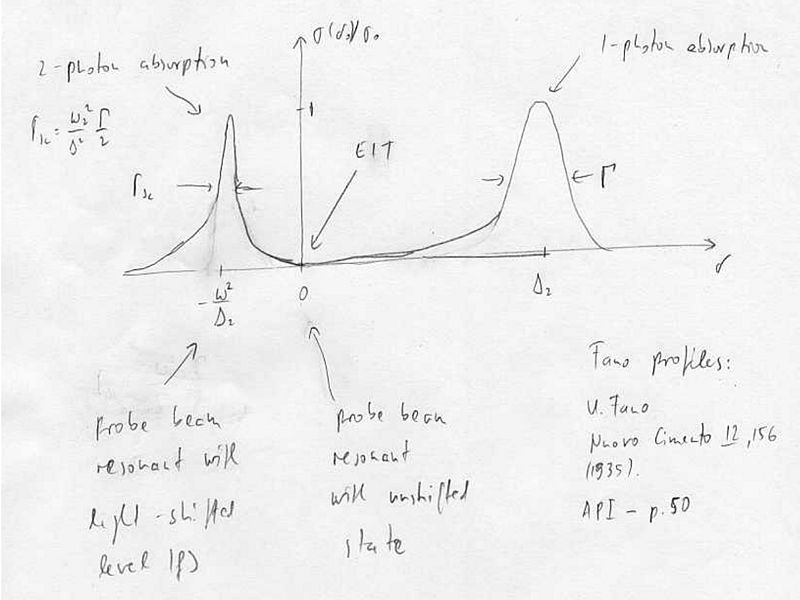
This is like a ground state coupling to one narrow and one wide excited state, except that there is EIT in between because both states decay to the same continuum.
At , we have one-photon absorption, which is a two-photon scattering process:
At , two-photon absorption, which is (at least) four-photon scattering process:
For the EIT condition , there is no coupling to the excited state, and the refractive index is zero. In the vicinity of EIT, there is steep dispersion, resulting in a strong alteration of the group velocity of light slowing and stopping light.
Slow light, adiabatic changes of velocity of light
The group velocity of light in the presence of linear dispersion is given by [Harris and Hau, PRL 82, 4611 (1999)]
for light at frequency .
A strong linear dispersion with positive slope near EIT then corresponds to very slow light.
As , the electric field is unchanged so the power per area also remains unchanged.
Due to slowed group velocity, the pulse is compressed in the medium. As a consequence, the energy density is increased, and the light is partly in the form of an atomic excitation (coherent superposition of the ground states, although most of the energy is exchanged to the control field).
For sufficiently small , the velocity of light may be very small, down to a few m/s [L.V. Hau, S.E. Harris et al., Nature 397, 594 (1999)], as observed in a BEC. Reduced group velocity can also be observed in room-temperature experiment if the setup is Doppler free (co-propagating probe and control fields and ) (otherwise only a small velocity class satisfies the two-photon resonance condition).
If we change control field adiabatically while the pulse is inside the medium, we can coherently stop light, i.e. convert it into an atomic excitation or spin wave. With the reverse process we can then convert the stored spin-wave back into the original light field. The adiabatic conversion is made possible by the finite splitting between bright and dark states. In principle, all coherence properties and other (qm) features of the light are maintained, and it is possible to store non-classical states of light by mapping photon properties one-to-one onto quantized spin waves. We will learn more about these quanta called "dark-state polaritons" once we have introduced Dicke states. Is it possible to make use of EIT for, e.g. atom detection without absorption? Answer: no improvement for such linear processes. However: improvement for non-linear processes is possible.
Superradiance
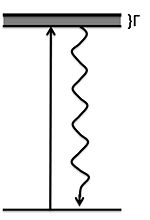
Let's assume there are two identical atoms, one in its ground and the other in its excited state. They are placed within a distance of each other. What happens?
For a single atom, the emission rate at time t is (product of the spontaneous emission rate and occupation probability). Thus, the emission probability to have emitted a photon by time t is
(eqtn:superradiance1)
What happens to the two atoms case if there is only one atom in the excited state? It turns out that the correct answer is
(eqtn:superradiance2)
(eqtn:superradiance3)
The photon is emitted with the same initial rate, but has only probability of being emitted. It is saying there is still half probability for the atom remaining in the excited state. How can we understand this? The interaction Hamiltonian is:
(eqtn:superradiance5)
In QED:
(eqtn:superradiance6)
with
Lecture XXVI
Superradiance, continued
Now we can write the initial state as:
where
and
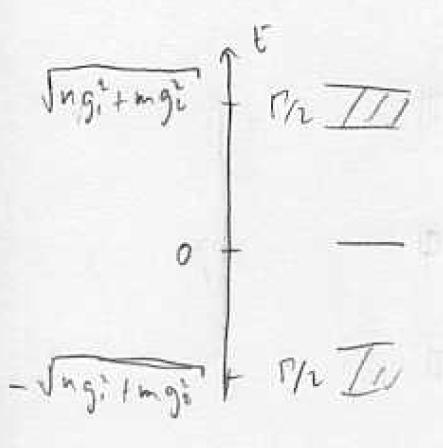
The initial state has a 50% probability to be the sub-radiant state, hence the system has a 50% probability of not decaying. The set of four states can be organized into a triplet and a singlet:
The state is "dark" in that it does not decay under the action of the Hamiltonian V. The matrix elements between the states, indicated by arrows, are expressed in units of the single atom coupling .
Just as we can identify the two-level system , with a (pseudo)spin , we can identify the triplet and singlet states with , and write
Since V conserves parity (exchange of the two atoms), there is no coupling between singlet and triplet states. (This is no longer true when we consider spatially extended samples).
Supperradiance in N atoms
First look at N spins in a magnetic field (NMR)
Dipole moment: , power radiation . There is N times more enhancement over N.
For N excited atoms, we usually regard the atoms as independent. Therefore, power radiation scales as N.
BUT: All two-level systems are equivalent. Which picture is correct?
Answer: There is an important distinction between sample size and sample size . For sample size , which is usually the case for optical transitions, the particles can be treated independently. For sample size , all particles interact with a common radiation field and thus cannot be treated independently.
The coherence in spontaneous emission for N (localized) atoms requires two assumptions:
1. No interaction between atoms 2. Emitted photons (NOT the atoms) are indistinguishable. The particle symmetry (Bosons, Fermions) is irrelevant.
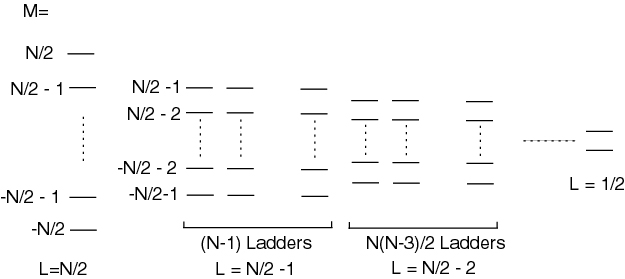
The Dicke states, equivalent to the states obtained by summing N spin particles, are
Interaction with em field through ,
Matrix element responsible for spontaneous emission:
Note matrix element only couple within one ladder. For single particle, . Rate (or intensity I) of radiation relative to a single particle:
Let's look at
1. 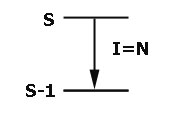 Radiation rate I is the same as for N independent atoms
Radiation rate I is the same as for N independent atoms
2. 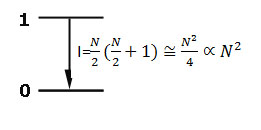 Radiation rate I , N times enhancement compared with N independent atoms characteristic for superradiant systems
Radiation rate I , N times enhancement compared with N independent atoms characteristic for superradiant systems
3.  . Only one particle is excited. BUT: I=N N times enhancement.
. Only one particle is excited. BUT: I=N N times enhancement.
The matrix element can be calculated as . We can also get the matrix element by symmetry argument (should be the same as ).
Let us look at the leftmost (symmetric) ladder. Near the middle of the Dicke-ladder, , the matrix element is The emission rate is proportional to , i.e. the rate is quadratic in atom number.
Classically, that is not too surprising: we have N dipoles oscillating in phase, which corresponds to a dipole , the emission is proportional to . However, the Dicke states have and nevertheless macroscopic emission. How do we see this? In the Bloch sphere, for the angular momentum representation the coherent state corresponds to all atoms in the ground state.
A field that symmetrically couples to all atoms (e.g. pulse) acts only within the completely symmetric Hilbert space . This space consists of states like , corresponding to rotations of the state around some axis on the Bloch sphere.
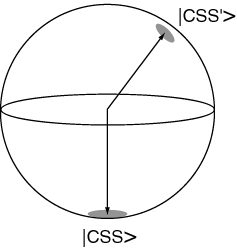
The states obtained by rotations of the state by symmetric operations that act on all individual atoms independently, i.e. of the form , are called coherent spin states (CSS). They are represented by a vector on the Bloch sphere with uncertainties in directions perpendicular to the Bloch vector.
If we prepare a system in the CSS corresponding to a slight angle away form near , then classically it will obey the eqs of motion of an inverted pendulum, and fall down along the Bloch sphere. (This can be shown using the classical analogy with a field.)
Question1: So what happens if we prepare the state ? Does it:
a. evolve down along the Dicke ladder maintaining (but )?
b. fall like a Bloch vector along some angle chosen by vacuum fluctuations?
Answer: there is no way of telling unless you prepare a specific experiment. If we detect (with unity quantum efficiency) the emitted photons, then each detection projects the system one step down along the Dicke ladder, and .
If we measure the phase of the emitted light, say with some heterodyne technique, then we find that the system evolves as a Bloch state.
Question2: Is there enhanced induced emission or absorption?
Answer:No. initial state , single particle , N particles . Consequently, it takes exactly half a Rabi period to completely invert the population as for a single atom. There are N Dicke steps with N times larger matrix elements. In contrast, for spontaneous emission, there are N Dicke steps, with times larger matrix elements N times faster.
Dicke states of extended samples
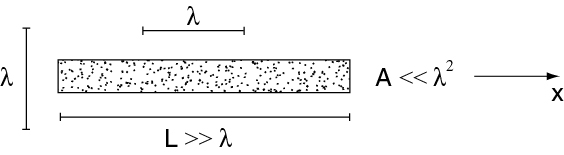
Consider an elongated atomic sample
such that a preferential mode (along x) is defined. Emission into solid angle can be coherent. Thus, the total radiation intensity is enhanced by a factor of about . This is analogous to optical amplification gain cross section . Formally, we can define Dicke states with respect to the preferred mode as
etc.
Then one can easily see that the phase factors are such that the interaction Hamiltonian
is such that the Dicke ladder has the same couplings as before, i.e. superradiance occurs. However, emission along a direction other than the preferred mode now leads to diagonal couplings between the Dicke ladders , since emission along some other direction with operator does not preserve the symmetry of the state with respect to permutations of the atoms. However, if the atom number along the preferred direction is large enough, superradiance still occurs. The condition for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\ll\lambda^2} is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\geq 2} , but for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A>\lambda^2} the condition is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{N\lambda ^2}{A}>1} . This is exactly the condition for sufficient optical gain in an inverted system for optical amplification (lasing) to occur, since is the stimulated emission cross section for an atom in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |e>} .
Observation in a BEC, in multimode optical cavities.
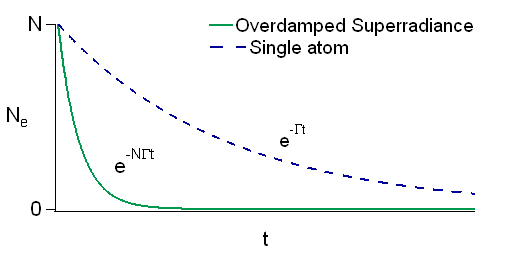
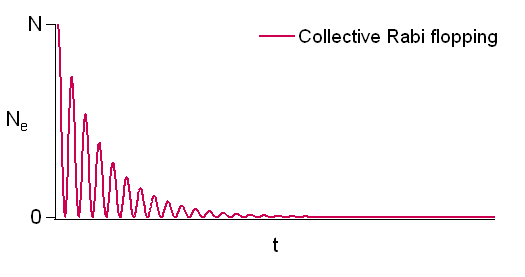
Oscillating and overdamped regimes of superradiance
The photon leaves the sample in a time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{L}{c}} . If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{N}g<\frac{c}{L}} , then the damping is faster than Rabi flopping, and we are in the rate equation limit where the emission proceeds as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{(\sqrt {N}g)^2}{c/L}=\frac{Ng^2L}{c}} , rather than as emission by independent atoms that would decay as . If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt {N}g>\frac{c}{L}} , then Rabi flopping occurs during the decay.
Note:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = g^2L/C} .
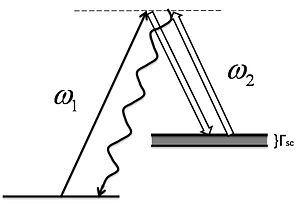
Raman Superradiance
In the limit of large detuning and low saturation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega \ll \Delta } , we can eliminate the excited state by using the dressed atoms' picture. The dressing beam Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} is making a two-photon resonance from to . From another picture, it is also mixing the two levels and . If we eliminate the excited state, we will get a effective two level system.
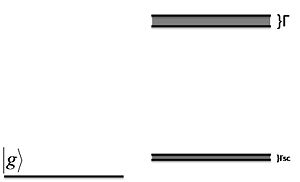
For the mixing level , the scattering rate will be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{sc}=\frac{\Omega^2}{\Delta ^2}\frac{\Gamma}{2}} .
Now we find We can adjust the linewidth Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{sc}} via Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} for the effective excited state .
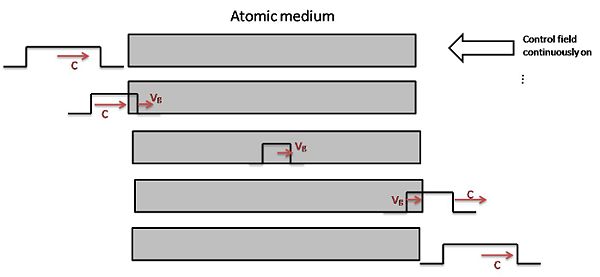
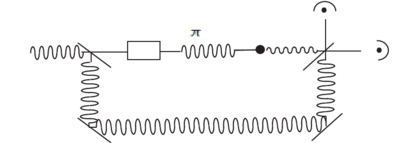
Storing light, catching photons
When we consider a quantized field on the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |g_1>\rightarrow |e>} transition and a classical control beam connecting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |g_2>} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |e>} , there is a family of dark states for the collective three-levels systems, corresponding to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=0,1,2,...} excitations in different spin manifolds for a N photons input state.
(Lukin, Yelin, and Fleischhauer PRL 84, 4232 (2000)).
When Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega \gg Ng^2} , these states are purely photonic. When Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \ll Ng^2} , these states are purely atomic excitations.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega \gg Ng^2 :|D,n> \rightarrow |n>_{\mathrm{photons}}|L,M=-L>_{\mathrm{atoms}} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega \ll Ng^2 : |0>_{\mathrm{photons}}|L,M=-L+n>_{\mathrm{atoms}}}
In general, these excitations n=0,1,2,... are called dark state polaritons. They are a mixture of photonic excitations and spin-wave excitations.
By adiabatically changing after the pulse has entered the medium, we can map any photonic state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi >_{\mathrm{photon}}=\Sigma c_i|i>_{\mathrm{photon}}} onto a spin wave, store it and map it back onto a light-field by turning on the coupling laser Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega } again.






























![{\displaystyle \langle {\hat {\sigma }}_{x}\rangle =Tr[\rho {\hat {\sigma }}_{x}]=Tr\left({\begin{array}{cc}{\frac {1}{2}}e^{-i\omega _{L}t}&{\frac {1}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}e^{i\omega _{L}t}\end{array}}\right)=\cos \omega _{L}t.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9d0aea923dce7dc4a7623215831fbc0af38ef5)