Tmp Lecture 25

<framebox> <attributes> <width>None</width> <pos>None</pos> </attributes> Lecture XXV </framebox>

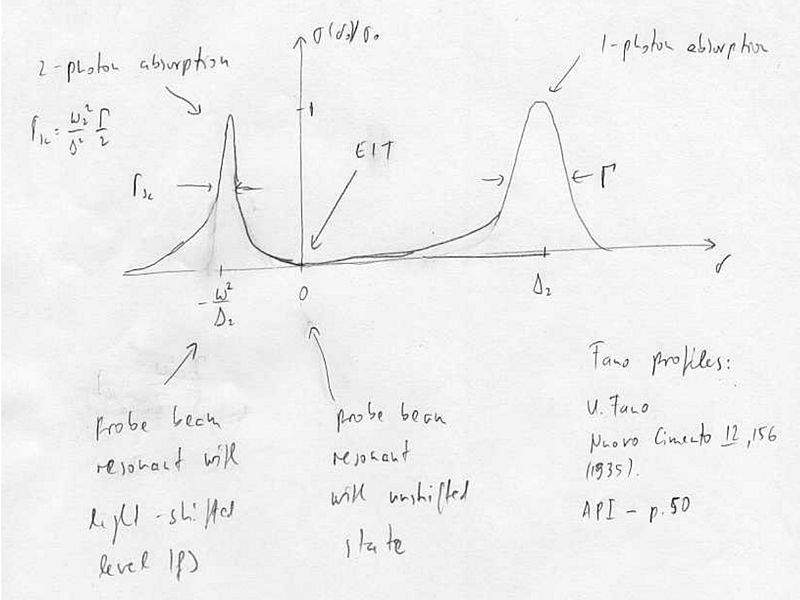
Two-phase absorption, Fano profiles

Let us assume large one-photon detuning, $\Delta \gg \Gamma$, weak probe $\omega _{1}$ and strong control field $\omega _{2}$ (we also define the two-photon detuning $\delta =\Delta _{1}-\Delta _{2}$).

Image

In this limit analytic expressions for the absorption cross section for beam $\omega _{1}$ and the refractive index seen by beam $\omega _{1}$ exist, e.g. [Muller et al., PRA 56, 2385 (1997)]

The refractive index is given by: $n(d)=1+{\frac {3}{8\pi }}{\tilde {n}}\lambda ^{3}f(\Delta )$

where ${\tilde {n}}$ is the atomic density, $f(\delta )={\frac {\Gamma }{2}}\delta {\frac {A}{A^{2}+B^{2}}},A=\omega _{2}^{2}-\delta \Delta _{2},B=\delta \Gamma$.

For zero ground-state linewidth (decoherence between the ground-states) $\sigma (\delta )=\sigma _{0}.g\left(\delta \right)$ where $\sigma _{0}={\frac {3}{2\pi }}\lambda ^{2}$ is the resonant cross-section, and $g(\Delta )={\frac {\Gamma }{2}}{\frac {\delta B}{A^{2}+B^{2}}}$.

The absorption cross section is for $\Delta _{2}>0$

This is like a ground state coupling to one narrow and one wide excited state, except that there is EIT in between because both states decay to the same continuum.

Image

At $\delta =\Delta _{2}$ , we have one-photon absorption, which is a two-photon scattering process:

Image

At $\delta =-{\frac {\omega _{2}^{2}}{\Delta _{2}}}$, two-photon absorption, which is (at least) four-photon scattering process:

Image

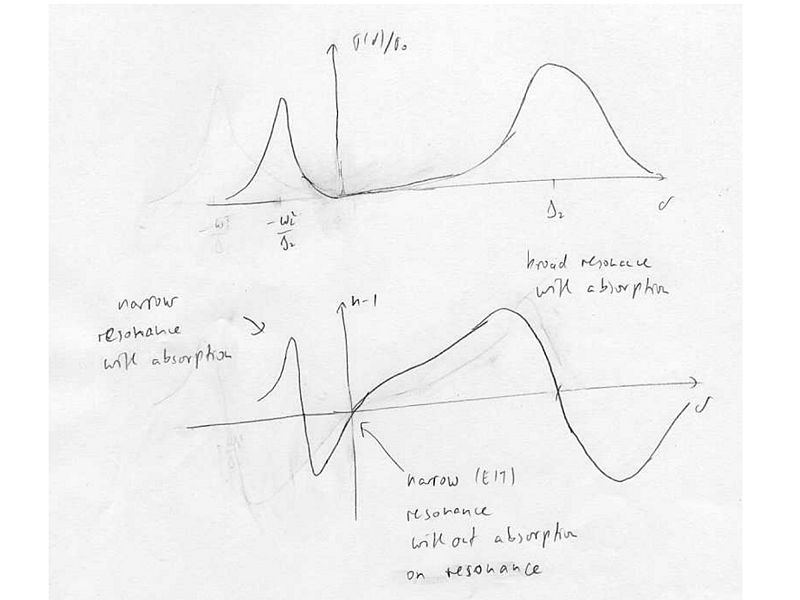
For the EIT condition $\delta =0$, there is no coupling to the excited state, and the refractive index is zero. In the vicinity of EIT, there is steep dispersion, resulting in a strong alteration of the group velocity of light$\rightarrow$ slowing and stopping light.

Slow light, adiabatic changes of velocity of light

The group velocity of light in the presence of linear dispersion ${\frac {dn}{d\omega }}$ is given by [Harris and Han, PRC 82, 4611 (1999)]

$v_{g}={\frac {c}{1+\omega {\frac {dn}{d\omega }}}}$ for light at frequency $\omega$.

A strong linear dispersion with positive slope near EIT then corresponds to very slow light.

Image

As $n=1\rightarrow$, the electric field is unchanged so the power per area

${\frac {P}{A}}={\frac {1}{2}}\epsilon _{o}C|E|^{2}$ also remains unchanged.

Due to slowed group velocity, the pulse is compressed in the medium. As a consequence, the energy density is increased, and the light is partly in the form of an atomic excitation (coherent superposition of the ground states, although most of the energy is exchanged to the control field).

Image

For sufficiently small $\omega _{2}$, the velocity of light may be very small, down to a few m/s [L.V. Hau, S.E. Harris et al., Nature 397, 594 (1999)], as observed in a BEC. Reduced group velocity can also be observed in room-temperature experiment if the setup is Doppler free (co-propagating probe and control fields $\omega _{1}$ and $\omega _{2}$) (otherwise only a small velocity class satisfies the two-photon resonance condition).

If we change control field adiabatically while the pulse is inside the medium, we can coherently stop light, i.e. convert it into an atomic excitation or spin wave. With the reverse process we can then convert the stored spin-wave back into the original light field. The adiabatic conversion is made possible by the finite splitting between bright and dark states. In principle, all coherence properties and other (qm) features of the light are maintained, and it is possible to store non-classical states of light by mapping photon properties one-to-one onto quantized spin waves. More about these quanta called "dark-state polaritons" once we have introduced Dicke states. Is it possible to make use of EIT for, e.g. atom detection without absorption? Answer: no improvement for such linear processes. However: improvement for non-linear processes is possible.

Superradiance

Assume that two identical atoms, one in its ground and the other in its excited state, are placed within a distance $d\gg \lambda _{eg}$ of each other. What happens?

For a simgle atom we have for the emission rate R(t) at time t an emission probability $p(t)=\int _{o}^{t}R(t')dt'$ to have emitted a photon by time t:

$R_{1}(t)=re^{-rt}$

Image

$p_{1}(t)=\int _{o}^{t}dt'R(t')=1-e^{-rt}$ for a single atom

Images

what about two atoms?

Image

It turns out that the correct answer is

$R_{2}(t)=re^{-2pt}$

$p_{2}(t)=\int _{o}^{t}R_{2}(t')dt'={\frac {1}{2}}(1-e^{-2rt})$

Images

The photon is emitted with the same initial rate, but has only probability ${\frac {1}{2}}$ of being emitted at all! How can we understand this? The interaction Hamiltonian is

$V=-{\vec {d}}_{1}\cdot {\vec {E}}({\vec {\gamma }},t)-{\vec {d}}_{2}\cdot {\vec {E}}({\vec {\gamma }},t)=-{\vec {D}}\cdot {\vec {E}}({\vec {\gamma }},t)$ class.

$V=\hbar g(\sigma _{1}^{+}+\sigma _{1}^{-})(a+a^{+})g(\sigma _{2}^{+}+\sigma _{2}^{-})(a+a^{+})QED$ $=\hbar g((\sigma _{1}^{+}+\sigma _{2}^{+}+\sigma _{1}^{-}+\sigma _{2}^{-})(a+a^{+})$ $=\hbar g(\Sigma ^{+}+\Sigma ^{-})(a+a^{+})$

with $\Sigma ^{\pm }{\dot {\Sigma }}_{i=1}^{z}\sigma _{i}^{\pm },{\vec {D}}=\Sigma _{i=1}^{z}{\vec {d}}_{i}$