Difference between revisions of "Atoms in electric fields"
imported>Wikibot m |
imported>Wikibot m |
||
| Line 24: | Line 24: | ||
We require that this operator in unitary and that it has the following key property (or, perhaps more precisely we define the operator through) | We require that this operator in unitary and that it has the following key property (or, perhaps more precisely we define the operator through) | ||
:<math> | :<math> | ||
| + | \pi^\dagger \vec{x} \pi = - \vec{x} | ||
</math> | </math> | ||
which implies | which implies | ||
| Line 199: | Line 200: | ||
<math>H_{mm}^\prime = 0</math> so | <math>H_{mm}^\prime = 0</math> so | ||
the first order perturbation vanishes. To second order, the energy | the first order perturbation vanishes. To second order, the energy | ||
| − | is | + | is given by |
| − | given by | ||
:<math> | :<math> | ||
| − | E_n = E_n^{(0)} - e^2 \mathcal{E}^2 \sum_{m} \mbox{}^\prime \frac{| | + | E_n = E_n^{(0)} - e^2 \mathcal{E}^2 \sum_{m} \mbox{}^\prime \frac{| \langle m | z| n \rangle |^2}{E_m - E_n} |
| − | m | z| n \rangle |^2}{E_m - E_n} | ||
</math> | </math> | ||
If we compare this results with the potential energy of a charge | If we compare this results with the potential energy of a charge | ||
| Line 211: | Line 210: | ||
polarizability in state <math>n</math> is given by | polarizability in state <math>n</math> is given by | ||
:<math> | :<math> | ||
| − | \alpha_n = 2e^2 \ | + | \alpha_n = 2e^2 \sum'_{m} \frac{| \langle m| z | n {\rangle}|^2}{E_m - E_n} |
| − | - E_n} | ||
</math> | </math> | ||
Note that this has the dimensions of length<math>^3</math>, i.e. volume. | Note that this has the dimensions of length<math>^3</math>, i.e. volume. | ||
The induced dipole moment can be found from the polarization. | The induced dipole moment can be found from the polarization. | ||
:<math> | :<math> | ||
| − | d= \alpha \mathcal{E} \hat{z} = 2 e^2 \mathcal{E}\hat{z} | + | d= \alpha \mathcal{E} \hat{z} = 2 e^2 \mathcal{E}\hat{z} \sum'_{m} \frac{| \langle m | z | n {\rangle}|^2}{E_m - E_n} |
| − | \ | ||
| − | |||
</math> | </math> | ||
An alternative way to calculate the dipole moment is to calculate | An alternative way to calculate the dipole moment is to calculate | ||
| Line 350: | Line 346: | ||
(0) = 0</math>. Substituting in Eq.\ \ref{EQ_atomoef7} and integrating | (0) = 0</math>. Substituting in Eq.\ \ref{EQ_atomoef7} and integrating | ||
from <math>t^\prime = 0</math> to <math>t</math> gives | from <math>t^\prime = 0</math> to <math>t</math> gives | ||
| − | <math> | + | :<math>\begin{array}{rcl} |
| − | |H^\prime (t^\prime ) | + | a_k^{(1)} (t) &=& (i\hbar )^{-1} \int_{0}^{t} dt^\prime \langle k |H^\prime (t^\prime ) |g \rangle e^{i\omega_{kg}t^\prime } |
| − | |g \rangle e^{i\omega_{kg}t^\prime } | + | |
| − | + | \\ | |
| − | e} \cdot | + | &=& - (i\hbar )^{-1} \langle k |\hat{e} \cdot D |g \rangle \frac{\mathcal{E}}{2} \int_{0}^{t} dt^\prime {\left[ e^{i(\omega_{kg} + \omega )t^\prime } + e^{i(\omega_{kg} - \omega )t^\prime } \right]} |
| − | D | + | |
| − | e^{i(\omega_{kg} + \omega )t^\prime } + | + | \\ |
| − | e^{i(\omega_{kg} - \omega )t^\prime } \right]} | + | &=& \frac{\mathcal{E}}{2\hbar} \langle k |\hat{e} \cdot D |g \rangle {\left[ \frac{e^{i(\omega_{kg} +\omega )t}-1}{\omega_{kg} + \omega} + \frac{e^{i(\omega_{kg} - \omega )t}-1}{\omega_{kg}-\omega} \right]} |
| − | + | \end{array}</math> | |
| − | = \frac{\mathcal{E}}{2\hbar} \langle k |\hat{e} \cdot D |g | ||
| − | \rangle {\left[ \frac{e^{i(\omega_{kg} +\omega | ||
| − | )t}-1}{\omega_{kg} + \omega} + \frac{e^{i(\omega_{kg} - \omega | ||
| − | )t}-1}{\omega_{kg}-\omega} \right]} | ||
| − | </math> | ||
The -1 terms in the square bracketed term arises because it is | The -1 terms in the square bracketed term arises because it is | ||
assumed that the field was turned on | assumed that the field was turned on | ||
Revision as of 22:12, 27 February 2009
donewcmd error! no pattern match \newcommand{\QU}[1]{\par%
Contents
Atoms in Electric Fields
\markboth{Physics 165, Spring 2003}{Atoms in Electric Fields}
This section deals with how atoms behave in static electric fields. The method is straightforward, involving second order Rayleigh-Schrodinger perturbation theory. The treatment describes the effects of symmetry on the basic interaction, polarizability, and the concept of oscillator strength. Let us review the concept of parity. Parity is a consequence of space inversion.
We propose an operator that (in the spirit of the rotation operator introduced earlier) takes an initial ket and returns a ket with the above inversion operation performed.
We require that this operator in unitary and that it has the following key property (or, perhaps more precisely we define the operator through)
which implies
To put the finest point on it, is an eigenket of with eigenvalue of . Finally, the eigenvalues of are and
Position is "odd" under space inversion or "odd under the parity operator". Angular momentum, on the other hand is even.
Because of this property position and momentum are called vectors or polar vectors and angular momentum is called an axial or psuedo vector. What about wavefunction? What does the parity operator do to wavefunctions? Well it depends on the wavefunction. For example, consider the spherical harmonics (the angular part of the hydrogen atom eigenstates). Some of the wavefunctions are odd under parity and some are even. (In one dimension a cosine wave is "even" whereas a sine wave is "odd".)
Now, consider the case where a state is an energy eigenket and the parity operator commutes with Hamiltonian. Such a ket is not necessarily an eigenket of the parity operator. Consider, for example, the case of the hydrogen atom for . Neglecting higher order pertubations to the hamiltonian, can be made up of a combination of two eigenkets with different parities,
Without any degeneracies eigenstates of the hamiltonian are indeed eigenstates of the parity operator if the hamiltonian and commute. This idea of parity gives rise to what is called a selection rule. Selection rules, in general, are nothing more than the statement that certain operators connect certain states ( for certain ) and do not connect other states (that is, for certain ). Consider, for example, the operator and two different parity eigenstates,
then
One can see this in the following way
which can be true only if . is an "parity odd operator" and it connects states of opposite parity. "Even operators" connect states of the same parity.
Atoms in a Static Electric Field
We can use this basic idea in understanding the problem of an atom subjected to an electric field. We begin by writing down the potential due to a collection of charges,
where
where is the charge distribution. is the total charge, are the dipole moments, are the quadrupole moments, etc. The energy of an overall neutral collection of charges in an electric field can similarly be expanded as
where is the dipole and is the polarizability. Now we are in a better position to solve the problem of the hydrogen atom in a static electric field, , just about the simplest example. The hamiltonian for this problem can be written
where is the "unperturbed" hamiltonian for the hydrogen atom. We chose to solve this via matrix methods. The first step is to write down the matrix elements for the hamiltonian is a basis of our choosing. Let's try with the basis kets, the eigenkets of . So, only contributes diagonal elements to the matrix, . As and are scalars, not operators, we need only consider the effect of . First, is a parity odd operator, connecting only states of different parity. Thus contributes nothing to the diagonal entries nor to any entries with the same angular momentum, . States of the same parity but whose angular momentum differ by more than also result in zero because ... Finally, also only connects states of the same . One can see this by noting that
which is an even function in . Any states differing by would then result in an integral of two even functions (one of those being the originating from the ) and an odd function in which is zero. This resulta can also be seen directly by noting a result of the Wigner-Eckhart theorem that where is just a number. Thus, we produce the "selection rules" for the operator,
NOTE that this strictly applies only the this specific operator. If were pointing in some other direction then things might (and do) change. The matrix for the our hamiltonian reads then
where the entries arranged in order. The 0's are designated with an indication of "why" those particular entries in the matrix are zero, meaning even/odd ( selection rule) and meaning parity ( selection rule. As mentioned above, the contribution to the diagonal elements is zero due to parity. Because the states are degenerate, degenerate pertubation theory must be used to solve the problem. Of course we know that in reality the problem is more complex than this. Both fine, hyperfine and the Lamb shift have been neglected. Solving the problem taking this into account would indicate the use of second order pertubation theory. To see how this all shakes out, let's go ahead and apply pertubation theory directly.
If one is in the case where this simple pertubation theory does not work because of degenerate states (leading to in the denominator then it is best just to diagonalize the Hamiltonian in relation to . If you do that for the case of you find that the eigenstates are
where is a constant. The last two states have a linear response to the electric field, or a linear Stark effect. Even is there were a small splitting between the different states in the manifold, if the field interaction were higher that the splitting then there would be also be a linear Stark effect. At lower fields the interaction would be second order (second order pertubation theory would be called for) and the response would be quadratic in the applied electric field. Notice the the new eigenstates are a mixture of states of different parity. This mixture allows for a dipole to be formed and it is the interaction of the electic field with this dipole that gives rise to a linear response to the field. It is this dipole that is talked about by chemists when they say that a molecule "has a dipole moment". Molecules "have dipole moments" because they have closely lying states of opposite parity so small fields put them in the linear Stark regime. But make no mistake, at low enough fields, the response would be quadratic, just as it is in the case of atoms. Now, all of this has been talked about under the (essentially correct) assumption that and, therefore, that the eigenstates of the H atom are also parity eigenstates. But what if ? This occurs when the weak force is involved and will likely be present in nature and described, eventually, by extensions to the Standard Model. Such mechanisms can lead to the presence of permanent electic dipole moments of elementary particles.
Some Results of Stationary Perturbation Theory
For reference, we recapitulate some elementary results from perturbation theory. Assume that the Hamiltonian of a system may be written as the sum of two parts
and that the eigenstates and eigenvalues of are known:
If it is not possible to find the eigenvalues of exactly, it is possible to write power series expressions for them that converge over some interval. If is time independent, the problem is stationary and the appropriate perturbation theory is Rayleigh- Schrodinger stationary state perturbation theory, described in most texts in quantum mechanics. We write
and express the order perturbation in terms of and . The energies are given by
We shall only use the lowest two orders here. The first order results are
- Failed to parse (syntax error): {\displaystyle | n^{(1)} \rangle = \sum_{m} \mbox{}^\prime \frac{| m \rangle \langle m | H^\prime | n {\rangle}}{E_n - E_m} }
The symbol indicates that the term is excluded. It is understood that the sum extends over continuum states. Note that the state function is nor properly normalized, but that the error is quadratic in . The second order results are Failed to parse (syntax error): {\displaystyle <math> E_n^{(2)} = \sum_{n} \mbox{}^\prime \frac{ | \langle m | H^\prime | n {\rangle} |^2}{E_n - E_m} } </math>
- Failed to parse (syntax error): {\displaystyle | n^{(2)} {\rangle}= \sum_{m} \mbox{}^\prime | m \rangle {\left[\frac{ \langle m | H^\prime | n {\rangle}}{E_n-E_m}{\left[1-\frac{ \langle n| H^\prime | n {\rangle}}{E_n - E_m} \right]} + \sum_{p} \mbox{}^\prime \frac{ \langle m| H^\prime | p \rangle \langle p | H^\prime | n {\rangle}}{(E_n -E_m)(E_n-E_p)}\right]} }
In second order perturbation theory the effect of a coupling of and by is to push the levels apart, independent of the value of . Consequently, states coupled by always repel each other.
Perturbation Theory of Polarizability
We turn now to finding the energy and polarizability of an atom in a static field along the +z direction. We apply perturbation theory taking to describe the unperturbed atomic system and
As discussed in Sect.\ \ref{SEC_rp}, parity requires that so the first order perturbation vanishes. To second order, the energy is given by
- Failed to parse (syntax error): {\displaystyle E_n = E_n^{(0)} - e^2 \mathcal{E}^2 \sum_{m} \mbox{}^\prime \frac{| \langle m | z| n \rangle |^2}{E_m - E_n} }
If we compare this results with the potential energy of a charge distribution interacting with an electric field, (Eq.\ \ref{EQ_aefone}), we can identify the polarizability interaction with the second term in this equation. As a result the polarizability in state is given by
Note that this has the dimensions of length, i.e. volume. The induced dipole moment can be found from the polarization.
An alternative way to calculate the dipole moment is to calculate the expectation value of the dipole operator, Eq.\ \ref{EQ_aefthree}, using the first order perturbed state vector.
where the sum is over Only the term will contribute, and it will yield an interaction energy in agreement with Eq.\ \ref{EQ_polartwo}. As an example, for the ground state of hydrogen we can obtain a lower limit for the polarizability by considering only the contribution to the sum of the state. Values for the various moments in hydrogen are given in Bethe and Salpeter, Section 63. Using = 1.666, and , we obtain atomic units (i.e. ). The polarizability of the ground state of hydrogen can be calculated exactly. It turns out that the state makes the major contribution, and that the higher bound states contribute relatively little. However, the continuum makes a significant contributions. The exact value is 4.5. To put this polarizability in perspective, note that the potential of a conducting sphere of radius in a uniform electric field is given by
The induced dipole moment is , so that the polarizability is . For the ground state of hydrogen, , so to a crude approximation, in an electric field hydrogen behaves like a conducting sphere. Polarizability may be approximated easily, though not accurately, using Unsold's approximation in which the energy term in the denominator of Eq.\ \ref{EQ_polarsix} is replaced by an average energy interval . The sum can then be evaluated using the closure rule . (Note that the term does not need to be excluded from the sum, since .). With this approximation,
For hydrogen in the ground state, . If we take the average excitation energy to be , the result is .
Atoms in an Oscillating Electric Field
There is a close connection between the behavior of an atom in a static electric field and its response to an oscillating field, i.e. a connection between the Stark effect and radiation processes. In the former case, the field induces a static dipole moment; in the latter case, it induces an oscillating moment. An oscillating moment creates an oscillating macroscopic polarization and leads to the absorption and emission of radiation. We shall calculate the response of an atom to an oscillating field
where is the polarization vector for the field. For a weak field the time varying state of this system can be found from first order time dependent perturbation theory. We shall write the electric dipole operator as D = -er. (This is a change of notation. Previously the symbol was d.) The Hamiltonian naturally separates into two parts, , where is the unperturbed Hamiltonian and
We shall express the solution of the time dependent Schroedinger equation in terms of the eigenstates of .
where . Because of the perturbation , the 's become time dependent, and we have
Left multiplying the final two expressions by to project out the -th terms yields
where . In perturbation theory, this set of equations is solved by a set of approximations to labeled . Starting with
one sets
and solves for the successive approximations by integration. We now apply this to the problem of an atom which is in its ground state at , and which is subject to the interaction of Eq.\ \ref{EQ_atomoef2}. Consequently , . Substituting in Eq.\ \ref{EQ_atomoef7} and integrating from to gives
The -1 terms in the square bracketed term arises because it is assumed that the field was turned on instantaneously at . They represent transients that rapidly damp and can be neglected. The term with , in the denominator is the counter-rotating term. It can be neglected if one is considering cases where (i.e. near resonance), but we shall retain both terms and calculate the expectation value of the first order time dependent dipole operator </math>
If we consider the case of linearly polarized light , then
We can write in terms of a polarizability :
This result diverges if . Later, when we introduce radiative damping, the divergence will be avoided in the usual way.
Oscillator Strength
Eq.\ \ref{EQ_atomoef11} resemble the oscillating dipole moment of a system of classical oscillators. Consider a set of oscillators having charge , mass , and natural frequency , driven by the field . The amplitude of the motion is given by
If we have a set of such oscillators, then the total oscillating moment is given by
This is strongly reminiscent of Eq.\ \ref{EQ_atomoef10}. It is useful to introduce the concept of oscillator strength, a dimensionless quantity defined as
where and are any two eigenstates. Note that is positive if , i.e. for absoprtion, and negative if Then, Eq.\ \ref{EQ_atomoef10} becomes
Comparing this with Eq.\ \ref{EQ_ostre2}, we see that the behavior of an atom in an oscillating field mimics a set of classical oscillators with the same frequencies as the eigenfrequencies of the atom, but having effective charge strengths .\\ The oscillator strength is useful for characterizing radiative interactions and also the susceptibiltiy of atoms. It satisfies an important sum rule, the Thomas-Reiche-Kuhn sum rule:
We prove by considering the general Hamiltonian
Using the commutator relation
and the relation , we have
where , and . However,
Consequently,
where . Thus, we can write Eq.\ \ref{EQ_ostre3} in either of two forms:
Taking half the sum of these equations and using the closure relation , we have
We have calculated this for a one-electron atom, but the application to a Z-electron atom is straightforward because the Hamiltonian in Eq.\ \ref{EQ_ostre6} is quite general. In this case
Here is some eigenstate of the system, and the index describes all the eigenstates of all the electrons -- including continuum states. In cases where only a single electron will be excited, however, for instance in the optical regime of a "single-electron" atom where the inner core electrons are essentially unaffected by the radiation, the atom behaves as if it were a single electron system with . Note that is positive if , i.e. if the final state lies above the initial state. Such a transition corresponds to absorption of a photon. Since , the oscillator strength for emission of a photon is negative. Our definition of oscillator strength, Eq.\ \ref{EQ_ostre3}, singles out a particular axis, the -axis, fixed by the polarization of the light. Consequently, it depends on the orientation of the atom in the initial state and final states. It is convenient to introduce the average oscillator strength (often simply called the oscillator strength), by letting , summing over the initial state and averaging over the final state.\\
(This is the conversion followed by Sobelman.) It is evident that
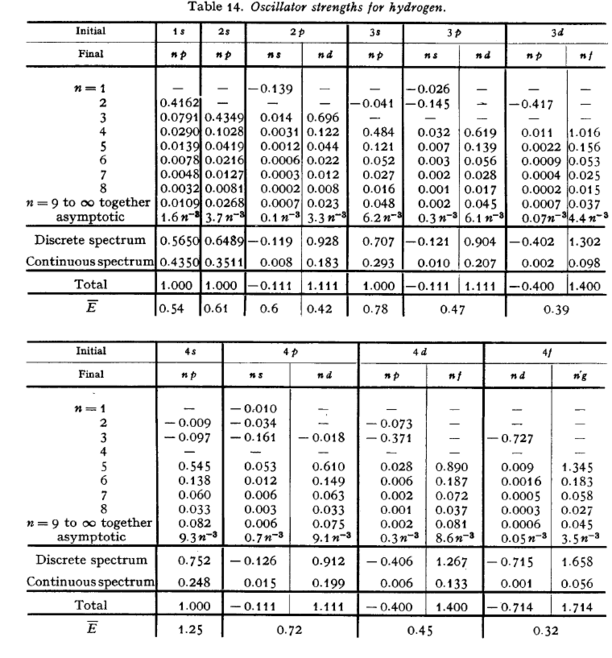
where is the multiplicity factor for state . An extensive discussion of the sum rules and their applications to oscillator strengths and transition momentums can be found in Bethe and Salpeter, section 6.1. Among the interesting features they point out is that transitions from an initial state to a final state on the average have stronger oscillator strengths for absorption if , and stronger oscillator strengths for emission if . In other words, atoms "like" to increase their angular momentum on absorption of a photon, and decrease it on emission. The following page gives a table of oscillator strengths for hydrogen in which this tendency can be readily identified. (Taken from {\it The Quantum Mechanics of One- and Two-Electron Atoms}, H.A. Bethe and E.E. Salpeter, Academic Press (1957).) \begin{figure}[htbp]
\caption{ Oscillator strengths for hydrogen. From Mechanics of One- and Two-Electron Atoms} \end{figure}






























































![{\displaystyle [H,\pi ]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d99e762688b1c8240c972dfa4261c1cc7d6b00)
![{\displaystyle [H,\pi ]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdb19cc8d69e390bef7de1f0970c8d5bb991b618)




















![{\displaystyle =2{\rm {Re}}[\langle n^{(0)}|d|n^{(1)}\rangle ]=2e^{2}{\rm {Re}}{\left[\sum _{s,m}{\frac {\langle n^{(0)}|s|m\rangle \langle m|z|n^{(0)}\rangle }{E_{m}-E_{n}}}\right]}{\hat {s}}\cdot {\hat {z}}{\mathcal {E}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afd33952a21990436ab03840a4b4e1e286b70684)












































![{\displaystyle {\begin{array}{rcl}a_{k}^{(1)}(t)&=&(i\hbar )^{-1}\int _{0}^{t}dt^{\prime }\langle k|H^{\prime }(t^{\prime })|g\rangle e^{i\omega _{kg}t^{\prime }}\\&=&-(i\hbar )^{-1}\langle k|{\hat {e}}\cdot D|g\rangle {\frac {\mathcal {E}}{2}}\int _{0}^{t}dt^{\prime }{\left[e^{i(\omega _{kg}+\omega )t^{\prime }}+e^{i(\omega _{kg}-\omega )t^{\prime }}\right]}\\&=&{\frac {\mathcal {E}}{2\hbar }}\langle k|{\hat {e}}\cdot D|g\rangle {\left[{\frac {e^{i(\omega _{kg}+\omega )t}-1}{\omega _{kg}+\omega }}+{\frac {e^{i(\omega _{kg}-\omega )t}-1}{\omega _{kg}-\omega }}\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d5e4872c67deeb9e95cc30b7f74ecd1122ce0f)




![{\displaystyle ={\mathcal {E}}{\rm {Re}}{\left[\sum _{k}{\frac {\langle g|D|k\rangle \langle k|{\hat {e}}\cdot D|g\rangle }{\hbar }}{\left\{{\frac {e^{i\omega t}}{\omega _{kg}+\omega }}+{\frac {e^{-i\omega t}}{\omega _{kg}-\omega }}\right\}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53af062c95a695df7be702736d975858fabc3b09)




















![{\displaystyle [A,B^{2}]=[A,B]B+B[A,B],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e16bcf41c2c00f41091a8b2f6ec1a54c3c26aa3)
![{\displaystyle [r_{j},p_{k}]=i\hbar \delta _{jk}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47639ff8ac69b050c5dc9d8cf58f9c6d17af6a3)
![{\displaystyle [r,H]={\frac {i\hbar }{m}}p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/335156c1e95f556b5ff6979d61bd8c1ef0ea7263)


![{\displaystyle \langle j|[r,H]|k\rangle =(E_{k}-E_{n})\langle j|r|k\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4756f9f0266fc68ae7c3ce2a7995ae930e09add7)




![{\displaystyle \sum _{k}f_{kj}={\frac {i}{\hbar }}{\left[\langle j|p_{z}z-zp_{z}|j\rangle \right]}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9256c4cbcfdc8f1d87d37c52474b7279a2ec1990)