Difference between revisions of "Laser cooling of trapped ions"
imported>Ichuang |
imported>R landig |
||
| Line 1: | Line 1: | ||
| − | |||
A simple comparison of potential depths provides useful perspective | A simple comparison of potential depths provides useful perspective | ||
| Line 134: | Line 133: | ||
\\ | \\ | ||
&=& \frac{\hbar\Omega}{2} \left[ { S_+ + S_- } \right] | &=& \frac{\hbar\Omega}{2} \left[ { S_+ + S_- } \right] | ||
| − | \left[ { e^{i\eta(a+ a^\dagger )-\omega t} + e^{-i\eta(a+ a^\dagger )+\omega t} } \right] | + | \left[ { e^{i\eta(a+ a^\dagger )-i\omega t} + e^{-i\eta(a+ a^\dagger )+i\omega t} } \right] |
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
Revision as of 13:47, 13 May 2009
A simple comparison of potential depths provides useful perspective for understanding the experimental convenience of trapped ions versus neutral atoms. Recall that the depth of a dipole force trap is ; for a Watt laser at m focused to a m waist used to trap atomic sodium, the trap depth is K; this is not much more than the Doppler cooling limit. A magneto-optical trap is much deeper; for typical laboratory magnetic field gradients, depths of K can be obtained. In contrast, a singly charged ion in an electric field of V/mm, which is easily obtained in the laboratory, the depth of an RF ion trap can be over K. This allows hot ions to be readily trapped, and subsequently laser cooled.
A unique aspect of trapped ions, versus neutral atoms, is the importance of the role of the trapping potential in the laser cooling process. As the motion of ions is reduced to the characteristic size of their confining potential, quantum aspects of their motion become accessible. This allows a form of laser cooling known as {\em resolved sideband cooling} to be performed, through which ions can be cooled to their motional ground states.
Contents
Physical system
Two kinds of ion traps are widely used. The Penning trap employs static magnetic and electric fields to confine ions. The Paul trap employs just oscillating electric fields, and is the configuration we shall study here.
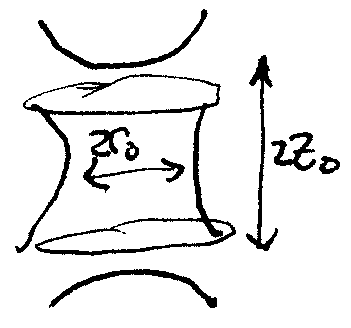
Consider this electrode configuration:
The inner surfaces are hyperboloids, the top and bottom electrodes are tied together, and the drive voltage oscillates sinusoidally at frequency , such that near the center of the electrodes, the potential is
For a singly charged ion of mass located in this trap, the solutions to the equations of motion balancing the force of the electric field against ion motion are
This is a Mathieu equation, where
and is a non-dimensional parameter. When , stable solutions exist. These solutions describe a fast oscillation known as micromotion, superposed on top of a slow harmonic motion with secular frequency
The amplitude of micromotion, in a well designed experiment, is very small, and thus can be neglected. The dominant physics of a trapped ion system are thus described by an atom coupled to a simple harmonic oscillator.
Typically, RF frequencies are MHz or higher, and secular frequencies are MHz. These may be compared with typical spontaneous emission rates of MHz, and the recoil energy from a single photon emission of
where is the frequency of the laser. The three systems involved in this scenario are thus the trapped ion, with its atomic levels, the harmonic oscillator, and incident electromagnetic radiation on the atom. That is, we have a system of atom + photon + phonon, where the phonon represents quantized vibrational modes of the trapped atom.
Hamiltonian: classical field + 2-level atom
Let us model the trapped ion system initially using a classical field, and neglect spontaneous emission. Let us also approximate the atom to be a two-level system. The Hamiltonian for such a system has the interaction
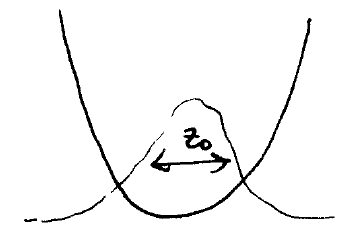
where we use to denote the spin of the atom, and assume the electric field is along the direction. is the position of the ion in the field; we quantize this degree of freedom by representing it as motion in a harmonic oscillator, letting
where is the characteristic length scale of the harmonic motion. The interaction Hamiltonian can thus be written as
The Lamb-Dicke parameter
When the ions are well-confined, a natural small parameter arises, in which this interaction can be expanded. This parameter describes the extent to which the ion is localized in the trap, relative to the incident light. We define this Lamb-Dicke parameter as
It is the ratio of the size of the ground state wavefunction of the motion in the harmonic oscillator, to the incident laser wavelength:
\noindent Note that can also be understood as being the ratio of the recoil frequency to the vibrational frequency.
Expansion in the Lamb-Dicke parameter
Let us now expand to leading order in . Recall that , and let be the Rabi frequency. In terms of these,
The exponentials can be expanded to leading order in , resulting in terms of the form , such that
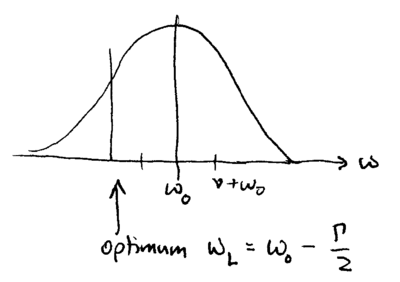
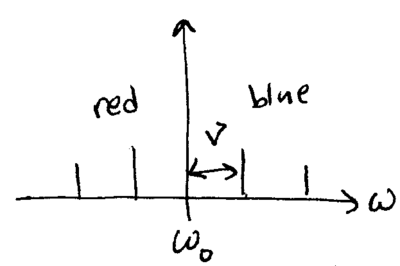
In the above expansion, it is assumed that the laser's frequency is close to that of the atomic transition, such that to good approximation, terms oscillating as can be dropped (the rotating wave approximation). The first term in this expression describes the carrier transition, in which the light changes the internal atomic state, and the second term describes sideband transitions, in which the light changes both the internal atomic state as well as its motional state. These transitions have a frequency spectrum which looks like:
Moving into the rotating frame defined by the atom's internal and motional states simplifies this Hamiltonian, providing a time-independent form. Let this frame be defined by the system Hamiltonian
such that in the rotating frame, operators are transformed according to
The interaction Hamiltonian in this frame is approximated by
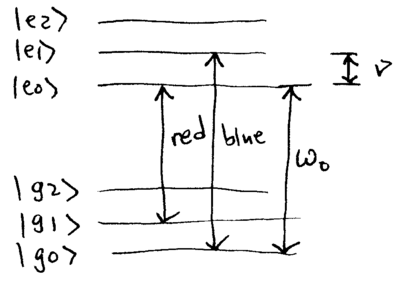
The first few energy levels are diagrammed here:
Resolved sideband cooling
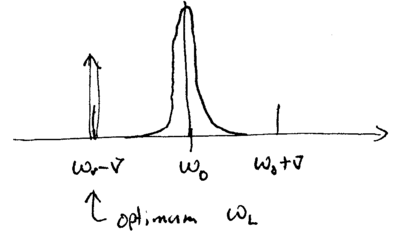
When the ion is hot, doppler shifts will dominate, and the sidebands will be unresolvable. However, for many ions, standard doppler cooling is sufficient to reach the point at which the motional sidebands become resolvable. In that regime, a different cooling method can be applied; this method is known as {\em resolved sideband cooling}.
The basic idea of this method is analogous to optical pumping: the laser is detuned to cause transitions on the red sideband of the ion, removing one quantum of motion for each photon absorbed. Just as for laser cooling of neutral atoms, let us calculate the cooling limit of such a procedure.
Let be an eigenstate of the harmonic motion of the ion, with motional quantum number , and recall that and . The transition amplitude between motional states and is given by this matrix element of the interaction Hamiltonian:
in the limit that is small, and we're interested only in terms which couple and . Let us define
as the lineshape function; it captures the frequency dependent response of the atom to a laser detuned by from the atomic resonance.
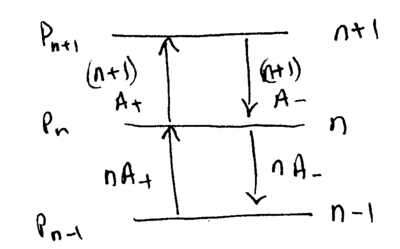
The incident laser light can connect three basic transitions: the carrier, the blue sideband, and the red sideband. How do those transitions contribute to changing the motional quantum number ? Excitations of the carrier transition couple (using ) to the state , with rate proportional to . The excited state can then decay to or , changing the motional quantum number; these transitions occur with rates proportional to and , respectively, where is a geometric factor describing the probability for spontaneous emission to change . For dipole emission into free space, . These transitions are diagrammed as follows:
On the blue and red sidebands, absorption happens at a rate proportional to and , while spontaneous emission happens at rate proportional to , all-together connecting with . These transitions are diagrammed as follows:
To obtain the cooling limits of resolved sideband cooling, we need to write down the rate equations for these phonon-number changing carrier and sideband excitation processes, and solve for the steady state average phonon number. For the transitions
where is the probability of being in the phonon state, the transition rate coefficients are
The first term in the brackets comes from the sideband excitations, and the second from the carrier. The rate equations for the populations are thus
The average phonon number is
which evolves as
This differential equation has a solution in which decays exponentially as to an equilibrium average phonon number ,
The corresponding equilibrium temperature is given by
It is insightful to evaluate these expressions in two limits. When the ion is weakly confined, such that , then the sidebands are poorly resolved:
The optimum detuning is , and cooling corresponds to standard Doppler cooling of free particles, giving
with a final temperature of around
Including geometric factors reduces this slightly, by . The strong confinement limit is reached when , so that individual sidebands are well resolved:
This is the case of resolved sideband cooling, as mentioned above. For this case, the laser is detuned to , such that , and , such that the equilibrium average phonon number, given by
is approximately , which is much less than one. This corresponds to a temperature of
Essentially, the final temperature is set by zero-point motion of the ion in the harmonic trap.






















![{\displaystyle {\begin{array}{rcl}H_{I}&=&{\vec {d}}\cdot {\vec {E}}\\&=&\left[{d{\vec {S}}}\right]\cdot \left[{E{\hat {x}}\cos(kz-\omega t)}\right]\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88b249de14d5e41f788a686b961f174126a5fb03)





![{\displaystyle H_{I}=dES_{x}\cos \left[{kz_{0}(a+a^{\dagger })-\omega t}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e476fd1511b1bd6273cfb45d390b1f2e82fc68a)





![{\displaystyle {\begin{array}{rcl}H_{I}&=&\hbar \Omega \left[{S_{+}+S_{-}}\right]\cos \left[{\eta (a+a^{\dagger })-\omega t}\right]\\&=&{\frac {\hbar \Omega }{2}}\left[{S_{+}+S_{-}}\right]\left[{e^{i\eta (a+a^{\dagger })-i\omega t}+e^{-i\eta (a+a^{\dagger })+i\omega t}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d2fb8a5805b64c7e6a2f9a27657aeee3287f713)
![{\displaystyle \left[{1+i\eta (a+a^{\dagger })}\right]e^{-i\omega t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7909df519a9781fb3d0c7d5ce2a3da6a71fb7281)
![{\displaystyle {\begin{array}{rcl}H_{I}&=&{\frac {\hbar \Omega }{2}}\left[{S_{+}e^{-i\omega t}+S_{-}e^{i\omega t}}\right]+{\frac {i\eta \hbar \Omega }{2}}(S_{+}+S_{-})\left[{a+a^{\dagger }}\right]\left({e^{-i\omega t}-e^{i\omega t}}\right)\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b8afe5bc9450df56aa6ca0332488469e295724)



![{\displaystyle {\begin{array}{rcl}H'_{I}&=&e^{iH_{0}t/\hbar }H_{I}e^{-iH_{0}t/\hbar }\\&=&\left\{{\begin{array}{lr}{\frac {\hbar \Omega }{2}}\left[{S_{+}+S_{-}}\right]&{\omega \approx \omega _{0}~~{\rm {carrier}}}\\{\frac {i\eta \hbar \Omega }{2}}(S_{+}a^{\dagger }-S_{-}a)&{\rm {\omega \approx \omega _{0}+\nu ~~{\rm {blue~sideband}}}}\\{\frac {i\eta \hbar \Omega }{2}}(S_{+}a-S_{-}a^{\dagger })&{\rm {\omega \approx \omega _{0}-\nu ~~{\rm {red~sideband}}}}\end{array}}\right.\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1db71d88513f2a7c304214fb5e816603917f6aa)





![{\displaystyle {\begin{array}{rcl}\langle n\pm 1|H'_{I}|n\rangle \approx \langle n\pm 1|i\eta {\frac {\hbar \Omega }{2}}\left[{{\sqrt {n}}|n-1\rangle \langle n|-{\sqrt {n+1}}|n+1\rangle \langle n|}\right]|n{\rangle }\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8ad44051c6b3e2ebf567acd69789c00dcf090b)













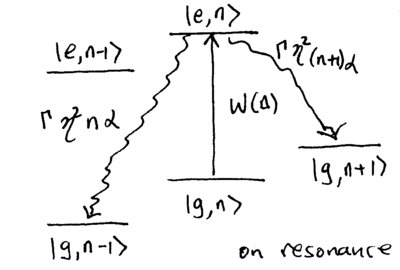




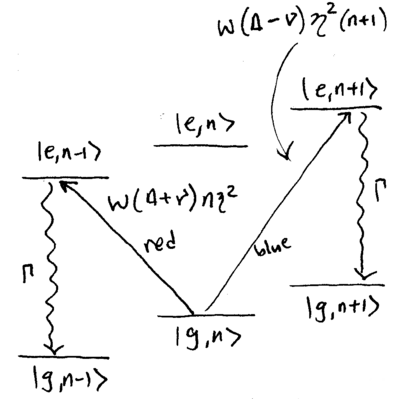

![{\displaystyle A_{\pm }={\frac {\Omega ^{2}}{\Gamma }}\eta ^{2}\left[{W(\Delta \mp \nu )+\alpha W(\Delta )}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ab62623e908476e76e44ad96cf4d0a6aaa32da1)
![{\displaystyle {\dot {P}}_{n}=\left[{nP_{n-1}-(n+1)P_{n}}\right]A_{+}+\left[{(n+1)P_{n+1}-nP_{n}}\right]A_{-}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337f828eb099bccb26dc7a4ac03fff0dc9c52600)


![{\displaystyle {\begin{array}{rcl}{\frac {d}{dt}}{\bar {n}}&=&A_{-}\left[{\sum _{n}n(n+1)P_{n+1}-n^{2}P_{n}}\right]+A_{+}\left[{\sum _{n}n^{2}P_{n-1}-n(n+1)P_{n}}\right]\\&=&-{\bar {n}}A_{-}+({\bar {n}}+1)A_{+}\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23935219ee9f90f22b0c80793cbd3b95297d4240)