Difference between revisions of "Lineshape"
imported>Ichuang |
imported>Wikibot m |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
= Resonance Line Shapes = | = Resonance Line Shapes = | ||
In this chapter, we will discuss several phenomena which affect the line shape. | In this chapter, we will discuss several phenomena which affect the line shape. | ||
| Line 454: | Line 451: | ||
<math>\left|a\right\rangle</math> to state <math>\left|b\right\rangle</math> , then | <math>\left|a\right\rangle</math> to state <math>\left|b\right\rangle</math> , then | ||
:<math> | :<math> | ||
| − | W_{ba} = \frac{d \left| B(t)\right| ^2}{dt} = B^*\dot{B} + \dot{B}^* B = | + | W_{ba} = \frac{d \left| B(t)\right| |
| + | ^2}{dt} = B^*\dot{B} + \dot{B}^* B = | ||
- iB^* \left\langle b\right| V(t) \left|a\right\rangle e^{+i\omega_0 t} A + \text{c.c.} | - iB^* \left\langle b\right| V(t) \left|a\right\rangle e^{+i\omega_0 t} A + \text{c.c.} | ||
</math> | </math> | ||
| Line 488: | Line 486: | ||
Then | Then | ||
:<math> | :<math> | ||
| − | G_{ba} (\tau ) = \frac{ \left| x\right| ^2}{4} e^{+i\omega \tau}, | + | G_{ba} (\tau ) = \frac{ \left| x\right| |
| + | ^2}{4} e^{+i\omega \tau}, | ||
</math> | </math> | ||
and | and | ||
:<math> | :<math> | ||
| − | W_{ba} = \frac{ \left| x\right| ^2}{4} \int_{-t}^{+t} e^{-i( \omega_0 | + | W_{ba} = \frac{ \left| x\right| |
| − | -\omega ) \tau} d\tau = \frac{ \left| x\right| ^2}{2} \frac{\sin (\omega_0 | + | ^2}{4} \int_{-t}^{+t} e^{-i( \omega_0 |
| + | -\omega ) \tau} d\tau = \frac{ \left| x\right| | ||
| + | ^2}{2} \frac{\sin (\omega_0 | ||
- \omega ) t}{(\omega_0 - \omega )} | - \omega ) t}{(\omega_0 - \omega )} | ||
</math> | </math> | ||
| Line 552: | Line 553: | ||
population of atoms in state <math>b</math> varies as | population of atoms in state <math>b</math> varies as | ||
:<math> | :<math> | ||
| − | N(t) = N_0 \left| \Psi_b (t)\right| | + | N(t) = N_0 \left| \Psi_b (t)\right| ^2 |
| + | = N_0 e^{-\gamma_b t} | ||
</math> | </math> | ||
as we surmised. Making this {\it ansatz}, the dipole matrix element | as we surmised. Making this {\it ansatz}, the dipole matrix element | ||
| Line 563: | Line 565: | ||
state of the system, then <math>\gamma_a = 0</math> and <math>\Gamma =\gamma_b </math>.) We have | state of the system, then <math>\gamma_a = 0</math> and <math>\Gamma =\gamma_b </math>.) We have | ||
:<math> | :<math> | ||
| − | G_{ba} (\tau ) = \frac{ \left| x\right| ^2}{4} e^{-\Gamma \ | + | G_{ba} (\tau ) = \frac{ \left| x\right| |
| + | ^2}{4} | ||
| + | e^{-\Gamma \left| \tau\right| | ||
| + | }/2 e^{i\omega \tau} | ||
</math> | </math> | ||
From Equation \ref{EQ_cof3}, we have | From Equation \ref{EQ_cof3}, we have | ||
:<math> | :<math> | ||
| − | W_{ba} = \frac{ \left| x\right| ^2}{4} \int_{-\infty}^{\infty} e^{-\Gamma \left| \tau\right| /2} | + | W_{ba} = \frac{ \left| x\right| |
| − | e^{-i(\omega_0 - \omega )\tau} d\tau = \frac{ \left| x\right| ^2}{2} | + | ^2}{4} \int_{-\infty}^{\infty} e^{-\Gamma \left| \tau\right| |
| + | /2} | ||
| + | e^{-i(\omega_0 - \omega )\tau} d\tau = \frac{ \left| x\right| | ||
| + | ^2}{2} | ||
\frac{ \frac{\Gamma}{2}}{{\left( \frac{\Gamma}{2} \right)^2} + | \frac{ \frac{\Gamma}{2}}{{\left( \frac{\Gamma}{2} \right)^2} + | ||
{\left( \omega - \omega_0 \right)^2}} | {\left( \omega - \omega_0 \right)^2}} | ||
| Line 575: | Line 583: | ||
the linewidth <math>\Gamma</math>, does not depend on the power. In this first | the linewidth <math>\Gamma</math>, does not depend on the power. In this first | ||
order treatment, saturation does not occur. | order treatment, saturation does not occur. | ||
| − | |||
== Doppler broadening == | == Doppler broadening == | ||
Consider a gas of atoms moving freely, irradiated by an electromagnetic plane | Consider a gas of atoms moving freely, irradiated by an electromagnetic plane | ||
| Line 591: | Line 598: | ||
If the atoms are moving, then | If the atoms are moving, then | ||
:<math> | :<math> | ||
| − | G_{ba} = \frac{ \left| x\right| ^2}{4} e^{i\omega (t^\prime-t)} | + | G_{ba} = \frac{ \left| x\right| |
| + | ^2}{4} e^{i\omega (t^\prime-t)} | ||
\overline{e^{ik(z(t^\prime ) - z (t))}} | \overline{e^{ik(z(t^\prime ) - z (t))}} | ||
</math> | </math> | ||
| Line 617: | Line 625: | ||
so that | so that | ||
:<math> | :<math> | ||
| − | G(t) = \frac{ \left| x\right| ^2}{4} e^{-(k\alpha \tau )^2/4} e^{i\omega \tau} | + | G(t) = \frac{ \left| x\right| |
| + | ^2}{4} e^{-(k\alpha \tau )^2/4} e^{i\omega \tau} | ||
</math> | </math> | ||
Equation \ref{EQ_cof3} becomes | Equation \ref{EQ_cof3} becomes | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | W_{ba} &= \frac{ \left| x\right| ^2}{4} \int_{- \infty}^{\infty} | + | W_{ba} &= \frac{ \left| x\right| |
| + | ^2}{4} \int_{- \infty}^{\infty} | ||
e^{-(k\alpha \tau )^2/4} e^{i(\omega - \omega_0 )\tau} | e^{-(k\alpha \tau )^2/4} e^{i(\omega - \omega_0 )\tau} | ||
d\tau \\ | d\tau \\ | ||
| − | &= \frac{ \left| x\right| ^2}{2} \frac{1}{k \alpha} e^{-( (\omega - \omega_0) / | + | &= \frac{ \left| x\right| |
| + | ^2}{2} \frac{1}{k \alpha} e^{-( (\omega - \omega_0) / | ||
k\alpha)^2} | k\alpha)^2} | ||
| Line 758: | Line 769: | ||
The transition rate is | The transition rate is | ||
:<math> | :<math> | ||
| − | R \propto | + | R \propto |{ \left\langle \psi_f^\text{trap}\right| e^{-i {\bf{k}} \cdot {\bf{r}} } |
| − | \left|\psi_i^\text{trap}\right\rangle }^2 | + | \left|\psi_i^\text{trap}\right\rangle }|^2 |
</math> | </math> | ||
If the matrix element is evaluated in the momentum representation | If the matrix element is evaluated in the momentum representation | ||
<math>e^{-i {\bf{k}} \cdot {\bf{r}} }</math> is a translation operator (by <math>-\hbar {\bf{k}} </math>) | <math>e^{-i {\bf{k}} \cdot {\bf{r}} }</math> is a translation operator (by <math>-\hbar {\bf{k}} </math>) | ||
| − | so this factor becomes <math> | + | so this factor becomes <math>|{\braket{\phi_f( {\bf{p}} - \hbar |
| − | {\bf{k}} )}{\phi_i( {\bf{p}} }}^2</math>. In the case of a harmonic oscillator with <math>n_i | + | {\bf{k}} )}{\phi_i( {\bf{p}} }}}|^2</math>. In the case of a harmonic oscillator with <math>n_i |
, n_f \gg 1</math>, the confinement factor will yield the Bessel function expression | , n_f \gg 1</math>, the confinement factor will yield the Bessel function expression | ||
consistent with Equation \ref{EQ_soe6}. | consistent with Equation \ref{EQ_soe6}. | ||
| Line 842: | Line 853: | ||
<math>z^\prime</math>, assuming that at <math>t = 0</math> it was at <math>z</math>, is | <math>z^\prime</math>, assuming that at <math>t = 0</math> it was at <math>z</math>, is | ||
:<math> | :<math> | ||
| − | P(z^\prime , z, t) = \frac{1}{\sqrt{4\pi D \left| t\right| }} e^{-(z^\prime - z)^2/4 | + | P(z^\prime , z, t) = \frac{1}{\sqrt{4\pi D \left| t\right| |
| − | D \left| t\right| } | + | }} e^{-(z^\prime - z)^2/4 |
| + | D \left| t\right| | ||
| + | } | ||
</math> | </math> | ||
where <math>D</math> is the diffusion constant. Writing <math>z^\prime - z = s</math> we need | where <math>D</math> is the diffusion constant. Writing <math>z^\prime - z = s</math> we need | ||
to evaluate | to evaluate | ||
:<math> | :<math> | ||
| − | G_{ba} = \frac{ \left| x\right| ^2}{4} \overline{ e^{-iks}} e^{i\omega\tau} | + | G_{ba} = \frac{ \left| x\right| ^2 |
| − | = \frac{ \left| x\right| ^2}{4} \frac{e^{i \omega\tau}}{\sqrt{4\pi D \left| \tau\right| }} | + | }{4} \overline{ e^{-iks}} e^{i\omega\tau} |
| − | \int_{-\infty}^{\infty} e^{-s^2/4 D \left| \tau\right| } e^{-iks} ds | + | = \frac{ \left| x\right| ^2 |
| − | = \frac{ \left| x\right| ^2}{4} e^{-k^2D \left| \tau\right| } e^{i\omega\tau} | + | }{4} \frac{e^{i \omega\tau}}{\sqrt{4\pi D \left| \tau\right| |
| + | }} | ||
| + | \int_{-\infty}^{\infty} e^{-s^2/4 D \left| \tau\right| | ||
| + | } e^{-iks} ds | ||
| + | = \frac{ \left| x\right| ^2 | ||
| + | }{4} e^{-k^2D \left| \tau\right| | ||
| + | } e^{i\omega\tau} | ||
</math> | </math> | ||
Then | Then | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | W_{ba} &= \frac{ \left| x\right| ^2}{4} \int_{-\infty}^{\infty} e^{-k^2 D \left| \tau\right| } | + | W_{ba} &= \frac{ \left| x\right| ^2 |
| + | }{4} \int_{-\infty}^{\infty} e^{-k^2 D \left| \tau\right| | ||
| + | } | ||
e^{-i(\omega_0 - \omega )\tau} d\tau \\ | e^{-i(\omega_0 - \omega )\tau} d\tau \\ | ||
| − | &= \frac{ \left| x\right| ^2}{4} 2\text{Re} \left\{ \frac{1}{k^2 D+ i (\omega_0 - \omega )}\right\} \\ | + | &= \frac{ \left| x\right| ^2 |
| − | &= \frac{ \left| x\right| ^2}{2} \frac{k^2D}{(k^2D)^2 + (\omega_0 - \omega)^2} | + | }{4} 2\text{Re} \left\{ \frac{1}{k^2 D+ i (\omega_0 - \omega )}\right\} \\ |
| + | &= \frac{ \left| x\right| ^2 | ||
| + | }{2} \frac{k^2D}{(k^2D)^2 + (\omega_0 - \omega)^2} | ||
\end{align}</math> | \end{align}</math> | ||
This is a Lorentzian curve, with a line width <math>\Delta\omega_\text{Dicke}= 2 | This is a Lorentzian curve, with a line width <math>\Delta\omega_\text{Dicke}= 2 | ||
| Line 1,028: | Line 1,051: | ||
\eta(\rho) = \frac{C_n^\prime a_n}{v \rho^{n-1}} | \eta(\rho) = \frac{C_n^\prime a_n}{v \rho^{n-1}} | ||
</math> | </math> | ||
| − | where <math>a_n = \int_{-\pi/2}^{\pi/2} \left| \sec\theta\right| ^{2-n}d\theta</math> is a | + | where <math>a_n = \int_{-\pi/2}^{\pi/2} \left| \sec\theta\right| |
| + | ^{2-n}d\theta</math> is a | ||
dimensionless constant of order unity. | dimensionless constant of order unity. | ||
Weisskopf's assumption was that for collisions with <math>\eta(\rho)\gtrsim 1</math> the | Weisskopf's assumption was that for collisions with <math>\eta(\rho)\gtrsim 1</math> the | ||
Revision as of 14:51, 5 February 2009
Contents
- 1 Resonance Line Shapes
- 1.1 Overview
- 1.2 Ideal Line Shape for Rabi Resonance
- 1.3 Line Shape for an Atomic Beam
- 1.4 Method of Separated Oscillatory Fields
- 1.5 Line Shape with Exponential Decay
- 1.6 Doppler and Recoil Shifts
- 1.7 Perturbation Theory of Spectral Broadening
- 1.8 Natural line width
- 1.9 Doppler broadening
- 1.10 Lineshape of Confined Particles
- 1.11 Fluorescent Spectrum of an Atom
- 1.12 Pressure Broadening
Resonance Line Shapes
In this chapter, we will discuss several phenomena which affect the line shape. Our motivation for this is simple: No resonance line is infinitely narrow. Unless we understand the line shape, we cannot extract spectroscopic information with high accuracy. For instance, the linewidth for an atomic fountain clock is typically Fourier limited (by the free-fall time of the atoms) to \unit{\sim1}{\hertz}. Reaching \unit{\sim10}{\micro\hertz} accuracy therefore requires splitting the line to a part in !
Overview
We begin with an incomplete list of mechanism that can modify the line shape: \begin{itemize}
* The interaction time of the atom with the probing field can be limited by
either intrinsic or technical factors, giving rise to a linewidth from simple Fourier broadening. In this category we can consider the natural linewidth due to the finite lifetime of the excited state, time-of-flight broadening due to the limited free-fall time of atoms in a fountain or flight time of atoms in a beam, and interaction time broadening due in general to atoms leaving the probing region. We will discuss these broadenings first when we consider the lineshapes and performance of the Rabi and Ramsey resonance methods below.
* There can be effects from the velocity of the atoms in the laboratory
frame, such as recoil shifts and Doppler broadening. These effects can be overcome by confining the particle; ideally to much less than a wavelength of the probing radiation, a situation known as the Lamb-Dicke regime.
* Collisions between atoms can both shift and broaden the line. They can
also, in some special cases, narrow it; a case known as Dicke narrowing.
* The power of the probing radiation can be high enough to cause the atom
to behave non-linearly, leading to saturation of the transition and power broadening of the resonance line. At high probe powers the nonlinear response of the atom can also give rise to additional peaks in the fluorescence spectrum, giving the so-called Mollow triplet.
* Externally applied fields can modify the energy of the levels involved in
the transition and thus shift the resonance. Inhomogeneities in these fields can also broaden the (observed) line by giving different atoms different resonance frequencies. \end{itemize} In general, we can distinguish between homogeneous broadening mechanisms, which widen the resonance line for each atom individually, and inhomogeneous broadening mechanisms, for which each atom's resonance remains narrow but acquires a randomly distributed frequency shift, so that the total response of an atomic ensemble is broadened. A simple guideline for distinguishing the two is that in the case of a homogeneously broadened line a single monochromatic probe laser can excite all the atoms in an ensemble equally, while for inhomogeneously broadened lines a monochromatic probe will excite some atoms strongly and others not at all. Homogeneous broadening is generally associated with random interruptions of the phase evolution of the atom, an exponential decay of the atomic coherences, and consequently a Lorentzian lineshape. Inhomogeneous broadening typically comes from random perturbations to the resonance frequency which, in the large-ensemble limit, follow a normal distribution, leading to a Gaussian lineshape. The distinction is not absolutely rigorous. For instance, collisional effects broaden an individual atom's response, but will be different for different atoms in an ensemble with different velocities. Also, while we have described shortening of the coherent interaction time as the special preserve of homogeneous broadening mechanisms, it turns out that all broadening mechanisms can be described by the decay of some suitably-defined correlation function after some characteristic time. This will form the basis for a very general and powerful formalism for discussing line shifts and broadening, which we will develop after first discussing some simple examples.
Ideal Line Shape for Rabi Resonance
The Rabi resonance transition probability,
has the following properties: \begin{itemize}
* It is {\it exact}, it is not a perturbative result.
* The amplitude of the oscillation of achieves a maximum value of 1 when
the resonance condition is satisfied: . At resonance is periodic in the product .
* As is increased, oscillates with increasing
frequency but decreasing amplitude. \end{itemize} If the interaction time is fixed and the power is varied at resonance, then achieves its maximum value when . Under these conditions the spin exactly "flips" under the influence of the applied field. If the frequency is then varied, varies as a function of as shown in Figure \ref{Rabi-curve} (a). The resonance curve has a full width at half maximum (FWHM) of , or, in units of Hz,
\begin{figure} \centering
\caption{Calculated lineshapes: Probabity of transition plotted as a function of . Curve a) single velocity: . Curve b) thermal atomic beam average; , where . Curve c) heavily saturated resonance, . From Reference \cite{Ramsey1956}.}
\end{figure}
Line Shape for an Atomic Beam
In practice the conditions described by the simple Rabi formula are rarely met exactly. In most cases, 2-level resonance involves averaging over some combination of interaction times, field strengths, and possibly resonance frequency. Figure \ref{Rabi-curve} (b) shows the situation for atomic beam resonance. In this case the experimental resonance curve depends on the distribution of interaction times due to the various speeds of atoms in the thermal atomic beam. In many cases the interaction time is not fixed, but is distributed according to a distribution of interaction times , where The observed quantity is the average transition probability which is given by
where . \begin{figure} \centering
\caption{Elementary atomic beam resonance experiment. a) source of atoms; b) collimation slit for atomic beam; A) and B) Stern-Gerlach magnets for deflecting atoms. These are inhomogeneous magnets which exert a force Magnet A, the "polarizer", selects a given value of ; magnet B, the "analyzer", allows the atoms to pass to the detector d only if remains unchanged. Resonance is induced in uniform field C) by the oscillating field from the coil ). At the resonance a transition occurs; the atom can no longer pass through the analyzer, and the signal to the detector d) falls. If the length of the coil is , then atoms moving with speed of interact with the oscillating field for time .}
\end{figure} In an atomic beam, for instance, the interaction time is , where is the speed. The distribution of speeds in an atomic beam can be found from the Maxwell-Boltzmann law and is
where is the most probable velocity of atoms of mass in a gas at temperature \footnote{Note that this is not the same as the distribution of speeds for a confined gas with isotropic velocity distribution, because atoms travelling at higher speeds have a higher probability of escaping the oven to join the beam.}\cite[p. 20]{Ramsey1956}. Thus, for a Maxwell- Boltzmann speed distribution the average transition probability is
where , and . The integral must be evaluated numerically (Tables are given in Appendix D of \cite{Ramsey1956}) Results are shown in Figure \ref{Rabi-curve} (b). has a maximum for . In contrast, in a monochromatic beam the maximum occurs for . The maximum transition probability is 0.75. The FWHM is
If we regard as the mean time for an atomic pass through the coil, then compared to the line width for a monoenergetic beam, Equation \ref{EQ_ideal2}, the effect of the velocity spread is to broaden the resonance curve by approximately two. Furthermore, all traces of periodic behavior have been erased.
Method of Separated Oscillatory Fields
The separated oscillatory field (SOF) technique is one of the most powerful methods of precision spectroscopy. As the name suggests, it involves two sequential applications of the transition-producing field to the system under study with an interval in between. This technique was originally conceived by Norman Ramsey in 1948 for application in RF studies of molecular beams using two separated resonance coils through which the molecular beams passed sequentially. It represents the first deliberate exploitation of a quantum superposition state. Subsequently it has been extended to high frequencies where the RF regions were in the radiation zone (i.e. source-free), to two photon transitions, to rapidly decaying systems, and to experiments where the two regions were temporally (rather than spatially) separated. It is routinely used to push measurements to the highest possible precision (eg. in the Cs beam time standard apparatus). Ramsey shared the 1990 Nobel prize for inventing this method. Figure \ref{Ramsey-apparatus} shows a typical configuration. \begin{figure} \centering
\caption{ Separated oscillatory field atomic beam resonance. The two-state atom experiences a pulse in the first oscillatory field, and another pulse in the second field. In between, the atom moves freely for distance L. As viewed in the rotating frame, on resonance the second field will have the correct phase on resonance, no matter how long it takes the atom to traverse distance L. Off-resonance, however, a phase difference accumulates with the increasing time. As a result, when the frequency is slowly swept, an interference pattern is generated whose frequency width is , where v is the atom's velocity. }
\end{figure} The atomic beam resonance region is composed of two oscillatory field regions, each of length , separated by distance . The resonance pattern reveals an interference fringe structure with characteristic width / , where is the most probable velocity for a thermal distribution of atoms at temperature (see the figure below). Of course a single Rabi coil of the same length would produce approximately the same resonance width. The transition probability for the Ramsey method can be calculated by straightforward application of the formalism presented earlier. Details are described in Reference \cite{Ramsey1956}, Section V.4.2. The result is that the transition probability for a two-state system is
where , and , where is the average energy separation of the two states along the path between the coil. and . The first line in this expression is just 4 times the probability of transition for a spin passing through one of the oscillating fields. All interference terms (which must involve ) are contained in the second term. The quantity is the phase difference accumulated by the spin in the field-free region relative to the oscillating field in the first region. If the phase in the second oscillating field region differs from the phase in the first region, the above results must be modified by adding the difference to in the above equations. \begin{figure} \centering
\caption{Transition probability by the separated oscillatory field method as a function of frequency. is the distance between the excitation regions; is the most probably velocity in the beam. Hence, is approximately the average time of the measuring process. The "Ramsey fringe" is shown by the solid line: it is superimposed on the "Rabi pedestal", dashed line, which is the resonance curve for a single oscillating field region. From Reference \cite{Ramsey1956}.}
\end{figure} The SOF technique is based on an interference between the excitations produced at two separated fields - thus it is sensitive to the phase difference (coherence) of the oscillating fields. The method is most easily understood by consideration of the classical spin undergoing magnetic resonance in SOF's. To maximize the interference between the two oscillating fields, we want there to be a probability of for a transition in each resonance region. This is achieved by adjusting both field intensities ( above) so that (an interaction with this property is termed a " pulse" if the system is at resonance, in which case the spin's orientation is now along in the rotating coordinate system). During the field-free time , the spin precesses merrily about the constant field between the two oscillating-field regions. When it encounters the second oscillatory field, it receives a second interaction equal to the first. If the system is {\it exactly} on resonance, this second interaction will just complete the inversion of the spin. If, on the other hand, the system is off resonance just enough so that (but ) then the spin will have precessed about an angle less far than the oscillating field. It will consequently lie in the - direction rather than in the direction in the coordinate system rotating with the second oscillatory field , and as a result the second field will precess the spin back to + , its original direction, and the probability of transition will be 0! A little more thought shows that the transition probability will oscillate sinusoidally with period . The central maximum of this interference pattern is centered at and its full width at half maximum (in -space) is . The central maximum can be made arbitrarily sharp simply by increasing . In fact, SOF can be used in this fashion to produce line widths for decaying particles which are narrower than the reciprocal of the natural line width! (This does not violate the uncertainty principle because SOF is a way of selecting only those few particles which have lived for time .) The separated oscillatory field method (the "Ramsey method") has the following important properties compared to the single field method ("Rabi method"). \begin{itemize}
* The resonance frequency depends on the {\it mean} energy
separation of the two states between the coils: instantaneous variations, for instance due to fluctuations in an applied field, either in space or in time, are averaged out.
* The Rabi method requires an applied oscillatory field having
uniform phase: this is difficult to accomplish if the flight path is long compared to the wavelength. In contrast, the Ramsey method requires only that the phase be constant across the short coils of length . As we will see, this means that Doppler effects can be to a large extent eliminated.
* By the Rabi method the resonance linewidth due to a thermal
beam is 1.07 , whereas by the Ramsey method it is only 0.65 The linewidth is reduced almost by a factor of two.
* In the presence of radiative decay or some other loss
mechanism the Ramsey method can be used to selectively observe long-lived atoms: atoms which have decayed are simply absent from the interference pattern. This makes it possible to observe a resonance line which is narrower than the "natural" linewidth, though one must pay a price in reduced signal intensity.
* Numerous experimental effects can be measured or reduced by
modulating the relative phase of the two fields.
* The method is not restricted to atomic beams: the important
point is that the applied fields interfere in {\it time}. The method can be applied to a fixed sample by applying the fields in some desired sequence of pulses.
* The field-free region (or the free-evolution time ) can be used to
enrich the experiment by having the atoms interact with some other system (such as a cavity, c.f. the work of the Haroche group) and observing the resulting phase change to the interference pattern. \end{itemize}
Line Shape with Exponential Decay
If the atoms decay by spontaneous emission, or are otherwise removed from the field by some sort of random process, then the distribution of interaction times is described by an exponential
The mean interaction time is . The average transition probability in a Rabi oscillation experiment is
has the familiar Lorentzian shape. The full
width at half maximum is
At low power, , and on resonance. As the power is increased, approaches a limiting value of 0.5, and the line starts to broaden. Broadening of a resonance line due to high power is called {\it saturation}. In the saturation regime the line width is ; \begin{figure} \centering
\caption{ Sketch of resonance line shape with exponential damping, for various values of the ratio . }
\end{figure} Note that we have assumed that all atoms decay out of the system with the same rate , irrespective of their internal state. If excited-state atoms decay out of the system at a different rate than ground-state ones, then we must replace by the average decay rate of the two levels. For instance, if excited atoms decay at while ground-state atoms are stable, we obtain
If, however, the excited state atoms decay back to the ground state, as is commonly the case, then the physics becomes considerably more subtle as the decayed atoms continue to participate in the oscillation (but with a random phase). For example, the 4 in the preceding equation becomes a 2. A correct treatment of saturation in this case requires the full optical Bloch equations.
Doppler and Recoil Shifts
In simple theoretical models, it is common to take the atomic mass , so that atomic motion is excluded from the problem. In this section we discuss the effects of the spatial motion of absorbing or emitting atoms of finite mass. We begin by considering an atom initially at rest and in the excited state. Before the atom spontaneously emits the total energy of the system is just the excited-state energy . After spontaneous emission it is . Here is the frequency of the emitted photon and is the momentum of the recoiling atom. From this we see that the frequency of the emitted photon is
For absorption a similar analysis gives the same result but with a sign. There is thus a small frequency difference, known as the recoil splitting, between the absorption and emission resonance frequencies for an atom at rest. The splitting is typically measured in \unit{}{\kilo\hertz}, and its observation by J.~Hall was one of the early triumphs of high-resolution laser spectroscopy. If we now consider an atom moving with speed Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} in a certain direction and which emits a photon in some direction which makes an angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} with its direction of motion, we see that the emitted photon's frequency is Doppler shifted in the lab frame to
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^\prime = \frac{\omega\left(1-\left(\frac{v}{c}\right)^2\right)^{1/2}} {1-\frac{v}{c}\cos\phi} }
Taylor-expanding this expression and combining it with the recoil term found above, we obtain
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \omega_{e,a}^\prime =\omega_{ba} \bigg[ & 1 \\ & + \frac{v}{c} \cos \phi \\ & - \left(\frac{v}{c}\right)^2 \left(\cos^2\phi + \frac{1}{2}\right) \\ & \mp \frac{\hbar\omega_{ba}}{2 M c^2}\bigg] \end{align}}
where the first line is the unshifted atomic frequency, the second gives the first-order Doppler shift, the third line gives the second-order relativistic Doppler shift (due to time dilation) and the last line gives the recoil shift. Of these, the first-order Doppler shift is typically the most important. It can, however, be eliminated in suitably crafted experimental configurations. The (usually much smaller) second-order Doppler term is unavoidable, since it comes from the relativistic time-dilation of the moving atom, and so it can dominate in certain precision experiments. For a typical gas, the Gaussian distribution of atomic velocities leads to a Gaussian frequency distribution:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(\omega) d\omega = \frac{1}{\sqrt{2 \pi}\omega_D} e^{-\left(\frac{\omega-\omega_0}{\omega_D}\right)^2}d\omega }
with a typical width Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_D = k \alpha} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = \sqrt{2 k_B T/ M}} is the most probable speed of the atoms in the gas. At room temperature this is usually of order \unit{}{\giga\hertz}, as compared to typical natural linewidths of \unit{\sim10}{\mega\hertz} and recoil shifts of a few to a few hundred \unit{}{\kilo\hertz}. In the general case, the Doppler broadened linewidth will have the form of a Voigt profile, the convolution of the Gaussian Doppler broadening with the Lorentzian natural lineshape. At room temperature this is well approximated by a Gaussian since the Doppler width is so much larger than the natural linewidth. However, even in this case, it is still possible to extract information about the underlying Lorentzian natural line by looking far out in the wings of the profile: because a Lorentzian decays so much more slowly than a Gaussian, it can be the dominant contribution to the lineshape at large detunings even when it is completely hidden in the Doppler broadening on resonance.
Perturbation Theory of Spectral Broadening
(Material in this section based in part on Section VIII-C of Reference \cite{Abragam1983}) We now consider a general formalism for spectral broadening, which covers the cases already discussed as well as many others. We shall consider a two-level system: the extension to a many level system is straightforward. The physical situation deals with a system which is initially in a given quantum state. The problem is to calculate the effect of a time-varying interaction. Instead of obtaining an exact solution, as we did when we obtained the Rabi oscillations, we will work within first order perturbation theory. The two-level system is described by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi = A u_a e^{-i\omega_a t} + B u_b e^{-i \omega_b t} }
The Hamiltonian is taken as , where the perturbation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is assumed to have no diagonal matrix elements. Schrodinger's equation gives
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\dot{A} &= \left\langle a\right| V (t) \left|b\right\rangle e^{-i\omega_0 t} B \\ i\dot{B} &= \left\langle b\right| V (t) \left|a\right\rangle e^{+i\omega_0 t} A \end{align}}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0 = \omega_b -\omega_a} . At Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = 0} the system is in state , so that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(0) = 1,} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(0) = 0} . If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{ba}} is the rate at which the system evolves from state
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|a\right\rangle}
to state , then
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{ba} = \frac{d \left| B(t)\right| ^2}{dt} = B^*\dot{B} + \dot{B}^* B = - iB^* \left\langle b\right| V(t) \left|a\right\rangle e^{+i\omega_0 t} A + \text{c.c.} }
Integrating Equation \ref{EQ_ptsb2} yields,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(t) = - i\int_0^t \left\langle b\right| V(t^\prime ) \left|a\right\rangle e^{+i\omega_0 t^\prime} A(t^\prime ) dt^\prime }
To first order, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(t^\prime ) = A(0) = 1} . Introducing this result in Equation \ref{EQ_ptsb3} gives
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{ba} = \int_0^t \left\langle a\right| V (t) \left|b\right\rangle \left\langle b\right| V(t^\prime ) \left|a\right\rangle e^{- i \omega_0 (t-t^\prime )} dt^\prime + c.c. }
It is convenient to introduce the correlation function
Usually, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ba}} does not depend explicitly on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t^\prime} , but only on their difference Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau = t^\prime - t} . In this case, Equation \ref{EQ_ptsb5} becomes
This formalism should give the same result as our earlier analysis in the limit of very short time, when first order perturbation theory should agree with an exact solution. Consider the case of a uniform oscillating field that generates a matrix element of the form
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle b\right| V(t) \left|a\right\rangle = \frac{x}{2} e^{-i\omega t} }
Then
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ba} (\tau ) = \frac{ \left| x\right| ^2}{4} e^{+i\omega \tau}, }
and
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{ba} = \frac{ \left| x\right| ^2}{4} \int_{-t}^{+t} e^{-i( \omega_0 -\omega ) \tau} d\tau = \frac{ \left| x\right| ^2}{2} \frac{\sin (\omega_0 - \omega ) t}{(\omega_0 - \omega )} }
In the limit of short time, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{ba}\rightarrow \left| x\right| ^2 t /2} . Compare this with the Rabi resonance formula derived earlier
In the limit , , and . With the identification , the results are the same. In many cases the perturbation varies from particle to particle, and our concern is to find the average response of the system. The results are the same in this case, but Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ba}} is now the ensemble-averaged correlation function. The correlation function provides a consistent way to analyze effects of motion or other decorrelating factors such as spectral fluctuations in the driving field. After some characteristic time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_c} called the correlation time, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ab}(\tau )\rightarrow 0} . Consequently, for times longer than Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_c} equation \ref{EQ_ptsb7} becomes
and the rate goes to a constant. This is the limit in which we recover rate equation behaviour and Fermi's Golden Rule. Note that the rate is given, in this limit, by frequency the component at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0} of the Fourier transform of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ba}(\tau)} . This is not surprising, as the Fourier transform of the correlation function is just the power spectrum of the time-dependent perturbation: the transition rate is proportional to the resonant part of that power spectrum. In this limit, we can approximately express the rate as
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{ba} \approx G_{ba}(0) \tau_c = \frac{1}{4}(\omega_R \tau_c)^2 / \tau_c }
This gives a qualitative picture of the connection between the short-time coherent evolution of the system and the long-time rate equation limit. The short-time behaviour is a quadratic increase of the population in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} , given by , as the amplitude transferred to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} adds coherently and interferes constructively. At long times the the population increases as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [(\omega_r \tau_c)^2 / 4] \times (t/\tau_c)} , with short coherent evolution steps of duration Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_c} adding incoherently and with random phase to give a linear population increase with time.
Natural line width
Excited atoms spontaneously decay to their ground state, except under very special circumstances. A proper treatment of spontaneous emission requires treating the field quantum mechanically. Nevertheless, we can include its effect here in a phenomenological fashion. The population of atoms in an excited state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} will decay in free space as
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_b = 1/\gamma_b} is called the natural lifetime of the state. We can introduce spontaneous decay into the state vector by writing it as
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi_b (t) = u_b e^{-i(\omega_b -i \gamma_b /2)t} }
i.e.\ by treating the energy as a complex quality. In this case, the population of atoms in state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} varies as
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(t) = N_0 \left| \Psi_b (t)\right| ^2 = N_0 e^{-\gamma_b t} }
as we surmised. Making this {\it ansatz}, the dipole matrix element due to an interaction with an oscillating field is
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = (\gamma_a +\gamma_b )} . (If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is the ground state of the system, then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_a = 0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma =\gamma_b } .) We have
From Equation \ref{EQ_cof3}, we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{ba} = \frac{ \left| x\right| ^2}{4} \int_{-\infty}^{\infty} e^{-\Gamma \left| \tau\right| /2} e^{-i(\omega_0 - \omega )\tau} d\tau = \frac{ \left| x\right| ^2}{2} \frac{ \frac{\Gamma}{2}}{{\left( \frac{\Gamma}{2} \right)^2} + {\left( \omega - \omega_0 \right)^2}} }
The result, not unexpected, is a Lorentzian line. Note, however, that the linewidth Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma} , does not depend on the power. In this first order treatment, saturation does not occur.
Doppler broadening
Consider a gas of atoms moving freely, irradiated by an electromagnetic plane wave
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{E}} = {\bf{\hat{\epsilon}}} E_0 e^{i ( kz + \omega t )} }
If the interaction is electric dipole, then
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle a\right| V \left|b\right\rangle = \frac{x}{2} e^{ikz} e^{i\omega t} }
where is the dipole matrix element. However, the situation here is quite general: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} can represent any form of interaction with the wave. The important factor is the phase associated with position, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ikz}} . If the atoms are moving, then
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ba} = \frac{ \left| x\right| ^2}{4} e^{i\omega (t^\prime-t)} \overline{e^{ik(z(t^\prime ) - z (t))}} }
Denoting the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} -component of an atom's velocity by , then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z (t^\prime) - z (t) = v \tau} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau = t^\prime - t} . We need to evaluate
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = \overline{e^{ikv\tau}} }
To take the system average, we use the well known Maxwell-Boltzmann distribution law for the velocity of an ideal gas particle
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(v_z ) = \frac{1}{\alpha \sqrt{\pi}} e^{-v_z^2 /\alpha^2} }
where is the most probable speed of the gas. (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} is the temperature, and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} is the atomic mass.) Taking the average in Equation \ref{EQ_db3} yields
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I= \frac{1}{\alpha \sqrt{\pi}} \int_{-\infty}^{\infty} e^{ikv\tau } e^{-v^2 /\alpha^2} dv }
The result is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = e^{-(k\alpha \tau )^2/4} }
so that
Equation \ref{EQ_cof3} becomes
The factor is the first order Doppler shift of an atom moving with the most probable speed . The spectral line shape has the form of a Gaussian with a width (FWHM)
i.e. the linewidth is just approximately twice the first order Doppler shift. Typically, for uncooled atoms. Note that here too we can think of the broadening as caused by an interruption in the coherent evolution of the atomic ensemble. The inverse of the most probable Doppler shift Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_c = 1/k\alpha = \mathchar'26\mkern-10mu\lambda / \alpha } is the characteristic decay time of the correlation function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ba}} . This is the time it takes for the random thermal motion of the atoms to spread them out over a wavelength of the radiation, so that they experience random phases of light. Another interpretation starts from the observation that the thermal atoms have a characteristic wavepacket size Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{DB} \sim \hbar / \Delta p \sim \hbar / m \alpha} . When the atom interacts with the probing field, the excited and ground-state components of the wavefunction actually have slightly different velocities, differing by the recoil velocity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar k / m} . The time is just the time it takes the excited and ground state components to move apart by the size of the wavepacket, at which point they become distinguishable and can no longer interfere to give coherent evolution. For an atom of mass 23 at a temperature of 500 K, absorbing radiation at 600 nm (sodium), the Doppler width is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \nu_D = \frac{1}{2\pi} \Delta \omega_D \unit{\sim 4}{GHz} }
Until the advent of lasers, Doppler broadening seriously limited the resolution of optical spectroscopy. In principle, it should also be a problem in microwave or radio-frequency spectroscopy since the fractional width, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \nu_D /\nu \sim \alpha /c \sim 10^{-5}} , is large compared to the resolution that can be achieved. However, as we shall demonstrate, it is essentially absent in laboratory experiments in those frequency regimes.
Lineshape of Confined Particles
Trapped particles offer the possibility of reaching the ultimate in spectroscopic precision: cooling the particle with lasers or electronics can reduce second order Doppler shifts at least to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-17}} (for 1 mK and atomic mass 10), proper design of the cavity can suppress spontaneous emission, and collisions can be virtually eliminated for single trapped particles in cryogenically pumped environments. The first order Doppler shift can be entirely eliminated also, in spite of the fact that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v/c} is not particularly small ( in the above example). Suppression of first order Doppler shift results from the spectrum of emission/absorption by a trapped particle---it consists of an unshifted central line with sidebands spaced apart by multiples of the frequency of oscillation. The amplitude of the sidebands may be reduced by lowering the amplitude of oscillation of the trapped particle, but it is also possible to address spectroscopically the unshifted central line---this approach underlies the Mossbauer effect as well as the use of buffer gases and specially coated containers to narrow spectra.
Spectrum of oscillating emitter
We now consider the lineshape (or equivalently the emission spectrum) of a harmonically bound particle. The absorption spectrum has the same shape, so we do not need to consider it separately. If the particle oscillates with amplitude Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} at frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_t} , then the phase of radiation emitted by the atom towards a detector situated at large Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} will contain the phase term
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi (t) = -kx(t) - \omega_0 t = - kx_0 \sin\omega_t t - \omega_0 t }
A wave with this phase will have an instantaneous frequency
consistent with the usual Doppler shift into the lab system, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{k} \cdot \vec{v}} . In the parlance of electrical enginering, signals with the above phase and frequency correspond to phase and frequency modulation, respectively. We shall find the spectrum from the phase since the amplitude of the phase oscillation is the physically important {\it modulation index}, which is just the maximum phase shift relative to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0 t} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = kx_0 = x_0/\lambdabar }
(This approach also avoids the common pitfall of assuming that the phase corresponding to frequency modulation is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega (t) t)} . Thus we must find the spectrum of a wave whose amplitude is proportional to
Some algebra using identities (See e.g.\ M. Abramowitz and I.A. Stegun 9.1.42)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos (z \sin \theta ) = J_0 (z) + 2 \sum_{k=1}^{\infty} J_{2k} (z) \cos (2k\theta ) }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin (z \sin \theta ) = 2 \sum_{k=0}^{\infty} J_{2k+1} (z) \sin [(2k+1)\theta ] }
gives
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a (t) = \sum_{n = -\infty}^{\infty} (-1)^n J_{n} (\beta ) \cos [(\omega_0 + n \omega_t )t] }
Obviously the system does not have a continuous lineshape, rather the emission is either at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0} or sidebands which differ from by a multiple of the trapping frequency, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\omega_t} . (Physically this results from the exactly periodic nature of the motion.) The probability of emission at frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0 + n \omega_t} is simply Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{n}^2 (\beta )} , hence the intensity spectrum of the emitted light is proportional to
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I (\omega )\propto \sum_{n=-\infty}^{\infty} J_n^2 (\beta ) \delta ( \omega - \omega_0 - n \omega_t ) }
An alternative and intuitively appealing derivation of these results is to consider the quantum number of the bound oscillating particle explicitly in the calculation. Then the initial state is an atom in state trapped in quantum state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i} of the trap; after emission the atom is in state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} in quantum state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_f} of the trap. The frequency of the emitted photon determined from energy conservation,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega = \hbar \omega_{ba} - E_i^\text{trap} - E_f^\text{trap} }
in general, and
for harmonic motion, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n= n_i - n_f} . This expression needs no correction for recoil since the initial and final kinetic energies of the atom are explicitly accounted for in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_i^\text{trap}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_f^\text{trap}} . The transition rate is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R \propto |{ \left\langle \psi_f^\text{trap}\right| e^{-i {\bf{k}} \cdot {\bf{r}} } \left|\psi_i^\text{trap}\right\rangle }|^2 }
If the matrix element is evaluated in the momentum representation is a translation operator (by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\hbar {\bf{k}} } ) so this factor becomes Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\braket{\phi_f( {\bf{p}} - \hbar {\bf{k}} )}{\phi_i( {\bf{p}} }}}|^2} . In the case of a harmonic oscillator with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i , n_f \gg 1} , the confinement factor will yield the Bessel function expression consistent with Equation \ref{EQ_soe6}. The preceding view bears much similarity to electronic transitions in molecular spectroscopy in that an electronic transition occurs between two states with quantized vibrational motion. Indeed, the matrix element involving the trap states in Equation \ref{EQ_soe8} is analogous to the Frank-Condon factor in molecular spectroscopy (except Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ik r} \approx 1} owing to the small size of molecules) This association emphasizes the generality of Equation \ref{EQ_soe8}: it applies equally to non-harmonic traps, and even to traps (as for neutral atoms) in which the confinement potential differs for states and .
Weak confinement, classical regime
Consider the case in which the particle is weakly confined so that the amplitude of oscillation is many wavelengths. In this case the maximum phase shift is large and the spectrum will contain many sidebands. We refer to this as the classical regime because the quantization of frequencies in the spectrum may be neglected while attention is concentrated on the overall lineshape. The viewpoint is completely justified for weak traps in which the trapping frequency is less than the spontaneous linewidth---then the sidebands are too close to be resolved and the spectrum will be continuous.
Tight confinement
The most dramatic effects associated with tightly confined radiators occur when the particles are confined to dimensions smaller than one wavelength of the emitted light (tight confinement, also known as the Lamb-Dicke regime). This is evident from the confinement matrix element in Equation \ref{EQ_soe8}: if the spatial extent of the wavefunctions associated with is , then and it is reasonable to expand Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-i {\bf{k}} \cdot {\bf{r}} }\approx 1 - i {\bf{k}} \cdot {\bf{r}} } . The first term will give the selection rule Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = f} (since the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_i} are orthonormal) and hence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = \omega_{ba}} exactly. The second term will give rise to sidebands, but with matrix elements of order these will be weak.
Recoilless emission
Emission with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = f} is called recoilless emission because the atom has the same momentum distribution after the emission as before. The momentum of the photon is provided (or taken up in the case of absorption) by the trap itself. This is analogous to the Mossbauer effect in which the momentum is taken up by the crystal as a whole. There the confinement matrix element with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = i} is called the {\it Debye-Waller} factor.
Whither the Doppler shift?
It may seem surprising that confined particles, which often have very large velocities as they oscillate in the trapping potential, can nonetheless be completely free of Doppler broadening. The key point is that it is not the instantaneous value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\bf{k}} \cdot {\bf{v}} } which sets the correlation time and hence the line broadening, but rather the time required for different atoms in the ensemble to accumulate phases that differ by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi} . In a trap, though is large, its sign changes regularly as the atom oscillates, the phase excursions in each direction cancel exactly, and so the accumulated phase remains small. Even though they are moving rapidly at any given time, tightly confined atoms continue to see the same phase of the driving light and never decorrelate. Note that for experiments in the radio and microwave frequency regimes, the long wavelength of the radiation (sometimes longer than the size of the experiment!) makes the tight-confinement condition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0/\lambda \ll 1} very easy to satisfy, so that (first-order) Doppler broadening is hardly ever a problem.
Trapping and Dicke narrowing
The concept of the confined particle can be generalized: It is not necessary to confine particles harmonically in order to achieve significant narrowing. In 1953 Dicke pointed out \cite{Dicke1953} that collisions could reduce the usual Doppler width substantially if two conditions were met: the mean free path must be much smaller than the wavelength, and the collisions must not destroy the coherence between the radiating states. The essence of Dicke's argument was that gas collisions could be viewed as a succession of traps each with a different frequency (he considered traps with steep walls rather than harmonic springs, but this is immaterial). All particles would have a recoilless line at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = \omega_{ba}} , and the average over the traps with different frequencies would average the other lines into a broad spectrum with approximately the original Doppler width. We can estimate the lineshape in the case of Dicke narrowing as follows: consider an atom moving diffusively through an inert buffer gas, so that collisions do not disturb the coherence between ground and excited state. For an atom moving diffusively, the probability of being at position Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^\prime} , assuming that at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = 0} it was at , is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(z^\prime , z, t) = \frac{1}{\sqrt{4\pi D \left| t\right| }} e^{-(z^\prime - z)^2/4 D \left| t\right| } }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} is the diffusion constant. Writing Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^\prime - z = s} we need to evaluate
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ba} = \frac{ \left| x\right| ^2 }{4} \overline{ e^{-iks}} e^{i\omega\tau} = \frac{ \left| x\right| ^2 }{4} \frac{e^{i \omega\tau}}{\sqrt{4\pi D \left| \tau\right| }} \int_{-\infty}^{\infty} e^{-s^2/4 D \left| \tau\right| } e^{-iks} ds = \frac{ \left| x\right| ^2 }{4} e^{-k^2D \left| \tau\right| } e^{i\omega\tau} }
Then
This is a Lorentzian curve, with a line width Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\omega_\text{Dicke}= 2 k^2 D} . For an ideal gas, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = \overline{v} \ell /3} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell} is the mean free path and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{v}} is the average speed. Taking , and writing Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = 2\pi /\lambda = 1 / \mathchar'26\mkern-10mu\lambda } , we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \omega_\text{Dicke} = \frac{2}{3} k\alpha \frac{\ell}{ \mathchar'26\mkern-10mu\lambda } \sim \Delta \omega_D \times \frac{\ell}{ \mathchar'26\mkern-10mu\lambda } }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\omega_D} is the Doppler line width. As the mean free path Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell } is made short compared to the wavelength, the Doppler broadening vanishes. Note that our description included only the long-time diffusive motion of the atoms. If we had also included the ballistic motion for times less than the mean collision time, we would also have recovered the broad Doppler pedestal that is observed in experiments.
Fluorescent Spectrum of an Atom
So far we have mostly been discussing the absorption spectrum of atoms, i.e. the response of the atom as a function of the frequency of the drive laser. However, it can also be interesting to consider the spectrum of the scattered light for a fixed drive frequency, known as the fluorescence spectrum. Consider the case of an infinitely heavy atom at rest (thus neglecting recoil and Doppler effects) illuminated by monochromatic radiation of some fixed detuning , at very low power (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_R \ll \Gamma} ). In this situation the scattered light is also monochromatic and has exactly the same frequency as the drive; not the resonance frequency of the atom, unless the drive happens to be on resonance. From a classical perspective, this is because the weakly driven atom behaves as a linear oscillator, and the steady-state response of a linear oscillator is always at the drive frequency. From a quantum-mechanical perspective we can say that in the weak drive limit photons are scattered one at a time; since energy must be conserved in every complete scattering event, the scattered photon must have the same energy and frequency as the incident ones. For a strong, near-resonant drive, the situation becomes more complicated as the saturated atom's response is no longer linear. Classically, the scattered radiation is now modulated by (generalized) Rabi oscillations. Quantum-mechanically, the multi-photon processes that become possible at high drive intensities need only conserve energy in total. It is therefore possible to scatter a photon at lower frequency than the drive, provided that there is another photon simultaneously scattered at a higher frequency than the drive. This leads to a characteristic pair of sidebands in the fluorescent spectrum, symmetrical about the component at the drive frequency; a structure known as the Mollow triplet. It is best analyzed in the dressed atom formalism, and is discussed in some detail in 8.422.
Pressure Broadening
Up to this point we have assumed that the atom's internal state is unaffected by the presence of other atoms around it. This situation can be realized almost exactly in some experiments, such as those involving single trapped ions, but usually collisions or interactions between atoms in a sample act to shift and broaden atomic resonances. Depending on context and the theoretical framework used to discuss them, these effects are referred to as mean-field effects, clock shifts, collision shifts, or pressure broadening. While a full discussion of these phenomena is beyond the scope of 8.421, we will present a few simple models to introduce some of the relevant physics.
Impact Approximation: Lorentz Model (1906)
If we consider the excited atom as an oscillator, we can ask how its oscillation is affected by a collision with another atom. A simple first guess is that, just like a spontaneous emission event, the collision stops the oscillation by resetting the atom to its ground state. The drive field then restarts the oscillation (after a time on the order of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_R^{-1}} ) which persists until it is quenched by another collision (after some mean collision time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} ) or until the atom decays by spontaneous emission. A more plausible model for neutral atom collisions, which are typically elastic, is that the oscillation is not interrupted by the collision but that its phase jumps randomly. Our model is then of continuous oscillation with sudden phase discontinuities occurring on average every collision time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} . Both models give the same result, namely that the pressure-broadened line remains Lorentzian but is broadened by the increased decoherence rate. With random interruptions to coherent evolution occurring on average every collision time , the FWHM of the Lorentzian is increased to
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_\text{total} = \Gamma_\text{natural} + \frac{1}{\tau} = \Gamma_\text{natural} + a P }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} is the pressure and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is a constant relating the pressure to the characteristic time for dephasing from collisions and hence to the line broadening. The important assumption made in both these descriptions is that the collision time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_c \rightarrow 0} . In other words, we are ignoring the collisions' dynamics and treating them as instantaneous interruptions to the coherent evolution of the atom. This assumption is known as the impact approximation. In order to assess its validity we must first consider in more detail how an inter-atomic collision can affect the internal state of the atom. When two atoms are a finite distance apart, the eigenstates of the system are not the free-atom energy eigenstates we found at the beginning of the course, but rather the molecular eigenstates of the two nuclei and all their electrons treated as a whole. If we treat the inter-atomic distance as a parameter (Born-Oppenheimer approximation), then these molecular levels will map back onto the free-atom energy levels as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\rightarrow\infty} (i.e. in the limit of weak interatomic interaction). For finite Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} , we can consider the molecular potentials Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_g(r)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_e(r)} , the deviations of the molecular eigenenergies from the free-state ground- and excited-state energies onto which they map. In terms of these, the instantaneous rate of phase change is given by the difference of the ground and excited state molecular potentials.
Our model of a collision (within the impact approximation) is then of a very brief period where the atoms come close enough that the instantaneous frequency is substantially modified. After the collision the atoms return to their normal oscillation frequency, but with a phase that has been modified by an amount
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{\tau_c} \dot{\phi} dt = \int_{\tau_c} \frac{1}{\hbar}[V_e(r(t))-V_g(r(t))] dt }
Given the sensitivity of to the exact collision energy and impact parameter, the phase change is essentially random. Given that we know the transition frequency as a function of inter-atomic separation, we might also try to find the pressure-broadened spectrum from the distribution of inter-atomic separation:
where is the probability that two atoms are at a distance which produces a frequency shift . The simplest pair correlation function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(r)} would be
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(r)dr = \frac{4\pi r^2}{V} dr }
with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=n^{-1}} the average volume per atom. This model gives obviously different predictions from the previous one. For instance, the spectrum can now be asymmetric or have complicated structure, depending on the exact shape of the molecular potential curves as captured in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\omega(r)} . Which model is correct? One useful guideline comes from Fourier theory. A frequency shift can only be resolved if it is larger than the inverse of the collision time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\omega > \tau_c^{-1}} . For small Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\omega} , near the resonance, the details of the molecular potential are not resolvable in the spectrum and the impact approximation can be expected to give reasonable results; the region of the spectrum within Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sim1/\tau_c} will still resemble a (broadened) Lorentzian. At large Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\omega} , far out in the wings of the resonance, the molecular potentials can appreciably modify the spectrum. Thus, studies of far-detuned light scattering can be useful for probing the molecular potentials and testing models of the inter-atomic interaction.
Beyond the Impact Approximation: Weisskopf Theory (1933)
We have not yet specified how to find , the mean time between collisions that appears as an additional broadening in the Lorentz model. Weisskopf theory attempts to do so, by giving a quantitative criterion for distinguishing "hard" collisions that scramble the phase and decohere the atom as in the Lorentz model from "soft" collisions that merely shift the phase a little and lead to line shifts. The starting assumption is that the atomic dipole continues to oscillate throughout the collision, but that its phase is modified by the interatomic potential as we have just discussed. In particular, the total phase change Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} is given by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta = \int_{-\infty}^{\infty} \Delta\omega dt }
It will turn out that the relevant collisions will be very long range, for which the inter-atomic forces are weak so that a collision essentially consists of one atom flying by the other in a straight line. Also, at long ranges, molecular potentials (such as van der Waals potential) are typically well-approximated by inverse power of the inter-atomic distance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} . We therefore write
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Delta\omega &= \frac{C_n^\prime}{r^n} \\ r &= \rho + v t \\ \eta(\rho) &= \int_{-\infty}^\infty \frac{C_n^\prime dt}{(\rho^2 + v^2 t^2)^{n/2}} \end{align}}
Here is a constant characterizing the difference between the molecular potentials in the ground and excited states, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} is the impact parameter, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} is the speed of one atom relative to the other, and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} is the time measured from the moment of closest approach. By making the substitution Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v t = \rho \tan\theta} we can carry out the integral and find that
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n = \int_{-\pi/2}^{\pi/2} \left| \sec\theta\right| ^{2-n}d\theta} is a dimensionless constant of order unity. Weisskopf's assumption was that for collisions with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta(\rho)\gtrsim 1} the phase is disrupted and the coherence is lost. This leads to the definition of a Weisskopf radius
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_W \equiv \left(\frac{C_n^\prime a_n}{\overline{v}}\right)^{1/n-1} }
which is the maximum impact parameter for a decohering collision with the ensemble average relative speed . The rate of decohering collisions used in the Lorentz model is then
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\tau} = \pi \rho_W^2 n \overline{v} }
with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} the atomic number density. Weisskopf theory successfully explains the fact that the cross sections required to explain pressure broadening (\unit{\sim10^{-14}..10^{-15}}{\centi\metre\squared}) are much larger than the usual gas kinetic cross sections for momentum redistribution between atoms (\unit{\sim10^{-16}{\centi\metre\squared}}). It does not, however, treat the effect of soft (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta<1} ) phase-changing collisions at all, and so accounts only for pressure broadening, not pressure shifts.
Including Pressure Shifts: Lindholm Theory (1941)
We have already seen in Section \ref{SEC_PTSB} that the line shape can be expressed as the Fourier transform of a suitable correlation function of the phase. Given that we know how to calculate the phase change due to a collision (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta(\rho)} ), we can calculate this correlation function by taking an ensemble average over random impact parameters. The details are worked out in Demtroder's Laser Spectroscopy text (c.f. excerpts posted on the course webpage). As expected, long-range collisions (, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta\ll 1} ) do not contribute appreciably to the line broadening but do shift the line frequency, while short-range collisions (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho<\rho_W} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta\gtrsim 1} ) do not contribute to the line shift but broaden the resonance.
Some Numbers
For the sodium D line in an argon buffer gas,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \text{Broadening:} & \unit{30}{\mega\hertz\per\text{torr}} \\ \text{Shift:} & \unit{-1}{\mega\hertz\per\text{torr}} \\ \text{Self-broadening:} & \unit{150}{\mega\hertz\per\text{torr}} \end{align}}
Here the broadening and shift are given as a function of the buffer gas pressure (Na-Ar collisions), while the self-broadening is given for the sodium gas pressure (Na-Na collisions). Note that even at pressures of several torr these effects can be small relative to the room-temperature Doppler width of \unit{\sim1-2}{\giga\hertz}. \putbib




















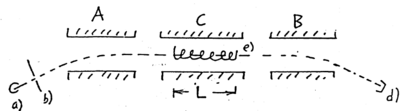




















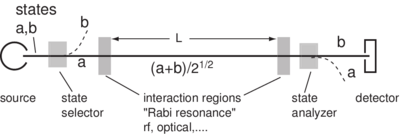





![{\displaystyle {\begin{aligned}P=&4{\frac {\omega _{R}^{2}}{a^{2}}}\sin ^{2}(a\tau /2)\times \\&\left[\cos(\delta \omega T/2)\cos(a\tau /2)-\left({\frac {\omega -\omega _{0}}{a}}\right)\sin(\delta \omega T/2)\sin(a\tau /2)\right]^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe3e7fe74f504a7338854ea99646ab0d2b3af05a)






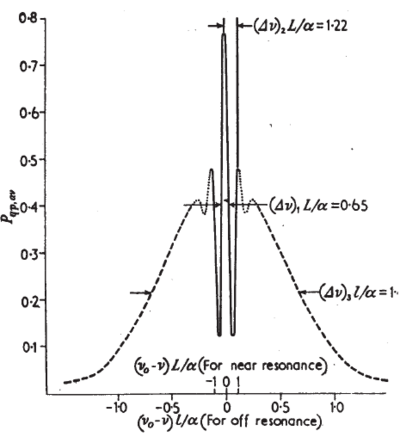























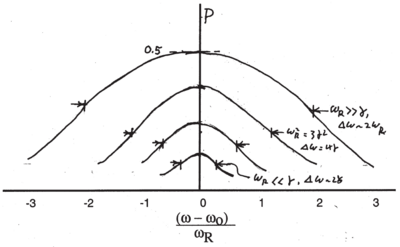




















































![{\displaystyle {\dot {\phi }}=\Delta \omega ={\frac {1}{\hbar }}[V_{e}(r)-V_{g}(r)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/549ccb97ed1f86183e79e65d9488d8f3c7355fff)







