Difference between revisions of "Fine Structure and Lamb Shift"
imported>Ketterle |
imported>Ketterle |
||
| Line 1: | Line 1: | ||
=== Introduction === | === Introduction === | ||
| + | |||
| + | <categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;" hideprefix=auto>8.421</categorytree> | ||
| + | |||
Immediately adjacent to Michelson and Morley's announcement of | Immediately adjacent to Michelson and Morley's announcement of | ||
their failure to find the ether in | their failure to find the ether in | ||
| Line 12: | Line 15: | ||
using the old quantum theory, as it was later christened, accounted | using the old quantum theory, as it was later christened, accounted | ||
precisely for the splitting. | precisely for the splitting. | ||
| − | |||
| − | |||
Sommerfeld's theory gave the lie to Einstein's dictum "The Good | Sommerfeld's theory gave the lie to Einstein's dictum "The Good | ||
Revision as of 04:25, 24 February 2010
Contents
Introduction
Immediately adjacent to Michelson and Morley's announcement of their failure to find the ether in an 1887 issue of the Philosophical Journal is a paper by the same authors reporting that the H line of hydrogen is actually a doublet, with a separation of 0.33 cm. In 1915 Bohr suggested that this "fine structure" of hydrogen is a relativistic effect arising from the variation of mass with velocity. Sommerfeld, in 1916, solved the relativistic Kepler problem and using the old quantum theory, as it was later christened, accounted precisely for the splitting.
Sommerfeld's theory gave the lie to Einstein's dictum "The Good Lord is subtle but not malicious", for it gave the right results for the wrong reason: his theory made no provision for electron spin, an essential feature of fine structure. Today, all that is left from Sommerfeld's theory is the fine structure constant . The theory for the fine structure in hydrogen was provided by Dirac whose relativistic electron theory (1926) was applied to hydrogen by Darwin and Gordon in 1928. They found the following expression for the energy of an electron bound to a proton of infinite mass:
where is the principal quantum number, , and . The Dirac equation is not nearly as illuminating as the Pauli equation, which is the approximation to the Dirac equation to the lowest order in v/c.
The first term is the electron's rest energy; the following two terms are the non relativistic Hamiltonian, and the last term, the fine structure interaction, is given by
The relativistic contributions can be described as the {\it kinetic, spin-orbit,} and {\it Darwin} terms, , , and , respectively. Each has a straightforward physical interpretation.
Kinetic contribution
Relativistically, the total electron energy is E = . The kinetic energy is
Thus
Spin-Orbit Interaction
According to the Dirac theory the electron has intrinsic angular momentum and a magnetic moment . The electron g-factor, . As the electron moves through the electric field of the proton it "sees" a motional magnetic field
where . However, there is another contribution to the effective magnetic field arising from the Thomas precession. The relativistic transformation of a vector between two moving co- ordinate systems which are moving with different velocities involve not only a dilation, but also a rotation (cf Jackson, {\it Classical Electrodynamics}). The rate of rotation, the Thomas precession, is
Note that the precession vanishes for co-linear acceleration. However, for a vector fixed in a co-ordinate system moving around a circle, as in the case of the spin vector of the electron as it circles the proton, Thomas precession occurs. From the point of view of an observer fixed to the nucleus, the precession of the electron is identical to the effect of a magnetic field.
Substituting , and into Eq.\ \ref{EQ_soitwo} gives
Hence the total effective magnetic field is
This gives rise to a total spin-orbit interaction
The Darwin Term
Electrons exhibit "Zitterbewegung", fluctuations in position on the order of the Compton wavelength, . As a result, the effective Coulombic potential is not , but some suitable average , where the average is over the characteristic distance . To evaluate this, expand about in terms of a displacement ,
Assume that the fluctuations are isotropic. Then the time average of is
The precise expression for the Darwin term is
The coefficient of the Darwin term is 1/8, rather than 1/6. Recall that , so that the Darwin term is nonzero only for states, where . That is, the Zitterbewegung effectively cuts off the cusp of the potential, thereby reducing the binding energy for -electrons.
Evaluation of the fine structure interaction
\begin{figure}
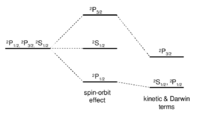
(caption: Fine structure of levels in hydrogen. The degeneracy between the and levels, which looks accidental in non-relativistic quantum mechanics, is really deeply rooted in the relativistic nature of the system. The degeneracy is ultimatly broken in QED by the Lamb Shift.)
\end{figure} The spin orbit-interaction is not diagonal in or {\bf S} due to the term . However, it is diagonal in . and are likewise diagonal in . Hence, finding the energy level structure due to the fine structure interaction involves evaluating . Note that vanishes in an state, and that vanishes in all states but an state. It is left as an exercise to show that
Note that states of a given and are degenerate. This degeneracy is a crucial feature of the Dirac theory.
The Lamb Shift
According to the Dirac theory, states of the hydrogen atom with the same values of and are degenerate. Hence, in a given term, (), (), (), etc. form degenerate doublets. However, as described in Chapter 1, this is not exactly the case. Because of vacuum interactions, not taken into account, in the Dirac theory, the degeneracy is broken. The largest effect is in the state. The energy splitting between the and states is called the Lamb Shift. A simple physical model due to Welton and Weisskopf demonstrate its origin. In the following derivation, note the analogy between the vacuum fluctuations inducing the Lamb Shift and the Zitterbewegung responsible for the Darwin term treated in section \ref{SEC_dt}. Because of zero point fluctuation in the vacuum, empty space is not truly empty. The electromagnetic modes of free space behave like harmonic oscillators, each with zero-point energy . The density of modes per unit frequency interval and per volume is given by the well known expression
Consequently, the zero-point energy density is
With this energy we can associate a spectral density of radiation
The bar denotes a time average and and are the field amplitudes. Hence,
For the moment we shall treat the electron as if it were free. Its motion is given by
The effect of the fluctuation is to cause a change in the average potential
can be found by a Taylor's expansion:
When we average this in time, the second term vanishes because {\bf s} averages to zero. For the same reason, in the final term, only contributions with remain. We have, taking the average,
Since we obtain finally
Since , we obtain the following expression for the change in energy
The matrix element gives contributions only for states, where its value is
Combining Eqs.\ \ref{EQ_lambsix}, \ref{EQ_lambtweleve} into Eq.\ \ref{EQ_lambeleven} yields
Integrating over some yet to be specified frequency limits, we obtain
At this point, atomic units come in handy. Converting by the usual prescription, we obtain
The question remaining is how to choose the cut-off frequencies for the integration. It is reasonable that is approximately the frequency of an orbiting electron, in atomic units. At lower energies, the electron could not respond. For the upper limit, a plausible guess is the rest energy of the electron, . Hence, . For the state, this gives
- atomic~units MHz
The actual value is 1,058 MHz. Measurements of the Lamb shift \cite{Lamb1947, Weitz1994, Schwob1999} have occupied the forefront of hydrogen spectroscopy from Lamb's original 1947 discovery, using microwave techniques, of a shift of "about 1000 Mc/sec" to more recent results at the level of precision obtained in the optical domain by two-photon spectroscopy.



![{\displaystyle {\frac {E}{mc^{2}}}={\left[{\frac {1}{\sqrt {\frac {\alpha Z}{n-k+{\sqrt {k^{2}-\alpha ^{2}Z^{2}}}}}}}\right]^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b03decb353205d3f96fa4b7d5d1c6a760ee73f)









![{\displaystyle T=E-mc^{2}=(mc^{2}){\left[{\sqrt {1+{\frac {p^{2}}{m^{2}c^{2}}}}}-1~~\right]}={\frac {p^{2}}{2m}}-{\frac {1}{8}}{\frac {p^{4}}{m^{3}c^{2}}}+\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc695e8be75e63a5d72e966b6e14fd7eeb899702)




















![{\displaystyle \Delta V\sim {\frac {1}{2}}{\left[{\frac {1}{3}}{\left({\frac {\hbar }{mc}}\right)^{2}}\right]}\nabla ^{2}V=-{\frac {1}{6}}{\frac {e^{2}\hbar ^{2}}{m^{2}c^{2}}}\nabla ^{2}\left({\frac {1}{r}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90dd5f34606adfcb4dbc1b8d5ca7df80561feedb)