Interferometer shot noise limit

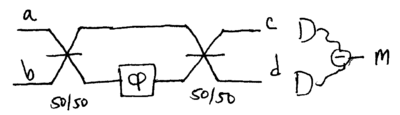
The Poisson distribution of photon number in coherent (laser) light contributes an uncertainty of $\Delta n\sim {\sqrt {n}}$ to optical measurements. It is therefore reasonable to anticipate that with $n$ photons, the uncertainty $\Delta \phi$ with which an unknown phase $\phi$ can be determined might be bounded below by $\Delta \phi \geq 1/{\sqrt {n}}$, based on the heuristic that $\Delta n\Delta \phi \geq 1$. Such a limit is known as being due to shot noise, arising from the particle nature of photons, as we shall now see rigorously. Consider a Mach-Zehnder interferometer constructed from two 50/50 beamsplitters, used to measure $\phi$:

Let us analyze this interferometer, first by using a traditional quantum optics approach in the Heisenberg picture, and second by using single photons in the Schrodinger picture.

Sensitivity limit for Mach-Zehnder interferometer

Previously, we've defined the unitary transform for a quantum beamsplitter as being a rotation about the ${\hat {y}}$ axis, so as to avoid having to keep track of factors of $i$. For variety, let's now use a different definition; nothing essential will change. Let the 50/50 beamsplitter transformation be

$B={\frac {1}{\sqrt {2}}}\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\,.$

This acts on $[a,b]^{T}$ to produce operators describing the output of the beamsplitter; in particular,

$\left[{\begin{array}{c}{a-ib}\\{b-ia}\end{array}}\right]=B\left[{\begin{array}{c}{a}\\{b}\end{array}}\right]\,.$

Similarly, the phase shifter acting on the mode operators performs

$P=\left[{\begin{array}{cc}{1}&{0}\\{0}&{e^{i\phi }}\end{array}}\right]\,.$

The Mach-Zehnder transform is thus

${\begin{array}{rcl}U&=&BPB\\&=&{\frac {1}{2}}\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\left[{\begin{array}{cc}{1}&{0}\\{0}&{e^{i\phi }}\end{array}}\right]\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\\&=&-ie^{i\phi /2}\left[{\begin{array}{cc}{\sin(\phi /2)}&{\cos(\phi /2)}\\{\cos(\phi /2)}&{-\sin(\phi /2)}\end{array}}\right]\,.\end{array}}$

The way we have defined these transformations here, the output modes of the interferometer, $c$ and $d$, are

$\left[{\begin{array}{c}{c}\\{d}\end{array}}\right]=U\left[{\begin{array}{c}{a}\\{b}\end{array}}\right]\,.$

We are interested in the difference between the photon numbers measured at the two outputs, $M=(d^{\dagger }d-c^{\dagger }c)/2$, where the extra factor of two is introduced for convenience. We find

${\begin{array}{rcl}c^{\dagger }c&=&\sin ^{2}{\frac {\phi }{2}}a^{\dagger }a+\cos ^{2}{\frac {\phi }{2}}b^{\dagger }b+\sin {\frac {\phi }{2}}(a^{\dagger }b+b^{\dagger }a)\\d^{\dagger }d&=&\cos ^{2}{\frac {\phi }{2}}a^{\dagger }a+\sin ^{2}{\frac {\phi }{2}}b^{\dagger }b-\sin {\frac {\phi }{2}}(a^{\dagger }b+b^{\dagger }a)\end{array}}$

The measurement result $M$ is thus

$M=(a^{\dagger }a-b^{\dagger }b)\cos \phi -(a^{\dagger }b+b^{\dagger }a)\sin \phi \,.$

Define $X=a^{\dagger }a-b^{\dagger }b$, and $Y=a^{\dagger }b+b^{\dagger }a$. Recognizing that $X$ is the difference in photon number between the two output arms, and recalling that this is the main observable result from changing $\phi$, we identify the signal we wish to see as being $X$.

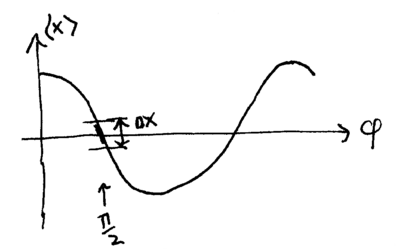
Ideally, the output signal should go as $\cos \phi$. The signal due to $Y$ goes as $\sin \phi$, and we shall see that this is the noise on the signal. The average output signal $\langle X{\rangle }$, as a function of $\phi$, looks like this:

Note that if our goal is to maximize measurement sensitivity to changes in $\phi$, then the best point to operate the interferometer at is around $\phi =\pi /2$, since the slope $d\langle x{\rangle }/d\phi$ is largest there. At this operating point, if the interferometer's inputs have laser light coming into only one port, then the outputs have equal intensity; thus, the interferometer is sometimes said to be "balanced" when $\phi =\pi /2$.

What is the uncertainty in our measurement of $\phi$, derived from the observable $M$? By propagating uncertainties, this is

${\langle }\Delta \phi ^{2}\rangle ={\frac {{\langle }\Delta M^{2}{\rangle }}{\left|{\frac {\partial \langle M{\rangle }}{\partial \phi }}\right|^{2}}}\,,$

where

${\frac {\partial \langle M{\rangle }}{\partial \phi }}=-X\sin \phi -Y\cos \phi \,.$

Let $\phi =\pi /2$, such that $M=Y$, and $\partial M/\partial \phi =-X$.

Limit for coherent state input

For a coherent state input, $|\psi _{in}\rangle =|\alpha {\rangle }|0{\rangle }$, we find

${\begin{array}{rcl}\langle X\rangle &=&\langle 0|{\langle }\alpha |(a^{\dagger }a-b^{\dagger }b)|\alpha {\rangle }|0{\rangle }\\&=&|\alpha |^{2}\\&=&n\,,\end{array}}$

if we define $n=|\alpha |^{2}$ as the input state mean photon number. Also,

${\begin{array}{rcl}\langle Y\rangle =\langle 0|{\langle }\alpha |(a^{\dagger }b+b^{\dagger }a)|\alpha {\rangle }|0\rangle =0\,.\end{array}}$

This is consitent with our intuition: the signal should go as $\sim n$, and the undesired term goes as $Y$, so it is good that is small on average. However, there are nontrivial fluctuations in $Y$, because

$\langle Y^{2}\rangle =\langle a^{\dagger }ba^{\dagger }b+a^{\dagger }bb^{\dagger }a+b^{\dagger }ab^{\dagger }a+b^{\dagger }aa^{\dagger }b{\rangle }\,,$

and $\langle a^{\dagger }bb^{\dagger }a\rangle =\langle a^{\dagger }a(1+b^{\dagger }b){\rangle }$ is nonzero for the coherent state! Specifically, the noise in $Y$ is

$\langle Y^{2}\rangle =|\alpha |^{2}=n\,,$

and thus the variance in the measurement result is

${\langle }\Delta M^{2}\rangle =\langle Y^{2}\rangle -\langle Y{\rangle }^{2}=|\alpha |^{2}=n\,.$

From Eq.(\ref{eq:l7-dphi}), it follows that the uncertainty in $\phi$ is therefore

${\langle }\Delta \phi \rangle ={\frac {\sqrt {{\langle }\Delta M^{2}{\rangle }}}{\left|{\frac {\partial \langle M{\rangle }}{\partial \phi }}\right|}}={\frac {\sqrt {n}}{n}}={\frac {1}{\sqrt {n}}}\,.$

This is a very reasonable result; as the number of photons used increases, the accuracy with which $\phi$ can be determined increases with ${\sqrt {n}}$. The improvement arises because greater laser power allows better distinction between the signals in $c$ and $d$.

Limit for single photons

Another way to arrive at the same result, using single photons, gives an alternate interpretation and different insight into the physics.

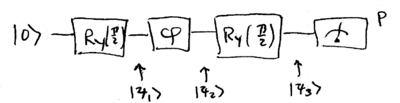
As we have seen previously, acting on the $|01{\rangle }$, $|10{\rangle }$ "dual-rail" photon state, a 50/50 beamsplitter performs a $R_{y}(\pi /2)$ rotation, and a phase shifter performs a $R_{z}(\phi )$ rotation. The Mach-Zehnder interferometer we're using can thus be expressed as this transform on a single qubit:

where the probability of measuring a single photon at the output is $P$. Walking through this optical circuit, the states are found to be

${\begin{array}{rcl}|\psi _{1}\rangle &=&{\frac {|0{\rangle }+|1{\rangle }}{\sqrt {2}}}\\|\psi _{2}\rangle &=&{\frac {|0{\rangle }+e^{i\phi }|1{\rangle }}{\sqrt {2}}}\\|\psi _{3}\rangle &=&{\frac {1-e^{i\phi }}{2}}|0\rangle +{\frac {1+e^{i\phi }}{2}}|1{\rangle }\,,\end{array}}$

such that

$P={\frac {1+\cos \phi }{2}}\,.$

Repeating this $n$ times (so that we use the same average number of photons as in the coherent state case), we find that the standard deviation in $P$ is

$\Delta P={\sqrt {\frac {p(1-p)}{n}}}={\frac {\sin \phi }{2{\sqrt {n}}}}\,.$

Given this, the uncertainty in $\phi$ is

$\Delta \phi ={\frac {\Delta \phi }{\left|{\frac {dP}{d\phi }}\right|}}={\frac {1}{\sqrt {n}}}\,.$

This is the same uncertainty as we obtained for the coherent state input, but the physical origin is different. Now, we see the noise as being due to statistical fluctuations of a Bernoulli point process, one event at a time. The ${\sqrt {n}}$ noise thus comes from the amount of time the signal is integrated over (assuming a constant rate of photons). The noise is simply shot noise.