Squeezed light interferometry

Heisenberg-limited interferometry can also be accomplished using a variety of states of light, including squeezed states we studied in Section~2.2. Let us explore three configurations here. Vacuum squeezed state input. Because squeezed states can move noise between the $x$ and $p$ quadratures, it is intuitively reasonable that a state with low phase noise could be used to provide more accurate measurements of $\phi$ than is possible with a coherent state, which has equal noise in the two quadratures.

It might seem counter-intuitive, however, that we can get to the Heisenberg limit by replacing not the coherent state input, but rather, the vacuum state, in the Mach-Zehnder interferometer. This works because at the balanced operating point, the noise in the output is due to fluctuations entering in at the vacuum port. Before, we used $|\alpha {\rangle }|0{\rangle }$ as input. Let us now replace this by

$|\psi _{in}=|\alpha \rangle |0_{r}{\rangle }\,,$

where $|0_{r}\rangle =S(r)|0{\rangle }$ is a squeezed vacuum state. Recall that for the balanced interferometer, the final uncertainty in the phase measurement is

${\langle }\Delta \phi \rangle ={\frac {\sqrt {{\langle }\Delta Y^{2}{\rangle }}}{|\langle X{\rangle }|}}\,,$

where $X=a^{\dagger }a-b^{\dagger }b$, and $Y=a^{\dagger }b+b^{\dagger }a$. For the squeezed vacuum + coherent state input, we find

${\begin{array}{rcl}\langle X\rangle &=&{\langle }\alpha |a^{\dagger }a|\alpha \rangle -\langle 0_{r}|b^{\dagger }b|0_{r}\rangle \approx |\alpha |^{2}=n\\\langle Y\rangle &\approx &0\\\langle Y^{2}\rangle &\approx &|\alpha ^{2}|\langle 0_{r}|(b+b^{\dagger })^{2}|0_{r}{\rangle }=|\alpha ^{2}|e^{-r}\,.\end{array}}$

Thus, the uncertainty in the phase measurement is approximately

${\langle }\Delta \phi \rangle \approx {\frac {e^{-r/2}}{\sqrt {n}}}\,.$

In the limit of large squeezing, ie $r\rightarrow \infty$, the squeezed vacuum has nonzero average photon number, $\langle 0_{r}|b^{\dagger }b|0_{r}\rangle \sim \sinh ^{2}r=n_{b}$, so this expression does not vanish to zero. Rather, there is an optimal amount of squeezing, at which point the minimum phase uncertainty goes as ${\langle }\Delta \phi _{min}\rangle \sim 1/(n+n_{b})$, which is close to the Heisenberg limit. See Caves, {\em Quantum-mechanical noise in an interferometer,} Phys. Rev. D, vol~23, p.~1693, 1981, for more on this subject.

Yurke state input.

The Heisenberg limit can also be reached using the Mach-Zehnder interferometer by replacing the input light states with this unusual squeezed state

$|\psi _{in}\rangle ={\frac {1}{\sqrt {2}}}\left[{|n-1{\rangle }|n\rangle +|n{\rangle }|n-1\rangle }\right]\,.$

This is known as the Yurke state. It happens to be balanced already, and thus instead of operating our interferometer at $\phi =\pi /2$, we operate it at $\phi =0$, such that the output measurement gives $M=X$, and $\partial M/\partial \phi =Y$, and the final uncertainty in the phase measurement is

${\langle }\Delta \phi \rangle ={\frac {\sqrt {{\langle }\Delta X^{2}{\rangle }}}{|\langle Y{\rangle }|}}\,.$

For the Yurke state,

${\begin{array}{rcl}(a^{\dagger }b+b^{\dagger }a)|n-1,n\rangle &=&{\sqrt {n}}{\sqrt {n}}|n{\rangle }|n-1{\rangle }+{\sqrt {n-1}}{\sqrt {n+1}}|n-2{\rangle }|n+1{\rangle }\\(a^{\dagger }b+b^{\dagger }a)|n,n-1\rangle &=&n|n-1{\rangle }|n{\rangle }+{\sqrt {(n-1)(n+1)}}|n+1{\rangle }|n-2{\rangle }\,.\end{array}}$

In calculating $\langle Y{\rangle }$, the terms with $|n-2{\rangle }$ drop out, leaving us with

$\langle Y\rangle ={\frac {\langle n,n-1|Y|n-1,n\rangle +\langle n-1,n|Y|n,n-1{\rangle }}{2}}=n\,.$

Similarly, it is straightforward to show that

${\begin{array}{rcl}\langle X\rangle &=&0\\\langle X^{2}\rangle &=&\langle n_{a}^{2}-2n_{a}n_{b}+n_{b}^{2}\rangle =2\,.\end{array}}$

Thus, the uncertainty in $\phi$ is

${\langle }\Delta \phi \rangle ={\frac {\sqrt {2}}{n}}\,,$

which is (up to a factor of two) the Heisenberg limit.

Yurke state: Experiment?

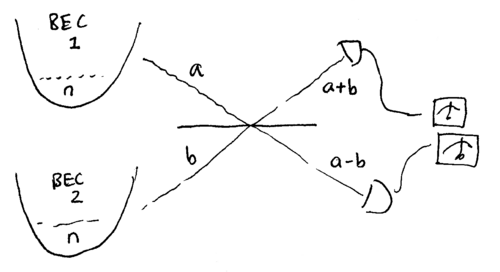
Given how useful the Yurke state could be for interferometry, it is meaningful to consider how such a state might be made. One interesting proposal starts with two Bose-Einstien condenstates, prepared in a state of definite atom number, which we may model as two number eigenstates $|n{\rangle }|n{\rangle }$. The two condensates are weakly linked through a tunnel, which we may model as a beamsplitter, and detectors are placed to look for a single atom at the outputs. This is sketched below:

If the top detector clicks, then one atom has left the condensates; however, it is unknown from which it came. The post-measurement state, after this single click, is thus

${\begin{array}{rcl}|\psi \rangle &=&{\frac {a+b}{\sqrt {2}}}|n{\rangle }|n{\rangle }\\&=&{\sqrt {n}}|n-1{\rangle }|n\rangle +{\sqrt {n}}|n{\rangle }|n-1{\rangle }\,,\end{array}}$

written unnormalized. Normalized, the proper post-measurement state is

$|\psi \rangle ={\frac {|n-1{\rangle }|n\rangle +{\sqrt {n}}|n{\rangle }|n-1{\rangle }}{\sqrt {2}}}\,.$

This is the Yurke state. If the bottom detector had clicked instead, we would have obtained $|n-1{\rangle }|n{\rangle }-|n{\rangle }|n-1{\rangle }$ instead, which is also useful.

Similar techniques, involving beamsplitter mixed detection of spontaneous emission, can be used to entangle atoms (as we shall see later). More about this BEC entanglement method can be found in the literature; see, for example, Castin & Dalibard, Phys. Rev. A vol.~55, p.~4330, 1997, for the proposal to create Yurke states; Vogels, Chin, and Ketterle, Phys. Rev. Lett., vol.~90, p.~030403, 2003, for an experiment in which a squeezed BEC state was generated, and Bouyer and Kasevitch, Phys. Rev. A, vol.~56, p.~R1083, 1997, for a proposal to do Heisenberg limited spectroscopy with BECs.