imported>Ichuang |
imported>Ichuang |
| Line 301: |
Line 301: |
| | which meets the Heisenberg limit. | | which meets the Heisenberg limit. |
| | === Squeezed light interferometry === | | === Squeezed light interferometry === |
| − | Heisenberg-limited interferometry can also be accomplished using a
| + | |
| − | variety of states of light, including squeezed states we studied in
| + | {{#lst:Squeezed light interferometry|content}} |
| − | Section~2.2. Let us explore three configurations here.
| + | |
| − | Vacuum squeezed state input. Because squeezed states can move
| |
| − | noise between the <math>x</math> and <math>p</math> quadratures, it is intuitively
| |
| − | reasonable that a state with low phase noise could be used to provide
| |
| − | more accurate measurements of <math>\phi</math> than is possible with a coherent
| |
| − | state, which has equal noise in the two quadratures.
| |
| − | It might seem counter-intuitive, however, that we can get to the
| |
| − | Heisenberg limit by replacing not the coherent state input, but
| |
| − | rather, the vacuum state, in the Mach-Zehnder interferometer. This
| |
| − | works because at the balanced operating point, the noise in the output
| |
| − | is due to fluctuations entering in at the vacuum port. Before, we
| |
| − | used <math>|\alpha{\rangle}|0{\rangle}</math> as input. Let us now replace this by
| |
| − | :<math> | |
| − | |\psi_{in} = |\alpha \rangle |0_r{\rangle}
| |
| − | \,,
| |
| − | </math>
| |
| − | where <math>|0_r \rangle = S(r)|0{\rangle}</math> is a squeezed vacuum state. Recall that for
| |
| − | the balanced interferometer, the final uncertainty in the phase
| |
| − | measurement is
| |
| − | :<math>
| |
| − | {\langle}\Delta\phi \rangle = \frac{\sqrt{{\langle}\Delta Y^2{\rangle}}}{| \langle X{\rangle}|}
| |
| − | \,,
| |
| − | </math>
| |
| − | where <math>X = a^\dagger a - b^\dagger b </math>, and <math>Y = a^\dagger b+ b^\dagger a</math>. For the squeezed
| |
| − | vacuum + coherent state input, we find
| |
| − | :<math>\begin{array}{rcl}
| |
| − | \langle X \rangle &=& {\langle}\alpha| a^\dagger a |\alpha \rangle - \langle 0_r| b^\dagger b |0_r \rangle \approx
| |
| − | |\alpha|^2 = n
| |
| − | \\
| |
| − | \langle Y \rangle &\approx& 0
| |
| − | \\
| |
| − | \langle Y^2 \rangle &\approx& |\alpha^2| \langle 0_r|(b+ b^\dagger )^2|0_r{\rangle}
| |
| − | = |\alpha^2| e^{-r}
| |
| − | \,.
| |
| − | \end{array}</math>
| |
| − | Thus, the uncertainty in the phase measurement is approximately
| |
| − | :<math>
| |
| − | {\langle}\Delta\phi \rangle \approx \frac{e^{-r/2}}{\sqrt{n}}
| |
| − | \,.
| |
| − | </math>
| |
| − | In the limit of large squeezing, ie <math>r\rightarrow\infty</math>, the squeezed
| |
| − | vacuum has nonzero average photon number, <math> \langle 0_r| b^\dagger b |0_r \rangle \sim
| |
| − | \sinh^2 r = n_b</math>, so this expression does not vanish to zero. Rather, there
| |
| − | is an optimal amount of squeezing, at which point the minimum phase
| |
| − | uncertainty goes as <math>{\langle}\Delta\phi_{min} \rangle \sim 1/(n+n_b)</math>, which is
| |
| − | close to the Heisenberg limit. See Caves, {\em Quantum-mechanical
| |
| − | noise in an interferometer,} Phys. Rev. D, vol~23, p.~1693, 1981, for
| |
| − | more on this subject.
| |
| − | Yurke state input. The Heisenberg limit can also be reached
| |
| − | using the Mach-Zehnder interferometer by replacing the input light
| |
| − | states with this unusual squeezed state
| |
| − | :<math>
| |
| − | |\psi_{in} \rangle = \frac{1}{\sqrt{2}} \left[ { |n-1{\rangle}|n \rangle +
| |
| − | |n{\rangle}|n-1 \rangle } \right]
| |
| − | \,.
| |
| − | </math>
| |
| − | This is known as the Yurke state. It happens to be balanced
| |
| − | already, and thus instead of operating our interferometer at
| |
| − | <math>\phi=\pi/2</math>, we operate it at <math>\phi=0</math>, such that the output
| |
| − | measurement gives <math>M=X</math>, and <math>\partial M/\partial \phi= Y</math>, and the
| |
| − | final uncertainty in the phase measurement is
| |
| − | :<math>
| |
| − | {\langle}\Delta\phi \rangle = \frac{\sqrt{{\langle}\Delta X^2{\rangle}}}{| \langle Y{\rangle}|}
| |
| − | \,.
| |
| − | </math>
| |
| − | For the Yurke state,
| |
| − | :<math>\begin{array}{rcl}
| |
| − | ( a^\dagger b + b^\dagger a) |n-1,n \rangle &=& \sqrt{n} \sqrt{n} |n{\rangle}|n-1{\rangle}
| |
| − | + \sqrt{n-1}\sqrt{n+1} |n-2{\rangle}|n+1{\rangle}
| |
| − | \\
| |
| − | ( a^\dagger b + b^\dagger a) |n,n-1 \rangle &=& n |n-1{\rangle}|n{\rangle}
| |
| − | + \sqrt{(n-1)(n+1)} |n+1{\rangle}|n-2{\rangle}
| |
| − | \,.
| |
| − | \end{array}</math>
| |
| − | In calculating <math> \langle Y{\rangle}</math>, the terms with <math>|n-2{\rangle}</math> drop out, leaving us with
| |
| − | :<math>\begin{array}{rcl}
| |
| − | \langle Y \rangle = \frac{ \langle n,n-1|Y|n-1,n \rangle + \langle n-1,n|Y|n,n-1{\rangle}}{2} = n
| |
| − | \,.
| |
| − | \end{array}</math>
| |
| − | Similarly, it is straightforward to show that
| |
| − | :<math>\begin{array}{rcl}
| |
| − | \langle X \rangle &=& 0
| |
| − | \\
| |
| − | \langle X^2 \rangle &=& \langle n_a^2 - 2n_an_b + n_b^2 \rangle = 2
| |
| − | \,.
| |
| − | \end{array}</math>
| |
| − | Thus, the uncertainty in <math>\phi</math> is
| |
| − | :<math>
| |
| − | {\langle}\Delta\phi \rangle = \frac{\sqrt{2}}{n}
| |
| − | \,,
| |
| − | </math>
| |
| − | which is (up to a factor of two) the Heisenber limit.
| |
| − | Given how useful the Yurke state could be for interferometry, it is
| |
| − | meaningful to consider how such a state might be made. One
| |
| − | interesting proposal starts with two Bose-Einstien condenstates,
| |
| − | prepared in a state of definite atom number, which we may model as two
| |
| − | number eigenstates <math>|n{\rangle}|n{\rangle}</math>. The two condensates are weakly linked
| |
| − | through a tunnel, which we may model as a beamsplitter, and detectors
| |
| − | are placed to look for a single atom at the outputs. This is sketched
| |
| − | below:
| |
| − | ::[[Image:chapter2-quantum-light-part-5-interferometry-l7-yurke-state-bec.png|thumb|408px|none|]]
| |
| − | If the top detector clicks, then one atom has left the condensates;
| |
| − | however, it is unknown from which it came. The post-measurement
| |
| − | state, after this single click, is thus
| |
| − | :<math>\begin{array}{rcl}
| |
| − | |\psi \rangle &=& \frac{a+b}{\sqrt{2}} |n{\rangle}|n{\rangle}
| |
| − | \\
| |
| − | &=& \sqrt{n} |n-1{\rangle}|n \rangle + \sqrt{n}|n{\rangle}|n-1{\rangle}
| |
| − | \,,
| |
| − | \end{array}</math>
| |
| − | written unnormalized. Normalized, the proper post-measurement state
| |
| − | is
| |
| − | :<math>
| |
| − | |\psi \rangle = \frac{|n-1{\rangle}|n \rangle + \sqrt{n}|n{\rangle}|n-1{\rangle}}{\sqrt{2}}
| |
| − | \,.
| |
| − | </math>
| |
| − | This is the Yurke state. If the bottom detector had clicked instead,
| |
| − | we would have obtained <math>|n-1{\rangle}|n{\rangle}-|n{\rangle}|n-1{\rangle}</math> instead, which is also
| |
| − | useful. Similar techniques, involving beamsplitter mixed detection of
| |
| − | spontaneous emission, can be used to entangle atoms (as we shall see
| |
| − | later). More about this BEC entanglement method can be found in the
| |
| − | literature; see, for example, Castin & Dalibard, Phys. Rev. A
| |
| − | vol.~55, p.~4330, 1997, for the proposal to create Yurke states;
| |
| − | Vogels, Chin, and Ketterle, Phys. Rev. Lett., vol.~90, p.~030403, 2003,
| |
| − | for an experiment in which a squeezed BEC state was generated, and
| |
| − | Bouyer and Kasevitch, Phys. Rev. A, vol.~56, p.~R1083, 1997, for a
| |
| − | proposal to do Heisenberg limited spectroscopy with BECs.
| |
| | === Sensitivity to loss === | | === Sensitivity to loss === |
| | Entangled states, while very useful for a wide variety of tasks, | | Entangled states, while very useful for a wide variety of tasks, |
Quantum states and dynamics of photons
Interferometry and metrology
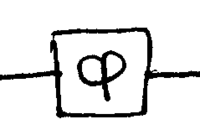
Suppose you are given a phase shifter of unknown  :
:
\noindent
How accurately can you determine  , given a certain time, and
laser power?
In this section, we consider this basic measurement problem, and show
how the usual shot noise limit can be exceeded by using quantum states
of light, reaching a quantum limit determined by Heisenberg's
uncertainty principle. This limit is achieved using entanglement,
which can be realized using entangled multi-mode photons, or by a
variety of squeezed states. The physics behind such quantum
measurement techniques generalizes to a wide range of metrology
problems, but a common challenge the need to reduce loss.
, given a certain time, and
laser power?
In this section, we consider this basic measurement problem, and show
how the usual shot noise limit can be exceeded by using quantum states
of light, reaching a quantum limit determined by Heisenberg's
uncertainty principle. This limit is achieved using entanglement,
which can be realized using entangled multi-mode photons, or by a
variety of squeezed states. The physics behind such quantum
measurement techniques generalizes to a wide range of metrology
problems, but a common challenge the need to reduce loss.
Shot noise limit
The Poisson distribution of photon number in coherent (laser) light
contributes an uncertainty of  to optical
measurements. It is therefore reasonable to anticipate that with
to optical
measurements. It is therefore reasonable to anticipate that with  photons, the uncertainty
photons, the uncertainty  with which an unknown phase
with which an unknown phase
 can be determined might be bounded below by
can be determined might be bounded below by  , based on the heuristic that
, based on the heuristic that  . Such a limit is known as being due to shot noise, arising
from the particle nature of photons, as we shall now see rigorously.
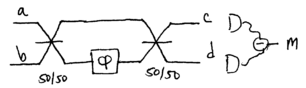
Consider a Mach-Zehnder interferometer constructed from two 50/50
beamsplitters, used to measure
. Such a limit is known as being due to shot noise, arising
from the particle nature of photons, as we shall now see rigorously.
Consider a Mach-Zehnder interferometer constructed from two 50/50
beamsplitters, used to measure  :
:
\noindent
Let us analyze this interferometer, first by using a traditional
quantum optics approach in the Heisenberg picture, and second by using
single photons in the Schrodinger picture.
Previously, we've defined the unitary transform for a quantum
beamsplitter as being a rotation about the  axis, so as to
avoid having to keep track of factors of
axis, so as to
avoid having to keep track of factors of  . For variety, let's now
use a different definition; nothing essential will change.
Let the 50/50 beamsplitter transformation be
. For variety, let's now
use a different definition; nothing essential will change.
Let the 50/50 beamsplitter transformation be
![{\displaystyle B={\frac {1}{\sqrt {2}}}\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e2d43ef535ef4f670f31b7ce4cfe7a15c1890f8)
This acts on ![{\displaystyle [a,b]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcbe0f3bd3d712a823544cc4985e4dbd35b6967d) to produce operators describing the output of
the beamsplitter; in particular,
to produce operators describing the output of
the beamsplitter; in particular,
![{\displaystyle \left[{\begin{array}{c}{a-ib}\\{b-ia}\end{array}}\right]=B\left[{\begin{array}{c}{a}\\{b}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74285e68d424d09733069d48c00a49acc738cec9)
Similarly, the phase shifter acting on the mode operators performs
![{\displaystyle P=\left[{\begin{array}{cc}{1}&{0}\\{0}&{e^{i\phi }}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f0a39e65796a1cc92d0a2ea729186ca5aca7a58)
The Mach-Zehnder transform is thus
![{\displaystyle {\begin{array}{rcl}U&=&BPB\\&=&{\frac {1}{2}}\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\left[{\begin{array}{cc}{1}&{0}\\{0}&{e^{i\phi }}\end{array}}\right]\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\\&=&-ie^{i\phi /2}\left[{\begin{array}{cc}{\sin(\phi /2)}&{\cos(\phi /2)}\\{\cos(\phi /2)}&{-\sin(\phi /2)}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aff63aa7808a03191a5315b3f548834ce336f41)
The way we have defined these transformations here, the output modes
of the interferometer,  and
and  , are
, are
![{\displaystyle \left[{\begin{array}{c}{c}\\{d}\end{array}}\right]=U\left[{\begin{array}{c}{a}\\{b}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9786a4cebe3997ae8ab2e2a99556bd27a67b002)
We are interested in the difference between the photon numbers
measured at the two outputs,  , where the
extra factor of two is introduced for convenience. We find
, where the
extra factor of two is introduced for convenience. We find

The measurement result  is thus
is thus

Define  , and
, and  . Recognizing that
. Recognizing that
 is the difference in photon number between the two output arms,
and recalling that this is the main observable result from changing
is the difference in photon number between the two output arms,
and recalling that this is the main observable result from changing
 , we identify the signal we wish to see as being
, we identify the signal we wish to see as being  . Ideally,
the output signal should go as
. Ideally,
the output signal should go as  . The signal due to
. The signal due to  goes
as
goes
as  , and we shall see that this is the noise on the signal.
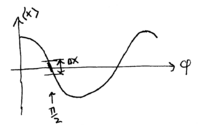
The average output signal
, and we shall see that this is the noise on the signal.
The average output signal  , as a function of
, as a function of  , looks like this:
, looks like this:
\noindent
Note that if our goal is to maximize measurement sensitivity to
changes in  , then the best point to operate the interferometer
at is around
, then the best point to operate the interferometer
at is around  , since the slope
, since the slope  is largest
there. At this operating point, if the interferometer's inputs have
laser light coming into only one port, then the outputs have equal
intensity; thus, the interferometer is sometimes said to be
"balanced" when
is largest
there. At this operating point, if the interferometer's inputs have
laser light coming into only one port, then the outputs have equal
intensity; thus, the interferometer is sometimes said to be
"balanced" when  .
What is the uncertainty in our measurement of
.
What is the uncertainty in our measurement of  , derived from the
observable
, derived from the
observable  ? By propagating uncertainties, this is
? By propagating uncertainties, this is

where

Let  , such that
, such that  , and
, and  .
For a coherent state input,
.
For a coherent state input,  , we find
, we find

if we define  as the input state mean photon number.
Also,
as the input state mean photon number.
Also,

This is consitent with our intuition: the signal should go as  , and the undesired term goes as
, and the undesired term goes as  , so it is good that is small on
average. However, there are nontrivial fluctuations in
, so it is good that is small on
average. However, there are nontrivial fluctuations in  , because
, because

and  is nonzero for the
coherent state! Specifically, the noise in
is nonzero for the
coherent state! Specifically, the noise in  is
is

and thus the variance in the measurement result is

From Eq.(\ref{eq:l7-dphi}), it follows that the uncertainty in  is therefore
is therefore

This is a very reasonable result; as the number of photons used
increases, the accuracy with which  can be determined increases
with
can be determined increases
with  . The improvement arises because greater laser power
allows better distinction between the signals in
. The improvement arises because greater laser power
allows better distinction between the signals in  and
and  .
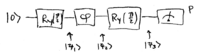
Another way to arrive at the same result, using single photons, gives
an alternate interpretation and different insight into the physics.
As we have seen previously, acting on the
.
Another way to arrive at the same result, using single photons, gives
an alternate interpretation and different insight into the physics.
As we have seen previously, acting on the  ,
,  "dual-rail" photon state, a 50/50 beamsplitter performs a
"dual-rail" photon state, a 50/50 beamsplitter performs a
 rotation, and a phase shifter performs a
rotation, and a phase shifter performs a  rotation. The Mach-Zehnder interferometer we're using can thus be
expressed as this transform on a single qubit:
rotation. The Mach-Zehnder interferometer we're using can thus be
expressed as this transform on a single qubit:
\noindent
where the probability of measuring a single photon at the output is
 . Walking through this optical circuit, the states are found to be
. Walking through this optical circuit, the states are found to be

such that

Repeating this  times (so that we use the same average number of
photons as in the coherent state case), we find that the standard
deviation in
times (so that we use the same average number of
photons as in the coherent state case), we find that the standard
deviation in  is
is

Given this, the uncertainty in  is
is

This is the same uncertainty as we obtained for the coherent state
input, but the physical origin is different. Now, we see the noise as
being due to statistical fluctuations of a Bernoulli point process,
one event at a time. The  noise thus comes from the amount
of time the signal is integrated over (assuming a constant rate of
photons). The noise is simply shot noise.
noise thus comes from the amount
of time the signal is integrated over (assuming a constant rate of
photons). The noise is simply shot noise.
Heisenberg limit: entanglement
The shot noise limit we have just seen, however, is not fundamental.
Here is a simple argument that something better should be possible.
Recall that the desired signal at the output of our Mach-Zehnder
interferometer is  , and the noise is
, and the noise is  .
If the inputs have
.
If the inputs have  and
and  , and if
, and if  were zero, then
the measured signal would be
were zero, then
the measured signal would be  . And at the balanced
operating point
. And at the balanced
operating point  ,
,

Thus, if the smallest photon number change resolvable is  ,
then
,
then  , from which it follows that
, from which it follows that

This is known as the "Heisenberg limit" on interferometry. There
are some general proofs in the literature that such a limit is the
best possible on interferometry. It governs more than just
measurements of phase shifters; gyroscopes, mass measurements, and
displacement measurements all use interferometers, and obey a
Heisenberg limit.
The argument above only outlines a sketch for why  might be an
achievable limt, versus
might be an
achievable limt, versus  ; it assumes that the noise
; it assumes that the noise  can be made zero, however, and does not provide a means for
accomplishing this in practice.
Many ways to reach the Heisenberg limit in interferometry are now
known. Given the basic structure of a Mach-Zehnder interferometer,
can be made zero, however, and does not provide a means for
accomplishing this in practice.
Many ways to reach the Heisenberg limit in interferometry are now
known. Given the basic structure of a Mach-Zehnder interferometer,
\noindent
one can consider changing the input state  , changing the
beamsplitters, or changing the measurement.
Common to all of these approaches is the use of entangled states. How
entanglement makes Heisenber-limited interferometry possible can be
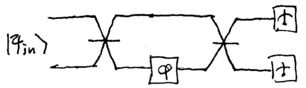
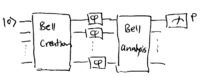
demonstrated by the following setup. Let us replace the beamsplitters
in the Mach-Zehnder interferometer with entangling and dis-entangling
devices:
, changing the
beamsplitters, or changing the measurement.
Common to all of these approaches is the use of entangled states. How
entanglement makes Heisenber-limited interferometry possible can be
demonstrated by the following setup. Let us replace the beamsplitters
in the Mach-Zehnder interferometer with entangling and dis-entangling
devices:
\noindent
Conceptually, the unusual beamsplitters may be the nonlinear
Mach-Zehnder interferometers we discussed in Section~2.3. They may
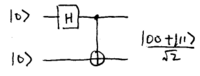
also be described by simple quantum circuits, using the Hadamard and
controlled-{\sc not} gate; for two qubits, the circuit is
\noindent
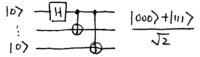
Note how the output is one of the Bell states. For three qubits, the
circuit is
\noindent
This output state,  (suppressing normalization) is
known as a GHZ (Greenberger-Horne-Zeilinger) state. Straightforward
generalization leads to larger "Schrodinger cat" states
(suppressing normalization) is
known as a GHZ (Greenberger-Horne-Zeilinger) state. Straightforward
generalization leads to larger "Schrodinger cat" states
 , using one Hadamard gate and
, using one Hadamard gate and  controlled-{\sc not} gates. Note that the reversed circuit
unentangles the cat states to produce computational basis states.
The important feature of such
controlled-{\sc not} gates. Note that the reversed circuit
unentangles the cat states to produce computational basis states.
The important feature of such  -qubit cat states, for our purpose,
is how they are transformed by phase shifters. A single qubit
-qubit cat states, for our purpose,
is how they are transformed by phase shifters. A single qubit
 becomes
becomes  . Similarly, two entangled
qubits in the state
. Similarly, two entangled
qubits in the state  , when sent through two phase
shifters, becomes
, when sent through two phase
shifters, becomes  , since the phases add. And
, since the phases add. And
 qubits in the state
qubits in the state  sent through
sent through  phase shifters becomes
phase shifters becomes  .
When such a phase shifted state is un-entangled, using the reverse of
the entangling circuit, the
.
When such a phase shifted state is un-entangled, using the reverse of
the entangling circuit, the  controlled-{\sc not} gates leave the
state
controlled-{\sc not} gates leave the
state ![{\displaystyle |00\cdots 0{\rangle }[|0\rangle +e^{ni\phi }|1\rangle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6045fc2a6464b6cd42e9fb5c81084a169e808fda) , where the last
, where the last  qubits are left in
qubits are left in  , and the first qubit (the qubit used as the
control for the {\sc cnot} gates) is
, and the first qubit (the qubit used as the
control for the {\sc cnot} gates) is

Compare this state with that obtained from the single qubit
interferometer, Eq.(\ref{eq:l7-1qubitphase}); instead of a phase
 , the qubit now carries the phase
, the qubit now carries the phase  . This means that the
probability
. This means that the
probability  of measuring a single photon at the output becomes
of measuring a single photon at the output becomes

The standard deviation, from repeating this experiment, on average,
would be

Using  , we obtain for the uncertainty in
, we obtain for the uncertainty in  ,
,

which meets the Heisenberg limit.
Squeezed light interferometry
{{#lst:Squeezed light interferometry|content}}
Sensitivity to loss
Entangled states, while very useful for a wide variety of tasks,
including interferometry and metrology, are unfortunately generally
very fragile. In particular, entangled photon states degrade
quickly with due to loss.
Consider, for example, the two-qubit state  (suppressing
normalization). If one of theses photons goes through a
mostly-transmitting beamsplitter, then the photon may be lost; let us
say this happens with probability
(suppressing
normalization). If one of theses photons goes through a
mostly-transmitting beamsplitter, then the photon may be lost; let us
say this happens with probability  . If a photon is lost,
the state collapses into one with one remaining photon, say
. If a photon is lost,
the state collapses into one with one remaining photon, say  .
This is a product state -- no longer entangled. It is not even a
superposition. No photon is lost with probability
.
This is a product state -- no longer entangled. It is not even a
superposition. No photon is lost with probability  .
Even worse, if both modes suffer potential loss of a photon, then
no matter whcih mode looses a photon, the entangled state collapses;
this happens even if just one photon is lost. Thus, the
state retains some entanglement only with probability
.
Even worse, if both modes suffer potential loss of a photon, then
no matter whcih mode looses a photon, the entangled state collapses;
this happens even if just one photon is lost. Thus, the
state retains some entanglement only with probability
 .
And worst of all, if we have an
.
And worst of all, if we have an  -photon cat state
-photon cat state
 , and all modes are subject to loss
, and all modes are subject to loss
 , then useful entanglement is retained only with probability
, then useful entanglement is retained only with probability
 . Due to such loss, the phase measurement uncertainty
of an entangled state interferometer will go as
. Due to such loss, the phase measurement uncertainty
of an entangled state interferometer will go as

which is clearly undesirable.
Some physical systems, however, naturally suffer very little loss, and
can keep entangled states intact for long times. Photons
unfortunately do not have that feature, but certain atomic states,
such as hyperfine transitions, can be very long lived. Thus, many of
the concepts derived in the context of quantum states of light,
actually turn out to be more useful when applied to quantum states of
matter.








![{\displaystyle B={\frac {1}{\sqrt {2}}}\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e2d43ef535ef4f670f31b7ce4cfe7a15c1890f8)
![{\displaystyle [a,b]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcbe0f3bd3d712a823544cc4985e4dbd35b6967d)
![{\displaystyle \left[{\begin{array}{c}{a-ib}\\{b-ia}\end{array}}\right]=B\left[{\begin{array}{c}{a}\\{b}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74285e68d424d09733069d48c00a49acc738cec9)
![{\displaystyle P=\left[{\begin{array}{cc}{1}&{0}\\{0}&{e^{i\phi }}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f0a39e65796a1cc92d0a2ea729186ca5aca7a58)
![{\displaystyle {\begin{array}{rcl}U&=&BPB\\&=&{\frac {1}{2}}\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\left[{\begin{array}{cc}{1}&{0}\\{0}&{e^{i\phi }}\end{array}}\right]\left[{\begin{array}{cc}{1}&{-i}\\{-i}&{1}\end{array}}\right]\\&=&-ie^{i\phi /2}\left[{\begin{array}{cc}{\sin(\phi /2)}&{\cos(\phi /2)}\\{\cos(\phi /2)}&{-\sin(\phi /2)}\end{array}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aff63aa7808a03191a5315b3f548834ce336f41)


![{\displaystyle \left[{\begin{array}{c}{c}\\{d}\end{array}}\right]=U\left[{\begin{array}{c}{a}\\{b}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9786a4cebe3997ae8ab2e2a99556bd27a67b002)






















































![{\displaystyle |00\cdots 0{\rangle }[|0\rangle +e^{ni\phi }|1\rangle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6045fc2a6464b6cd42e9fb5c81084a169e808fda)












