Interferometry and metrology

Interferometry and metrology

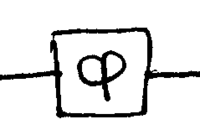
Suppose you are given a phase shifter of unknown $\phi$:

\noindent How accurately can you determine $\phi$, given a certain time, and laser power? In this section, we consider this basic measurement problem, and show how the usual shot noise limit can be exceeded by using quantum states of light, reaching a quantum limit determined by Heisenberg's uncertainty principle. This limit is achieved using entanglement, which can be realized using entangled multi-mode photons, or by a variety of squeezed states. The physics behind such quantum measurement techniques generalizes to a wide range of metrology problems, but a common challenge the need to reduce loss.

Heisenberg limit: entanglement

{{#lst:Interferometer Heisenberg limit|content}}

Squeezed light interferometry

{{#lst:Squeezed light interferometry|content}}

Sensitivity to loss

Entangled states, while very useful for a wide variety of tasks, including interferometry and metrology, are unfortunately generally very fragile. In particular, entangled photon states degrade quickly with due to loss. Consider, for example, the two-qubit state $|00{\rangle }+|11{\rangle }$ (suppressing normalization). If one of theses photons goes through a mostly-transmitting beamsplitter, then the photon may be lost; let us say this happens with probability $\epsilon$. If a photon is lost, the state collapses into one with one remaining photon, say $|10{\rangle }$. This is a product state -- no longer entangled. It is not even a superposition. No photon is lost with probability $(1-\epsilon )$. Even worse, if both modes suffer potential loss of a photon, then no matter whcih mode looses a photon, the entangled state collapses; this happens even if just one photon is lost. Thus, the state retains some entanglement only with probability $(1-\epsilon )^{2}$. And worst of all, if we have an $n$-photon cat state $|00\cdots 0{\rangle }+|11\cdots 1{\rangle }$, and all modes are subject to loss $\epsilon$, then useful entanglement is retained only with probability $(1-\epsilon )^{n}$. Due to such loss, the phase measurement uncertainty of an entangled state interferometer will go as

${\langle }\Delta \phi \rangle \sim {\frac {1}{n(1-\epsilon )^{n}}}\,,$

which is clearly undesirable. Some physical systems, however, naturally suffer very little loss, and can keep entangled states intact for long times. Photons unfortunately do not have that feature, but certain atomic states, such as hyperfine transitions, can be very long lived. Thus, many of the concepts derived in the context of quantum states of light, actually turn out to be more useful when applied to quantum states of matter.