Difference between revisions of "Tmp Lecture 23"
imported>Rouge |
imported>Rouge |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Clarification on coherence and dipole moment == | == Clarification on coherence and dipole moment == | ||
| Line 21: | Line 8: | ||
Next, consider a coherent light which is very weak. Monochromatic, coherent light is represented by a coherent state<math>|\alpha ></math> that has a Poissonian distribution of photon numbers: <math>|\alpha >=e^{-\frac{1}{2}|\alpha|^{2}} \sum_{n = 0}^{\infty } \frac{ \alpha^{n}}{\sqrt{n+1}} |n></math>. For <math>|\alpha | \ll 1 </math>, the population of the states with <math>n > 1</math> is negligible, and the atom prepared in a state <math>|g>+\epsilon |e></math> with <math>|\epsilon | \ll 1</math> emits a coherent state of light, in agreement with what is expected for small saturation. | Next, consider a coherent light which is very weak. Monochromatic, coherent light is represented by a coherent state<math>|\alpha ></math> that has a Poissonian distribution of photon numbers: <math>|\alpha >=e^{-\frac{1}{2}|\alpha|^{2}} \sum_{n = 0}^{\infty } \frac{ \alpha^{n}}{\sqrt{n+1}} |n></math>. For <math>|\alpha | \ll 1 </math>, the population of the states with <math>n > 1</math> is negligible, and the atom prepared in a state <math>|g>+\epsilon |e></math> with <math>|\epsilon | \ll 1</math> emits a coherent state of light, in agreement with what is expected for small saturation. | ||
| − | |||
| − | |||
| − | |||
== First observation of coherent population trapping CPT == | == First observation of coherent population trapping CPT == | ||
| − | ( | + | Prepare a multimode laser with regular frequency spacing (<math>v_1, \cdots</math>, in the figure). |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:Fig_CPT_convert_20100416042234.jpg]] | |
| − | + | Prepare a gas in a cylindrical volume with gradient of magnetic field in z direction, and observe fluorescence. | |
| − | + | Dark regions show the phaces where Zeeman shift between magnetic sublevels equals frequency difference between laser modes. | |
| − | |||
== Absorption calculation by interference, goin without inversion == | == Absorption calculation by interference, goin without inversion == | ||
| Line 46: | Line 25: | ||
It is commonly believed that we need <math>N_e > N_ g</math> for optical gain. But: Consider a V system with two unstable states that decay by coupling to the same continuum (This is a fairly special situation, e.g. different m-levels do not qualify, since they emit photons of different polarizations, thus the continue <math>|k_1></math> or <math>|k_2></math> are distinguishable.) | It is commonly believed that we need <math>N_e > N_ g</math> for optical gain. But: Consider a V system with two unstable states that decay by coupling to the same continuum (This is a fairly special situation, e.g. different m-levels do not qualify, since they emit photons of different polarizations, thus the continue <math>|k_1></math> or <math>|k_2></math> are distinguishable.) | ||
| − | + | [[Image:Fig_darkresonance_convert_20100416034152.jpg]] | |
| − | |||
Consider three level systems as in the figure where <math>|e_1></math> and <math>|e_2></math> decay to the continuum. A surprising feature of this system is the fact that there is a frequency at which the absorption rate becomes zero. To formally confirm this, we need to compute the second-order matrix element <math>M = \sum_{i =1 ,2} \frac{<continuum| V | e_i ><e_i | V |g> }{ \Delta_i - i \frac{\Gamma_i}{2}}</math>. Then, we know that there is a frequency at which this matrix element almost cancels. Let the frequency be <math>\omega _ o</math> that corresponds to an energy between the two levels. Note <math>\omega _ o</math> depends on the two matrix elements and we assume <math>(|\Delta_1| , |\Delta_2| \gg r_1, r_2</math>. | Consider three level systems as in the figure where <math>|e_1></math> and <math>|e_2></math> decay to the continuum. A surprising feature of this system is the fact that there is a frequency at which the absorption rate becomes zero. To formally confirm this, we need to compute the second-order matrix element <math>M = \sum_{i =1 ,2} \frac{<continuum| V | e_i ><e_i | V |g> }{ \Delta_i - i \frac{\Gamma_i}{2}}</math>. Then, we know that there is a frequency at which this matrix element almost cancels. Let the frequency be <math>\omega _ o</math> that corresponds to an energy between the two levels. Note <math>\omega _ o</math> depends on the two matrix elements and we assume <math>(|\Delta_1| , |\Delta_2| \gg r_1, r_2</math>. | ||
| − | |||
| − | |||
| − | |||
One may understand this by considering the fact that the two-photon scattering process <math>|g>\rightarrow |continuum></math> can proceed via two pathways that are fundamentally indistinguishable. In other words, it is impossible to tell whether it came from <math>|e_1></math> or <math>|e_2></math>. Thus, we need to consider quantum interference between them. | One may understand this by considering the fact that the two-photon scattering process <math>|g>\rightarrow |continuum></math> can proceed via two pathways that are fundamentally indistinguishable. In other words, it is impossible to tell whether it came from <math>|e_1></math> or <math>|e_2></math>. Thus, we need to consider quantum interference between them. | ||
| − | |||
| − | |||
| − | |||
| − | |||
Now assume that with some mechanism we populate, say, <math>|e_2></math> with a small number of atoms <math>N_2<N_ g</math>. These atoms have maximum stimulated emission probability on resonance, <math>|e_2>\rightarrow |g></math>, but there is also even larger absorption, since <math>N_ g>N_2</math>. However, because of the finite linewidth <math>r_2</math> of level <math>|e_2></math>, there is also stimulated emission gain at the "magical" (absorption-free) frequency <math>\omega _ o</math>. Since the <math>N_ g</math> atoms do not absorb here, there is net gain at this frequency in spite of <math>N_2<N_ g</math>, which can lead to "lasing without inversion." Note: this only works if the two excited states decay to the same continuum, such that the paths are indistinguishable. How can a system for lasing without inversion be realized? | Now assume that with some mechanism we populate, say, <math>|e_2></math> with a small number of atoms <math>N_2<N_ g</math>. These atoms have maximum stimulated emission probability on resonance, <math>|e_2>\rightarrow |g></math>, but there is also even larger absorption, since <math>N_ g>N_2</math>. However, because of the finite linewidth <math>r_2</math> of level <math>|e_2></math>, there is also stimulated emission gain at the "magical" (absorption-free) frequency <math>\omega _ o</math>. Since the <math>N_ g</math> atoms do not absorb here, there is net gain at this frequency in spite of <math>N_2<N_ g</math>, which can lead to "lasing without inversion." Note: this only works if the two excited states decay to the same continuum, such that the paths are indistinguishable. How can a system for lasing without inversion be realized? | ||
| Line 64: | Line 35: | ||
Possibility 1: hydrogen and dc electric field | Possibility 1: hydrogen and dc electric field | ||
| − | + | [[Image:Fig_examplessssss_convert_20100416034611.jpg]] | |
Possibility 2: use ac electric field to mix non-degenerate s state with p state. | Possibility 2: use ac electric field to mix non-degenerate s state with p state. | ||
| − | |||
== Electromagnetically induced transparency == | == Electromagnetically induced transparency == | ||
| Line 75: | Line 45: | ||
Radio Yerevan: "In principle yes, but you need another very powerful laser..." | Radio Yerevan: "In principle yes, but you need another very powerful laser..." | ||
| − | Steve Harris thought initially of special, ionizing excited states. However it is possible to realize the requirement of identical decay paths in a <math>lambda</math>-system with a a(strong) coupling laser. The phenomenon is closely related to coherent population trapping. | + | Steve Harris thought initially of special, ionizing excited states. However it is possible to realize the requirement of identical decay paths in a <math>\lambda</math>-system with a a(strong) coupling laser. The phenomenon is closely related to coherent population trapping. |
| − | |||
| − | |||
| − | + | [[Image:Fig_EIT1_convert_20100416040614.jpg]] | |
| − | + | For resonant fields <math>\omega _1=\omega _{ge}, \omega_2=\omega _{fe}</math>, we have | |
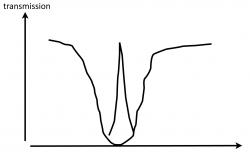
| − | + | [[Image:Fig_EIT2_convert_20100416040633.jpg]] | |
| − | + | As we turn up the power of the coupling laser the transmission improves and then broadens (in the realistic case of a finite decoherence rate <math>\gamma_{gf}=0</math>, an infinitesimally small coupling Rabi frequency, but the frequency window over which transmission occurs is very narrow and given by <math>\Delta \omega =\Omega_c</math>. | |
Latest revision as of 19:27, 15 April 2010
Contents
Clarification on coherence and dipole moment
Consider the coherence of the atom after coherent excitation with a short pulse (shorter than emission rate). Let the state of the atom be . Then, the coherence between and is maximum for , i.e. with pulse. (Coherence is in the density matrix. For a pure state, it is ). Now, let us consider a system with the atom and (external) EM mode. We consider the case where there is only a single EM mode coupled to the atom (ex, an atom strongly coupled to a cavity). Then, emission couples atomic states with photon number states: and . Thus, a pulse also maximizes the coherence and .
On the other hand, for continuous excitation (not a short pulse), saturation of the atom leads to emission of increasingly incoherent light (Mollow triplet). For Mollow triplet, see Cohen-Tannoudji p:424.
Next, consider a coherent light which is very weak. Monochromatic, coherent light is represented by a coherent state that has a Poissonian distribution of photon numbers: . For , the population of the states with is negligible, and the atom prepared in a state with emits a coherent state of light, in agreement with what is expected for small saturation.
First observation of coherent population trapping CPT
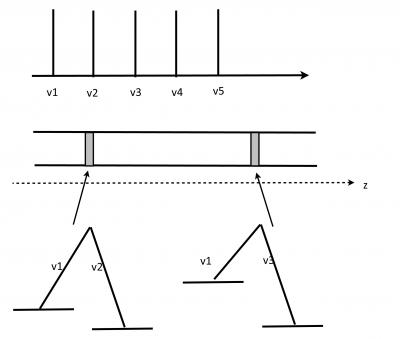
Prepare a multimode laser with regular frequency spacing (, in the figure).
Prepare a gas in a cylindrical volume with gradient of magnetic field in z direction, and observe fluorescence.
Dark regions show the phaces where Zeeman shift between magnetic sublevels equals frequency difference between laser modes.
Absorption calculation by interference, goin without inversion
(Steve Harris, PRL 62, 1033 (1989)) http://prl.aps.org/abstract/PRL/v62/i9/p1033_1
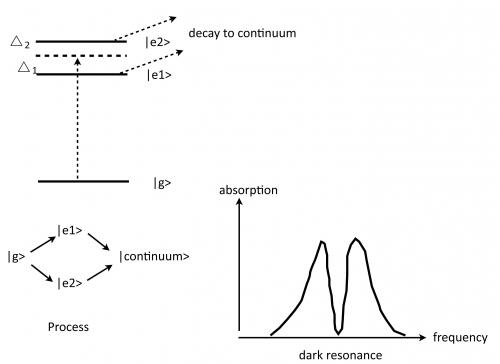
It is commonly believed that we need for optical gain. But: Consider a V system with two unstable states that decay by coupling to the same continuum (This is a fairly special situation, e.g. different m-levels do not qualify, since they emit photons of different polarizations, thus the continue or are distinguishable.)
Consider three level systems as in the figure where and decay to the continuum. A surprising feature of this system is the fact that there is a frequency at which the absorption rate becomes zero. To formally confirm this, we need to compute the second-order matrix element . Then, we know that there is a frequency at which this matrix element almost cancels. Let the frequency be that corresponds to an energy between the two levels. Note depends on the two matrix elements and we assume .
One may understand this by considering the fact that the two-photon scattering process can proceed via two pathways that are fundamentally indistinguishable. In other words, it is impossible to tell whether it came from or . Thus, we need to consider quantum interference between them.
Now assume that with some mechanism we populate, say, with a small number of atoms . These atoms have maximum stimulated emission probability on resonance, , but there is also even larger absorption, since . However, because of the finite linewidth of level , there is also stimulated emission gain at the "magical" (absorption-free) frequency . Since the atoms do not absorb here, there is net gain at this frequency in spite of , which can lead to "lasing without inversion." Note: this only works if the two excited states decay to the same continuum, such that the paths are indistinguishable. How can a system for lasing without inversion be realized?
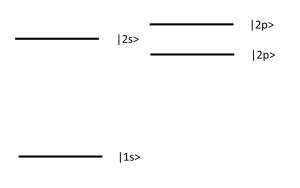
Possibility 1: hydrogen and dc electric field
Possibility 2: use ac electric field to mix non-degenerate s state with p state.
Electromagnetically induced transparency
"Is it possible to send a laser beam through a brick wall?"
Radio Yerevan: "In principle yes, but you need another very powerful laser..."
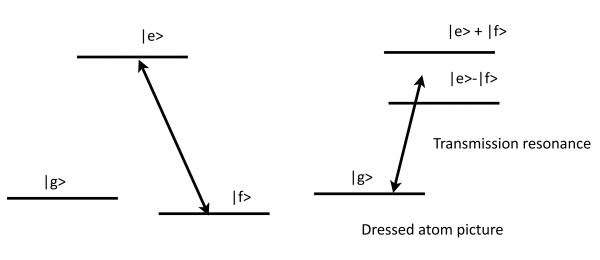
Steve Harris thought initially of special, ionizing excited states. However it is possible to realize the requirement of identical decay paths in a -system with a a(strong) coupling laser. The phenomenon is closely related to coherent population trapping.
For resonant fields , we have
As we turn up the power of the coupling laser the transmission improves and then broadens (in the realistic case of a finite decoherence rate , an infinitesimally small coupling Rabi frequency, but the frequency window over which transmission occurs is very narrow and given by .