Difference between revisions of "Poor man's entangler"
imported>Wikibot m (New page: How are entangled qubits generated in the laboratory? Entangled photons can be generated relatively simply, using downconversion and other nonlinear optics methods, as has been previously...) |
imported>Ichuang |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | How are entangled qubits generated in the laboratory? Entangled photons can be generated relatively simply, using downconversion and other nonlinear optics methods, as has been previously mentioned in the context of squeezed light. However, entangling states of matter is generally more difficult, although not as difficult as performing unitary quantum gates between matter qubits. This is because a probabilistic method, known as the "poor man's entangler," exists for generating entangled states, as we describe here for two atoms. | + | How are entangled qubits generated in the laboratory? Entangled |
| + | photons can be generated relatively simply, using downconversion and | ||
| + | other nonlinear optics methods, as has been previously mentioned in | ||
| + | the context of squeezed light. However, entangling states of matter | ||
| + | is generally more difficult, although not as difficult as performing | ||
| + | unitary quantum gates between matter qubits. This is because a | ||
| + | probabilistic method, known as the "poor man's entangler," exists | ||
| + | for generating entangled states, as we describe here for two atoms. | ||
| + | |||
| + | ==== Hong-Ou-Mandel Interference ==== | ||
| + | |||
Recall that a beamsplitter presented with the inputs <math>|1{\rangle}|1{\rangle}</math> | Recall that a beamsplitter presented with the inputs <math>|1{\rangle}|1{\rangle}</math> | ||
outputs <math>B_\theta|11 \rangle = (\cos^2\theta-\sin^2\theta)|11 \rangle + | outputs <math>B_\theta|11 \rangle = (\cos^2\theta-\sin^2\theta)|11 \rangle + | ||
| − | \sqrt{2}\cos\theta\sin\theta(|20{\rangle}-|02 \rangle )</math>. | + | \sqrt{2}\cos\theta\sin\theta(|20{\rangle}-|02 \rangle )</math>. When the beamspliter is |
| + | 50/50, that is, <math>\theta=\pi/4</math>, the output is | ||
| + | <math>(|02{\rangle}+|20 \rangle )/\sqrt{2}</math>, so that both photons always appear | ||
| + | together (reference Hong-Ou-Mandel interferometers). | ||
| + | |||
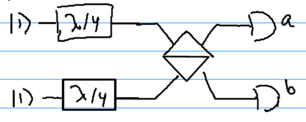
| + | Imagine, now, that we send in polarized photons, but into a 50/50 | ||
| + | non-polarized beamsplitter: | ||
::[[Image:Poor_man_entangler-qbs_with_pol.png|thumb|306px|none|]] | ::[[Image:Poor_man_entangler-qbs_with_pol.png|thumb|306px|none|]] | ||
| + | Moreover, let | ||
| + | there be circular polarizers before the inputs, so that the input | ||
| + | <math>|\psi_{in}{\rangle}</math> to the beamspliter is the state (suppressing | ||
| + | normalizations) | ||
| + | :<math>\begin{array}{rcl} | ||
| + | |\psi_{in} \rangle &=& \left[ { |H{\rangle}+|V \rangle } \right] \otimes \left[ { |H{\rangle}+|V \rangle } \right] | ||
| + | \\ | ||
| + | &=& |HH \rangle + |HV \rangle + |VH \rangle + |VV{\rangle} | ||
| + | \,. | ||
| + | \end{array}</math> | ||
| + | Now, if there are two photon number resolving detectors at the | ||
| + | outputs, the only way for both detectors to sense a single photon is | ||
| + | if the input polarizations are <math>HV</math> or <math>VH</math>, because otherwise the two | ||
| + | input photons would go the same direction. | ||
| + | |||
| + | ==== Probabilistic entanglement generation via beamsplitter ==== | ||
| + | |||
| + | An atom can be prepared in such a way that it will emit a polarized | ||
| + | photon and be left in a spin state (<math>|U{\rangle}</math> or <math>|D{\rangle}</math>) which is | ||
| + | identical to the polarization emitted (<math>|H{\rangle}</math> or <math>|V{\rangle}</math>, | ||
| + | respectively). Moreover, this can be in a superposition, such that | ||
| + | the joint state of the atom and emitted photon is <math>|UH \rangle + |DV{\rangle}</math>. | ||
| + | |||
| + | Let the input to the beamsplitter be given by two such atoms, such | ||
| + | that | ||
| + | :<math>\begin{array}{rcl} | ||
| + | |\psi_{in} \rangle &=& \left[ { |UH{\rangle}+|DV \rangle } \right] \otimes \left[ { |UH{\rangle}+|DV \rangle } \right] | ||
| + | \\ | ||
| + | &=& |UU\,HH \rangle + |UD\,HV \rangle + |DU\,VH \rangle + |DD\,VV{\rangle} | ||
| + | \,. | ||
| + | \end{array}</math> | ||
| + | Just as before, the only cases in which two single photons are | ||
| + | measured at the output of the beamsplitter are those for which the two | ||
| + | input and output photon polarizations are opposite. Of course, two | ||
| + | photons could appear in one of the output, but if that happens the | ||
| + | protocol fails and has to be re-started), | ||
| + | |||
| + | In particular, the only output states amplitudes which lead to single | ||
| + | photons in each of the two outputs are | ||
| + | :<math> | ||
| + | |\psi_{out} \rangle = |UD \rangle (|01{\rangle}+|10 \rangle )_H (|01{\rangle}-|10 \rangle )_V | ||
| + | + |DU \rangle (|01{\rangle}+|10 \rangle )_V (|01{\rangle}-|10 \rangle _H | ||
| + | \,. | ||
| + | </math> | ||
| + | Here, <math>(|01{\rangle}+|10 \rangle )_H</math> means that the <math>a</math> and <math>b</math> outputs are in a | ||
| + | superposition of one horizontally polarized photon appearing in the | ||
| + | two modes, and similarly for the other terms. | ||
| + | |||
| + | This means there are two possible cases for single photons to appear | ||
| + | at both the <math>a</math> and <math>b</math> outputs. If <math>a=1H</math> and <math>b=1V</math> (where <math>1H</math> | ||
| + | means a single horizontally polarized photon is detected, and | ||
| + | similarly for <math>1V</math>), then the post-measurement state of the two atoms | ||
| + | is <math>|{\rm atoms} \rangle = |UD{\rangle}-|DU{\rangle}</math>, because both the <math>|UD{\rangle}</math> and | ||
| + | <math>|DU{\rangle}</math> states of atoms could lead to such an outcome, and they are | ||
| + | indistinguishable due to the mixing of the beamsplitter. The only | ||
| + | other possibility is for <math>a=1V</math> and <math>b=1H</math>, which would leave a | ||
| + | post-measurement atomic state of <math>-|UD \rangle + |DU{\rangle}</math>. This is identical | ||
| + | to <math>|{\rm atoms}{\rangle}</math>, up to a global phase, which is irrelevant. | ||
| + | |||
| + | Thus, when two single photons are detected in coincidence at the | ||
| + | output of the beamsplitter, the atoms are known to be left in the | ||
| + | maximally entangled state | ||
| + | :<math> | ||
| + | \frac{|UD{\rangle}-|DU{\rangle}}{\sqrt{2}} | ||
| + | \,. | ||
| + | </math> | ||
| + | |||
| + | ==== Post-selected entanglement generation: experiment ==== | ||
| + | |||
| + | This is a rather inefficient way to generate entangled states of | ||
| + | atoms, experimentally, because it is difficult to persuade two atoms | ||
| + | to emit their photons at times sufficiently close to make the photons | ||
| + | indistinguishable. | ||
| + | |||
| + | However, the scheme is otherwise so simple to implement that it can be | ||
| + | worthwhile. Such a scheme has been used to demonstrate a violation of | ||
| + | the CHSH inequality with no "detection loophole," meaning that the | ||
| + | measurement probabilities were sufficiently high so as not to admit a | ||
| + | probabilistic clasical explanation based on detector inefficiency. | ||
| + | The same scheme also produced sufficiently highly entangled states for | ||
| + | a demonstration of teleportation of matter qubits. | ||
| + | |||
| + | <!-- | ||
| + | * <refbase>5243</refbase> | ||
| + | * <refbase>5244</refbase> | ||
| + | * <refbase>5235</refbase> | ||
| + | --> | ||
Latest revision as of 02:31, 2 February 2017
How are entangled qubits generated in the laboratory? Entangled photons can be generated relatively simply, using downconversion and other nonlinear optics methods, as has been previously mentioned in the context of squeezed light. However, entangling states of matter is generally more difficult, although not as difficult as performing unitary quantum gates between matter qubits. This is because a probabilistic method, known as the "poor man's entangler," exists for generating entangled states, as we describe here for two atoms.
Hong-Ou-Mandel Interference
Recall that a beamsplitter presented with the inputs outputs . When the beamspliter is 50/50, that is, , the output is , so that both photons always appear together (reference Hong-Ou-Mandel interferometers).
Imagine, now, that we send in polarized photons, but into a 50/50 non-polarized beamsplitter:
Moreover, let there be circular polarizers before the inputs, so that the input to the beamspliter is the state (suppressing normalizations)
Now, if there are two photon number resolving detectors at the outputs, the only way for both detectors to sense a single photon is if the input polarizations are or , because otherwise the two input photons would go the same direction.
Probabilistic entanglement generation via beamsplitter
An atom can be prepared in such a way that it will emit a polarized photon and be left in a spin state ( or ) which is identical to the polarization emitted ( or , respectively). Moreover, this can be in a superposition, such that the joint state of the atom and emitted photon is .
Let the input to the beamsplitter be given by two such atoms, such that
Just as before, the only cases in which two single photons are measured at the output of the beamsplitter are those for which the two input and output photon polarizations are opposite. Of course, two photons could appear in one of the output, but if that happens the protocol fails and has to be re-started),
In particular, the only output states amplitudes which lead to single photons in each of the two outputs are
Here, means that the and outputs are in a superposition of one horizontally polarized photon appearing in the two modes, and similarly for the other terms.
This means there are two possible cases for single photons to appear at both the and outputs. If and (where means a single horizontally polarized photon is detected, and similarly for ), then the post-measurement state of the two atoms is , because both the and states of atoms could lead to such an outcome, and they are indistinguishable due to the mixing of the beamsplitter. The only other possibility is for and , which would leave a post-measurement atomic state of . This is identical to , up to a global phase, which is irrelevant.
Thus, when two single photons are detected in coincidence at the output of the beamsplitter, the atoms are known to be left in the maximally entangled state
Post-selected entanglement generation: experiment
This is a rather inefficient way to generate entangled states of atoms, experimentally, because it is difficult to persuade two atoms to emit their photons at times sufficiently close to make the photons indistinguishable.
However, the scheme is otherwise so simple to implement that it can be worthwhile. Such a scheme has been used to demonstrate a violation of the CHSH inequality with no "detection loophole," meaning that the measurement probabilities were sufficiently high so as not to admit a probabilistic clasical explanation based on detector inefficiency. The same scheme also produced sufficiently highly entangled states for a demonstration of teleportation of matter qubits.





![{\displaystyle {\begin{array}{rcl}|\psi _{in}\rangle &=&\left[{|H{\rangle }+|V\rangle }\right]\otimes \left[{|H{\rangle }+|V\rangle }\right]\\&=&|HH\rangle +|HV\rangle +|VH\rangle +|VV{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2347fc6273958788e02e92c087bb578ccf25553)







![{\displaystyle {\begin{array}{rcl}|\psi _{in}\rangle &=&\left[{|UH{\rangle }+|DV\rangle }\right]\otimes \left[{|UH{\rangle }+|DV\rangle }\right]\\&=&|UU\,HH\rangle +|UD\,HV\rangle +|DU\,VH\rangle +|DD\,VV{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ade24779065d3f50b6379d91c24e37bfd58e8ab)















