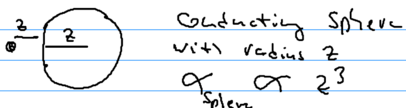Difference between revisions of "Van der Waals interaction"
imported>Juliar |
imported>Jschloss |
||
| (14 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Today - the Van der Waals interaction between two atoms. Two physical | + | <categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;" hideprefix=auto>8.422</categorytree> |
| + | |||
| + | Today - the Van der Waals interaction between two atoms. | ||
| + | |||
| + | In this course, we mainly discuss single atoms, or many atoms. This chapter is an exception --- we discuss interactions between two atoms. There are several reasons for it: The van der Waals force belongs to the class of Casimir forces, which can be regarded as either being due to the exchange of virtual photons, or due to the modified zero-point energy of the electromagnetic field. We will present both viewpoints. The latter has attracted recent interest in the search for the origin of the dark energy of the universe. A second reason to discuss van der Waals forces is that it provides a non-trivial example for the power of the diagrammatic approach, and finally, it shows how the exchange of virtual photons can lead to attraction. So we can encounter in AMO physics an example for forces mediated by virtual exchange of field quanta. | ||
| + | |||
| + | === Two physical pictures of the van der Waals interaction: classical and quantum === | ||
| + | |||
| + | Two physical | ||
pictures illuminate the richness of the problem. Consider two atoms | pictures illuminate the richness of the problem. Consider two atoms | ||
<math>a</math> and <math>b</math> separated by distance <math>R</math>. The Coulomb interaction | <math>a</math> and <math>b</math> separated by distance <math>R</math>. The Coulomb interaction | ||
| Line 9: | Line 17: | ||
Integrating leaves us with two interacting dipoles | Integrating leaves us with two interacting dipoles | ||
:<math> | :<math> | ||
| − | H' = \frac{1}{R^3}( \vec{d}_a \vec{d}_b-3(\vec{d}_a \cdot \hat{R} | + | H' = \frac{1}{R^3}( \vec{d}_a \cdot \vec{d}_b-3(\vec{d}_a \cdot \hat{R} ) ( |
| − | \vec{d_b}\cdot \hat{R}) | + | \vec{d_b}\cdot \hat{R}) ) |
\,. | \,. | ||
</math> | </math> | ||
| Line 26: | Line 34: | ||
\,. | \,. | ||
</math> | </math> | ||
| + | |||
| + | ==== Physical interpretation ==== | ||
| + | |||
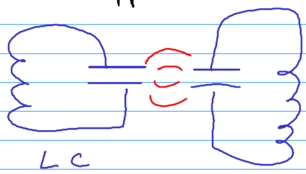
Let us interpret this result now (see Kleppner's class notes) - the | Let us interpret this result now (see Kleppner's class notes) - the | ||
physics of the van der Waals interaction are all due to quantum | physics of the van der Waals interaction are all due to quantum | ||
fluctuations. Consider two resonant circuits that are capactively | fluctuations. Consider two resonant circuits that are capactively | ||
| − | coupled. | + | coupled: |
| + | ::[[Image:vdw-fig1.png|thumb|306px|none|]] | ||
| + | The coupling goes as <math>1/R^3</math>. Each resonator has frequency | ||
<math>\omega_0</math>, and classically coupled oscillators split their | <math>\omega_0</math>, and classically coupled oscillators split their | ||
frequencies, giving | frequencies, giving | ||
| Line 36: | Line 49: | ||
\,. | \,. | ||
</math> | </math> | ||
| − | + | The ground state energy is <math> \hbar(\omega_+ + \omega_-)/2 </math>. The two <math>1/R^3</math> add up to zero leaving just the <math>1/R^6</math> term. | |
| − | <math>1/R^6</math> term | + | |
An equivalent description focusing on the atomic dipole moment is as | An equivalent description focusing on the atomic dipole moment is as | ||
follows. A neutral atom has no expectation for the dipole operator, | follows. A neutral atom has no expectation for the dipole operator, | ||
| Line 55: | Line 68: | ||
\,. | \,. | ||
</math> | </math> | ||
| + | |||
| + | ==== Origin in fluctuations of the electromagnetic field ==== | ||
| + | |||
So far, we've neglected fluctuations of the electromagnetic field. | So far, we've neglected fluctuations of the electromagnetic field. | ||
What could the vacuum fluctuations of the field do to neutral atoms? | What could the vacuum fluctuations of the field do to neutral atoms? | ||
| Line 73: | Line 89: | ||
about this. Conceptually, one sums over all modes of the | about this. Conceptually, one sums over all modes of the | ||
electromagnetic field - this time in free space, without the boundary | electromagnetic field - this time in free space, without the boundary | ||
| − | condition as we | + | condition as we do in the Casimir force case. The long wavelengths |
do not average out to zero, when they are of wavelength comparable to | do not average out to zero, when they are of wavelength comparable to | ||
the distance between the two atoms. Their contribution, when density | the distance between the two atoms. Their contribution, when density | ||
| Line 83: | Line 99: | ||
So how does the <math>1/R^6</math> term disappear? If you focus on the | So how does the <math>1/R^6</math> term disappear? If you focus on the | ||
fluctuations of the instantaneous dipole moments, then you get | fluctuations of the instantaneous dipole moments, then you get | ||
| − | <math>1/R^6</math>; this is | + | <math>1/R^6</math>; this is the correct result for short range interactions. |
It can be derived, as we showed above, by conceptually using the | It can be derived, as we showed above, by conceptually using the | ||
| − | uncertainty principle for the | + | uncertainty principle for the atomic dipoles. In contrast, when the |
uncertainty principle for the electromagnetic field is used, we get a | uncertainty principle for the electromagnetic field is used, we get a | ||
<math>1/R^7</math> force; this is applicable at long ranges, and is known as the | <math>1/R^7</math> force; this is applicable at long ranges, and is known as the | ||
Casimir-Polder effect, or the retarded van der Waals interaction. | Casimir-Polder effect, or the retarded van der Waals interaction. | ||
| − | Note that a | + | Note that a full quantum theory of both atoms and field are needed to |
get both of these interactions properly. The crossover distance | get both of these interactions properly. The crossover distance | ||
between the two interactions is set by <math>R\sim \lambda_{res}</math>, the | between the two interactions is set by <math>R\sim \lambda_{res}</math>, the | ||
| Line 99: | Line 115: | ||
moment, and also no fluctuations - the classical van der Waals force | moment, and also no fluctuations - the classical van der Waals force | ||
is zero. But quantum-mechanically, vacuum fluctuations are always | is zero. But quantum-mechanically, vacuum fluctuations are always | ||
| − | present | + | present. It doesn't cost extra energy to create them. For the van der Waals force, the dipole fluctuations simply become correlated and lower the total energy of the system (by leading to an attractive interaction energy). |
| − | === | + | |
| + | |||
| + | === Van der Waals forces due to absorption and emission of virtual photons === | ||
| + | |||
Returning to our theme of perturbation theory for this chapter, let us | Returning to our theme of perturbation theory for this chapter, let us | ||
| − | consider the van der Waals interaction from a | + | consider the van der Waals interaction from a diagrammatic approach. |
(This follows API pp 121-126). The fundamental idea is an exchange of | (This follows API pp 121-126). The fundamental idea is an exchange of | ||
virtual photons. | virtual photons. | ||
| Line 113: | Line 132: | ||
because they were determined by the charges and not a degree of | because they were determined by the charges and not a degree of | ||
freedom, and we kept the transverse fields, as the radiation field. | freedom, and we kept the transverse fields, as the radiation field. | ||
| − | In the qualitative discussion above, we | + | In the qualitative discussion above, we obtained the dipole moments <math>\vec{d}</math> and their interactions from a Coulomb integral. However, in our QED approach, outside the neutral atoms there only exists the radiation field. We want to understand now how this can result in the van der Waals interaction. |
| − | + | ||
| − | + | The only way two neutral atoms can interact with each other is by | |
| − | |||
| − | |||
exchange of virtual photons. See Cohen-Tanoudji for hundreds of pages | exchange of virtual photons. See Cohen-Tanoudji for hundreds of pages | ||
of illuminative discussion about this. | of illuminative discussion about this. | ||
| − | + | ||
The language of Feynman diagrams can be used to understand the van der | The language of Feynman diagrams can be used to understand the van der | ||
Waals interaction. Consider two identical atoms spaced apart by | Waals interaction. Consider two identical atoms spaced apart by | ||
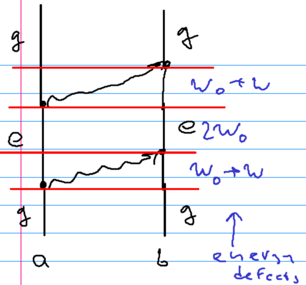
| Line 129: | Line 146: | ||
photon, which is absorbed by the second one, returning both atoms to | photon, which is absorbed by the second one, returning both atoms to | ||
the ground state: | the ground state: | ||
| − | ::[[Image: | + | ::[[Image:vdw-fig2.png|thumb|306px|none|]] |
This picture indicates that to leading order, we need diagrams with | This picture indicates that to leading order, we need diagrams with | ||
two photons, and four vertices. The dominant contribution comes from | two photons, and four vertices. The dominant contribution comes from | ||
photons with <math>\lambda\sim D</math>, that is <math>\omega\sim 2\pi c/D</math>. Another | photons with <math>\lambda\sim D</math>, that is <math>\omega\sim 2\pi c/D</math>. Another | ||
| − | important piece of | + | important piece of guidance is that the virtual process is admixing |
| − | + | states of higher energy to the ground state, lowering the total energy; energy shifts in second order processes | |
go as | go as | ||
:<math> | :<math> | ||
| Line 140: | Line 157: | ||
\,, | \,, | ||
</math> | </math> | ||
| − | characterizing the | + | characterizing the smaller amplitude of mixing with higher energy |
| − | states. With extra intermediate states | + | states. With extra intermediate states this becomes |
:<math> | :<math> | ||
\Delta E \sim \frac{V_{lk}V_{kj} V_{0i}}{(E_l-E_k)(E_i-E_j)} | \Delta E \sim \frac{V_{lk}V_{kj} V_{0i}}{(E_l-E_k)(E_i-E_j)} | ||
| Line 147: | Line 164: | ||
</math> | </math> | ||
When we emit virtual photons, there are two energies involved; | When we emit virtual photons, there are two energies involved; | ||
| − | one is <math>\omega_0</math>, one is the exchanged photon energy. The energy | + | one is the atomic excitation energy <math>\omega_0</math>, the other one is the exchanged photon energy <math>\omega</math>. The energy |
defects in the above picture are thus as shown in the figure above: | defects in the above picture are thus as shown in the figure above: | ||
initially <math>\omega_0+\omega</math>, then <math>2\omega_0</math>, then | initially <math>\omega_0+\omega</math>, then <math>2\omega_0</math>, then | ||
<math>\omega_0+\omega</math>. | <math>\omega_0+\omega</math>. | ||
| + | |||
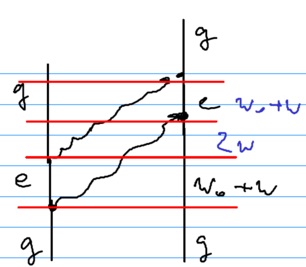
A second diagram involved is as if one atom emitted two photons | A second diagram involved is as if one atom emitted two photons | ||
simultaneously: | simultaneously: | ||
| − | ::[[Image: | + | ::[[Image:vdw-fig3.png|thumb|306px|none|]] |
Which of these two diagrams is preferable depends on how large | Which of these two diagrams is preferable depends on how large | ||
| Line 160: | Line 178: | ||
energy defects in the three regions are <math>\omega+\omega_0</math>, then | energy defects in the three regions are <math>\omega+\omega_0</math>, then | ||
<math>2\omega</math> (versus <math>2\omega_0</math> for the first diagram), and then | <math>2\omega</math> (versus <math>2\omega_0</math> for the first diagram), and then | ||
| − | <math>\omega+\omega_0</math> | + | <math>\omega+\omega_0</math>. |
| − | |||
| − | + | The contribution of each diagram is proportional | |
| − | |||
| − | |||
| − | |||
| − | |||
to the inverse product of the energy defects: | to the inverse product of the energy defects: | ||
:<math> | :<math> | ||
| − | H_{ | + | H_{first} \sim |
\frac{1}{\omega_0+\omega}\frac{1}{2\omega_0}\frac{1}{\omega_0+\omega} | \frac{1}{\omega_0+\omega}\frac{1}{2\omega_0}\frac{1}{\omega_0+\omega} | ||
| − | + | ||
\,. | \,. | ||
</math> | </math> | ||
In contrast, for the second diagram, we get | In contrast, for the second diagram, we get | ||
:<math> | :<math> | ||
| − | H_{ | + | H_{second} \sim |
| − | \ | + | \frac{1}{\omega_0+\omega}\frac{1}{2\omega}\frac{1}{\omega_0+\omega} |
\,. | \,. | ||
</math> | </math> | ||
| + | |||
| + | Focusing on these two diagrams, let us consider what happens at short | ||
| + | and long ranges. Let <math>\lambda_0</math> be the wavelength of the radiation. | ||
| + | Short range is defined by <math>D\ll \lambda_0</math> (meaning <math>\omega\gg | ||
| + | \omega_0</math>), and long range is <math>D\gg \lambda_0</math> (meaning | ||
| + | <math>\omega\ll\omega_0</math>). Thus for short range, the first diagram dominates, whereas for long range, the second. | ||
Thus, going from long range to short range involves an additional | Thus, going from long range to short range involves an additional | ||
factor of <math>\omega</math> in the interaction. Since <math>\omega \sim 1/D</math>, this | factor of <math>\omega</math> in the interaction. Since <math>\omega \sim 1/D</math>, this | ||
| Line 186: | Line 205: | ||
=== Casimir forces revisted === | === Casimir forces revisted === | ||
| + | Let us now look at Casimir forces for different systems. | ||
| + | |||
Consider three scenarios: | Consider three scenarios: | ||
| − | * | + | * Atom-atom. At long distances <math>V\propto |
\frac{\alpha_1\alpha_2}{R^7}</math>. | \frac{\alpha_1\alpha_2}{R^7}</math>. | ||
| − | * | + | * Atom-wall. Recall that the polarizibility of an atom has units of volume, <math>R^3</math>. A large metal sphere also has polarizability <math>R^3</math>. Thus, at long distances, <math>V\propto\frac{\alpha R^3}{R^7} \sim\frac{\alpha}{R^4}</math>. |
| − | Recall that the polarizibility of an atom has units of volume, <math>R^3</math>. | + | ::[[Image:vdw-fig4.png|thumb|406px|none|]] |
| − | A large metal sphere also has polarizability <math>R^3</math>. Thus, at long | + | * Two walls. Two walls can be regarded as two spheres, with a radius similar to their distance. The potential is now 1/R, but we have to normalize it to the area <math>\frac{V}{A}\propto \frac{1}{R R^2} \sim \frac{1}{R^3}</math>. |
| − | distances, <math>V\propto\frac{\alpha R^3}{R^7} \sim\frac{\alpha}{R^4}</math>. | + | ::[[Image:vdw-fig5.png|thumb|506px|none|]] |
| − | * two | ||
| − | |||
At short distances: | At short distances: | ||
| − | * | + | Both the atom-atom and the atom-wall interaction change in the power law by one factor of R, whereas the wall-wall interaction is always in the far field (A metallic wall corresponds to an atom with high excitation energy and therefore small wavelength). |
| − | * | + | |
| − | * | + | * Atom-atom. <math>V\sim\frac{1}{R^6}</math> |
| + | * Atom-wall. <math>V\sim\frac{1}{R^3}</math> | ||
| + | * Two walls. Always in the far field. | ||
=== References === | === References === | ||
[[Category:Photon-atom interactions]] | [[Category:Photon-atom interactions]] | ||
| + | |||
| + | * see API pp. 121-126 | ||
| + | * [http://cua.mit.edu/8.422/HANDOUTS/VanDerWaalsInteraction.pdf four pages course notes from Dan Kleppner] | ||
| + | * [http://cua.mit.edu/8.422/HANDOUTS/Retarded...long-range%20potentials.pdf Physics Today paper by L. Spruch (Nov. 1986, p. 37)] | ||
Latest revision as of 18:12, 30 March 2015
Today - the Van der Waals interaction between two atoms.
In this course, we mainly discuss single atoms, or many atoms. This chapter is an exception --- we discuss interactions between two atoms. There are several reasons for it: The van der Waals force belongs to the class of Casimir forces, which can be regarded as either being due to the exchange of virtual photons, or due to the modified zero-point energy of the electromagnetic field. We will present both viewpoints. The latter has attracted recent interest in the search for the origin of the dark energy of the universe. A second reason to discuss van der Waals forces is that it provides a non-trivial example for the power of the diagrammatic approach, and finally, it shows how the exchange of virtual photons can lead to attraction. So we can encounter in AMO physics an example for forces mediated by virtual exchange of field quanta.
Contents
Two physical pictures of the van der Waals interaction: classical and quantum
Two physical pictures illuminate the richness of the problem. Consider two atoms and separated by distance . The Coulomb interaction between these is
Integrating leaves us with two interacting dipoles
In the quantum picture, these dipoles become operators. First order perturbation theory tells us that if one atom is excited and the other is in the ground state, this gives an interaction term
But if both atoms are in the ground state, then the leading term is given by second order perturbation theory, as
Physical interpretation
Let us interpret this result now (see Kleppner's class notes) - the physics of the van der Waals interaction are all due to quantum fluctuations. Consider two resonant circuits that are capactively coupled:
The coupling goes as . Each resonator has frequency , and classically coupled oscillators split their frequencies, giving
The ground state energy is . The two add up to zero leaving just the term.
An equivalent description focusing on the atomic dipole moment is as follows. A neutral atom has no expectation for the dipole operator, , but the variance for this is nonzero, . This is just as the simple harmonic oscillator in its ground state has zero , but nonzero in the ground state. The fluctuating dipole moment of atom creates a fluctuating field at position ,
This induces a dipole in atom . The interaction energy between two dipoles is
Origin in fluctuations of the electromagnetic field
So far, we've neglected fluctuations of the electromagnetic field. What could the vacuum fluctuations of the field do to neutral atoms? Fluctuations at position and can induce dipole moments, since the atoms are polarizable:
The corresponding interaction is
See Larry Spuch, Physics Today article, posted on web site for more about this. Conceptually, one sums over all modes of the electromagnetic field - this time in free space, without the boundary condition as we do in the Casimir force case. The long wavelengths do not average out to zero, when they are of wavelength comparable to the distance between the two atoms. Their contribution, when density of states are included, and cutoff appropriately, gives
So how does the term disappear? If you focus on the fluctuations of the instantaneous dipole moments, then you get ; this is the correct result for short range interactions. It can be derived, as we showed above, by conceptually using the uncertainty principle for the atomic dipoles. In contrast, when the uncertainty principle for the electromagnetic field is used, we get a force; this is applicable at long ranges, and is known as the Casimir-Polder effect, or the retarded van der Waals interaction. Note that a full quantum theory of both atoms and field are needed to get both of these interactions properly. The crossover distance between the two interactions is set by , the resonant wavelength of that atoms.
The entirety of the van der Waals interaction is a quantum phenomenon (thus, the reason your table is solid is because of quantum mechanics!). Classically, there is no average value of the dipole moment, and also no fluctuations - the classical van der Waals force is zero. But quantum-mechanically, vacuum fluctuations are always present. It doesn't cost extra energy to create them. For the van der Waals force, the dipole fluctuations simply become correlated and lower the total energy of the system (by leading to an attractive interaction energy).
Van der Waals forces due to absorption and emission of virtual photons
Returning to our theme of perturbation theory for this chapter, let us consider the van der Waals interaction from a diagrammatic approach. (This follows API pp 121-126). The fundamental idea is an exchange of virtual photons. The Hamiltonian in the dipole approximation is
In deriving the QED Hamiltonian, we discarded the longidutional fields because they were determined by the charges and not a degree of freedom, and we kept the transverse fields, as the radiation field. In the qualitative discussion above, we obtained the dipole moments and their interactions from a Coulomb integral. However, in our QED approach, outside the neutral atoms there only exists the radiation field. We want to understand now how this can result in the van der Waals interaction.
The only way two neutral atoms can interact with each other is by exchange of virtual photons. See Cohen-Tanoudji for hundreds of pages of illuminative discussion about this.
The language of Feynman diagrams can be used to understand the van der Waals interaction. Consider two identical atoms spaced apart by distance . The atoms initially start in state , the ground state. One emits a virtual photon, going into a virtual excited state (with an energy below the ground state). This photon is absorbed by the second atom. After a short time, the first atom emits another photon, which is absorbed by the second one, returning both atoms to the ground state:
This picture indicates that to leading order, we need diagrams with two photons, and four vertices. The dominant contribution comes from photons with , that is . Another important piece of guidance is that the virtual process is admixing states of higher energy to the ground state, lowering the total energy; energy shifts in second order processes go as
characterizing the smaller amplitude of mixing with higher energy states. With extra intermediate states this becomes
When we emit virtual photons, there are two energies involved; one is the atomic excitation energy , the other one is the exchanged photon energy . The energy defects in the above picture are thus as shown in the figure above: initially , then , then .
A second diagram involved is as if one atom emitted two photons simultaneously:
Which of these two diagrams is preferable depends on how large is compared to . Ultimately, that distinguishes short and long range interactions, and versus . The energy defects in the three regions are , then (versus for the first diagram), and then .
The contribution of each diagram is proportional to the inverse product of the energy defects:
In contrast, for the second diagram, we get
Focusing on these two diagrams, let us consider what happens at short and long ranges. Let be the wavelength of the radiation. Short range is defined by (meaning ), and long range is (meaning ). Thus for short range, the first diagram dominates, whereas for long range, the second. Thus, going from long range to short range involves an additional factor of in the interaction. Since , this gives the change from to in the potential.
Casimir forces revisted
Let us now look at Casimir forces for different systems.
Consider three scenarios:
- Atom-atom. At long distances .
- Atom-wall. Recall that the polarizibility of an atom has units of volume, . A large metal sphere also has polarizability . Thus, at long distances, .
- Two walls. Two walls can be regarded as two spheres, with a radius similar to their distance. The potential is now 1/R, but we have to normalize it to the area .
At short distances:
Both the atom-atom and the atom-wall interaction change in the power law by one factor of R, whereas the wall-wall interaction is always in the far field (A metallic wall corresponds to an atom with high excitation energy and therefore small wavelength).
- Atom-atom.
- Atom-wall.
- Two walls. Always in the far field.