Difference between revisions of "Entangled Photons"
imported>Ichuang |
imported>Ketterle |
||
| (15 intermediate revisions by 2 users not shown) | |||
| Line 30: | Line 30: | ||
| − | === Definition === | + | === Definition of entanglement === |
A bi-partite (or, in the language of light, "two-mode") state | A bi-partite (or, in the language of light, "two-mode") state | ||
<math>|\psi \rangle _{AB}</math> of a composite system is entangled if and only if | <math>|\psi \rangle _{AB}</math> of a composite system is entangled if and only if | ||
| Line 38: | Line 38: | ||
\,. | \,. | ||
</math> | </math> | ||
| − | Note that "<math>\otimes</math>" denotes a tensor product. Being a | + | Note that "<math>\otimes</math>" denotes a tensor product. Being a ''composite system'' means that there should be a tensor product |
| − | composite system | ||
structure to the Hilbert space -- more on this point later. | structure to the Hilbert space -- more on this point later. | ||
| + | |||
| + | ==== Examples ==== | ||
| + | |||
Some examples will help illustrate this definition: | Some examples will help illustrate this definition: | ||
| Line 47: | Line 49: | ||
* <math>\frac{|00{\rangle}+|01{\rangle}+|10{\rangle}+|11{\rangle}}{{2}}</math> is unentangled, because it is equal to <math>\frac{|0{\rangle}+|1{\rangle}}{\sqrt{2}}\otimes \frac{|0{\rangle}+|1{\rangle}}{\sqrt{2}}</math> | * <math>\frac{|00{\rangle}+|01{\rangle}+|10{\rangle}+|11{\rangle}}{{2}}</math> is unentangled, because it is equal to <math>\frac{|0{\rangle}+|1{\rangle}}{\sqrt{2}}\otimes \frac{|0{\rangle}+|1{\rangle}}{\sqrt{2}}</math> | ||
* <math>\frac{|00{\rangle}+|01{\rangle}+|11{\rangle}}{\sqrt{3}}</math> is what? Work this out. | * <math>\frac{|00{\rangle}+|01{\rangle}+|11{\rangle}}{\sqrt{3}}</math> is what? Work this out. | ||
| + | |||
| + | ==== Mixed states ==== | ||
A similar definition holds for mixed states. A bi-partite mixed state | A similar definition holds for mixed states. A bi-partite mixed state | ||
| Line 60: | Line 64: | ||
the pure state case, however, so we will focus our attention on | the pure state case, however, so we will focus our attention on | ||
developing an understanding by studying pure state entanglement. | developing an understanding by studying pure state entanglement. | ||
| + | |||
| + | ==== Standard 2-qubit entangled states ==== | ||
The most basic entangled state in Nature is that of two | The most basic entangled state in Nature is that of two | ||
| Line 75: | Line 81: | ||
present. | present. | ||
| − | The EPR state <math>|\psi_{EPR}{\rangle}</math> must be of | + | The EPR state <math>|\psi_{EPR}{\rangle}</math> must be of ''two physically distinct |
| − | systems | + | systems''. This is because the definition of entanglement specifies |
that entanglement is a property of a composite system, made of | that entanglement is a property of a composite system, made of | ||
two (or more) parts, rather than just a single system. It is | two (or more) parts, rather than just a single system. It is | ||
important that in principle, the two parts can be separately | important that in principle, the two parts can be separately | ||
manipulated and measured, for entanglement to be meaningfully defined. | manipulated and measured, for entanglement to be meaningfully defined. | ||
| + | |||
| + | ==== Examples: experimental systems ==== | ||
For example, the two electrons in the ground state of a helium atom | For example, the two electrons in the ground state of a helium atom | ||
| Line 86: | Line 94: | ||
helium atoms are all entangled? Absolutely not, under normal circumstances. Without an | helium atoms are all entangled? Absolutely not, under normal circumstances. Without an | ||
experimental situation in which the two electrons in the atom can be | experimental situation in which the two electrons in the atom can be | ||
| − | individually manipulated, | + | individually manipulated, they have no meaningful entanglement. |
A meaningful photon representation of <math>|\psi_{EPR}{\rangle}</math> is given, for | A meaningful photon representation of <math>|\psi_{EPR}{\rangle}</math> is given, for | ||
| Line 117: | Line 125: | ||
results: | results: | ||
::[[Image:chapter2-quantum-light-part-4-qm-bell3-fig.png|thumb|500px|none|]] | ::[[Image:chapter2-quantum-light-part-4-qm-bell3-fig.png|thumb|500px|none|]] | ||
| + | |||
| + | ==== CHSH Inequality ==== | ||
Classical statistics places a bound on the correlation of the | Classical statistics places a bound on the correlation of the | ||
| Line 122: | Line 132: | ||
that the choice of measurements is random. In particular, consider | that the choice of measurements is random. In particular, consider | ||
the quantity <math>QS+RS+RT-QT</math>. Notice that | the quantity <math>QS+RS+RT-QT</math>. Notice that | ||
| − | + | {{Eq | |
| + | |math=<math>\begin{array}{rcl} | ||
QS+RS+RT-QT & = & (Q+R)S +(R-Q)T | QS+RS+RT-QT & = & (Q+R)S +(R-Q)T | ||
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| + | |num=3.1 | ||
| + | }} | ||
Because <math>R, Q = \pm 1</math> it follows that either <math>(Q+R)S = 0</math> or <math>(R-Q)T | Because <math>R, Q = \pm 1</math> it follows that either <math>(Q+R)S = 0</math> or <math>(R-Q)T | ||
= 0</math>. In either case, it is easy to see | = 0</math>. In either case, it is easy to see | ||
| − | from | + | from (3.1) that <math>QS+RS+RT-QT = \pm 2</math>. |
Suppose next that <math>p(q,r,s,t)</math> is the probability that, before the | Suppose next that <math>p(q,r,s,t)</math> is the probability that, before the | ||
| Line 135: | Line 148: | ||
prepared, and on experimental noise. Letting <math> E (\cdot)</math> denote the | prepared, and on experimental noise. Letting <math> E (\cdot)</math> denote the | ||
mean value of a quantity, we have | mean value of a quantity, we have | ||
| − | + | {{Eq | |
| + | |math=<math>\begin{array}{rcl} | ||
E (QS+RS+RT-QT) & = & \sum_{qrst} p(q,r,s,t) ( qs+rs+rt-qt ) \\ & | E (QS+RS+RT-QT) & = & \sum_{qrst} p(q,r,s,t) ( qs+rs+rt-qt ) \\ & | ||
\leq & \sum_{qrst} p(q,r,s,t) \times 2 \\ & = & 2. | \leq & \sum_{qrst} p(q,r,s,t) \times 2 \\ & = & 2. | ||
\end{array}</math> | \end{array}</math> | ||
| + | |num=3.2 | ||
| + | }} | ||
Also, | Also, | ||
| − | + | {{Eq | |
| + | |math=<math>\begin{array}{rcl} | ||
E (QS+RS+RT-QT) & = & \sum_{qrst} p(q,r,s,t) qs + \sum_{qrst} | E (QS+RS+RT-QT) & = & \sum_{qrst} p(q,r,s,t) qs + \sum_{qrst} | ||
p(q,r,s,t) rs \\ & & + \sum_{qrst} p(q,r,s,t) rt - | p(q,r,s,t) rs \\ & & + \sum_{qrst} p(q,r,s,t) rt - | ||
| Line 146: | Line 163: | ||
E (RT)- E (QT). | E (RT)- E (QT). | ||
\end{array}</math> | \end{array}</math> | ||
| − | Comparing | + | |num=3.3 |
| + | }} | ||
| + | Comparing (3.2) and (3.3) we | ||
obtain the Bell inequality, | obtain the Bell inequality, | ||
| − | + | {{Eq | |
| − | + | |math=<math> E (QS)+ E (RS)+ E (RT)- E (QT) \leq 2 </math> | |
| − | + | |num=3.4 | |
| − | + | }} | |
This result is also often known as the CHSH inequality | This result is also often known as the CHSH inequality | ||
| − | after the initials of its four discoverers. It is part | + | after the initials of its four discoverers (It is named after John Clauser, Michael Horne, Abner Shimony and Richard Holt, who described it in a much-cited paper published in 1969). It is part |
of a larger set of inequalities known generically as Bell | of a larger set of inequalities known generically as Bell | ||
| − | inequalities, since the first was found by John | + | inequalities, since the first was found by John Bell. |
| + | |||
| + | ==== Quantum violation of CHSH inequality ==== | ||
When an experiment is performed, however, a result violating this | When an experiment is performed, however, a result violating this | ||
| Line 168: | Line 189: | ||
and Bob's be | and Bob's be | ||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
| − | S &=& \ | + | S &=& \frac{ {- |0 \rangle \langle 0| - |0 \rangle \langle 1| - |1 \rangle \langle 0| + |1 \rangle \langle 1|} }{\sqrt{2}} |
| − | \\ T &=& \ | + | \\ T &=& \frac{ {+ |0 \rangle \langle 0| - |0 \rangle \langle 1| - |1 \rangle \langle 0| - |1 \rangle \langle 1|} }{ \sqrt{2}} |
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| Line 195: | Line 216: | ||
\end{array}</math> | \end{array}</math> | ||
This result is in direct contradiction with the bound established by | This result is in direct contradiction with the bound established by | ||
| − | classical statistics, Eq. | + | classical statistics, Eq.(3.4), which predicts that the |
average value of <math>QS</math> plus the average value of <math>RS</math> plus the average | average value of <math>QS</math> plus the average value of <math>RS</math> plus the average | ||
value of <math>RT</math> minus the average value of <math>QT</math> can never exceed two. | value of <math>RT</math> minus the average value of <math>QT</math> can never exceed two. | ||
| Line 201: | Line 222: | ||
Yet here, quantum mechanics predicts that this sum of averages yields | Yet here, quantum mechanics predicts that this sum of averages yields | ||
<math>2 \sqrt 2</math>, and indeed, this is observed experimentally! | <math>2 \sqrt 2</math>, and indeed, this is observed experimentally! | ||
| + | |||
| + | ==== Implications for the classical world ==== | ||
| + | |||
The main implication of this result is that one of the assumptions | The main implication of this result is that one of the assumptions | ||
behind the classical bound was wrong. The two most often | behind the classical bound was wrong. The two most often | ||
| Line 208: | Line 232: | ||
* The assumption that Alice performing her measurement does not influence the result of Bob's measurement (and vice versa). This is sometimes known as the assumption of locality. | * The assumption that Alice performing her measurement does not influence the result of Bob's measurement (and vice versa). This is sometimes known as the assumption of locality. | ||
| − | These two together are known as the assumptions of | + | These two together are known as the assumptions of ''local realism''. An important lesson from experiments with EPR states is that either or both of locality and realism must be dropped from our view of the world if we are to develop a good intuitive understanding of quantum mechanics. |
| − | realism | + | |
| − | that either or both of locality and realism must be dropped from our | + | === Poor man's entangler === |
| − | view of the world if we are to develop a good intuitive understanding | + | |
| − | of quantum mechanics. | + | {{:Poor man's entangler}} |
=== Superdense coding === | === Superdense coding === | ||
| Line 218: | Line 242: | ||
inspired a great search to discover useful tasks which can be | inspired a great search to discover useful tasks which can be | ||
accomplished more efficiently using entangled states than by using | accomplished more efficiently using entangled states than by using | ||
| − | just classical resources. Teleportation is one example. Another, | + | just classical resources. [[Non-classical_states_of_light#Teleportation_of_light|Teleportation is one example]]. Another, |
example is superdense coding, a protocol through which Alice can | example is superdense coding, a protocol through which Alice can | ||
communicate two bits of classical information to Bob, by sending him | communicate two bits of classical information to Bob, by sending him | ||
| Line 302: | Line 326: | ||
such that a final measurement in the usual ("computational") basis | such that a final measurement in the usual ("computational") basis | ||
returns the two classical bits <math>k_1k_0</math> which Alice sent. | returns the two classical bits <math>k_1k_0</math> which Alice sent. | ||
| + | |||
=== Purification === | === Purification === | ||
Entangled states are useful. So far, however, we've mainly | Entangled states are useful. So far, however, we've mainly | ||
| Line 328: | Line 353: | ||
</math> | </math> | ||
with some unknown (but constant) value of <math>a</math> and <math>b</math>. They may turn | with some unknown (but constant) value of <math>a</math> and <math>b</math>. They may turn | ||
| − | these into useful Bell pairs by doing the following. Take two | + | these into useful Bell pairs by doing the following. Take two poorly |
entangled states, | entangled states, | ||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
| Line 350: | Line 375: | ||
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| − | Now Alice and Bob each measure the qubits in the target pair. With | + | Note that in this notation, Alice has qubits 1 and 3, and Bob 2 and 4. |
| + | Now Alice and Bob each measure the qubits in the target pair (i.e. qubits 3 and 4). With | ||
probability <math>2|ab|^2</math>, they will obtain <math>11</math> as their result, in which | probability <math>2|ab|^2</math>, they will obtain <math>11</math> as their result, in which | ||
case the post-measurement state is <math>|\Phi^+ \rangle = | case the post-measurement state is <math>|\Phi^+ \rangle = | ||
| Line 370: | Line 396: | ||
reduced density matrix of one-half of an entangled bi-partite state, | reduced density matrix of one-half of an entangled bi-partite state, | ||
in the following way. | in the following way. | ||
| + | |||
| + | ==== Partial Traces ==== | ||
| + | |||
Given <math>|\psi_{AB}{\rangle}</math>, the partial trace over <math>B</math> is the density matrix | Given <math>|\psi_{AB}{\rangle}</math>, the partial trace over <math>B</math> is the density matrix | ||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
| Line 384: | Line 413: | ||
</math> | </math> | ||
the completely mixed state. | the completely mixed state. | ||
| + | |||
| + | ==== Von Neumann Entropy ==== | ||
| + | |||
The randomness of a quantum state <math>\rho</math> is measured by the {\em Von | The randomness of a quantum state <math>\rho</math> is measured by the {\em Von | ||
Neumann entropy}, <math>S(\rho)</math>, defined as | Neumann entropy}, <math>S(\rho)</math>, defined as | ||
| Line 397: | Line 429: | ||
Note that the entropy of a pure state is zero. For the completely | Note that the entropy of a pure state is zero. For the completely | ||
mixed state in the example above, <math>S(\rho_A) = 1</math> bit. | mixed state in the example above, <math>S(\rho_A) = 1</math> bit. | ||
| + | |||
| + | ==== The Entanglement ==== | ||
| + | |||
The Entanglement <math>E(|\psi_{AB} \rangle )</math> of a bi-partite quantum state | The Entanglement <math>E(|\psi_{AB} \rangle )</math> of a bi-partite quantum state | ||
<math>|\psi_{AB}{\rangle}</math> is defined as being the entropy of one of the reduced | <math>|\psi_{AB}{\rangle}</math> is defined as being the entropy of one of the reduced | ||
| Line 406: | Line 441: | ||
Since <math>|\psi_{AB}{\rangle}</math> is a pure state, these two entropies must be | Since <math>|\psi_{AB}{\rangle}</math> is a pure state, these two entropies must be | ||
equal. | equal. | ||
| + | |||
The Entanglement of the Bell states is the maximum possible for any | The Entanglement of the Bell states is the maximum possible for any | ||
two-qubit state: <math>E(|\Phi^\pm \rangle ) = E(|\Psi^\pm \rangle ) = 1</math>. In fact, we | two-qubit state: <math>E(|\Phi^\pm \rangle ) = E(|\Psi^\pm \rangle ) = 1</math>. In fact, we | ||
Latest revision as of 05:22, 19 April 2009
Entanglement is the essence of the most "quantum" nature of quantum states of light. Albert Einstein studied it, together with Boris Podolsky and Nathan Rosen, and argued that properties of entangled quantum states demonstrated that quantum mechanics could not be a complete theory of nature, because of violations of intuition. Experiments now validate such violations, and we appreciate that intuition from classical mechanics is what is at fault. Indeed, John Bell proved that correlations produced by entangled quantum states are distinctly beyond what is possible with classical mechanics. Today, we also understand that entanglement is useful for many things. Ideally, it can allow measurement with precision greater than with classical states; entanglement can also be used to increase communication rates through noisy channels, and indeed, even make it possible when noise rates are otherwise too high. Entanglement also enables exponential speedup of the solution of certain mathematical problems, through quantum computation. And, as we have seen, it allows new protocols such as teleportation; entanglement also makes possible new games, sometimes providing more optimal Nash equilibria in important multi-party economic scenarios such as the tragedy of the commons.
In this section, we define entanglement, describe some of its non-classical properties, illustrate an application of entanglement to speeding up communication, and show how pure entangled states can be purified from imperfect ones. We then conclude by describing some measures of entanglement.
Contents
Definition of entanglement
A bi-partite (or, in the language of light, "two-mode") state of a composite system is entangled if and only if there do not exist and such that
Note that "" denotes a tensor product. Being a composite system means that there should be a tensor product structure to the Hilbert space -- more on this point later.
Examples
Some examples will help illustrate this definition:
- is unentangled
- is entangled (verify this for yourself!)
- is unentangled, because it is equal to
- is what? Work this out.
Mixed states
A similar definition holds for mixed states. A bi-partite mixed state of a composite system is entangled if and only if there do not exist states and of and , and probabilities , satisfying , such that
Mixed state entanglement is considerably more difficult to study than the pure state case, however, so we will focus our attention on developing an understanding by studying pure state entanglement.
Standard 2-qubit entangled states
The most basic entangled state in Nature is that of two two-dimensional systems. One such entangled state is the well known singlet state,
This state, or states with essentially the same properties, can be produced with photons. However, is not just a single photon. Indeed, one photon input a beamsplitter can easily produce the state , as we have previously seen, but in that situation is a vacuum state, with no photons present.
The EPR state must be of two physically distinct systems. This is because the definition of entanglement specifies that entanglement is a property of a composite system, made of two (or more) parts, rather than just a single system. It is important that in principle, the two parts can be separately manipulated and measured, for entanglement to be meaningfully defined.
Examples: experimental systems
For example, the two electrons in the ground state of a helium atom are naturally in a singlet ; does this mean helium atoms are all entangled? Absolutely not, under normal circumstances. Without an experimental situation in which the two electrons in the atom can be individually manipulated, they have no meaningful entanglement.
A meaningful photon representation of is given, for example, by the polarization of two photons. Two photons can be generated by down-conversion, such that their polarizations have the state
where and indicate horizontal and vertical polarization.
Another example is two photons, each of which can exist in one of two modes, such that we may identify , and . The state
is a meaningfully entangled state, since each photon can be manipulated and measured separately.
EPR and the Bell inequality
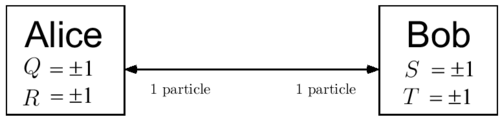
What about entanglement is uniquely quantum-mechanical? This question can be answered with the following experiment, which measures correlations produced by measurements of an EPR pair. Let there be two parties, Alice and Bob, who are each given one photon from some state (which may be quantum or classical). Alice and Bob each simultaneously measure in random bases: Alice measures either or , and Bob measures either or , obtaining for their results:
CHSH Inequality
Classical statistics places a bound on the correlation of the measurement outcomes, independent of , given the fact that the choice of measurements is random. In particular, consider the quantity . Notice that
(3.1)
Because it follows that either or . In either case, it is easy to see from (3.1) that .
Suppose next that is the probability that, before the measurements are performed, the system is in a state where , and . These probabilities may depend on how is prepared, and on experimental noise. Letting denote the mean value of a quantity, we have
(3.2)
Also,
(3.3)
Comparing (3.2) and (3.3) we obtain the Bell inequality,
(3.4)
This result is also often known as the CHSH inequality after the initials of its four discoverers (It is named after John Clauser, Michael Horne, Abner Shimony and Richard Holt, who described it in a much-cited paper published in 1969). It is part of a larger set of inequalities known generically as Bell inequalities, since the first was found by John Bell.
Quantum violation of CHSH inequality
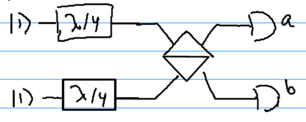
When an experiment is performed, however, a result violating this inequality is obtained for certain input states. Specifically, suppose that the state distributed to Alice and Bob is the entangled two-photon state . Also, let Alice's measurement operators be
and Bob's be
Physically, if the EPR pair is represented by photon polarizations, so that , then and correspond to measurements of linear and circular photon polarization, while and are the same measurements but only after rotating the polarization by . In the dual-rail representation, these measurement operators correspond to four well defined configurations of beamsplitters and phase shifters, followed by photodetectors.
Denoting expectation values using , we find that
Thus,
This result is in direct contradiction with the bound established by classical statistics, Eq.(3.4), which predicts that the average value of plus the average value of plus the average value of minus the average value of can never exceed two.
Yet here, quantum mechanics predicts that this sum of averages yields , and indeed, this is observed experimentally!
Implications for the classical world
The main implication of this result is that one of the assumptions behind the classical bound was wrong. The two most often questioned are
- The assumption that the physical properties of the state have definite values which exist independent of observation. This is sometimes known as the assumption of realism.
- The assumption that Alice performing her measurement does not influence the result of Bob's measurement (and vice versa). This is sometimes known as the assumption of locality.
These two together are known as the assumptions of local realism. An important lesson from experiments with EPR states is that either or both of locality and realism must be dropped from our view of the world if we are to develop a good intuitive understanding of quantum mechanics.
Poor man's entangler
How are entangled qubits generated in the laboratory? Entangled photons can be generated relatively simply, using downconversion and other nonlinear optics methods, as has been previously mentioned in the context of squeezed light. However, entangling states of matter is generally more difficult, although not as difficult as performing unitary quantum gates between matter qubits. This is because a probabilistic method, known as the "poor man's entangler," exists for generating entangled states, as we describe here for two atoms.
Hong-Ou-Mandel Interference
Recall that a beamsplitter presented with the inputs outputs . When the beamspliter is 50/50, that is, , the output is , so that both photons always appear together (reference Hong-Ou-Mandel interferometers).
Imagine, now, that we send in polarized photons, but into a 50/50 non-polarized beamsplitter:
Moreover, let there be circular polarizers before the inputs, so that the input to the beamspliter is the state (suppressing normalizations)
Now, if there are two photon number resolving detectors at the outputs, the only way for both detectors to sense a single photon is if the input polarizations are or , because otherwise the two input photons would go the same direction.
Probabilistic entanglement generation via beamsplitter
An atom can be prepared in such a way that it will emit a polarized photon and be left in a spin state ( or ) which is identical to the polarization emitted ( or , respectively). Moreover, this can be in a superposition, such that the joint state of the atom and emitted photon is .
Let the input to the beamsplitter be given by two such atoms, such that
Just as before, the only cases in which two single photons are measured at the output of the beamsplitter are those for which the two input and output photon polarizations are opposite. Of course, two photons could appear in one of the output, but if that happens the protocol fails and has to be re-started),
In particular, the only output states amplitudes which lead to single photons in each of the two outputs are
Here, means that the and outputs are in a superposition of one horizontally polarized photon appearing in the two modes, and similarly for the other terms.
This means there are two possible cases for single photons to appear at both the and outputs. If and (where means a single horizontally polarized photon is detected, and similarly for ), then the post-measurement state of the two atoms is , because both the and states of atoms could lead to such an outcome, and they are indistinguishable due to the mixing of the beamsplitter. The only other possibility is for and , which would leave a post-measurement atomic state of . This is identical to , up to a global phase, which is irrelevant.
Thus, when two single photons are detected in coincidence at the output of the beamsplitter, the atoms are known to be left in the maximally entangled state
Post-selected entanglement generation: experiment
This is a rather inefficient way to generate entangled states of atoms, experimentally, because it is difficult to persuade two atoms to emit their photons at times sufficiently close to make the photons indistinguishable.
However, the scheme is otherwise so simple to implement that it can be worthwhile. Such a scheme has been used to demonstrate a violation of the CHSH inequality with no "detection loophole," meaning that the measurement probabilities were sufficiently high so as not to admit a probabilistic clasical explanation based on detector inefficiency. The same scheme also produced sufficiently highly entangled states for a demonstration of teleportation of matter qubits.
Superdense coding
The fact that entanglement has distinctly non-classical properties has inspired a great search to discover useful tasks which can be accomplished more efficiently using entangled states than by using just classical resources. Teleportation is one example. Another, example is superdense coding, a protocol through which Alice can communicate two bits of classical information to Bob, by sending him just one qubit, given prior shared entanglement. This works as follows. Let Alice and Bob each have half of the entangled state
This state is presumed to have been distributed to each party, long before Alice obtains the classical information she wishes to communicate to Bob. Let the information Alice wishes to send be the two bits . She performs one of four rotations to her local quantum state, depending on , as follows:
where , , and are the usual Pauli matrices (they happen to also be unitary transforms, and that is how they are used here). The state after Alice's operation is thus (suppressing normalization factors, and labeling states by , so Alice's state is written on the right):
Alice now sends her state to Bob, so that he ends up with both halves. Now, since these four states are mutually orthogonal, they can be distinguished from each other by projective measurements. To be explicit, it is useful to introduce a common operation and some common nomenclature used in quantum information. The two-level systems we have been working with are known as being "qubits," and as we saw in Section 2.3, using dual-rail photon representations of qubits, one qubit can be used as a control to flip another qubit (eg using a nonlinear Mach-Zehnder interferometer). Such a "controlled-{\sc not}" operation implements the following unitary transform:
Mathematically, this is easy to remember as being the map . The procedure Bob uses to distinguish his four measurements can then be described as being a controlled-{\sc not} operation (also known as a "{\sc cnot}"), followed by a Hadamard gate on the control qubit, which we recall performs
Specifically, for the four states, the controlled-{\sc not} gives:
Note that these four states factorize, eg . Bob next performs a Hadamard gate to the left qubit, obtaining
such that a final measurement in the usual ("computational") basis returns the two classical bits which Alice sent.
Purification
Entangled states are useful. So far, however, we've mainly encountered a few particular entangled states in our applications, teleportation, and superdense coding, and in violating Bell's inequality. These are the maximally entangled states, and there are four standard ones (known as "Bell state") used as basis states:
On the other hand, we've noticed that there are many entangled two-qubit states. In fact, generically is entangled for all non-trivial values of and . Going even further, it turns out most multi-partite states, drawn randomly, are entangled! In a moment, we will try to quantify how entangled each are. But first, it is useful to motivate this quest by showing that in fact, arbitrary entangled qubit pairs can be turned into a standard Bell state, at some cost. Suppose that Alice and Bob have a large supply of poorly entangled states
with some unknown (but constant) value of and . They may turn these into useful Bell pairs by doing the following. Take two poorly entangled states,
Now Alice and Bob each perform a controlled-{\sc not} operation on the two qubits they locally possess. This transforms , and , and leaves all other states unchanged, giving a new state
Note that in this notation, Alice has qubits 1 and 3, and Bob 2 and 4. Now Alice and Bob each measure the qubits in the target pair (i.e. qubits 3 and 4). With probability , they will obtain as their result, in which case the post-measurement state is , a perfect Bell pair. Otherwise, if they obtain , they throw away the result and start again. This protocol allows Alice and Bob to purify Bell states from poorly entangled states, albeit rather inefficiently. Efficient procedures do exist, and they can be read about in the literature (see, for example, Section 12.5 of {\em Quantum Computation and Quantum Information}, by Nielsen and Chuang).
Measures
There are several good measures of how entangled a pure state is. The basic idea is that entangled qubits are correlated, so that the individual qubits of an entangled pair are highly random. Moreover, the more entangled a pair is, the more random the separated qubits should be.
This randomness can be measured by computing the entropy of the reduced density matrix of one-half of an entangled bi-partite state, in the following way.
Partial Traces
Given , the partial trace over is the density matrix
Similarly, is the partial trace over . For example, for ,
the completely mixed state.
Von Neumann Entropy
The randomness of a quantum state is measured by the {\em Von Neumann entropy}, , defined as
where are the eigenvalues of . Note that this entropy is measured in units of bits, since the logs are taken to have base . Note that the entropy of a pure state is zero. For the completely mixed state in the example above, bit.
The Entanglement
The Entanglement of a bi-partite quantum state is defined as being the entropy of one of the reduced density matrices:
Since is a pure state, these two entropies must be equal.
The Entanglement of the Bell states is the maximum possible for any two-qubit state: . In fact, we use the Bell states to define the unit of entanglement, the {\em ebit}. Recall from the last subsection that less-entangled quantum states can be purified to produce pure ebits. In fact, the turns out to be the rate at which can be purified to become ebits. Entanglement is thus fungible, and can act much like a currency, useful for a variety of applications, and convertible into various denominations. It truly is thus a physical resource.



































































![{\displaystyle {\begin{array}{rcl}|\psi _{in}\rangle &=&\left[{|H{\rangle }+|V\rangle }\right]\otimes \left[{|H{\rangle }+|V\rangle }\right]\\&=&|HH\rangle +|HV\rangle +|VH\rangle +|VV{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2347fc6273958788e02e92c087bb578ccf25553)







![{\displaystyle {\begin{array}{rcl}|\psi _{in}\rangle &=&\left[{|UH{\rangle }+|DV\rangle }\right]\otimes \left[{|UH{\rangle }+|DV\rangle }\right]\\&=&|UU\,HH\rangle +|UD\,HV\rangle +|DU\,VH\rangle +|DD\,VV{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ade24779065d3f50b6379d91c24e37bfd58e8ab)


































![{\displaystyle {\begin{array}{rcl}|\psi {\rangle }\otimes |\psi {\rangle }&=&\left[{a|00{\rangle }+b|11\rangle }\right]\left[{a|00{\rangle }+b|11\rangle }\right]\\&=&a|00\rangle \left[{a|00{\rangle }+b|11\rangle }\right]+b|11\rangle \left[{a|00{\rangle }+b|11\rangle }\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4e7dd38f7083c33f87ef6de8247e0e89b197b0)


![{\displaystyle {\begin{array}{rcl}a|00\rangle \left[{a|00{\rangle }+b|11\rangle }\right]+b|11\rangle \left[{a|11{\rangle }+b|00\rangle }\right]=\left[{a^{2}|00\rangle +b^{2}|11\rangle }\right]|00\rangle +ab\left[{|00\rangle +|11\rangle }\right]|11{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5afb70d0755b5625d24a05155328bb161b4e5a2c)








![{\displaystyle \rho _{A}=\rho _{B}={\frac {1}{2}}\left[{\begin{array}{cc}{1}&{0}\\{0}&{1}\end{array}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d6226a05c377e92933e3700c33dad123c6c9d51)










