Difference between revisions of "Non-classical states of light"
imported>Ichuang |
imported>Ichuang |
||
| (25 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;">8.422</categorytree> | ||
| − | |||
One of the most special properties of the coherent state is that its | One of the most special properties of the coherent state is that its | ||
fluctuations in <math>P</math> and <math>Q</math> are equal, and minimal, meaning that it | fluctuations in <math>P</math> and <math>Q</math> are equal, and minimal, meaning that it | ||
| Line 14: | Line 14: | ||
experimentally detected, then show how it can be useful in a quantum | experimentally detected, then show how it can be useful in a quantum | ||
experiment: teleportation. | experiment: teleportation. | ||
| + | |||
=== Classical squeezing === | === Classical squeezing === | ||
We are interested in the dynamics of the simple harmonic oscillator, | We are interested in the dynamics of the simple harmonic oscillator, | ||
| Line 19: | Line 20: | ||
considering the classical oscillator. Consider a particle in the | considering the classical oscillator. Consider a particle in the | ||
potential | potential | ||
| − | + | <math> | |
V(x) = \frac{1}{2} m\omega_0^2 x^2 | V(x) = \frac{1}{2} m\omega_0^2 x^2 | ||
| − | + | ||
</math> | </math> | ||
The equations of motion for this particle, <math>\ddot{x}(t) = -\omega_0^2 x(t)</math> | The equations of motion for this particle, <math>\ddot{x}(t) = -\omega_0^2 x(t)</math> | ||
| Line 34: | Line 35: | ||
where <math>r(t)</math>, <math>c(t)</math>, and <math>s(t)</math> are constant. This motion is circular: | where <math>r(t)</math>, <math>c(t)</math>, and <math>s(t)</math> are constant. This motion is circular: | ||
::[[Image:chapter2-quantum-light-part-2-lect5-classical-squeezing.png|thumb|306px|none|]] | ::[[Image:chapter2-quantum-light-part-2-lect5-classical-squeezing.png|thumb|306px|none|]] | ||
| + | |||
Suppose a small, "parametric" driving force is added, analogous to | Suppose a small, "parametric" driving force is added, analogous to | ||
kicking while on a swing. For a swinging pendulum, this force could | kicking while on a swing. For a swinging pendulum, this force could | ||
| Line 46: | Line 48: | ||
</math> | </math> | ||
where <math>\epsilon</math> is small. | where <math>\epsilon</math> is small. | ||
| − | + | [[Image:20070321-003722_pritchard-squeezing.png|frame|right|Prof. Dave Pritchard demonstrating classical squeezing with a parametrically driven pendulum oscillator [https://www.youtube.com/watch?v=_CiRfjrc8aw see video]]] | |
| − | + | ||
| + | Substituting | ||
| + | the above ansatz for <math>x(t)</math> into the equation of motion | ||
:<math> | :<math> | ||
\ddot{x} = -\omega_0^2 \left[ { 1+\epsilon \sin 2\omega_0 t } \right] x(t) | \ddot{x} = -\omega_0^2 \left[ { 1+\epsilon \sin 2\omega_0 t } \right] x(t) | ||
| Line 70: | Line 74: | ||
parametric drive to become elliptical: | parametric drive to become elliptical: | ||
::[[Image:chapter2-quantum-light-part-2-lect5-classical-squeezing2.png|thumb|200px|none|]] | ::[[Image:chapter2-quantum-light-part-2-lect5-classical-squeezing2.png|thumb|200px|none|]] | ||
| + | |||
What is the ultimate limit of this classical squeezing effect? The | What is the ultimate limit of this classical squeezing effect? The | ||
answer turns out to be quantum noise, which enforces the Heisenberg | answer turns out to be quantum noise, which enforces the Heisenberg | ||
uncertainty limit, <math>\Delta P\,\Delta Q\geq \hbar/2</math>. | uncertainty limit, <math>\Delta P\,\Delta Q\geq \hbar/2</math>. | ||
| + | |||
=== Squeezed states: quantum === | === Squeezed states: quantum === | ||
A quantum simple harmonic oscillator excited by a parametric drive at | A quantum simple harmonic oscillator excited by a parametric drive at | ||
| Line 84: | Line 90: | ||
two photons at <math>\omega_0</math> and <math>\omega_0</math>, due to cascaded decay from | two photons at <math>\omega_0</math> and <math>\omega_0</math>, due to cascaded decay from | ||
two equaly spaced energy levels: | two equaly spaced energy levels: | ||
| − | ::[[Image:chapter2-quantum-light-part-2-lect5-opo.png|thumb| | + | ::[[Image:chapter2-quantum-light-part-2-lect5-opo.png|thumb|400px|none|]] |
| + | |||
Such a process can be described by the Hamiltonian | Such a process can be described by the Hamiltonian | ||
:<math> | :<math> | ||
| Line 100: | Line 107: | ||
where <math>r</math> denotes the strength of the input pump light, and for | where <math>r</math> denotes the strength of the input pump light, and for | ||
simplicity, we fix <math>\phi</math> in the following. | simplicity, we fix <math>\phi</math> in the following. | ||
| + | |||
Motivated by this Hamiltonian for the optical parametric oscillator, | Motivated by this Hamiltonian for the optical parametric oscillator, | ||
we may define a mathematical operator which produces squeezed states: | we may define a mathematical operator which produces squeezed states: | ||
| Line 109: | Line 117: | ||
Note that the operator in the exponent has the form <math>iA</math>, where <math>A</math> is | Note that the operator in the exponent has the form <math>iA</math>, where <math>A</math> is | ||
Hermitian, so <math>S(r) = \exp[iA]</math> is manifestly a unitary transform. | Hermitian, so <math>S(r) = \exp[iA]</math> is manifestly a unitary transform. | ||
| + | |||
What does <math>S(r)</math> do? A useful mathematical technique for dealing with | What does <math>S(r)</math> do? A useful mathematical technique for dealing with | ||
<math>S(r)</math> is to understand how it transforms operators in the Heisenberg | <math>S(r)</math> is to understand how it transforms operators in the Heisenberg | ||
| Line 120: | Line 129: | ||
Let us use | Let us use | ||
:<math> | :<math> | ||
| − | x = \frac{a+ a^\dagger }{2} ~~~~~~~ p = \frac{a- a^\dagger }{\sqrt{ | + | x = \frac{a+ a^\dagger }{\sqrt{2}} ~~~~~~~ p = \frac{a- a^\dagger }{\sqrt{2}i} |
\,, | \,, | ||
</math> | </math> | ||
| Line 132: | Line 141: | ||
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| − | This shows that <math>S(r)</math> squeezes noise from the | + | |
| − | noise to the | + | This shows that <math>S(r)</math> squeezes noise from the momentum and adds |
| + | noise to the position of a harmonic oscillator state. Consider, for | ||
example, the effect of this operator on the vauum state, <math>S(r)|0{\rangle}</math>, | example, the effect of this operator on the vauum state, <math>S(r)|0{\rangle}</math>, | ||
which we call the "squeezed vacuum" state. The <math>Q(\alpha)</math> plot of | which we call the "squeezed vacuum" state. The <math>Q(\alpha)</math> plot of | ||
| Line 141: | Line 151: | ||
Note that since <math>S(r)</math> is unitary, it leaves <math>\Delta x\,\Delta p</math> | Note that since <math>S(r)</math> is unitary, it leaves <math>\Delta x\,\Delta p</math> | ||
invariant, so <math>S(r)|0{\rangle}</math> is a minumim uncertainty state, since <math>|0{\rangle}</math> is. | invariant, so <math>S(r)|0{\rangle}</math> is a minumim uncertainty state, since <math>|0{\rangle}</math> is. | ||
| + | |||
We can explicitly compute what <math>S(r)|0{\rangle}</math> is as follows: | We can explicitly compute what <math>S(r)|0{\rangle}</math> is as follows: | ||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
| Line 152: | Line 163: | ||
Note that this state only has nonzero probability amplitude to have an | Note that this state only has nonzero probability amplitude to have an | ||
even number of photons! | even number of photons! | ||
| + | |||
| + | ==== Coherent state representation of squeezed states ==== | ||
| + | |||
Another usful representation for the squeezed vacuum is in terms of | Another usful representation for the squeezed vacuum is in terms of | ||
| − | coherent states: | + | coherent states<ref>[http://prola.aps.org/abstract/PRA/v64/i3/e034302 Janszky, Koniorczyk, and Gabris, PRA 64, 034302, 2001]</ref>: |
:<math> | :<math> | ||
S(r)|0 \rangle = \frac{1}{\sqrt{\pi}} \frac{e^{r/2}}{\sqrt{e^{2r}-1}} | S(r)|0 \rangle = \frac{1}{\sqrt{\pi}} \frac{e^{r/2}}{\sqrt{e^{2r}-1}} | ||
| Line 181: | Line 195: | ||
::[[Image:chapter2-quantum-light-part-2-lect5-position-estate.png|thumb|204px|none|]] | ::[[Image:chapter2-quantum-light-part-2-lect5-position-estate.png|thumb|204px|none|]] | ||
::[[Image:chapter2-quantum-light-part-2-lect5-momentum-estate.png|thumb|204px|none|]] | ::[[Image:chapter2-quantum-light-part-2-lect5-momentum-estate.png|thumb|204px|none|]] | ||
| + | |||
| + | ==== The Displacement Operator ==== | ||
| + | |||
How can squeezing produce finite valued position and momentum | How can squeezing produce finite valued position and momentum | ||
eigenstates? Physically, a simple harmonic oscillator such as an | eigenstates? Physically, a simple harmonic oscillator such as an | ||
| Line 186: | Line 203: | ||
displacing the pendulum, and the same is done to produce squeezed | displacing the pendulum, and the same is done to produce squeezed | ||
states of <math> \langle p{\rangle}\neq 0</math> and <math> \langle q{\rangle}\neq 0</math>. | states of <math> \langle p{\rangle}\neq 0</math> and <math> \langle q{\rangle}\neq 0</math>. | ||
| + | |||
We define the mathematical displacement operator <math>D(\alpha)</math> as | We define the mathematical displacement operator <math>D(\alpha)</math> as | ||
:<math> | :<math> | ||
| Line 208: | Line 226: | ||
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
| + | |||
Since <math> D(\alpha) |0{\rangle}</math> is thus an eigenstate of <math>a</math>, it must be the case | Since <math> D(\alpha) |0{\rangle}</math> is thus an eigenstate of <math>a</math>, it must be the case | ||
that <math> D(\alpha) |0 \rangle = |\alpha{\rangle}</math>. The displacement operator displaces | that <math> D(\alpha) |0 \rangle = |\alpha{\rangle}</math>. The displacement operator displaces | ||
| Line 214: | Line 233: | ||
Using the displacement operator, squeezed states with finite momentum | Using the displacement operator, squeezed states with finite momentum | ||
and position can thus be described, for example, by | and position can thus be described, for example, by | ||
| − | <math>D(\alpha)S(r)|0{\rangle}</math>. What do these states look like, both in the | + | <math>D(\alpha)S(r)|0{\rangle}</math>. |
| + | |||
| + | ==== Electric Field of Squeezed States ==== | ||
| + | |||
| + | What do these states look like, both in the | ||
<math>Q(\alpha)</math> representation, as well as their electric field? Recall | <math>Q(\alpha)</math> representation, as well as their electric field? Recall | ||
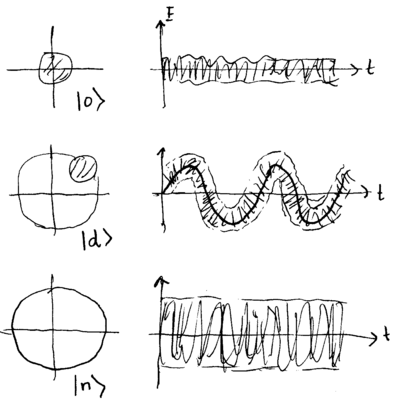
that the vacuum, coherent state, and number states look as follows: | that the vacuum, coherent state, and number states look as follows: | ||
| Line 226: | Line 249: | ||
shall see later, this reduced noise level can be used to improve the | shall see later, this reduced noise level can be used to improve the | ||
precision of certain measurements. | precision of certain measurements. | ||
| + | |||
=== Homodyne detection === | === Homodyne detection === | ||
How can we experimentally detect if a state is squeezed? Ideally, | How can we experimentally detect if a state is squeezed? Ideally, | ||
| Line 254: | Line 278: | ||
a_0 &=& U_{bs} a U_{bs}^\dagger = \frac{a+b}{\sqrt{2}} | a_0 &=& U_{bs} a U_{bs}^\dagger = \frac{a+b}{\sqrt{2}} | ||
\\ | \\ | ||
| − | + | b_0 &=& U_{bs} b U_{bs}^\dagger = \frac{a-b}{\sqrt{2}} | |
| + | \,. | ||
| + | \end{array}</math> | ||
| + | Note that we have adopted a convention which does away with imaginary | ||
| + | phases, for convenience; in the literature, you may find different | ||
| + | convention used, to reflect phases imparted by actual half-silvered | ||
| + | mirror beamsplitters used in the laboratory. | ||
| + | The detected signal <math>I_-</math> thus results from | ||
| + | :<math> | ||
| + | I_- = a^\dagger _0 a_0 - b^\dagger _0 b_0 = a b^\dagger + a^\dagger b | ||
| + | \,. | ||
| + | </math> | ||
| + | If mode <math>b</math> has a strong coherent state <math>|\beta{\rangle}</math> as input, with | ||
| + | <math>\beta = |\beta|e^{i\theta}</math>, then we may write as a normalized output | ||
| + | signal, | ||
| + | :<math>\begin{array}{rcl} | ||
| + | X_\theta &=& \frac{I_-}{2|\beta|} | ||
| + | \\ | ||
| + | &=& \frac{a\beta^* + a^\dagger \beta}{2|\beta|} | ||
| + | \\ | ||
| + | &=& \frac{a e^{-i\theta} + a^\dagger e^{i\theta}}{2} | ||
| + | \,. | ||
| + | \end{array}</math> | ||
| + | Two important values of this signal are | ||
| + | :<math>\begin{array}{rcl} | ||
| + | \mbox{for} ~~ \theta=0 ~~&:&~~ X_\theta = \frac{a+ a^\dagger }{2} = x | ||
| + | \\ | ||
| + | ~~~~~ \theta=\frac{\pi}{2} ~~&:&~~ X_\theta = \frac{a- a^\dagger }{2i} = p | ||
| + | \,. | ||
| + | \end{array}</math> | ||
| + | This thus shows how a beamsplitter and a strong coherent state input | ||
| + | source can be used to experimentally measure <math>x</math> and <math>p</math> quadratures | ||
| + | of a light field. | ||
| + | The technique just described uses a 50/50 beamsplitter, and is known | ||
| + | as "balanced homodyne" detection. | ||
| + | A similar technique, using an unblanced beamsplitter, say one with | ||
| + | <math>99\%</math> transmission of the <math>a</math> mode, is known as "unbalanced | ||
| + | homodyne" mixing, and useful for a different purpose. Consider this setup: | ||
| + | ::[[Image:chapter2-quantum-light-part-2-lect5-unbal-hom.png|thumb|204px|none|]] | ||
| + | The output port operator for <math>a_0</math> may be expressed as | ||
| + | :<math> | ||
| + | a_0 = T a - \sqrt{1-T^2} b | ||
| + | \,. | ||
| + | </math> | ||
| + | Now let a strong coherent state <math>|\beta{\rangle}</math> be input to port <math>b</math>, such | ||
| + | that to good approximation, in the limit that <math>T\approx 1</math>, we may write | ||
| + | :<math>\begin{array}{rcl} | ||
| + | a_0 &\approx& T a - \sqrt{1-T^2} \beta | ||
| + | \\ | ||
| + | &\approx& T ( a - \sqrt{1-T^2} \beta ) | ||
| + | \\ | ||
| + | &\approx& D(\sqrt{1-T^2} \beta ) a D(\sqrt{1-T^2} \beta )^\dagger | ||
| + | \,. | ||
| + | \end{array}</math> | ||
| + | Unbalanced homodyne mixing thus allows approximation experimental | ||
| + | implementation of a displacement operation. | ||
| + | |||
| + | === Teleportation of light === | ||
| + | We conclude this section with an exploration of an exotic application | ||
| + | of squeezed states: the teleportation of a quantum state of light. In | ||
| + | order to clearly convey the basic concepts, this treatment will | ||
| + | emphasize empirical understanding, above mathematical rigor. | ||
| + | So far, we have limited ourselves to studying a single mode of light. | ||
| + | It is not hard to see, however, that two-mode squeezed states are also | ||
| + | possible, and that for example, straightforward generalization of the | ||
| + | squeezing operator <math>S(r)</math> from Eq.(\ref{eq:c2-sdef}) to two modes gives | ||
| + | :<math> | ||
| + | \exp \left[ { -\frac{r}{2}(a_1a_2 - a^\dagger _1 a^\dagger _2) } \right] |0 \rangle _1|0 \rangle _2 | ||
| + | \propto \frac{1}{\cosh r}\sum_n \tanh^n r |n \rangle _1|n \rangle _2 | ||
| + | \,. | ||
| + | </math> | ||
| + | This state can also be expressed as a superposition of coherent | ||
| + | states, of the form | ||
| + | :<math> | ||
| + | \int d\alpha\; |\alpha{\rangle}|\alpha{\rangle} | ||
| + | \,, | ||
| + | </math> | ||
| + | and given that momentum and position eigenstates can be expressed as | ||
| + | infinite superpositions of coherent states, as in | ||
| + | Eqs.(\ref{eq:c2-mstate}-\ref{eq:c2-pstate}), it is reasonable to believe | ||
| + | that such an infinitely-squeezed two-mode state could be expressed (in | ||
| + | unnormalized form) as | ||
| + | :<math> | ||
| + | \int dx\; |x{\rangle}|x{\rangle} | ||
| + | \,, | ||
| + | </math> | ||
| + | where <math>|x{\rangle}</math> represents a position basis state. | ||
| + | |||
| + | Let us begin with such an infinitely-squeezed two-mode state, and show | ||
| + | how a state of light can be teleported. In the following, state | ||
| + | vectors <math>|x \rangle _k</math> and <math>|y \rangle _k</math> will denote position basis states, | ||
| + | <math>|p \rangle _k</math> will denote a momentum basis state, and the subscript <math>k</math> | ||
| + | will deliniate the mode. Three modes will be involved. Overall | ||
| + | normalization factors will be neglected. | ||
| + | |||
| + | [[Entangled Photons Applications - Experimental Realization of Teleportation|The setup is as follows]]: | ||
| + | ::[[Image:chapter2-quantum-light-part-2-lect5-teleportation.png|thumb|600px|none|]] | ||
| + | where the initial state begins at the top of the diagram, and time | ||
| + | evolves downward. Modes <math>2</math> and <math>3</math> contain the squeezed state, and | ||
| + | an unknown quantum state | ||
| + | :<math> | ||
| + | |\psi \rangle = \int dx\; f(x) |x \rangle _1 | ||
| + | </math> | ||
| + | is input. The main idea is that modes <math>1</math> and <math>2</math> belong to one | ||
| + | person (call her "Alice"), and mode <math>3</math> belongs to another person | ||
| + | ("Bob"). Alice and Bob jointly share the two-mode squeezed state, | ||
| + | which was distributed to them long before <math>|\psi{\rangle}</math> came into | ||
| + | existence. Only Alice has <math>|\psi{\rangle}</math>, and she would like to | ||
| + | communicate it to Bob, but the quantum link is down, and all she can | ||
| + | do is to mail him a classical message. Normally, this would be | ||
| + | impossible, but, because they have the pre-shared two-mode squeezed | ||
| + | state, they can use it to communicate <math>|\psi{\rangle}</math>, following this procedure. | ||
| + | |||
| + | The initial state of the three modes is | ||
| + | :<math> | ||
| + | |\phi_0 \rangle = \int\int dx\; dy\; f(x) |x \rangle _1 |y \rangle _2 |y \rangle _3 | ||
| + | \,. | ||
| + | </math> | ||
| + | The first two modes are now sent through a beamsplitter, resulting in | ||
| + | :<math> | ||
| + | |\phi_1 \rangle = \int\int dx\; dy\; f(x) | ||
| + | \left | \frac{x-y}{\sqrt{2}} \right \rangle _1 | ||
| + | \left | \frac{x+y}{\sqrt{2}} \right \rangle _2 | ||
| + | |y \rangle _3 | ||
| + | \,. | ||
| + | </math> | ||
| + | Recall that position eigenstates may be expressed as weighted sums | ||
| + | over momentum eigenstates, as | ||
| + | :<math> | ||
| + | |x \rangle = \int dp\; e^{ixp} |p{\rangle} | ||
| + | \,, | ||
| + | </math> | ||
| + | so that <math>|\phi_1{\rangle}</math> may be equivalently expressed as | ||
| + | :<math> | ||
| + | |\phi_1 \rangle = \int\int\int dx\; dy\; dp\; f(x) | ||
| + | e^{i(x+y)p/\sqrt{2}} | ||
| + | \left | \frac{x-y}{\sqrt{2}} \right \rangle _1 | ||
| + | \left | p \right \rangle _2 | ||
| + | |y \rangle _3 | ||
| + | \,. | ||
| + | </math> | ||
| + | Alice now measures the photons in her two modes; she performs a | ||
| + | homodyne <math>x</math>-measurement of mode <math>1</math>, and a <math>p</math>-measurement of mode | ||
| + | <math>2</math>. Let <math>x_1</math> and <math>p_2</math> be her measurement results. Therefore, | ||
| + | <math>x_1=(x-y)/\sqrt{2}</math> and <math>x=\sqrt{2} x_1 + y </math>. The | ||
| + | post-measurement state <math>|\phi_2{\rangle}</math> is | ||
| + | :<math> | ||
| + | |\phi_2 \rangle = e^{ix_1 p_2} \int dy\; f(y+\sqrt{2}x_1) | ||
| + | e^{i 2yp_2/\sqrt{2}} | ||
| + | |y \rangle _3 | ||
| + | \,. | ||
| + | </math> | ||
| + | Changing variables from <math>y</math> to <math>z = y+\sqrt{2}x_1</math>, this becomes | ||
| + | :<math> | ||
| + | |\phi_2 \rangle = e^{ix_1 p_2} \int dz\; f(z) | ||
| + | e^{i(z-\sqrt{2}x_1)\sqrt{2} p_2} | ||
| + | |z-\sqrt{2}x_1 \rangle _3 | ||
| + | \,, | ||
| + | </math> | ||
| + | which is just a displaced version of the original state, up to an | ||
| + | irrelevant overall phase: | ||
| + | :<math>\begin{array}{rcl} | ||
| + | |\phi_2 \rangle &=& e^{ix_1p_2} \int dz\; f(z) D(\sqrt{2}(x_1 + | ||
| + | i p_2) |z{\rangle} | ||
| + | \\ | ||
| + | &=& e^{ix_1p_2} D(\sqrt{2}(x_1 +i p_2) |\psi{\rangle} | ||
| + | \,. | ||
| + | \end{array}</math> | ||
| + | Thus, if Alice sends Bob her measurement results <math>x_1</math> and <math>p_1</math>, then | ||
| + | he can reconstruct <math>|\psi{\rangle}</math> by applying the displacement | ||
| + | <math>D(\sqrt{2}(x_1 + i p_2)</math> using an unbalanced homodyne operation. | ||
| + | |||
| + | The elegance of this version of quantum teleportation is in its | ||
| + | experimental implementation: given the two-mode squeezed state, | ||
| + | everything else in the protocol is experimentally straightforward. | ||
| + | Indeed, this is why the above procedure has been experimentally | ||
| + | implemented. [[Entangled Photons Applications - Experimental Realization of Teleportation|Go read about it]]: [http://www.scienceonline.org/cgi/content/short/282/5389/706 Furusawa et al, Science vol. 282, p.706, 1998]; also see the [http://www.sciencemag.org/cgi/content/abstract/323/5913/486 recent teleportation of matter qubits, done between two Yb ions]. | ||
| + | |||
| + | === References === | ||
| + | |||
| + | <references/> | ||
| + | |||
| + | * <refbase>5233</refbase> | ||
| + | * <refbase>5234</refbase> | ||
| + | * <refbase>5235</refbase> | ||
| + | |||
| + | [[Category:Quantum Light|2]] | ||
Latest revision as of 20:38, 31 January 2017
One of the most special properties of the coherent state is that its fluctuations in and are equal, and minimal, meaning that it satisfies the Heisenberg limit . However, satisfying this limit does not require equal noise in the two conjugate variables; it is certainly permissible for noise in one to be larger than the other. Such states can, in principle, be quite useful, for example, if a measurement only involves , and excess noise in can be disregarded. In this section, we define such squeezed states, and explore their physical properties. We begin with classical squeezing, then define squeezed states of a quantum simple harmonic oscillator, describe how squeezing can be experimentally detected, then show how it can be useful in a quantum experiment: teleportation.
Contents
Classical squeezing
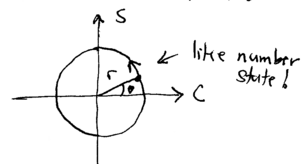
We are interested in the dynamics of the simple harmonic oscillator, and it is useful to obtain some intuition about what is possible from considering the classical oscillator. Consider a particle in the potential The equations of motion for this particle, have the solution
where , , and are constant. This motion is circular:
Suppose a small, "parametric" driving force is added, analogous to kicking while on a swing. For a swinging pendulum, this force could be applied by tugging gently up and down on the string as the pendulum oscillates back and forth. Let this force be applied at twice the frequency of the natural harmonic motion, such that the potential becomes
where is small.

Substituting the above ansatz for into the equation of motion
approximating , and averaging away terms rapidly oscillating at , we obtain new approximate equations of motion
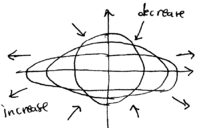
with solutions
This shows that the circular motion in phase space evolves under the parametric drive to become elliptical:
What is the ultimate limit of this classical squeezing effect? The answer turns out to be quantum noise, which enforces the Heisenberg uncertainty limit, .
Squeezed states: quantum
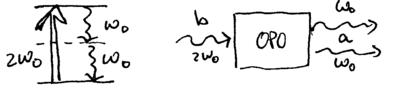
A quantum simple harmonic oscillator excited by a parametric drive at will also generate squeezed states. Physically, such a process corresponds to a "nonlinear" interaction which involves photons interacting with each other, via the medium they are transported through or generated from. One important physical process that generates squeezed states of light is known as the optical parametric oscillator, which we may think of as being an atomic system that is driven at , and produces two photons at and , due to cascaded decay from two equaly spaced energy levels:
Such a process can be described by the Hamiltonian
where acts on the output mode at frequency , and the input mode, at frequency . If the input light is a strong coherent field, then to a good approximation, we may replace and by a classical variable in this Hamiltonian, obtaining
where denotes the strength of the input pump light, and for simplicity, we fix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} in the following.
Motivated by this Hamiltonian for the optical parametric oscillator, we may define a mathematical operator which produces squeezed states:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(r) = \exp \left[ { -\frac{r}{2}(a^2 - { a^\dagger }^2) } \right] \,. }
Note that the operator in the exponent has the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle iA} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is Hermitian, so Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(r) = \exp[iA]} is manifestly a unitary transform.
What does Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(r)} do? A useful mathematical technique for dealing with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(r)} is to understand how it transforms operators in the Heisenberg picture. For example,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} S(r) x S(r)^\dagger &=& e^{iA} x e^{-iA} \\ &=& x + [iA,x] + \frac{[iA,[iA,x]]}{2!} + \cdots \,, \end{array}}
Let us use
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = \frac{a+ a^\dagger }{\sqrt{2}} ~~~~~~~ p = \frac{a- a^\dagger }{\sqrt{2}i} \,, }
as dimensionless Hermitean operators for position and momentum. Under the squeezing operator, using the above expansion, it is straightforward to show that position and momentum transform to become:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} S(r) x S(r)^\dagger &=& x e^r \\ S(r) p S(r)^\dagger &=& p e^{-r} \,. \end{array}}
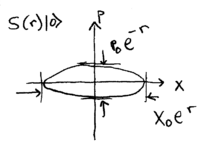
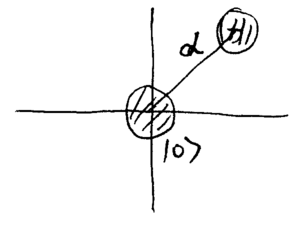
This shows that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(r)} squeezes noise from the momentum and adds noise to the position of a harmonic oscillator state. Consider, for example, the effect of this operator on the vauum state, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(r)|0{\rangle}} , which we call the "squeezed vacuum" state. The Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q(\alpha)} plot of this squeezed vacuum is:
\noindent Note that since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(r)} is unitary, it leaves Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x\,\Delta p} invariant, so is a minumim uncertainty state, since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0{\rangle}} is.
We can explicitly compute what is as follows:
Note that this state only has nonzero probability amplitude to have an even number of photons!
Coherent state representation of squeezed states
Another usful representation for the squeezed vacuum is in terms of coherent states[1]:
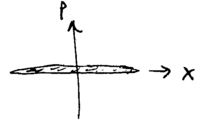
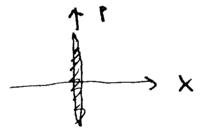
This representation allows us to depict useful limits, such as when , the inifinite squeezing limit, giving a state we may call :
and similarly, we may define
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |x=0{\rangle} \propto \int_{-\infty}^\infty d\alpha\; |i\alpha{\rangle} \,. }
These two states have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q(\alpha)} plots which are of infinite extent, horizontally (for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} ) and vertically (for ), indicating that infinitely squeezed states are position and momentum eigenstates:
The Displacement Operator
How can squeezing produce finite valued position and momentum eigenstates? Physically, a simple harmonic oscillator such as an oscillating pendulum is given a finite momentum or position by displacing the pendulum, and the same is done to produce squeezed states of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle p{\rangle}\neq 0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle q{\rangle}\neq 0} .
We define the mathematical displacement operator Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(\alpha)} as
It is straightforward to show (by expanding the exponential, for example), that this operator has the property that
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} D(\alpha)a D(\alpha)^\dagger &=& a-\alpha \\ D(\alpha)^\dagger a D(\alpha) &=& a+\alpha \,, \end{array}}
such that the displaced vacuum state satisfies
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} a D(\alpha)|0 \rangle &=& D(\alpha) D(\alpha) ^\dagger a D(\alpha) |0{\rangle} \\ &=& D(\alpha) (a+\alpha) |0{\rangle} \\ &=& \alpha D(\alpha) |0{\rangle} \,. \end{array}}
Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(\alpha) |0{\rangle}} is thus an eigenstate of , it must be the case that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(\alpha) |0 \rangle = |\alpha{\rangle}} . The displacement operator displaces the vacuum state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0{\rangle}} to become a coherent state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha{\rangle}} :
Using the displacement operator, squeezed states with finite momentum and position can thus be described, for example, by .
Electric Field of Squeezed States
What do these states look like, both in the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q(\alpha)} representation, as well as their electric field? Recall that the vacuum, coherent state, and number states look as follows:
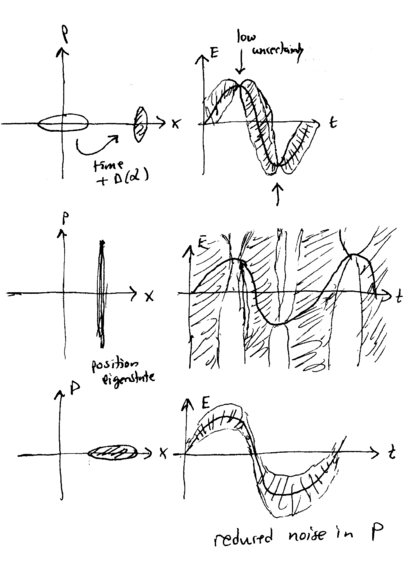
A displaced, partially squeezed state, a near-position eigenstate, and a near-momentum eigenstate correspondingly look like this:
Note how the squeezed states attain electric fields which are, at times, very low in either amplitude or phase uncertainty. By employing these states in the right kind of interferometer, as we shall see later, this reduced noise level can be used to improve the precision of certain measurements.
Homodyne detection
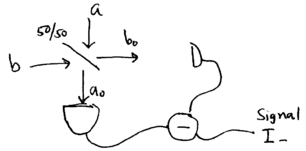
How can we experimentally detect if a state is squeezed? Ideally, squeezing could be detected by measuring the noise level in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} . However, photodetectors are square-law detectors which sense light intensity, meaning photon number, and not quadrature field components. Nevertheless, the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} field components can be detected if the input light is first transformed by beating it with a reference signal of fixed phase. Intuitively, this follows the principle upon which many early radios worked: by mixing a signal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(t) = c(t) \cos \omega_0 t + s(t) \sin\omega_0 t} with a reference oscillator , the cosine and sine components Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c(t)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s(t)} can be picked out. This method is known as homodyne detection, because it involves mixing with a reference at the same frequency as the signal. With radio frequency signals, a diode is used to mix signal and reference; the nonlinearity of the diode produces an output which is to first order, the product of the signal and reference. Mixing of light frequency signals is done with a beamsplitter. Consider a 50/50 beamsplitter with the signal input into port Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} , and the reference into port , and detectors placed at the two outputs:
The beamsplitter mixes the two input ports, performing a unitary transform Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{bs}} that relates the output port operators Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_0} to the input port operators and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} ,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} a_0 &=& U_{bs} a U_{bs}^\dagger = \frac{a+b}{\sqrt{2}} \\ b_0 &=& U_{bs} b U_{bs}^\dagger = \frac{a-b}{\sqrt{2}} \,. \end{array}}
Note that we have adopted a convention which does away with imaginary phases, for convenience; in the literature, you may find different convention used, to reflect phases imparted by actual half-silvered mirror beamsplitters used in the laboratory. The detected signal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_-} thus results from
If mode Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} has a strong coherent state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\beta{\rangle}} as input, with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = |\beta|e^{i\theta}} , then we may write as a normalized output signal,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} X_\theta &=& \frac{I_-}{2|\beta|} \\ &=& \frac{a\beta^* + a^\dagger \beta}{2|\beta|} \\ &=& \frac{a e^{-i\theta} + a^\dagger e^{i\theta}}{2} \,. \end{array}}
Two important values of this signal are
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \mbox{for} ~~ \theta=0 ~~&:&~~ X_\theta = \frac{a+ a^\dagger }{2} = x \\ ~~~~~ \theta=\frac{\pi}{2} ~~&:&~~ X_\theta = \frac{a- a^\dagger }{2i} = p \,. \end{array}}
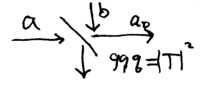
This thus shows how a beamsplitter and a strong coherent state input source can be used to experimentally measure and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} quadratures of a light field. The technique just described uses a 50/50 beamsplitter, and is known as "balanced homodyne" detection. A similar technique, using an unblanced beamsplitter, say one with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 99\%} transmission of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} mode, is known as "unbalanced homodyne" mixing, and useful for a different purpose. Consider this setup:
The output port operator for may be expressed as
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0 = T a - \sqrt{1-T^2} b \,. }
Now let a strong coherent state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\beta{\rangle}} be input to port , such that to good approximation, in the limit that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\approx 1} , we may write
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} a_0 &\approx& T a - \sqrt{1-T^2} \beta \\ &\approx& T ( a - \sqrt{1-T^2} \beta ) \\ &\approx& D(\sqrt{1-T^2} \beta ) a D(\sqrt{1-T^2} \beta )^\dagger \,. \end{array}}
Unbalanced homodyne mixing thus allows approximation experimental implementation of a displacement operation.
Teleportation of light
We conclude this section with an exploration of an exotic application of squeezed states: the teleportation of a quantum state of light. In order to clearly convey the basic concepts, this treatment will emphasize empirical understanding, above mathematical rigor. So far, we have limited ourselves to studying a single mode of light. It is not hard to see, however, that two-mode squeezed states are also possible, and that for example, straightforward generalization of the squeezing operator Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(r)} from Eq.(\ref{eq:c2-sdef}) to two modes gives
This state can also be expressed as a superposition of coherent states, of the form
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\alpha\; |\alpha{\rangle}|\alpha{\rangle} \,, }
and given that momentum and position eigenstates can be expressed as infinite superpositions of coherent states, as in Eqs.(\ref{eq:c2-mstate}-\ref{eq:c2-pstate}), it is reasonable to believe that such an infinitely-squeezed two-mode state could be expressed (in unnormalized form) as
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int dx\; |x{\rangle}|x{\rangle} \,, }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |x{\rangle}} represents a position basis state.
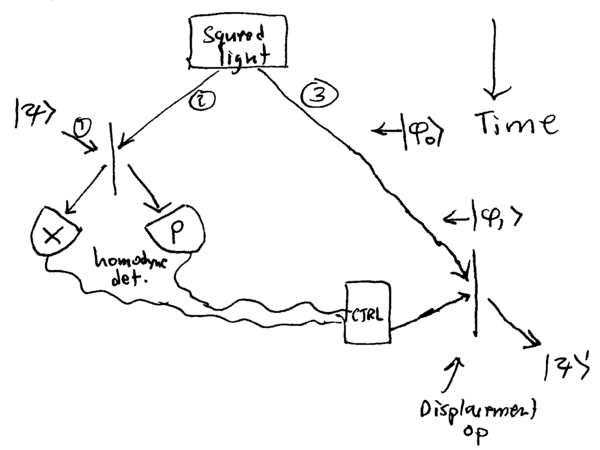
Let us begin with such an infinitely-squeezed two-mode state, and show how a state of light can be teleported. In the following, state vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |x \rangle _k} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |y \rangle _k} will denote position basis states, will denote a momentum basis state, and the subscript Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} will deliniate the mode. Three modes will be involved. Overall normalization factors will be neglected.
where the initial state begins at the top of the diagram, and time evolves downward. Modes and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3} contain the squeezed state, and an unknown quantum state
is input. The main idea is that modes Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2} belong to one person (call her "Alice"), and mode Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3} belongs to another person ("Bob"). Alice and Bob jointly share the two-mode squeezed state, which was distributed to them long before came into existence. Only Alice has Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi{\rangle}} , and she would like to communicate it to Bob, but the quantum link is down, and all she can do is to mail him a classical message. Normally, this would be impossible, but, because they have the pre-shared two-mode squeezed state, they can use it to communicate , following this procedure.
The initial state of the three modes is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\phi_0 \rangle = \int\int dx\; dy\; f(x) |x \rangle _1 |y \rangle _2 |y \rangle _3 \,. }
The first two modes are now sent through a beamsplitter, resulting in
Recall that position eigenstates may be expressed as weighted sums over momentum eigenstates, as
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |x \rangle = \int dp\; e^{ixp} |p{\rangle} \,, }
so that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\phi_1{\rangle}} may be equivalently expressed as
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\phi_1 \rangle = \int\int\int dx\; dy\; dp\; f(x) e^{i(x+y)p/\sqrt{2}} \left | \frac{x-y}{\sqrt{2}} \right \rangle _1 \left | p \right \rangle _2 |y \rangle _3 \,. }
Alice now measures the photons in her two modes; she performs a homodyne -measurement of mode Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} , and a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} -measurement of mode Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2} . Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1} and be her measurement results. Therefore, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=(x-y)/\sqrt{2}} and . The post-measurement state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\phi_2{\rangle}} is
Changing variables from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = y+\sqrt{2}x_1} , this becomes
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\phi_2 \rangle = e^{ix_1 p_2} \int dz\; f(z) e^{i(z-\sqrt{2}x_1)\sqrt{2} p_2} |z-\sqrt{2}x_1 \rangle _3 \,, }
which is just a displaced version of the original state, up to an irrelevant overall phase:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} |\phi_2 \rangle &=& e^{ix_1p_2} \int dz\; f(z) D(\sqrt{2}(x_1 + i p_2) |z{\rangle} \\ &=& e^{ix_1p_2} D(\sqrt{2}(x_1 +i p_2) |\psi{\rangle} \,. \end{array}}
Thus, if Alice sends Bob her measurement results Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1} , then he can reconstruct Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi{\rangle}} by applying the displacement Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(\sqrt{2}(x_1 + i p_2)} using an unbalanced homodyne operation.
The elegance of this version of quantum teleportation is in its experimental implementation: given the two-mode squeezed state, everything else in the protocol is experimentally straightforward. Indeed, this is why the above procedure has been experimentally implemented. Go read about it: Furusawa et al, Science vol. 282, p.706, 1998; also see the recent teleportation of matter qubits, done between two Yb ions.
References
- <refbase>5233</refbase>
- <refbase>5234</refbase>
- <refbase>5235</refbase>





![{\displaystyle {\begin{array}{rcl}x(t)&=&r(t)\cos \left[{\omega _{0}t-\theta (t)}\right]\\&=&c(t)\cos \omega _{0}t+s(t)\sin \omega _{0}t\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed1126f0314b124b847a7002315b85c3ebe46531)



![{\displaystyle V(x)={\frac {1}{2}}m\omega _{0}^{2}x^{2}\left[{1+\epsilon \sin 2\omega _{0}t}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edff86a2e3d12726d0213449d5ae7228eefca2d0)


![{\displaystyle {\ddot {x}}=-\omega _{0}^{2}\left[{1+\epsilon \sin 2\omega _{0}t}\right]x(t)\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1e3676b6d9d447947628c0faa1a8c06be12dca6)














![{\displaystyle {\begin{array}{rcl}S(r)|0\rangle &=&\sum _{k=0}^{\infty }{\frac {1}{k!}}\left[{-{\frac {r}{2}}(a^{2}-{a^{\dagger }}^{2})}\right]^{k}|0{\rangle }\\&=&{\frac {1}{\sqrt {\cosh r}}}\sum _{n=0}^{\infty }{\frac {\sqrt {(2n)!}}{2^{n}n!}}(\tanh r)^{n}|2n{\rangle }\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ddf7dcb3b019cbc045a92cdab3abbc501b1ad3f)





![{\displaystyle D(\alpha )=\exp \left[{\alpha a^{\dagger }-\alpha ^{*}a}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b380dce7a8eb51fea894d41eddb7f38170b2b89c)




![{\displaystyle \exp \left[{-{\frac {r}{2}}(a_{1}a_{2}-a_{1}^{\dagger }a_{2}^{\dagger })}\right]|0\rangle _{1}|0\rangle _{2}\propto {\frac {1}{\cosh r}}\sum _{n}\tanh ^{n}r|n\rangle _{1}|n\rangle _{2}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6bf1af8494ef225a35d9b5c9aa9daa68bbf300a)