Difference between revisions of "Effects of the Nucleus on Atomic Structure"
imported>Ketterle |
m (→Hyperfine structure at zero magnetic field: Corrected formula for s state atom hyperfine splitting) |
||
| (26 intermediate revisions by 9 users not shown) | |||
| Line 48: | Line 48: | ||
electrons affect the magnetic and electric interactions of the | electrons affect the magnetic and electric interactions of the | ||
valence electrons with the nucleus. | valence electrons with the nucleus. | ||
| + | |||
| + | ==Allowable Multipole Moments in Nuclei== | ||
| + | |||
| + | ===Introduction=== | ||
| + | In general, nuclei are composed of more than one particles, and hence it is possible for nuclei to have multipole moments beyond electric monopole and magnetic dipole. Multipole moments of a nucleus arise from its angular momentum <math>I</math>, and the allowed moments are governed by both <math>I</math> and symmetry consideration. In this section, we discuss what are the possible multipole moments for nuclei. We shall denote the order of multipoles as follow: monopole <math>l=0</math>, dipole <math>l=1</math>, quadrupole <math>l=2</math>, octopole <math>l=3</math>, etc. | ||
| + | |||
| + | ===Angular Momentum and Multipole Moments=== | ||
| + | |||
| + | The multipole moment of a nucleus arises from its angular momentum. To see that, intuitively we know that multipole moment is a consequence of shape. In order to distinguish shapes, one needs be able to distinguish orientation, and it is angular momentum that sets orientation. For example, let us consider a magnetic dipole. In order to measure it, one needs to be able to distinguish between up and down direction, which can be accomplished by passing the dipole through a uniform field and observing whether it moves up or down (Stern-Gerlach experiment). | ||
| + | |||
| + | Q: What is the minimum <math>I</math> for dipole moment? | ||
| + | |||
| + | A: As discussed above, in order to oberseve dipole moment, one needs to be able to distinguish up and down. Quantum mechanically, the dipole moment results in two energy levels different from the single energy level of a monopole. This implies one needs to have at least <math>I=1/2</math>. | ||
| + | |||
| + | Q: What is the minimum <math>I</math> for quadrupole moment? | ||
| + | |||
| + | A: Quadrupole moment is basically an ellipse. In order to tell that one has an ellipse, one needs to be able to distinguish not just up and down, but also an orthogonal orientation. It implies three energy levels, and hence <math>I=1</math>. | ||
| + | |||
| + | In general, in order to possess a moment of order <math>l</math>, a nucleus needs to have at least <math>l\leq 2I</math>. | ||
| + | |||
| + | Formally, let us denote the multipole operator as <math>T_{l,m}</math>, where <math>l</math> is the angular momentum quantum number of the multipole, and <math>m</math> is the azimuthal quantum number. In coordinate space, <math>T_{l,m}(r, \theta, \phi)=r^lY_{l,m}(\theta,\phi)</math> is the solid harmonics, with <math>Y_{l,m}</math> the spherical harmonics. The moment of the nucleus is then given by <math>\langle I, m|T_{l,m}|I, m\rangle</math>. Now, we know the component involving azimuthal quantum number decouples from the angular quantum numbers: <math>\langle I, m|T_{l,m}|I, m\rangle=\langle I|T_l|I\rangle\langle m|T_m|m\rangle</math>. Whether the angular component has non-zero value tells us whether the particular moment is forbidden given the <math>I</math>. Specifically, one can pick <math>T_l=Y_{l,0}(\theta)</math>. The angular dependence of the first few <math>m=0</math> spherical harmonics are given here: | ||
| + | |||
| + | :<math> | ||
| + | Y_{0,0}\propto 1 | ||
| + | </math> | ||
| + | :<math> | ||
| + | Y_{1,0}\propto \cos\theta | ||
| + | </math> | ||
| + | :<math> | ||
| + | Y_{2,0}\propto (3\cos^2\theta-1) | ||
| + | </math> | ||
| + | |||
| + | Graphically, one can imagine the "triangle rule". Consider a vector <math>\vec{l}</math>, and asks how can one add <math>\vec{I}</math> to get <math>\vec{l}</math>. It is possible only when <math>|\vec{I}|</math> is at least <math>|\vec{l}|/2</math>. And hence one also obtains the same condition <math>l\leq 2I</math>. | ||
| + | |||
| + | ===Symmetry Consideration=== | ||
| + | Besides angular momentum consideration, parity symmetry further restricts what specific electric and magnetic multipoles are allowed in a nucleus. Let us begin with an example: can a nucleus possesses a permanent electric dipole moment? Assuming an electric dipole moment <math>\vec{d}</math> is possible, let us apply parity transformation on the nucleus. Electric dipole moment has odd parity and thus changes sign. Therefore, a permanent electric dipole moment is forbidden by parity symmetry. On the other hand, a magnetic dipole moment does not change sign under parity transformation and thus is allowed. | ||
| + | |||
| + | In general, the parity of the multipoles is as follow: | ||
| + | |||
| + | <blockquote> | ||
| + | <table border=0> | ||
| + | <tr> | ||
| + | <td>Electric multipole of order <math>l</math>: </td> | ||
| + | <td> <math>(-1)^l</math></td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td> | ||
| + | Magnetic multipole of order <math>l</math>:</td> | ||
| + | <td> <math>(-1)^{l+1}</math></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | </blockquote> | ||
| + | |||
| + | Therefore, we see that even electric multipoles (<math>l=0</math> monopole, <math>l=2</math> quadrupole, ...) and odd magnetic multipoles (<math>l=1</math> dipole, <math>l=3</math> octopoles, ...) are the only allowed multipole moments. | ||
| + | |||
| + | In summary, we see that symmetry consideration allows a nuclues to have even electric multipoles and odd magnetic multipoles. In addition to these restrictions, angular momentum consideration limits the multipole orders to <math>l\leq 2I</math>. | ||
== Hyperfine interaction == | == Hyperfine interaction == | ||
| Line 142: | Line 198: | ||
}) ({ {\bf{J}} } \cdot { {\bf{B}} | }) ({ {\bf{J}} } \cdot { {\bf{B}} | ||
}_J) /J^2</math>, we have | }_J) /J^2</math>, we have | ||
| − | + | <equation id="EQ_cathree" noautocaption> | |
| − | :<math> | + | <span style="float:right; display:block;"><caption>(%i)</caption></span> |
| + | <math> | ||
ah = -\frac{\mu_I}{I} \langle{ \frac{{ {\bf{J}} }\cdot { {\bf{B}} | ah = -\frac{\mu_I}{I} \langle{ \frac{{ {\bf{J}} }\cdot { {\bf{B}} | ||
}_J}{{ {\bf{J}} }^2} }\rangle | }_J}{{ {\bf{J}} }^2} }\rangle | ||
</math> | </math> | ||
| − | The constant <math> | + | </equation> |
| + | The constant <math>ah</math> is called the hyperfine coupling constant. By | ||
convention, it is written in units of frequency. | convention, it is written in units of frequency. | ||
There are two contributions to <math>{ {\bf{B}} | There are two contributions to <math>{ {\bf{B}} | ||
| Line 176: | Line 234: | ||
\cdot { {\bf{\hat{r}}} }){ {\bf{\hat{r}}} }\right]} | \cdot { {\bf{\hat{r}}} }){ {\bf{\hat{r}}} }\right]} | ||
</math> | </math> | ||
| − | + | <equation id="EQ_caseven" noautocaption> | |
| − | :<math> | + | <span style="float:right; display:block;"><caption>(%i)</caption></span> |
| + | <math> | ||
{ {\bf{B}} }_J (0) = - \frac{2\mu_B}{r^3} {\left[ { {\bf{L}} } | { {\bf{B}} }_J (0) = - \frac{2\mu_B}{r^3} {\left[ { {\bf{L}} } | ||
-\frac{g_e}{2} ({ {\bf{S}} } | -\frac{g_e}{2} ({ {\bf{S}} } | ||
| Line 183: | Line 242: | ||
{ {\bf{\hat{r}}} }) \right]}. | { {\bf{\hat{r}}} }) \right]}. | ||
</math> | </math> | ||
| + | </equation> | ||
We need to evaluate | We need to evaluate | ||
:<math> | :<math> | ||
| Line 196: | Line 256: | ||
</math> | </math> | ||
So after all this work, the field turns out to depend only on | So after all this work, the field turns out to depend only on | ||
| − | <math>\ell</math>. From | + | <math>\ell</math>. From <xr id="EQ_cathree"/>, we obtain |
:<math> | :<math> | ||
ah= + \frac{g_e\mu_I\mu_B}{I} \langle{\frac{1}{r^3} }\rangle \frac{\ell ( \ell + | ah= + \frac{g_e\mu_I\mu_B}{I} \langle{\frac{1}{r^3} }\rangle \frac{\ell ( \ell + | ||
| Line 209: | Line 269: | ||
finally obtain | finally obtain | ||
:<math> | :<math> | ||
| − | ah = \frac{g_e\mu_B Z^3 g_I \frac{m_e}{M_p}}{n^3a_0^3} | + | ah = \frac{g_e\mu_B^2 Z^3 g_I \frac{m_e}{M_p}}{n^3a_0^3} |
\frac{1}{(\ell + 1/2 )J (J +1)} | \frac{1}{(\ell + 1/2 )J (J +1)} | ||
</math> | </math> | ||
| Line 260: | Line 320: | ||
{ {\bf{S}} | { {\bf{S}} | ||
} \left| \psi ( 0 )\right| ^2</math>, | } \left| \psi ( 0 )\right| ^2</math>, | ||
| − | + | <equation id="EQ_caeighteen" noautocaption> | |
| − | :<math> | + | <span style="float:right; display:block;"><caption>(%i)</caption></span> |
| + | <math> | ||
{ {\bf{B}} | { {\bf{B}} | ||
| − | } (0) = - \frac{8\pi}{3}g_e | + | } (0) = (2/3) 4\pi { {\bf{M}} |
| + | } (0) =- \frac{8\pi}{3}g_e \mu_B S \left| \Psi (0)\right| ^2 | ||
</math> | </math> | ||
| + | </equation> | ||
This <math>S</math>-state interaction is often | This <math>S</math>-state interaction is often | ||
called the "contact" (in the sense of touch) term. | called the "contact" (in the sense of touch) term. | ||
| − | We can summarize these results by combining | + | We can summarize these results by combining <xr id="EQ_caseven"/> |
| − | and | + | and <xr id="EQ_caeighteen"/> |
taking <math>g_e</math> = 2: | taking <math>g_e</math> = 2: | ||
| − | + | <equation id="EQ_caninteen" noautocaption> | |
| − | :<math> | + | <span style="float:right; display:block;"><caption>(%i)</caption></span> |
| + | <math> | ||
{ {\bf{B}} }(0) = - 2\mu_B {\left[\frac{{ {\bf{L}} }}{r^3} -\frac{{ {\bf{S}} }}{r^3} + \frac{3({ {\bf{S}} }\cdot{ {\bf{\hat{r}}} }) { {\bf{\hat{r}}} }}{r^3} - \frac{8}{3} \pi\delta ({ {\bf{r}} }) { {\bf{S}} }\right]} | { {\bf{B}} }(0) = - 2\mu_B {\left[\frac{{ {\bf{L}} }}{r^3} -\frac{{ {\bf{S}} }}{r^3} + \frac{3({ {\bf{S}} }\cdot{ {\bf{\hat{r}}} }) { {\bf{\hat{r}}} }}{r^3} - \frac{8}{3} \pi\delta ({ {\bf{r}} }) { {\bf{S}} }\right]} | ||
</math> | </math> | ||
| + | </equation> | ||
The first three terms in the bracket average to zero in an | The first three terms in the bracket average to zero in an | ||
<math>S</math>-state; the last term contributes only | <math>S</math>-state; the last term contributes only | ||
| Line 301: | Line 366: | ||
We can write <math> H = H_0 + H_\text{hf} </math>, where, neglecting the term | We can write <math> H = H_0 + H_\text{hf} </math>, where, neglecting the term | ||
in <math> A_I^2 </math> | in <math> A_I^2 </math> | ||
| − | + | <equation id="EQ_qmt3" noautocaption> | |
| − | :<math> | + | <span style="float:right; display:block;"><caption>(%i)</caption></span> |
| + | <math> | ||
H_\text{hf} = \frac{e}{2m} ({ {\bf{p}} | H_\text{hf} = \frac{e}{2m} ({ {\bf{p}} | ||
}\cdot { {\bf{A}} | }\cdot { {\bf{A}} | ||
| Line 312: | Line 378: | ||
}_I) | }_I) | ||
</math> | </math> | ||
| + | </equation> | ||
We can take <math> { {\bf{A}} | We can take <math> { {\bf{A}} | ||
}_I </math> to obey the Coulomb gauge <math> \nabla\cdot | }_I </math> to obey the Coulomb gauge <math> \nabla\cdot | ||
{ {\bf{A}} | { {\bf{A}} | ||
| − | }_I = 0</math>. Then the first term in Eq. | + | }_I = 0</math>. Then the first term in Eq. <xr id="EQ_qmt3"/> gives |
:<math> | :<math> | ||
{ {\bf{p}} | { {\bf{p}} | ||
| Line 339: | Line 406: | ||
\times \nabla \frac{1}{r}\right]} | \times \nabla \frac{1}{r}\right]} | ||
</math> | </math> | ||
| − | Using this result, the second term in Eq. | + | Using this result, the second term in Eq. <xr id="EQ_qmt3"/> can be |
written | written | ||
:<math> | :<math> | ||
| Line 397: | Line 464: | ||
} +3 ({ {\bf{S}} | } +3 ({ {\bf{S}} | ||
}\cdot | }\cdot | ||
| − | { {\bf{\hat{r}}} }) | + | { {\bf{\hat{r}}} }) { {\bf{\hat{r}}}) } -\frac{8\pi}{3} { {\bf{S}} |
}\delta ({ {\bf{r}} })\right]} | }\delta ({ {\bf{r}} })\right]} | ||
</math> | </math> | ||
| Line 403: | Line 470: | ||
}\cdot { {\bf{J}} | }\cdot { {\bf{J}} | ||
}</math>, we obtain the result | }</math>, we obtain the result | ||
| − | found by the classical argument, Eq. | + | found by the classical argument, Eq. <xr id="EQ_caninteen"/>. |
=== Hyperfine structure at zero magnetic field === | === Hyperfine structure at zero magnetic field === | ||
| Line 454: | Line 521: | ||
:<math> | :<math> | ||
| − | W(F) - W(F-1) = | + | W(F) - W(F-1) = ahF |
</math> | </math> | ||
This result, known as the Lande Interval Rule, played an | This result, known as the Lande Interval Rule, played an | ||
| Line 469: | Line 536: | ||
:<math> | :<math> | ||
| − | ah = | + | ah = \frac{16 \pi}{3} g_I \mu_N \mu_B \left| \Psi (0)\right| ^2 |
</math> | </math> | ||
| + | |||
| + | For hydrogen in the 1s ground state, ah=1420 MHz. The hyperfine interaction splits the <math>1 ^2S_{1/2}</math> ground state into an F=1 component (shifted up by ah/4) and an F=0 component (shifted down by 3 ah/4). | ||
=== Electric quadrupole interaction === | === Electric quadrupole interaction === | ||
| Line 484: | Line 553: | ||
deformations of the nucleus. Some nuclei are observed with 30 % | deformations of the nucleus. Some nuclei are observed with 30 % | ||
differences between polar and equatorial axes, so <math>Q</math> can be | differences between polar and equatorial axes, so <math>Q</math> can be | ||
| − | comparable to <math> \left\langle r^2\right\rangle </math> , i.e.~<math> | + | comparable to <math> \left\langle r^2\right\rangle </math> , i.e.~<math> {\approx 10^{-24}}{~ \rm cm}^2</math>. |
Classically, the quadrupole interaction energy is | Classically, the quadrupole interaction energy is | ||
| Line 491: | Line 560: | ||
</math> | </math> | ||
| − | Here <math>\beta</math> is the angle between the quadrupole moment (aligned with '''I''') with the symmetry axis of the electric field gradient (aligned with '''J'''). Therefore, <math> {\rm cos}\beta </math> is proportional to <math>\langle {\bf{I}} \cdot {\bf{J}} \rangle / \hbar^2 = [F(F+1) - J(J+1) - I(I+1)]/2 = C </math> | + | Here <math>\beta</math> is the angle between the quadrupole moment (aligned with '''I''') with the symmetry axis of the electric field gradient (aligned with '''J'''). Therefore, <math> {\rm cos}\beta </math> is proportional to <math>\langle {\bf{I}} \cdot {\bf{J}} \rangle / \hbar^2 = [F(F+1) - J(J+1) - I(I+1)]/2 = C/2 </math> |
Quantum mechanically, the classical <math>{\rm cos}^2\beta </math> term becomes <math> C(C+1)</math>. The resulting energy shifts are then | Quantum mechanically, the classical <math>{\rm cos}^2\beta </math> term becomes <math> C(C+1)</math>. The resulting energy shifts are then | ||
| Line 567: | Line 636: | ||
where the term involving <math>m/M</math> comes from solving the two body system of | where the term involving <math>m/M</math> comes from solving the two body system of | ||
electron (mass <math>m</math>) and nucleus (mass <math>M</math>) using the relative coordinate and | electron (mass <math>m</math>) and nucleus (mass <math>M</math>) using the relative coordinate and | ||
| − | associated reduced mass. | + | associated reduced mass. The finite mass of the nucleus decreases the binding energy of the electron, but this decrease gets smaller with increasing mass of the nucleus (in the limit of infinite mass, the reduced mass is the electron mass). Therefore, increasing <math>M</math> increases <math>E_n</math> and therefore increases transition frequencies (positive shift). |
| + | |||
| + | |||
In two (or more) electron atoms the situation becomes more | In two (or more) electron atoms the situation becomes more | ||
complicated due to the relative motion of the electrons. It | complicated due to the relative motion of the electrons. It | ||
| Line 605: | Line 676: | ||
which decreases as <math>M^{-2}</math>, reaching 10 parts per million for a | which decreases as <math>M^{-2}</math>, reaching 10 parts per million for a | ||
nucleus with <math>A = 54</math> (assuming <math>\Delta M</math> = 1). | nucleus with <math>A = 54</math> (assuming <math>\Delta M</math> = 1). | ||
| + | |||
| + | <p></p> | ||
=== Volume effect === | === Volume effect === | ||
| Line 616: | Line 689: | ||
distribution, causing a further rise in its energy. This | distribution, causing a further rise in its energy. This | ||
reduction in the binding energy results in a decrease of the | reduction in the binding energy results in a decrease of the | ||
| − | transition energy and therefore to a negative mass shift | + | transition energy, and the decrease is larger for heavier (and therefore larger) nuclei. Therefore, the volume effect leads to a negative mass shift, i.e. transition frequencies decrease with increasing isotope mass. |
(assuming that the <math>S</math> state is the lower energy state | (assuming that the <math>S</math> state is the lower energy state | ||
involved in the transition). | involved in the transition). | ||
| Line 628: | Line 701: | ||
</ul> | </ul> | ||
<br style="clear: both" /> | <br style="clear: both" /> | ||
| + | [[Category:8.421]] | ||
Latest revision as of 02:05, 23 March 2020
Contents
Overview
Until now we have discussed atoms as if the nuclei were point charges with no structure and infinite mass. Real nuclei have finite mass, possibly non-zero angular momentum, , and a charge which is spread out over a finite volume. As a result, they possess magnetic dipole moments and electric quadrupole moments coupled to the angular momentum, and possibly higher moments as well. All of these properties affect the atomic energy levels at a level about rydberg. Here's a catalog of these effects:
Cause Result How Observed Finite Mass Mass Shift Isotope shifts Finite Volume of Charge Volume Shift Magnetic Dipole () Hyperfine structure Energy splittings Electric Quadrupole () Hyperfine structure
The first two effects produce only a small shift of the spectral line, and thus the only quantity accessible to measurement is the variation of the line position between different isotopes of the same element. (In atoms with only one or two electrons it may be possible to predict the position of a line with significant accuracy to deduce the isotope shift absolutely.) Laser spectroscopy makes it possible to measure isotope shifts to at least Ry or of the shift. The moments of the nucleus are aligned with its spin and interact with the angular momentum of the rest of the atom. This couples the angular momenta J and I to the total angular momentum F: , and leads to hyperfine splitting of atomic levels. The resulting hyperfine structure can be measured with almost limitless precision (certainly Rydberg) using the techniques of RF spectroscopy. Hyperfine transitions in Cs and H are currently the best available time and frequency standards. Generally speaking, magnetic dipole interactions predominate in atoms and electric quadrupole interactions in molecules. With the exception of the mass shift, the manifestations of nuclear structure in atomic spectra provide important information on the static properties of nuclei which are among the most precise information about nuclei. Unfortunately the great precision of the atomic measurements is generally lost in deducing information about nuclear structure because the core electrons affect the magnetic and electric interactions of the valence electrons with the nucleus.
Allowable Multipole Moments in Nuclei
Introduction
In general, nuclei are composed of more than one particles, and hence it is possible for nuclei to have multipole moments beyond electric monopole and magnetic dipole. Multipole moments of a nucleus arise from its angular momentum , and the allowed moments are governed by both and symmetry consideration. In this section, we discuss what are the possible multipole moments for nuclei. We shall denote the order of multipoles as follow: monopole , dipole , quadrupole , octopole , etc.
Angular Momentum and Multipole Moments
The multipole moment of a nucleus arises from its angular momentum. To see that, intuitively we know that multipole moment is a consequence of shape. In order to distinguish shapes, one needs be able to distinguish orientation, and it is angular momentum that sets orientation. For example, let us consider a magnetic dipole. In order to measure it, one needs to be able to distinguish between up and down direction, which can be accomplished by passing the dipole through a uniform field and observing whether it moves up or down (Stern-Gerlach experiment).
Q: What is the minimum for dipole moment?
A: As discussed above, in order to oberseve dipole moment, one needs to be able to distinguish up and down. Quantum mechanically, the dipole moment results in two energy levels different from the single energy level of a monopole. This implies one needs to have at least .
Q: What is the minimum for quadrupole moment?
A: Quadrupole moment is basically an ellipse. In order to tell that one has an ellipse, one needs to be able to distinguish not just up and down, but also an orthogonal orientation. It implies three energy levels, and hence .
In general, in order to possess a moment of order , a nucleus needs to have at least .
Formally, let us denote the multipole operator as , where is the angular momentum quantum number of the multipole, and is the azimuthal quantum number. In coordinate space, is the solid harmonics, with the spherical harmonics. The moment of the nucleus is then given by . Now, we know the component involving azimuthal quantum number decouples from the angular quantum numbers: . Whether the angular component has non-zero value tells us whether the particular moment is forbidden given the . Specifically, one can pick . The angular dependence of the first few spherical harmonics are given here:
Graphically, one can imagine the "triangle rule". Consider a vector , and asks how can one add to get . It is possible only when is at least . And hence one also obtains the same condition .
Symmetry Consideration
Besides angular momentum consideration, parity symmetry further restricts what specific electric and magnetic multipoles are allowed in a nucleus. Let us begin with an example: can a nucleus possesses a permanent electric dipole moment? Assuming an electric dipole moment is possible, let us apply parity transformation on the nucleus. Electric dipole moment has odd parity and thus changes sign. Therefore, a permanent electric dipole moment is forbidden by parity symmetry. On the other hand, a magnetic dipole moment does not change sign under parity transformation and thus is allowed.
In general, the parity of the multipoles is as follow:
Electric multipole of order : Magnetic multipole of order :
Therefore, we see that even electric multipoles ( monopole, quadrupole, ...) and odd magnetic multipoles ( dipole, octopoles, ...) are the only allowed multipole moments.
In summary, we see that symmetry consideration allows a nuclues to have even electric multipoles and odd magnetic multipoles. In addition to these restrictions, angular momentum consideration limits the multipole orders to .
Hyperfine interaction
Introduction
Hyperfine structure, as its name suggests, is extremely small on the scale of atomic interactions. To give an idea of its size, note that fine structure, which arises from relativistic effects and the spin- orbit interaction, is (i.e. of order on the scale of atomic interactions). The magnetic hyperfine interaction, which arises from the interaction of the nuclear magnetic moment with the surrounding electrons, is , which is approximately 2000 times smaller. Nevertheless, studies of hyperfine structure have played an important role in the determination of nuclear properties. Perhaps more relevant today is the role of hyperfine structure in many laser-atomic experiments, particularly those that involve manipulating atoms with light. This is because hyperfine structure affects the optical selection rules and the transfer of momentum and angular momentum to atoms by light. The magnetic hyperfine interaction is most important for atoms with an unpaired electron. Consequently, the alkali-metal atoms, which are the workhorses for laser-atomic physics, all display prominent hyperfine structure, sometimes to the despair of the experimenter.
The fact that the nucleus is a charge cloud with angular momentum suggests the possibility that it might possess magnetic and electric moments. Time reversal and parity invariance restrict the possible magnetic moments to dipole, octopole, ... and the possible electric moments to monopole (), quadrupole... The magnetic dipole and electric quadrupole interactions are dominant in the hyperfine interaction. The magnetic dipole moment can be measured only if the nucleus has , and it splits only those levels for which 1/2. Similarly, the electric quadrupole interaction is observable only when and are both 1. Note that the units used in this section are Gaussian electro-static units (ESU).
Semi-classical analysis of the magnetic hyperfine interaction
The magnetic moment of the nucleus is generally expressed in terms of the nuclear magneton,
and the nuclear g-factor,
In some cases it is convenient to express the nuclear moment in terms of the Bohr magneton. This is done by defning the g-factor by
To emphasize the fact that the nuclei are complex particles we note that the g-factors of the neutron and proton are
neither one of which is close to a simple integer. The magnetic moment of the nucleus couples to the magnetic field produced at the nucleus by the electrons in the atom. As a result and are coupled together to form , the total angular momentum of the entire atom
The magnetic coupling between and adds a term to the Hamiltonian for the magnetic dipole hyperfine structure which is the interaction between a nucleus with magnetic moment , and the magnetic field due to a single valence electron.
The electron's magnetic field is proportional to its angular momentum { }, and so we can write
Writing as , we have <equation id="EQ_cathree" noautocaption> (%i) </equation> The constant is called the hyperfine coupling constant. By convention, it is written in units of frequency. There are two contributions to , orbital and spin: . We shall first evaluate the fields classically. The magnetic moment of the electron is given by
where is the Bohr magneton. (The negative sign is taken by convention, so that is a positive number.) Then,
<equation id="EQ_caseven" noautocaption> (%i) </equation> We need to evaluate
Using , , and , we obtain
So after all this work, the field turns out to depend only on . From <xr id="EQ_cathree"/>, we obtain
For a hydrogenic atom with
Writing , we finally obtain
-states require a separate treatment: diverges for -states.
The orbital magnetic field is absent in -states. However, the electron has finite probability of being at the origin and it must be regarded as a magnetic "cloud" with magnetization
The magnetization gives rise to a field at the origin
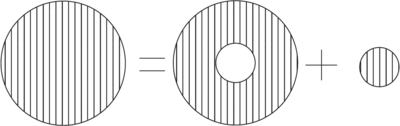
- Decomposition of a spherically symmetric cloud of magnetization for finding the field at its center.
The magnetization can be viewed as the sum of a small uniform sphere at the origin, plus a hollow sphere containing the remainder of the magnetization. It is easily shown that the field due to the hollow sphere vanishes. However, the uniform sphere give rise to a finite value of due to an equivalent surface magnetic charge density
which acts as the source of { }.
Since , <equation id="EQ_caeighteen" noautocaption> (%i) </equation> This -state interaction is often called the "contact" (in the sense of touch) term. We can summarize these results by combining <xr id="EQ_caseven"/> and <xr id="EQ_caeighteen"/> taking = 2: <equation id="EQ_caninteen" noautocaption> (%i) </equation> The first three terms in the bracket average to zero in an -state; the last term contributes only in an -state.
Quantum mechanical treatment
The nucleus gives rise to the vector potential
The atomic Hamiltonian is
(We continue to use the convention that is the magnitude of the electron charge.) The last term describes the interaction of the electron and the magnetic field due to the nucleus. We can write , where, neglecting the term in <equation id="EQ_qmt3" noautocaption> (%i) </equation> We can take to obey the Coulomb gauge . Then the first term in Eq. <xr id="EQ_qmt3"/> gives
and
The second term can be transformed using
Using this result, the second term in Eq. <xr id="EQ_qmt3"/> can be written
In a spherical state the average of the first factor in the bracketed term becomes
plus cross terms which average to zero. Consequently,
which is cancelled by the second factor. For states that vanish at the origin,
Taking , we have
where it is understood that the first term vanishes in states. We finally obtain
Writing this as , we obtain the result found by the classical argument, Eq. <xr id="EQ_caninteen"/>.
Hyperfine structure at zero magnetic field
The Hamiltonian at zero magnetic field is
The total angular momentum is . In zero or low field, and are good quantum numbers. A "good" quantum number is the eigenvalue of an operator that (approximately) commutes with the Hamiltonian, so that it is not perturbed by simple time evolution. At zero field, for instance, eigenfunctions of are eigenfunctions of . Physically, and are tightly coupled by the interaction: they precess about each other, and about . Using , we obtain
and for the energy levels
Note that remains a good quantum number at all fields. (The symbols and are used both for operators and eigenvalues: the meaning is clear from the context). has values , . The interval between adjacent terms is
This result, known as the Lande Interval Rule, played an important role in the early development of the theory of hyperfine structure. Furthermore, it is easy to show that
so that the "center of gravity" of a hyperfine multiplet is zero.
For s state atoms, only the contact term contributes to the hyperfine constant:
For hydrogen in the 1s ground state, ah=1420 MHz. The hyperfine interaction splits the ground state into an F=1 component (shifted up by ah/4) and an F=0 component (shifted down by 3 ah/4).
Electric quadrupole interaction
If the nucleus does not have a spherically symmetric charge distribution, it probably has a non-zero electric quadrupole moment
which is for an oblate charge distribution. In contrast to the nuclear magnetic dipole, which is predominantly determined by the unpaired nucleons, is sensitive to collective deformations of the nucleus. Some nuclei are observed with 30 % differences between polar and equatorial axes, so can be comparable to , i.e.~.
Classically, the quadrupole interaction energy is
Here is the angle between the quadrupole moment (aligned with I) with the symmetry axis of the electric field gradient (aligned with J). Therefore, is proportional to
Quantum mechanically, the classical term becomes . The resulting energy shifts are then
where
and
[Note that , which was involved in , is equal to ].
Note: The preceding expressions, like the corresponding ones for the magnetic interactions, have several significant omissions. The most important are relativistic corrections and core shielding corrections. Calculations of core shielding have been made by Sternheimer \cite{Sternheimer1967}, and the quadrupole shielding by the core is sometimes prefixed by his name.
Order of magnitude of hyperfine structure
In general the magnetic hyperfine structure dominates electric hyperfine structure in atoms. The opposite is generally true in molecules for two reasons: unpaired electrons are relatively rare, and the molecular binding mechanism can create large electric field gradients at the sites of the nuclei. In concluding this discussion of hyperfine structure in atoms I would like to point out that the preceding formulae are, except in hydrogenic atoms, only approximations and never permit one to extract the nuclear dipole or quadrupole moment with the full accuracy of laser spectroscopy experiment---let alone R.F. spectroscopy experiments. Thus and in the combined hyperfine energy formula
should be regarded primarily as empirical constants from the standpoint of atomic physics. Even if the problems of connecting and with the nuclear moments could be solved, the principal result would be better measurements of nuclear properties.
Isotope Effects
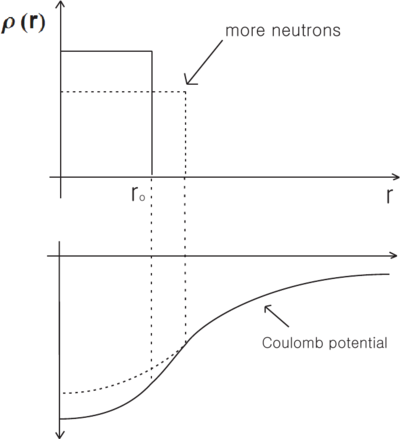
When comparing the spectral lines originating from atoms whose nuclei differ only in the number of neutrons (eg. different isotopes of the same element), effects due to the finite mass and volume of the nucleus become apparent. Even neglecting hyperfine structure (by taking the center of gravity of the observed splitting), the spectral lines of the different isotopes vary slightly in position---generally at the many parts per million level. The difference between the lines of the various isotopes is referred to as the isotope shift: it is observed to have both positive (heavier isotope has higher energy spacing) and negative values. General speaking, light () elements have positive frequency shift whereas heavy elements () have negative shifts. This reflects the contribution of two distinct physical processes to the shift; the finite mass shift (almost always positive), and the nuclear volume shift (almost always negative). These will be discussed separately.
Mass effect
The origin of the mass effect is obvious from the Bohr energy level formula
where the term involving comes from solving the two body system of electron (mass ) and nucleus (mass ) using the relative coordinate and associated reduced mass. The finite mass of the nucleus decreases the binding energy of the electron, but this decrease gets smaller with increasing mass of the nucleus (in the limit of infinite mass, the reduced mass is the electron mass). Therefore, increasing increases and therefore increases transition frequencies (positive shift).
In two (or more) electron atoms the situation becomes more
complicated due to the relative motion of the electrons. It
would, for example, be possible to arrange the electrons
symmetrically on opposite sides of the nucleus in which case
there would be zero isotope effect. The virial theorem assures
us that the mean value of the kinetic energy equals the negative
of the total energy, so if we treat the nuclear motion as a
perturbation on a fixed nucleus solution, the mass effect will be:
The first term is called the normal shift since (using the virial theorem again) it is
The second term is called specific because it depends on the atom's quantum state. A discussion can be found in Sobel'man (pp. 224-6). unless there are two or more valence electrons.
The fractional energy shift of a level due to the mass of the nucleus decreases rapidly with increasing mass of the nucleus. The normal part of this shift has a variation in the fractional magnitude due to a change in the mass of the isotope of
which decreases as , reaching 10 parts per million for a nucleus with (assuming = 1).
Volume effect
Inside the nucleus, the electrostatic potential no longer behaves like , but is reduced from this value. If the valence electron(s) penetrate significantly into this region (eg. for electrons) then its energy will rise, relative to the value for a point nucleus, because of this reduced potential. Adding neutrons to the nucleus generally spreads out the charge distribution, causing a further rise in its energy. This reduction in the binding energy results in a decrease of the transition energy, and the decrease is larger for heavier (and therefore larger) nuclei. Therefore, the volume effect leads to a negative mass shift, i.e. transition frequencies decrease with increasing isotope mass. (assuming that the state is the lower energy state involved in the transition).
- Simplified example of volume effect.
References
- Fermi1933: E. Fermi and E. Segré. Memorie dell Accademia d'Italia, 4:131, 1933. An English translation is in Hindmarsh p. 259.
- Sternheimer1967: R. M. Sternheimer. Quadrupole shielding and antishielding factors for atomic states. Phys. Rev., 164(1):10–20, Dec 1967.
































































![{\displaystyle {\bf {B}}_{S}(0)=-{\frac {1}{r^{3}}}{\left[{\bf {\mu }}_{e}-3({\bf {\mu }}_{e}\cdot {\bf {\hat {r}}}){\bf {\hat {r}}}\right]}=+g_{e}{\frac {\mu _{B}}{r^{3}}}{\left[{\bf {S}}-3({\bf {S}}\cdot {\bf {\hat {r}}}){\bf {\hat {r}}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a27af534f9c3323efed87150815e4f44e048aba)
![{\displaystyle {\bf {B}}_{J}(0)=-{\frac {2\mu _{B}}{r^{3}}}{\left[{\bf {L}}-{\frac {g_{e}}{2}}({\bf {S}}-3({\bf {S}}\cdot {\bf {\hat {r}}}){\bf {\hat {r}}})\right]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7ad0cbe8ed9883515417493edd2462e67bb6f37)
![{\displaystyle \langle {{\bf {J}}\cdot {\bf {B}}_{J}}\rangle =-{\frac {2\mu _{B}}{r^{3}}}[\ell (\ell +1)-S(S+1)+\langle {3({\bf {S}}\cdot {\bf {\hat {r}}}){\bf {\hat {r}}}\cdot ({\bf {L}}+{\bf {S}})}\rangle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a876322671ec6f31798ef7bc2d110be32b0215b2)





















![{\displaystyle {\bf {B}}(0)=-2\mu _{B}{\left[{\frac {\bf {L}}{r^{3}}}-{\frac {\bf {S}}{r^{3}}}+{\frac {3({\bf {S}}\cdot {\bf {\hat {r}}}){\bf {\hat {r}}}}{r^{3}}}-{\frac {8}{3}}\pi \delta ({\bf {r}}){\bf {S}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10228d2734354c2fe3c7278c3c7c6d896df4f0db)











![{\displaystyle \nabla \times {\left[{\frac {{\bf {\mu }}_{I}\times {\bf {r}}}{r^{3}}}\right]}=-\nabla \times {\left[{\bf {\mu }}_{I}\times \nabla {\frac {1}{r}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3263b311b209f65a42b1c365c0d44cf345fec6e)
![{\displaystyle H_{\text{hf}}^{\text{spin}}=g_{e}\mu _{B}{\left[({\bf {S}}\cdot \nabla )({\bf {\mu }}_{I}\cdot \nabla {\frac {1}{r}})-{\frac {1}{3}}{\bf {S}}\cdot {\bf {\mu }}_{I}\nabla ^{2}{\frac {1}{r}}\right]}-{\frac {2}{3}}g_{e}\mu _{B}{\bf {S}}\cdot {\bf {\mu }}_{I}\nabla ^{2}{\frac {1}{r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cf3d859cb717a4c1b34653c8f7c9c509f597650)




![{\displaystyle H_{\text{hf}}^{\text{spin}}=-2\mu _{B}{\left[{\frac {{\bf {S}}\cdot {\bf {\mu }}_{I}}{r^{3}}}-{\frac {3({\bf {S}}\cdot {\hat {r}})({\bf {\mu }}_{I}\cdot {\hat {r}})}{r^{3}}}\right]}-16{\frac {\pi }{3}}\mu _{B}{\bf {S}}\cdot {\bf {\mu }}_{I}\delta ({\bf {r}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45a47644c4bf7e59cb7f6bfde6fbaf8c8f77e85)
![{\displaystyle H_{\text{hf}}=2\mu _{B}{\frac {\mu _{I}}{I}}{\bf {I}}\cdot {\left[{\frac {1}{r^{3}}}({\bf {L}}-{\bf {S}}+3({\bf {S}}\cdot {\bf {\hat {r}}}){{\bf {\hat {r}}})}-{\frac {8\pi }{3}}{\bf {S}}\delta ({\bf {r}})\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f860bba0f5266873a84fdf26651a86eab9f650e0)







![{\displaystyle \langle {{\bf {I}}\cdot {\bf {J}}}\rangle =[F(F+1)-J(J+1)-I(I+1)]/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c14f6201c751d18d948e483dea07686de44239a5)
![{\displaystyle W(F,m)={\frac {ah}{2}}[F(F+1)-J(J+1)-I(I+1)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fac8718bef37befda669c85608de2397dd810d36)







![{\displaystyle Q={\frac {1}{e}}\int d^{3}r\rho ({\bf {r}})[3z^{2}-r^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d94a3b0f28dbed2da81545ffdcdd6a63eb1c0577)







![{\displaystyle \langle {\bf {I}}\cdot {\bf {J}}\rangle /\hbar ^{2}=[F(F+1)-J(J+1)-I(I+1)]/2=C/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd35b26e67450e1f862cd81f5d7d8400d1c236c)




![{\displaystyle C=[F(F+1)-J(J+1)-I(I+1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/186634bc734a87c263edc7be08d632d86fdd8077)












![{\displaystyle \Delta E_{n,M}={\frac {-p^{2}}{2M}}=-{\frac {1}{2M}}{\left[\sum _{i}{\bf {p}}_{i}\right]^{2}}=-{\frac {m}{M}}\left[\underbrace {{\frac {1}{2m}}\sum p_{i}^{2}} _{\rm {NormalShift}}+\underbrace {{\frac {1}{2m}}\sum _{i\not =j}{\bf {p}}_{i}\cdot {\bf {p}}_{j}} _{\rm {SpecificShift}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da3256fc3091bc9a82cfe32ddc282aac7cfb5c5b)