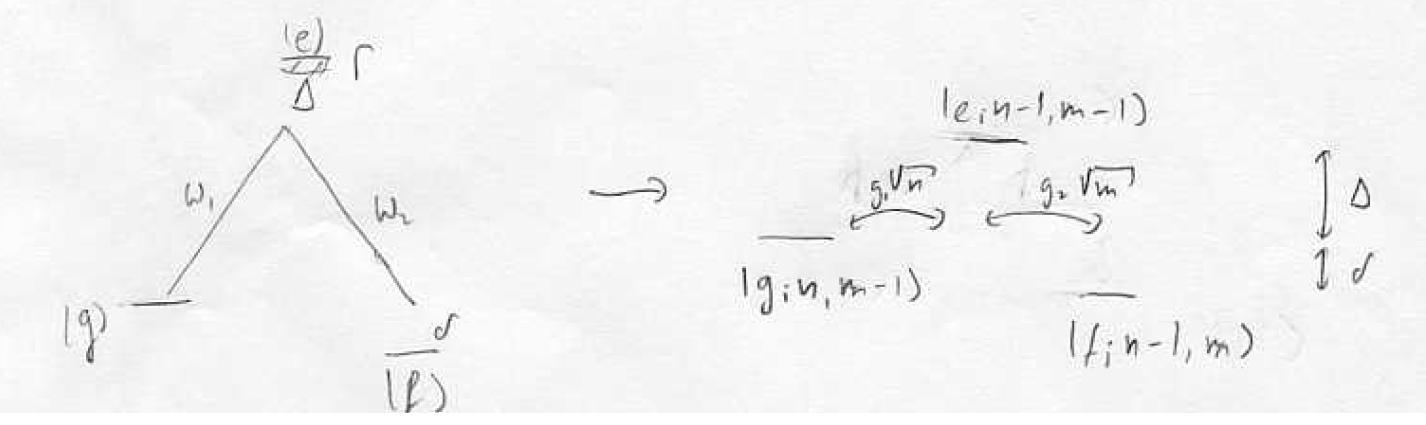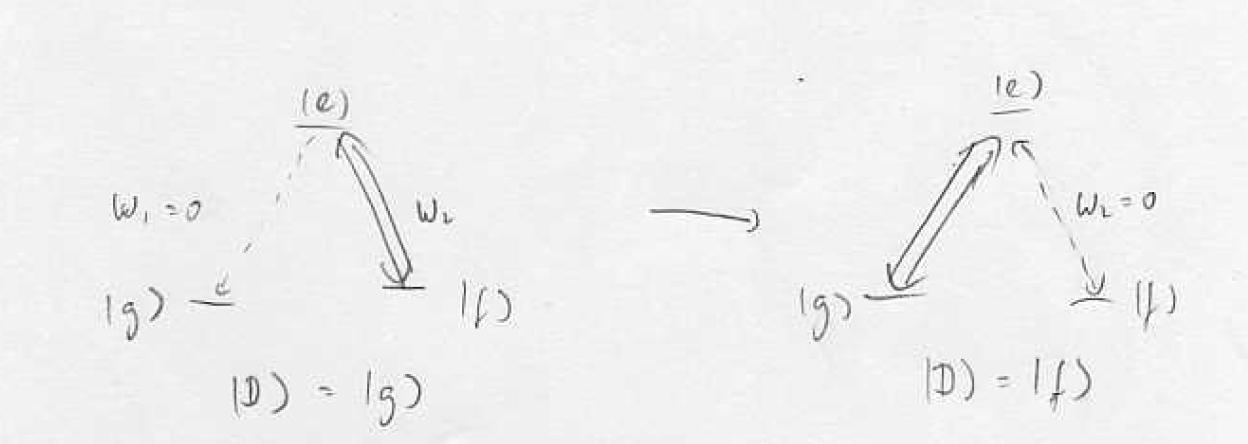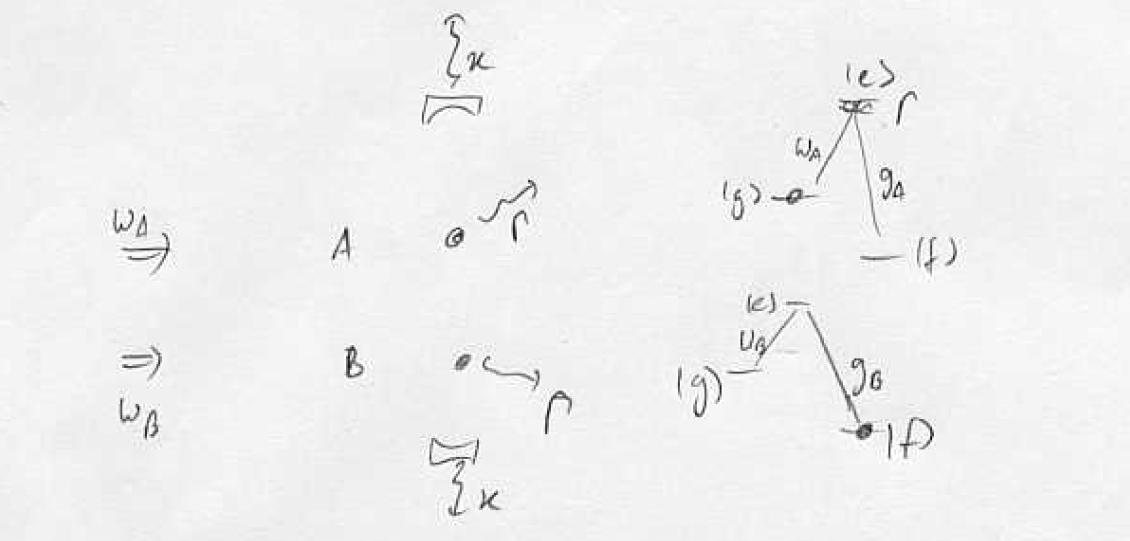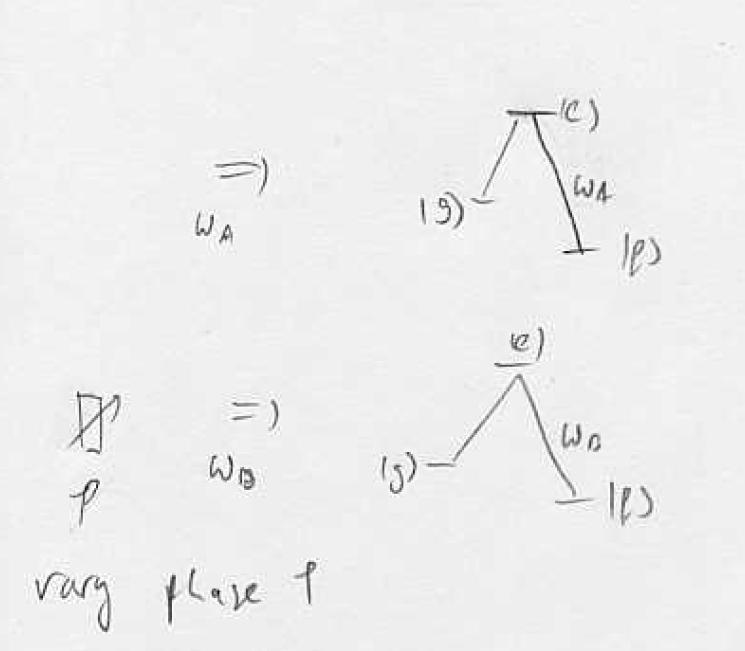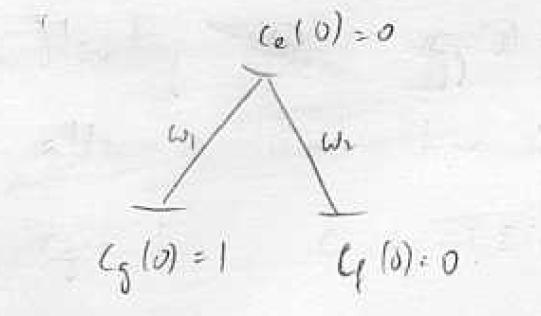Difference between revisions of "Tmp Lecture 24"
imported>Edwardsu m |
imported>Edwardsu |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
== EIT: Eigenstates picture == | == EIT: Eigenstates picture == | ||
| − | Using the field quantization to easily include energy conservation, we see that the states are coupled in triplets: | + | Using the field quantization to easily include energy conservation, we see that the states are coupled in triplets: |
| − | Image | + | [[Image:L24tmpfig1.JPG]] |
So the Hamiltonian is given by <math>\stackrel{\frac{\omega _1}{2}=g_ z\sqrt {n}}{\frac{\omega _2}{2}=g_ z\sqrt {m}}</math> | So the Hamiltonian is given by <math>\stackrel{\frac{\omega _1}{2}=g_ z\sqrt {n}}{\frac{\omega _2}{2}=g_ z\sqrt {m}}</math> | ||
| Line 14: | Line 11: | ||
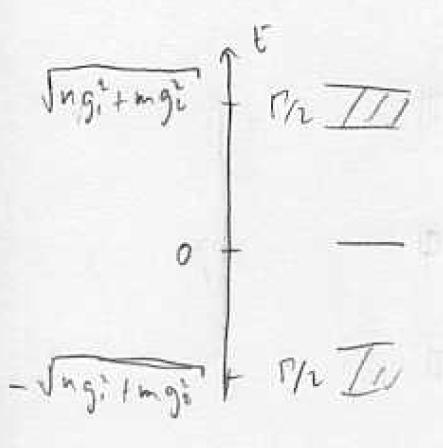
On resonance <math>\Delta =\delta =0_1</math> the Eigenstates are | On resonance <math>\Delta =\delta =0_1</math> the Eigenstates are | ||
| − | Image | + | [[Image:L24tmpfig2.JPG]] |
| − | <math>C,''|g>+C_2''|e>+C_3''|f>=|BI></math> <math>C,|g>+C_3|f>=|D></math> <math>C',|g>+C'_2|e>+C_3'|f>=|BII></math> | + | :<math>C,''|g>+C_2''|e>+C_3''|f>=|BI></math> <math>C,|g>+C_3|f>=|D></math> :<math>C',|g>+C'_2|e>+C_3'|f>=|BII></math> |
In the limit of weak probe and a strong pump, | In the limit of weak probe and a strong pump, | ||
| − | Image | + | [[Image:L24tmpfig3.JPG]] |
we can limit the analysis to <math>n=0,1,m\gg 1</math>. Then we can diagonalize the strong coupling, and treat the probe perturbatively | we can limit the analysis to <math>n=0,1,m\gg 1</math>. Then we can diagonalize the strong coupling, and treat the probe perturbatively | ||
| − | + | [[Image:L24tmpfig4.JPG]] | |
| − | |||
| − | Image | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Again we have a scattering problem <math>|g,|>\otimes |0...0>\rightarrow |g,0>\otimes |...0|_{\kappa _1}0...></math> | Again we have a scattering problem <math>|g,|>\otimes |0...0>\rightarrow |g,0>\otimes |...0|_{\kappa _1}0...></math> | ||
| Line 42: | Line 29: | ||
<math>M=\frac{<g,0|V'|BI><BI|V|g,|>}{-\frac{\Delta }{2}}+\frac{<g,0'|V'|BII><BII|V|g,|>}{\frac{\Delta }{2}}</math> | <math>M=\frac{<g,0|V'|BI><BI|V|g,|>}{-\frac{\Delta }{2}}+\frac{<g,0'|V'|BII><BII|V|g,|>}{\frac{\Delta }{2}}</math> | ||
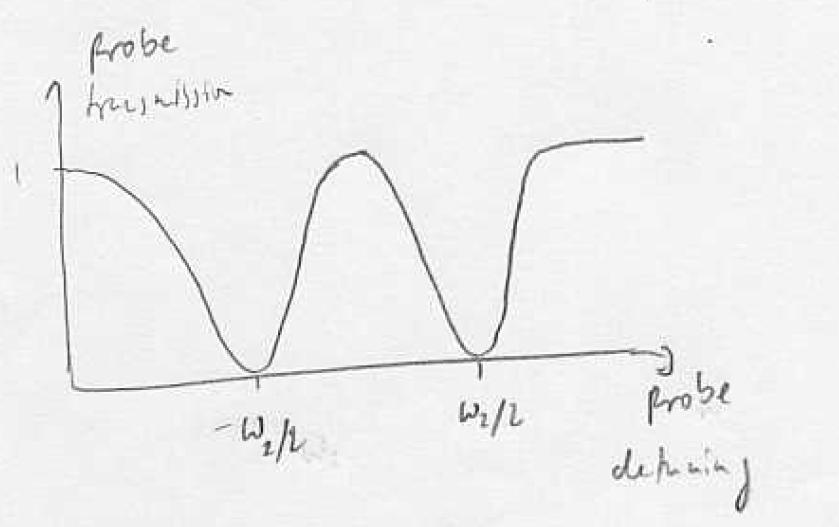
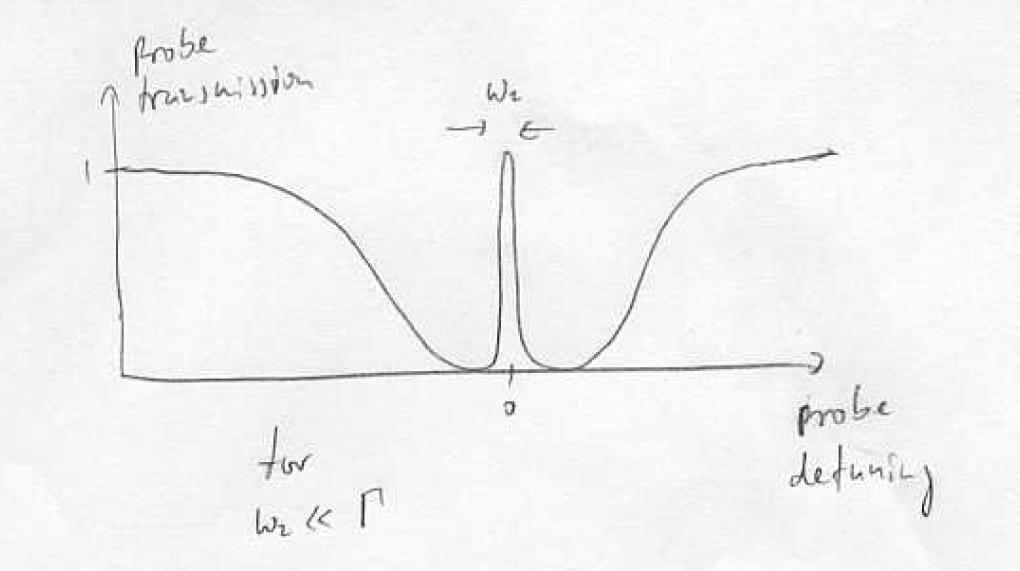
| − | On one- and two-photon resonance all couplings are symmetric in <math>|BI></math> and <math>|B2></math>, the detunings are opposite, and the matrix element M vanishes: electromagnetically induced transparency (EIT). If the pump remains on resonance and we tune the probe field, then the couplings are still symmetric in <math>|BI></math>, <math>|B2></math>, but the detunings are <math>\frac{(\Delta \pm \delta )}{2}</math>, and the matrix element does not vanish. Maximum scattering is obtained when we tune to one of the | + | On one- and two-photon resonance all couplings are symmetric in <math>|BI></math> and <math>|B2></math>, the detunings are opposite, and the matrix element M vanishes: electromagnetically induced transparency (EIT). If the pump remains on resonance and we tune the probe field, then the couplings are still symmetric in <math>|BI></math>, <math>|B2></math>, but the detunings are <math>\frac{(\Delta \pm \delta )}{2}</math>, and the matrix element does not vanish. Maximum scattering is obtained when we tune to one of the bright states |
| − | Image | + | [[Image:L24tmpfig5.JPG]] |
| − | Image | + | [[Image:L24tmpfig6.JPG]] |
When we include the decay <math>|e>\rightarrow |g>,|f></math> within the system, we can no longer use the Hamiltonian formalism, but must use density matrices. Nevertheless, the eigenstates provide physical insight into the problem. | When we include the decay <math>|e>\rightarrow |g>,|f></math> within the system, we can no longer use the Hamiltonian formalism, but must use density matrices. Nevertheless, the eigenstates provide physical insight into the problem. | ||
| Line 53: | Line 40: | ||
== STIRAP in a three-level system == | == STIRAP in a three-level system == | ||
| − | Image | + | [[Image:L24tmpfig7.JPG]] |
If at least one of the two coupling beams is non-zero, there is always a finite energy spacing between the dark state and the bright states. This allows one, by changing the ration of the coupling beams, to adiabatically change the character of the dark state between |g> and |f> while not populating the bright states (and thus the excited state). By use of the so-called "counterintuitive pulse sequence" | If at least one of the two coupling beams is non-zero, there is always a finite energy spacing between the dark state and the bright states. This allows one, by changing the ration of the coupling beams, to adiabatically change the character of the dark state between |g> and |f> while not populating the bright states (and thus the excited state). By use of the so-called "counterintuitive pulse sequence" | ||
| − | + | [[Image:L24tmpfig8.JPG]] | |
STIRAP of this type in a three-level system is also called "dark-state transfer." | STIRAP of this type in a three-level system is also called "dark-state transfer." | ||
| Line 64: | Line 51: | ||
== Example: Five-level non-local STIRAP == | == Example: Five-level non-local STIRAP == | ||
| − | + | [[Image:L24tmpfig9.JPG]] | |
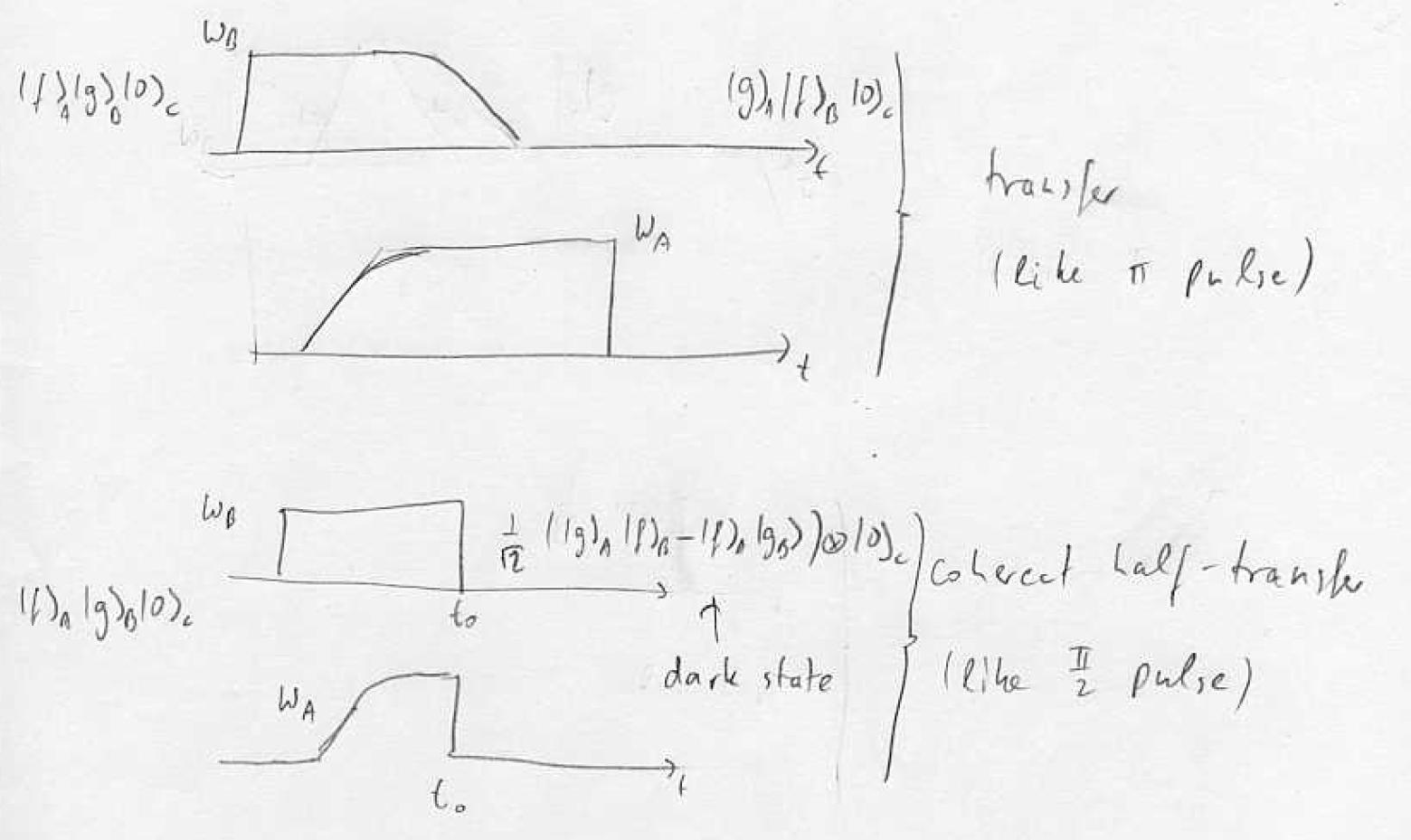
Atom A contains hyperfine excitation, can we transfer the hyperfine excitation from A to B without losing it from the cavity? Cavity strongly coupled to A,B with single-photon Rabi frequency g. Dark-state adiabatic transfer with virtual excitation of the cavity mode is possible: | Atom A contains hyperfine excitation, can we transfer the hyperfine excitation from A to B without losing it from the cavity? Cavity strongly coupled to A,B with single-photon Rabi frequency g. Dark-state adiabatic transfer with virtual excitation of the cavity mode is possible: | ||
| − | + | [[Image:L24tmpfig10.JPG]] | |
| − | Procedure: turn on <math>\omega _ B</math> first coupling empty level, ramp up <math>\ | + | Procedure: turn on <math>\omega _ B</math> first coupling empty level, ramp up <math>\omega_A</math>, ramp down <math>|\omega_ B\rightarrow </math> adiabatic transfer <math>|g_ A>|\delta >_ B|0>_ c\rightarrow |\delta >_ A|g>_ B|0>_ c</math> via dark state of the cavity. Note that the probability to find the photon in the cavity can be made very small while maintaining full transfer: virtual states. |
| − | + | [[Image:L24tmpfig11.JPG]] | |
If we stop the transfer suddenly half-way we create an entangled state where the single hyperfine excitation is shared between the two samples. | If we stop the transfer suddenly half-way we create an entangled state where the single hyperfine excitation is shared between the two samples. | ||
| Line 82: | Line 69: | ||
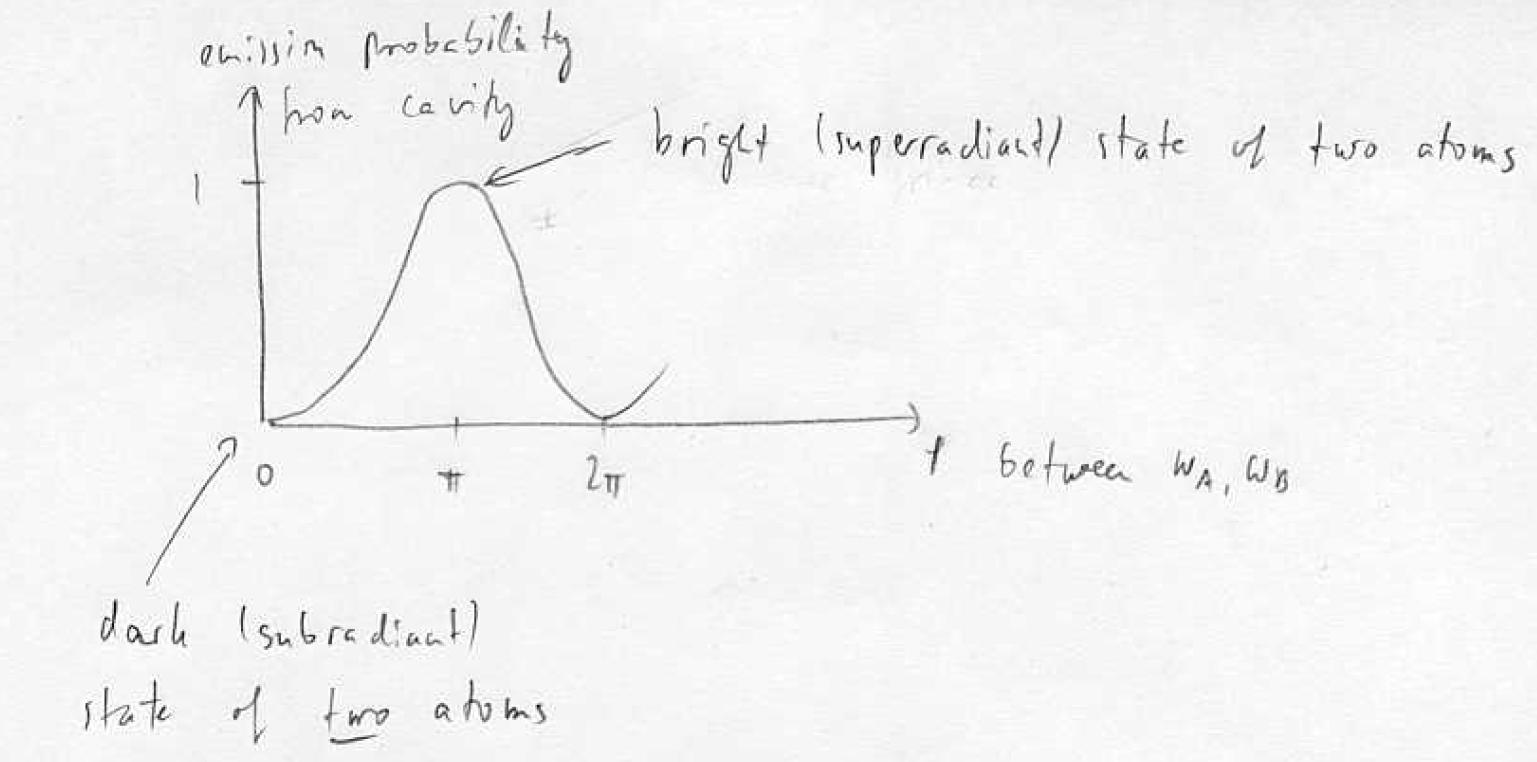
How to verify? Simultaneous readout, super and sub radiant states | How to verify? Simultaneous readout, super and sub radiant states | ||
| − | + | [[Image:L24tmpfig12.JPG]] | |
The dipole moments <math>d_{ge}</math> (emitted fields on the ge transition) of the two atoms can interfere. | The dipole moments <math>d_{ge}</math> (emitted fields on the ge transition) of the two atoms can interfere. | ||
| − | Image | + | [[Image:L24tmpfig13.JPG]] |
Interference fringe can only be observed if state is entangled. Fringe is due to interference if dipole moments between <underline> | Interference fringe can only be observed if state is entangled. Fringe is due to interference if dipole moments between <underline> | ||
| Line 97: | Line 84: | ||
== On the "magic" of dark-state adiabatic transfer == | == On the "magic" of dark-state adiabatic transfer == | ||
| − | Image | + | [[Image:L24tmpfig14.JPG]] |
How is it that we can transfer the population completely form state |g> to state |f> through the state |e> while keeping the unstable state |e> unpopulated? (The correct statement is "...while keeping the population of |e> negligibly small"). This is possible through coherence-interference: n resonance the eqs of motion for the amplitude read | How is it that we can transfer the population completely form state |g> to state |f> through the state |e> while keeping the unstable state |e> unpopulated? (The correct statement is "...while keeping the population of |e> negligibly small"). This is possible through coherence-interference: n resonance the eqs of motion for the amplitude read | ||
| − | |||
| − | |||
:<math>\begin{align} i\left( \begin{array}{c} C_ g \\ C_ e \\ C_ f \end{array} \right) = \left( \begin{array}{ccc} 0 & \frac{\omega _1}{2} & 0 \\ \frac{\omega _1}{2} & 0 & \frac{\omega _2}{2} \\ 0 & \frac{\omega _2}{2} & 0 \end{array} \right) \left( \begin{array}{c} C_ g \\ C_ e \\ C_ f \end{array} \right) \end{align}</math> | :<math>\begin{align} i\left( \begin{array}{c} C_ g \\ C_ e \\ C_ f \end{array} \right) = \left( \begin{array}{ccc} 0 & \frac{\omega _1}{2} & 0 \\ \frac{\omega _1}{2} & 0 & \frac{\omega _2}{2} \\ 0 & \frac{\omega _2}{2} & 0 \end{array} \right) \left( \begin{array}{c} C_ g \\ C_ e \\ C_ f \end{array} \right) \end{align}</math> | ||
| Line 107: | Line 92: | ||
<math>\dot{C}_ g=-i\frac{\omega _1}{2}C_ e</math> <math>\dot{C}_ e=-i\frac{\omega _1}{2}C_ g -i\frac{\omega _2}{2}C_ f</math> <math>\dot{C}_ f=-i\frac{\omega _2}{2}C_ e</math> | <math>\dot{C}_ g=-i\frac{\omega _1}{2}C_ e</math> <math>\dot{C}_ e=-i\frac{\omega _1}{2}C_ g -i\frac{\omega _2}{2}C_ f</math> <math>\dot{C}_ f=-i\frac{\omega _2}{2}C_ e</math> | ||
| − | Image | + | [[Image:L24tmpfig15.JPG]] |
For adiabatic transfer we have <math>\omega _2\gg \omega _1</math> and amplitude flow as | For adiabatic transfer we have <math>\omega _2\gg \omega _1</math> and amplitude flow as | ||
| − | Image | + | [[Image:L24tmpfig16.JPG]] |
So we see how |f> accumulates amplitude because it arrives there always with the same phase factor -1, whereas the flow back from |f> into |e> leads to a destructive interference in |e> with the amplitude flow from |g>, keeping the amplitude in |e> small at all times, while the amplitude on |f> keeps growing. If the state |f> were to acquire a random phase <underline> | So we see how |f> accumulates amplitude because it arrives there always with the same phase factor -1, whereas the flow back from |f> into |e> leads to a destructive interference in |e> with the amplitude flow from |g>, keeping the amplitude in |e> small at all times, while the amplitude on |f> keeps growing. If the state |f> were to acquire a random phase <underline> | ||
Latest revision as of 17:40, 2 May 2010
Contents
EIT: Eigenstates picture
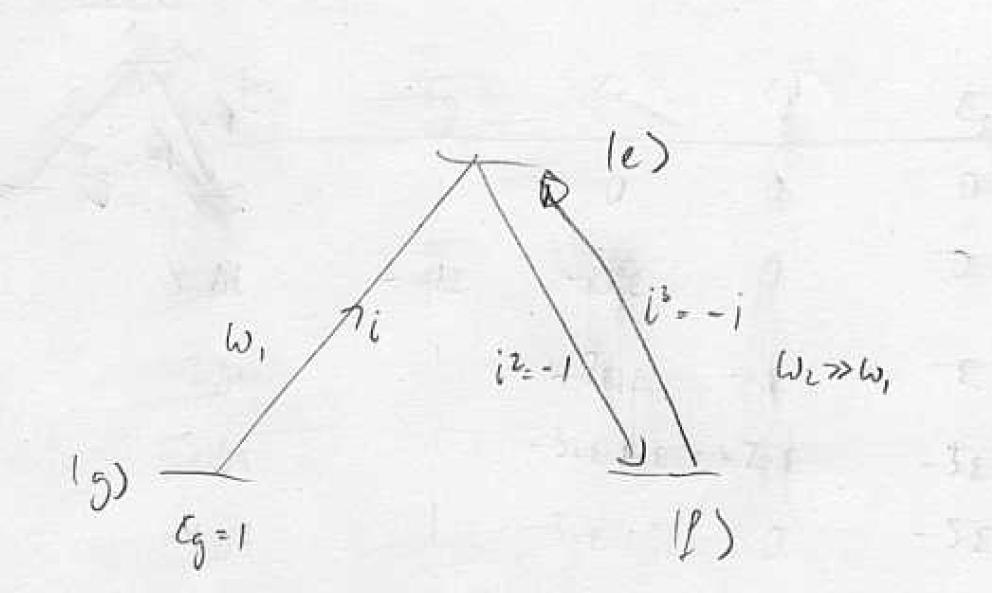
Using the field quantization to easily include energy conservation, we see that the states are coupled in triplets:
So the Hamiltonian is given by
On resonance the Eigenstates are
- :
In the limit of weak probe and a strong pump,
we can limit the analysis to . Then we can diagonalize the strong coupling, and treat the probe perturbatively
Again we have a scattering problem
via a two photon process. The matrix element contains two intermediate states with opposite detunings.
On one- and two-photon resonance all couplings are symmetric in and , the detunings are opposite, and the matrix element M vanishes: electromagnetically induced transparency (EIT). If the pump remains on resonance and we tune the probe field, then the couplings are still symmetric in , , but the detunings are , and the matrix element does not vanish. Maximum scattering is obtained when we tune to one of the bright states
When we include the decay within the system, we can no longer use the Hamiltonian formalism, but must use density matrices. Nevertheless, the eigenstates provide physical insight into the problem.
STIRAP in a three-level system
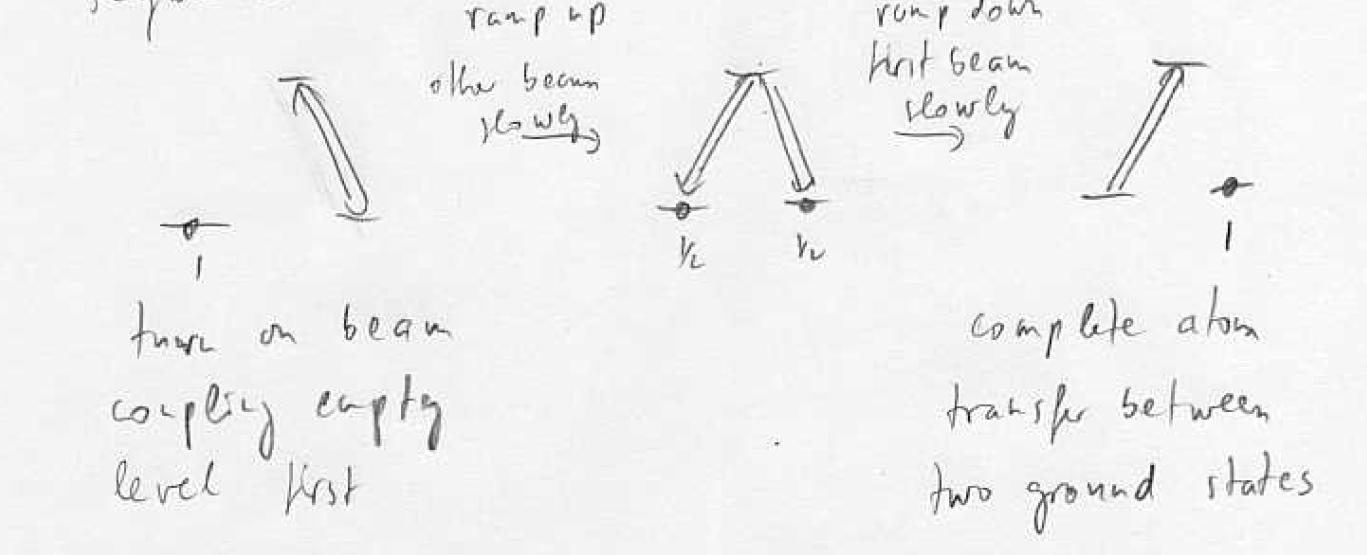
If at least one of the two coupling beams is non-zero, there is always a finite energy spacing between the dark state and the bright states. This allows one, by changing the ration of the coupling beams, to adiabatically change the character of the dark state between |g> and |f> while not populating the bright states (and thus the excited state). By use of the so-called "counterintuitive pulse sequence"
STIRAP of this type in a three-level system is also called "dark-state transfer."
Example: Five-level non-local STIRAP
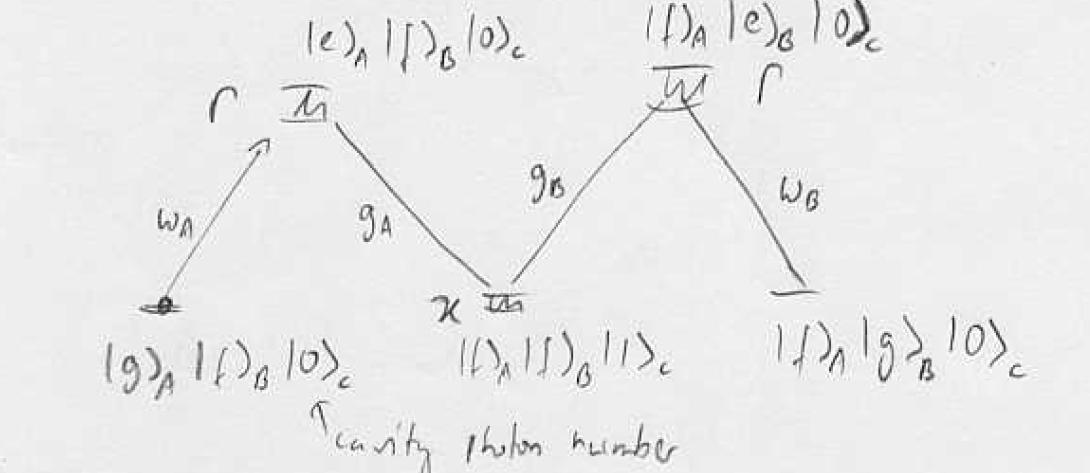
Atom A contains hyperfine excitation, can we transfer the hyperfine excitation from A to B without losing it from the cavity? Cavity strongly coupled to A,B with single-photon Rabi frequency g. Dark-state adiabatic transfer with virtual excitation of the cavity mode is possible:
Procedure: turn on first coupling empty level, ramp up , ramp down adiabatic transfer via dark state of the cavity. Note that the probability to find the photon in the cavity can be made very small while maintaining full transfer: virtual states.
If we stop the transfer suddenly half-way we create an entangled state where the single hyperfine excitation is shared between the two samples.
Verification and entanglement:
well-defined phase must exist
How to verify? Simultaneous readout, super and sub radiant states
The dipole moments (emitted fields on the ge transition) of the two atoms can interfere.
Interference fringe can only be observed if state is entangled. Fringe is due to interference if dipole moments between <underline> <attributes> </attributes> different </underline> atoms.
On the "magic" of dark-state adiabatic transfer
How is it that we can transfer the population completely form state |g> to state |f> through the state |e> while keeping the unstable state |e> unpopulated? (The correct statement is "...while keeping the population of |e> negligibly small"). This is possible through coherence-interference: n resonance the eqs of motion for the amplitude read
For adiabatic transfer we have and amplitude flow as
So we see how |f> accumulates amplitude because it arrives there always with the same phase factor -1, whereas the flow back from |f> into |e> leads to a destructive interference in |e> with the amplitude flow from |g>, keeping the amplitude in |e> small at all times, while the amplitude on |f> keeps growing. If the state |f> were to acquire a random phase <underline> <attributes> </attributes> relative to |g> </underline> due to some other interaction, then the constructive interference leading to the accumulation of amplitude in |f> and the destructive interference in |e> would not work. The dark state transfer requires g-f coherence.