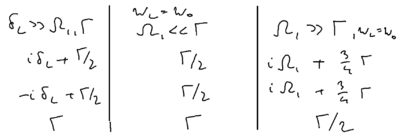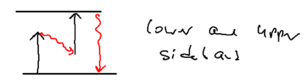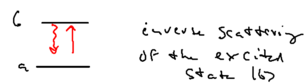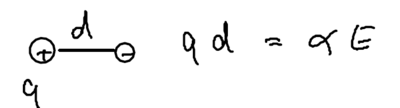Difference between revisions of "Dipole forces and the dressed atom picture"
imported>Ichuang |
imported>Ichuang |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | == Dressed | + | == Dressed atom approach == |
| − | + | {{:Dressed atom approach}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | == Dipole forces within the dressed atom approach == |
| − | + | {{:Dipole forces within the dressed atom approach}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | : | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Category:Light forces]] | [[Category:Light forces]] | ||
Latest revision as of 22:05, 24 April 2009
Contents
- 1 Dressed atom approach
- 2 Dipole forces within the dressed atom approach
- 2.1 Review of the dressed atom picture
- 2.2 Mean dipole force at zero velocity
- 2.3 Mean dipole force at non-zero velocity
- 2.4 Atomic momentum diffusion in the dressed atom picture
- 2.5 Atoms moving in a standing wave: Sisyphus cooling
- 2.6 Dressed atoms in a perturbative limit: cooling in a standing wave
- 2.7 Physics of the dipole force
- 2.8 Four physical pictures of the dipole force
- 2.9 Electric and magnetic components of the dipole force
- 2.10 Energy conservation and dipole forces
- 2.11 References
Dressed atom approach
The dressed atoms picture is one of the most important concepts in modern atomic physics. In this picture, many otherwise complex physical phenomena become clear. For example, we have seen how blue detuned light can perform laser cooling, which was rather counter-intuitive. But if you change basis, and use instead of naked atoms, the dressed atom basis, phenomena such as blue detuned laser cooling become natural and accessible.
The Dressed atoms picture
What is a dressed atom? A dressed atom is an atom plus one mode of the electromagnetic field. We'll come back to that in a moment. On one hand, dressed atoms are nothing new. The dressed atoms picture can be developed from the optical Bloch equations. On the other hand the dressed atoms picture is a language which allows one to better understand what the optical Bloch equations are telling you.
The difference between this treatment, and that of the optical Bloch equations, is that we do not trace out the state of the photon, so we treat the combined state of atom + electromagnetic field. This is actually "half" a difference, because there are two approaches to the dressed atom picture. One emphasizes the photon part of the picture. The second focuses on the atom, treating the electromagnetic field as a classical field. Here, we will focus on the photon, and include the full quantum behavior of the electromagnetic field, at least in setting up the problem.
The dressed atom picture is simply a change of basis. Imagine that you have two pendulums: one representing the atom, the other representing a single electromagnetic mode. From classical mechanics, you know that you can transform in to the basis of the coupled system's eigenmodes. That is what we do in the dressed atom picture. Mathematically, it is almost simplistic, but as you will see it really changes the way you may look at atoms.
Picture of dressed atom scenario
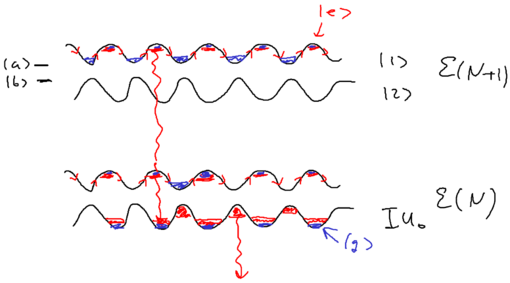
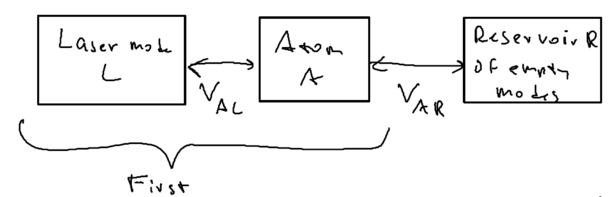
Let us draw a big picture of the Hilbert space we are dealing with:
What is central to this picture is the atom. We allow the atom () to be driven by one mode of the (laser's) electromagnetic field . And we allow the atom to also couple to a reservoir of empty modes; this reservoir is what we used in our study of open quantum systems with master equations. The coupling between atom and photon, is just the Jaynes-Cummings interaction. Previously, we put all of these blocks into one picture.
In this treatment, we couple the atom and photon first, as being the stronger interaction which we diagonalize exactly, then consider the coupling of the coupled system with the rest of the world, the reservoir states.
Coupling Hamiltonian
That means our Hamiltonian has three parts. We have the photon (a simple Harmonic oscillator), the atom, and the rest of the world. The photon and atom Hamiltonians are:
Our first approximation is that we will only interested in resonant physics rather than off-resonant behavior, so we assume the detuning of the photon from the atom is small, . Our states are labeled by the number of photons , and the states of the two-level atom, and .
Define the manifold of states as being , the set of states with total energy . Drawn as energy levels, this is
Our path to the dressed atom picture is thus clearly that we want to diagonalize the coupling in terms of these state manifolds of constant total energy. The coupling Hamiltonian is
The electric field operator is
The dipole operator is
The coupling constant describing this interaction is thus
Energy level splitting at large energy
We apply the coupling Hamiltonian to the two states within each manifold , obtaining the matrix elements
Now we need to consider that we have couplings not only between the two states of the manifold, but also states between manifolds, in the following way. That is, in the rotating wave approximation, we raise the photon number by one and lower the atom. But there are also counter-rotating terms, which raise the photon number while also exciting the atom, or which lower the photon number while also de-exciting the atom. That is, can coupled to , and can couple to . However, these lead to an energy change of two quanta, which are less likely to occur than resonant interactions. We thus neglect such off-shell interactions, with the same rationale as used in the rotating wave approximation.
The couplings of pairs of levels within the manifolds are different, and grow as , and we have seen how this gave rise to the collapse and revival of the photon field as seen in the previous study of the Jaynes-Cummings interaction.
Here we take a different approach, and assume that is large, so that we may approximate , so that the couplings are approximately all the same, , where is the average photon number. We then define the Rabi frequency as
where
The Hamiltonian for each manifold thus becomes, in this approximation,
This is the Hamiltonian for a coupled-Hamiltonian system.
Eigenenergies and anti-crossings
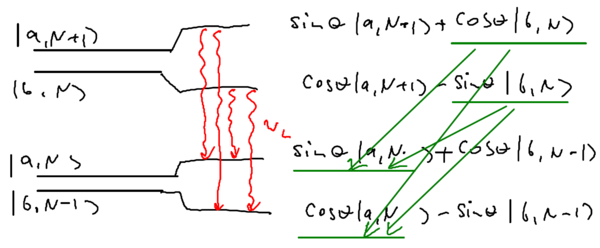
Note that we are presenting the dressed atom picture as a solution of a time-independent Hamiltonian. The solution, given the stationary states under the Jaynes-Cummings evolution, has a generalized Rabi frequency
Pictorially, before the coupling the splitting of energy levels in manifold is , and when the coupling is included the splitting is :
The eigenstates are
where .
Consider the following picture of the energy of the system as a function of the laser frequency , where we take the energy of to be zero:
Note that the energy of the state does not depend on the energy of the laser, while the energy of the state grows linearly with . In the dressed atom picture, the crossing (which happens when there is no coupling) splits into an anti-crossing, with a energy splitting of on resonance. The shift between the dressed energy lines (blue) and the naked state lines (red) is just the AC Stark shift.
Emitted light
Consider, as a first example application of the dressed atom picture, the spectrum of the emitted light from an atom excited by a laser beam.
Weak excitation
First, let the incident laser light have weak intensity. What is the spectrum (that is, the frequency dependence) of the radiation scattered from the atom?
To be as simple as possible, let us give the atom infinite mass (or assume it is trapped deeply in a potential well), such that it cannot move. There are several possibilities you might think of as the correct answer to this question.
The first possibility is that the atom emits with a Lorentzian with linewidth at its frequency . The scond possibility is that it emits with a delta function at frequency . A third possibility is that it emits with a delta function at the laser frequency . And a fourth possibility is that it emits with a Lorentzian with linewidth at frequency .
We have monochromatic energy coming into the system at frequency . The experiment scatters the photons then measures energy again. If you forget everything you know about atomic physics but hold on to the principle of energy conservation, then what answer would you expect?
The answer is very, very clear. If you scatter a single photon, its energy should not change because of energy conservation. Many years ago, beautiful experiments were done (Herbert Walther, 10 years ago), it was shown that the emitted light is a delta function at the frequency of the incident laser .
Lorentizian profiles
The weak excitation scenario leads to a delta function scattered light spectrum. Under what circumstances would you expect to see a Lorentzian broadening? Clearly, the strength of light scattered will follow a lorentzian, as the frequency of the laser is scanned across the atom's resonant frequency.
Thus, if you were to take broadband laser light and shine this light on an atom, the atom would mainly scatter light in a Lorentzian profile around its resonant frequency. The atom acts like a filter, in this sense, but the atom does not broaden the light, it selects from the incident light frequencies.
Strong excitation
When the incident light has strong intensity, then the restrictions of energy conservation are loosened because of the possibility of multi-photon scattering. In this case, in the dressed atom picture, the spectrum of the scattered light now appears as a triplet of lines, known as the Mollow triplet:
There is a delta function at , which has a Lorentzian pedestal of full width half max , and two Lorentians sidebands at of width .
Microscopically, there is a correlation evident in the spectrum, where if a single lower sideband photon is emitted, that is followed by an upper sideband photon, thus satisfying energy conservation.
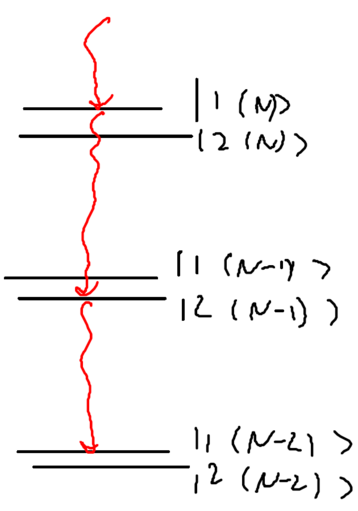
Where does this spectrum come from? Recall the energy levels of the dressed atom picture:
Quantitaive understanding of relative intensities
Keep in mind that the spacing between manifolds is . We can obtain quantitative information about the scattered spectrum with the dressed atom picture. This is because only part of the wavefunction in each superposition state is responsible for the scattered light. For example, a photon emitted from the to has to start from and must end in .
These decompositions tell us what the intensities of the lines in the triplet are. In particular, we can write a table of the transition frequencies and rates expected:
| Frequency | Rate |
Equilibrium populations
The relative intensities are given by population times the rate. We therefore need to obtain the populations of the dressed states. We know that the dressed states are coupled by transitions. If you have the upper and the lower dressed states and can do transitions between them, eventually you reach equilibrium, where the populations are then given by the rate equations.
These rate equations can be written down by inspection:
and similarly for . The time derivatives are zero in steady state, such that
Perspective
Why do we treat the scattered spectrum in such detail here? In part, this is because historically the answer to the scattered spectrum question was something all atomic physicists were expected to know. Today, the methods used are particularly important for what we'll do next. When we discuss light forces in the dressed atom picture, we will need to know how many atoms are in each of the dressed states. This example illustrates how the solution of the two-level system gives you complete answers for such population equations.
Note that there are relaxation rates involved. The actual rate equation looks more like
where the relaxation rate goes as . We shall not solve these in detail here, but in principle such rate equations can be solved, and will be useful for later treatments of scenarios such as laser cooling with blue detuned light.
Peak widths
How does the spectrum evolve from strong excitation to weak excitation? At intensities low compared with saturation, the central peak grows; that is the "coherent peak" due to the weak excitation scattering. As the saturation parameter goes to zero, the fraction of coherent emission grows to become all of the emission.
What are the widths of the three lines? The central feature width is . You can take the rate equations and show that the natural relaxation rates give rise to this width. You can also show how this rate originates from the relative relaxation of the sidebands. But more interestingly, perhaps, you can see how they come from the optical Bloch equations. Recall that these equations are a linear three by three matrix equation, where the transition matrix has certain eigenvalues . There are several regimes of interest:
In the weak excitation limit, recall that the relaxation rates of the Bloch vector along the , , and components are , , and . In the limit of , the eigenvalues are , , and . In the high intensity limit, with and , the dressed atom picture provides the intuition that the Bloch vector is strongly rotated about the axis, so the vector spends half its time along , and half its time along , so its damping rate is the average of and , giving the net damping rate . The axis rate is similar. And the axis average rate is .
Diagramatic approach to high intensity excitation limit
We have now appreciated that any process which results in an emitted spectrum which is not a delta function must be a higher order process. Consider, therefore, the perturbative diagram responsible for the upper and lower sideband emissions:
The inelastic component of the central peak, its broad pedestal, comes from the following process: a photon is emitteed from the excited state, then re-absorbed, with the atom resulting back in the excited state, in a process known as "inverse scattering" from .
Radiative cascade
The radiative cascade is an important concept to understand in the dressed atom picture, for conceptual understanding of laser cooling in the dressed atom picture. We consider it in the uncoupled and dressed state basis.
Uncoupled basis
Consider the diagrams which describe the process of an atom absorbing and emitting a photon:
When an excited atom emits a photon, it cannot emit another photon for some time, given by the inverse Rabi frequency. This gives rise to an anti-bunched spectrum, and also points out the fact that on such short timescales the sidebands of the Mollow triplet cannot be observed.
Dressed atom basis
In the dressed atom basis, each time a photon is emitted, we have converted a photon in our special mode into an excitation in one of the dressed atom manifolds. From the upper dressed state, it can emit either on the carrier, or one of the sidebands, but not the other. Many carrier photons can thus be emitted between sideband photons, but the sideband photons emitted must alternate.
References
- see API Chapter VI – worth reading!
Dipole forces within the dressed atom approach
In this section, we visit the physics of stimulated light forces, using the the dressed atom picture. Just to whet your appetite for the following - we will understand, below, why it is blue detuned light you choose for laser cooling at high intensities, rather than red detuned light. Also, recall that in the case of the stimulated force, fluctuations of the stimulated force cause heating. There is a special nature to the fluctuations of the stimulated force, due to the radiative cascade picture in the dressed atom approach. In switching from one dressed level to the next, the force switches sign! The atom thus get kicked back and forth. We will therefore see how these fluctuations of the stimulated force lead to momentum diffusion. The stimulated force has application mostly to dipole traps and optical lattices. Understanding the cooling and heating due to the stimulated force really broadens your understanding of what light forces are about. It is essentially different from the spontaneous light force, involved in the optical molasses.
The insights from this section cover dipole traps, blue molasses, heating from dipole forces, the electromagnetic origin of the dipole forces, and energy conservation.
Review of the dressed atom picture
Let us begin with a reminder about three things we need from the dressed atom picture: energy levels, populations, and relaxation times.
Energies
Recall that there is a splitting between dressed states, giving the energies
Populations
We also want to know the populations and of the dressed states and ; these came from diagonalizing the coupling matrices and introducing rate equations, giving
where .
Relaxation rates
Finally, recall that if we are not in steady state, there are relaxation rates involved which drive the system to the steady state. These rates are proportional to the spontaneous emission rate:
Mean dipole force at zero velocity
Let us begin by considering what force is seen by an atom in a tightly focused laser beam, when the light is detuned to the red or to the blue of the atomic transition.
The dipole force
If you have a laser beam which is spatially focused, then the energy of the atom as a function of position is a function of where the atom is located relative to the beam:
Assume the light is intense, so that we may use the dressed atom picture. The splitting of the energies of the upper and lower dressed level leads to energies , so the forces seen by the upper and lower levels are
Note that in these expressions, the Rabi frequency is a function of space, because of the spatial dependence of the light intensity. The average force is thus
Note that this is only valid in several limits, imposed by the basic constraint that the dressed atom picture is valid (ie strong light intensity).
Dipole forces seen with blue and red detuned light
We may compare what happens when we have blue detuned light versus red detuned light. Consider two choices. What we couple with the light is the ground state with photons, , and the excited state, with photons, . Which of these two states have higher energy for positive (blue) detuning? The state, because the photon has more energy than the atomic transition. Therefore, the proper labels on the energy levels when blue detuned are:
On the other hand, when red detuned, the energy levels should be labeled as:
Keep in mind, however, that spontaneous emission drives the atom towards its ground state. Eventually, therefore, in the blue detuned state the upper energy level eventually has more population, whereas when red detuned the lower energy level has more population.
The dipole force is repulsive for blue detuning, and the dipole force is attractive for red detuning.
What happens when we are on resonance, and the detuning is zero? In this case, the upper and lower states see equal force, so the average force is zero.
Mean dipole force at non-zero velocity
As a second application, let us discuss the mean dipole force seen by an atom which is not at rest, but is slowly moving. This will let us understand how blue detuned light cools an atom, in the dressed atom picture.
We have to go one step beyond what we did for the mean forces, because the derivations above stem from a picture of forces arising from a potential, and motion in a potential is conservative. Recall that the average force is
Now factor in the fact that the populations are not {\em instantaneously} in the steady state, but rather, there is a time lag of before the populations come into equilibrium.
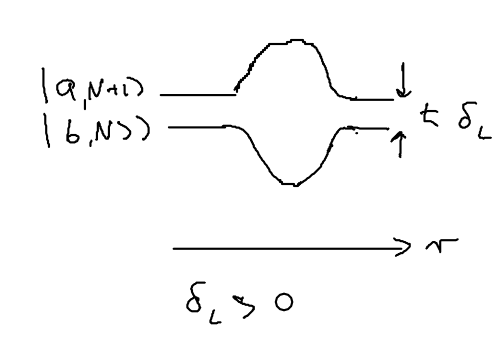
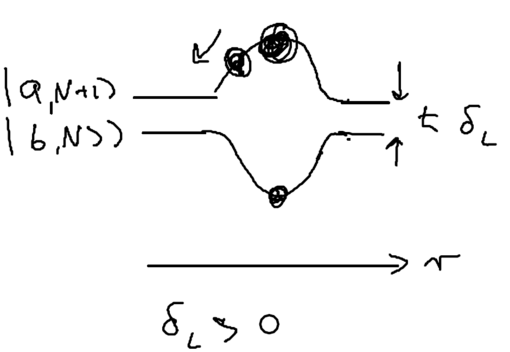
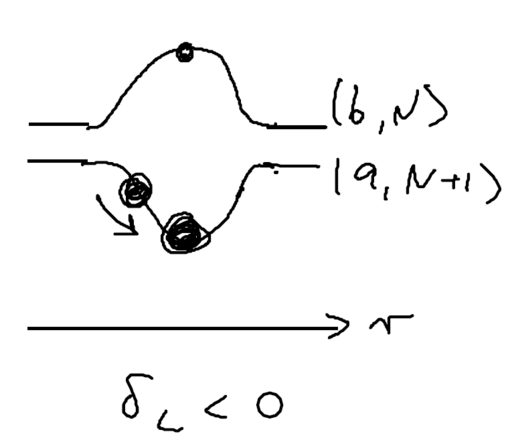
Consider the picture of an atom going through a laser beam; note that this could be a standing wave, as in an optical lattice. Let's figure out what the atom has to do as it traverses the beam. Originally, the atom is purely in the ground state, and at positive detuning the ground state is the upper energy level. To reach the top of the energy hump, there must be some admixture of the excited state added:
The size of the blobs in this picture reflect the population in the level. Assume the atom is moving towards the right. What is the extra force seen because the populations lag behind that which it should have in steady state, as the atom is moving? The more the population is in the upper level, the more force there is to the left. So if the actual population (dotted red lines) is larger than the steady state (solid lines) there is an extra force to the left.
As the atom leaves the middle of the beam, the populations continue to lag behind. But due to the population lag, the upper level population is a bit smaller than it would be in steady state. This causes the atoms to continue seeing a force to the left.
Now imaging that an atom rides a standing wave, going up and down. Because of the time lag in the population, the atoms now see a force in the opposite direction from its movement. Let us emphasize this point: the time lag leads to a hysteresis, which gives rise to dissipation.
More formally, the populations are the steady state values, but not at the present position of the atom, but rather, at a time given by time before:
Thus, the dipole force as a function of position and velocity is
where is the force at , and is the friction coefficient obtained.
Now suppose the light is a one-dimensional standing wave . Averaging over one cycle of the standing wave, we find that the force seen by the atom is
noting that averages to zero.
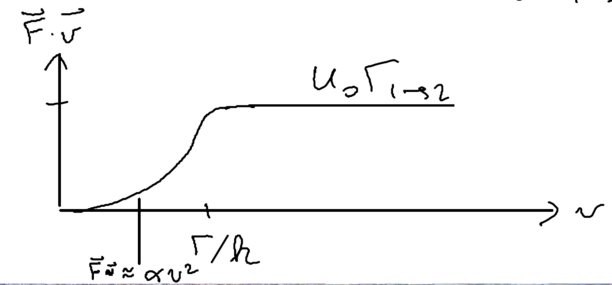
Some limits of this behavior are very useful. In the limit of large detuning , in the standing wave case, we note that , so the friction coefficient in this situation is approximately
This will be derived later, when we strip the dressed atom picture to its bare bones and look at it for physical insight.
Atomic momentum diffusion in the dressed atom picture
We've understood that the dynamics of the radiative cascade leads to population lag, which leads to dissipation. The next thing we want to discuss is that there is also a heating mechanism, which is due to fluctuating forces. Let us see how this arises in the dressed atom picture, for an atom in a standing wave.
Momentum diffusion from force fluctuations
Recall that in the molasses the final temperature was given by , where was the friction force describing how well we cool, and was the momentum diffusion rate due to spontaneous emission. The momentum diffusion coefficient is
Note that such diffusion arises from fluctuating forces. Physically, the momentum is the time integral of all the forces which have been acting on the particle. We can write as . Thus,
Thus, the momentum diffusion coefficient can be written as an integral over the force correlations:
When we discussed momentum diffusion from absorbed light, we had a clear picture of where randomness of momentum came from: the absorbed photons. In this case, we don't have such a clear picture in the absorbed momentum, but we have a clear picture of the forces experienced by the atom. It this thus useful to relate momentum diffusion to the randomness of forces experienced. We will then get a heating rate from
and the final temperature will come from .
Momentum diffusion in the dressed atom picture
In the radiative cascade picture, as the atom cascades through the dressed levels, it experiences a force which is the same in magnitude, but reverses direction from left to right. Thus, we want to write down a statistical average over these fluctuating forces to get the momentum diffusion rate we want.
On resonance, the correlation time, the time range over which forces at time is related to the force at time , is . Thus, the integral we have for the momentum diffusion coefficient should only go over this time period. It means we have that the momentum diffusion rate due to dipole forces is
This is the momentum diffusion rate due to the simulated light force, on resonance.
Away from resonance, the correlation time changes, and there are additional complications, but the basic physics stay the same (see JOSAB paper). The result for arbitrary detuning is
Atoms moving in a standing wave: Sisyphus cooling
The stimulated force is a force which we can fully understand with the two-level atom. It is conceptually simple, and we have analytical expressions for the forces and energy levels. Now let us see what happens when the velocity is not just infinitesimal, but is very large. Instead of just a time lag, the atom is now pictured as flying like a roller coaster. This picture will let us see a cooling mechanism known as sisyphus cooling, that is in practice important. In practice, the multi-level nature of real atoms leads to stronger cooling than expected for two levels, but we can see the necessary insight for this mechanism with sisyphus cooling of two-level atoms.
Let us take the atom velocity to satisfy
meaning that the atom moves through several optical wavelengths within its spontaneous emission lifetime.
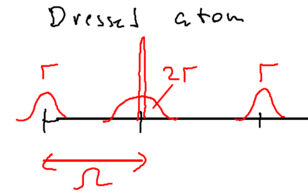
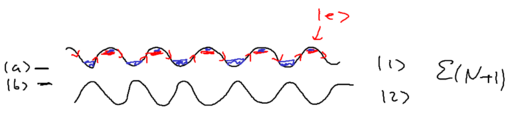
The nice thing about the dressed atom picture is that you can show wonderful drawings and diagrams, so let us draw a nice picture of a standing wave and show it for the manifold of dressed atom levels and within What happens is that the standing wave modulates the energy of the atom in the two dressed states:
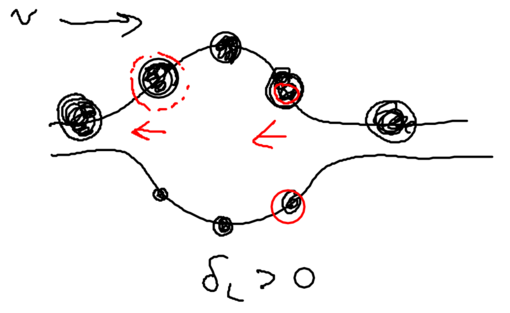
We assume that when we have no light, the ground state (, or ) is the upper sate, and the excited state (, or ) is the lower state. Suppose we start from the left, in this picture, and we go along the standing wave with the atom, which starts in its ground state. Where will the atom emit a photon, with highest probability, switching to the lower state through the radiative cascade? Will this happen at a node, or at an anti-node of the standing wave? The atom has the largest excited state admixture in the anti-nodes of the standing wave, so it is there where the atom emits.
So where the atom end up after emitting a photon? It can end in an upper state, at which point nothing changes with respect to forces on it, since it has stayed in the same dressed level. More interesting is what happens when the radiative cascade leads the atom to the lower dressed level:
When an atom ends up in the lower dressed level, when is it most likely to emit the next photon? The lower level is correlated with the excited state, so when there is no light, it atom is purely in its excited state. As it enters an anti-node, the atom evolves into a superposition of the excited and ground states. So it is most likely to emit when it is purely in the dark, meaning where the splitting of states is minimal.
This happens at the top of the hill. Thus, the physical picture is
that the atom has to climb up a potential hill again whereupon it can
once again emit a photon. In Greek mythology, King Sisyphus did
something bad, so he had to roll a stone up a hill, and when it
reached the top it fell down again, and he then had to roll it up the
hill again. This is what happens with the atoms in this standing
wave: it continuously climbs a hill.
The result we have is that for both dressed states and , we have a preferential spontaneous emission at the top of the hill. This implies cooling, at the rate proportional to
where is the kinetic energy difference between the top and bottom of the standing wave potential hill. is the rate of the switching between sidebands of the radiative cascade.
Experimental implementation
For more about Sisyphus cooling, see the book by Metcalf and van der Straten, and the descriptions of experiments therein.
The first experiment did laser cooling of an atomic beam, and showed that with a blue detuned standing wave the beam velocity distribution narrowed (cooling the atoms), and with a red detuned standing wave it broadened (heating the atoms).
Dressed atoms in a perturbative limit: cooling in a standing wave
Let us now use the dressed atom picture to give, in the simplest limit (a perturbative limit), a summary of concepts of laser cooling in a standing wave. We take , neglect factors of the order of unity, and take .
If we have a standing wave,
the two dressed levels are, to leading order,
These simple expressions give us the transition rate from to ,
since the atom must start in the excited state and end up in the ground state. The transition rate from to is just
in this perturbative limit.
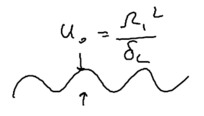
The energy of the dressed states change in the standing wave, giving us what we can call the "dressed state potential," which is physically nothing more than the AC stark shift
with potential height .
In this picture, we can go back to look at Sisyphus cooling once more, staring with the assumption , but relaxing this to look at intermediate velocities. The cooling rate is (note that which happens much faster and thus is not limiting). When the velocity of that atom is much smaller, it cannot climb up and down many hills. But we know that the friction force is linear, so we expect what we have in intermediate velocity regimes is that there is some energy loss rate :
Using the model that we have an initial parabola followed by a straight line, we obtain an estimate for the friction force
Thus, we find very nicely that the perturbative approach gives all the essential physics of what we derived above in a more rigorous manner.
Diffusion
It turns out that the limit of cooling is always higher than the depth of the optical lattice, and to understand this we need to return to the diffusion coefficient. Building on our perturbative expressions, recalling that
we may use the fact that the atoms are mainly in state . The interesting situation is when the atoms are on the slope of the standing wave, where . For a duration , at rate , the atom jumps and the force also jumps, to the opposite value .
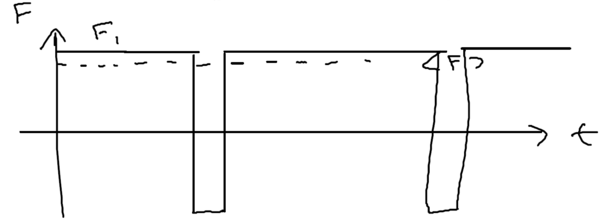
Graphically, we may see what happens by plotting the force seen by a typical atom as a function of time:
In the initial dressed level, the atom sees a constant force, then emits a photon, going to the other dressed level (essentially the excited state) for a short time , before returning. The dominant contribution to the fluctuation in the force comes from these brief spikes, so the momentum diffusion coefficient can be written down by inspection as
where the expression on the right is the probability that the atom is in state , in our picture.
Plugging in numbers, we get
The ultimate temperature limit achievable from this cooling is thus
This means that, according to the perturbative approach, there is competition between cooling and heating, resulting in a minimum temperature set by the depth of the lattice. Keep in mind that cooling to zero temperature cannot be accomplished either, using this mechanism, since the analysis assumes that . Two-level atoms therefore cannot be localized in an optical lattice by stimulated laser cooling. The only reason why localization of atoms in a lattice is possible is through other mechanisms, such as polarization gradient cooling.
Physics of the dipole force
Four physical pictures of the dipole force
Let us recall four different physical pictures for deriving the dipole force:
- Optical Bloch equations.
- Dressed atom picture.
- Classical dipole model of atom, in electric field.
- Macroscopic dielectric object.
Classical dipole
The classical dipole model is based on the fact that the force seen by the dipole depends on whether the electric dipole is in-phase or out-of-phase with the driving field . This gives either an attractive or repulsive force.
Macroscopic dielectric object
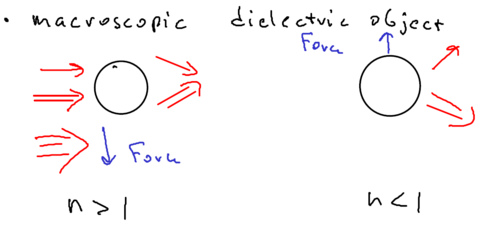
The picture of a macroscopic dielectric object assumes, for example, that you have a microscopic sphere of glass, with a laser beam which is stronger in part of space than another:
So if the microsphere were an atom, with index of refraction greater than one, then the sphere moves toward the field maximum. This is because if you imagine the microsphere is a prism (with index greater than one), then the upper beam is deflected downwards and the lower beam is deflected upwards, such that the sphere acts like a lens. The sphere then is forced to move to compensate for the imbalance in the change of photon momentum of the two refracted beams.
Optical tweezers have made an impact on biology almost as large as the impact of laser cooling on atomic physics. With optical tweezers, one can now manipulate objects within a cell. The people who demonstrated optical tweezers first were the same people who demonstrated laser cooling first: Art Ashkin, who teamed up with Steven Chu, at Bell Labs, in the late 1980's.
Electric and magnetic components of the dipole force
Now a question. We have discussed the stimulated light force, also called the dipole force, or the reactive force. Is this force an {\em electric} force (the force on an electric dipole), a magnetic force (Lorentz force), or both? In other words, imagine an atom is in the potential of the standing wave in an optical lattice. Is the potential due to electric forces or magnetic forces? Intuition says that the force is electric, because the electric force is generally larger than the magnetic one. However, that turns out to be incorrect, and indeed it is the Lorentz force which gives rise to the electric dipole potential. At this point, you may completely appreciate the electric dipole potential, since by writing you actually include magnetic forces.
Static fields
In the limit of DC fields, everything does have to be electric, so let us begin with electrostatics. Consider two charges separated by distance :
The energy of this configuration is , due to the polarizability of the atom. Now imagine the charge is placed in an inhomogeneous field:
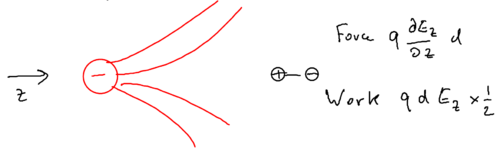
There is a force on the two halves of the dipole, and the two would cancel unless there is a gradient, so the force on the dipole is
so the work done is
When we move the dipole not along the electric field, but rather, perpendicular to the electric field, consider what happens:
Now, what is the force on the dipole? What matters is the component of the force, which is caused by the component of the electric field, or more specifically, it matters that the component changes by the distance separating the two charges in the dipole.
Now, we want to use the fact that in electrostatics, the curl of the electric field is zero, and therefore by vector calculus,
and the work done by moving the dipole in from infinity is . This derivation relied on there being no magnetic fields, because otherwise the curl of the electric field would not be zero.
Oscillating fields
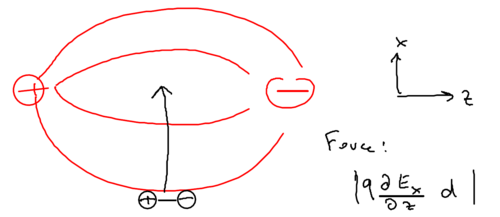
Now consider an oscillating dipole in a standing wave, created by counter-propagating laser fields, so that the electric field is perpendicular:
Recall that the potential from the AC Stark shift is . Let us understand what the force is, which provides this periodic potential. Well, if you have a plane standing wave, that means you can draw the above picture extended up and down. What is the electric force on the dipole in that case? The dipole moment and the gradient of the electric field are orthogonal, in this configuration. There is thus no gradient in the field along the direction of the dipole. Thus, in a plane standing wave, the electric force is identically zero, . So where does the force come from?
It must originate from the Lorentz force. In this scenario, recall that the Lorentz force is . There is an oscillating dipole in the scenario. If you take the derivative of the optical dipole potential, the Lorentz force is
The standing wave has both electric and magnetic components,
The dipole potential, averaged over a cycle, is
Recall that the dipole moment is . Thus, the Lorentz force is
Inserting the expression above for the electric field, we thus obtain this expression for the Lorentz force:
Now averaging, we find
where we now recognize the term on the right in the parentheses as the dipole potential.
Thus, we see that the stimulated force can be either electrical, that is of the form , or magnetic, that is, of the form , in nature. Each of the two forces may not be curl free, but the sum of both can be.
Energy conservation and dipole forces
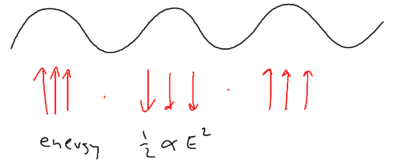
When we considered the dipole force earlier, we looked at how it arises from a redistribution of photons. If you have a monochromatic array of beams, the dipole does not arise due to spontaneous emission, but rather, because photons are taken from one beam and put into another beam. So how can this result in a change of energy for the atom?
Energy conservation in blue molasses picture
Well, energy exchange does occur, because as we saw atoms flying along a blue standing wave, in the picture of "blue molasses," sees a damping force as it walks up the potential hills:
When atoms slow down due to this viscous force, where has the kinetic energy of the atoms gone?
If you have an ordinary molasses, the energy is radiated away. The basic ingredients available, therefore, are photon absorption, stimulated emission, and spontaneous emission. Recall that in Sisyphus cooling, an atom does emit a photon after climbing up a hill. From the upper dressed level, it emits a blue detuned photon, when the sideband splitting is larger. From the lower dressed level, it emits at the top of the potential, at which the sideband splitting is smaller. The upper sideband is emitted at a larger Rabi frequency than the lower sideband.
The principle behind this observation is that spontaneous emission is once again responsible for the removal of entropy involved in the laser cooling process, and energy is removed along with the entropy change.
One way for providing dissipation is thus radiation into the sidebands.
Transient energy conservation picture
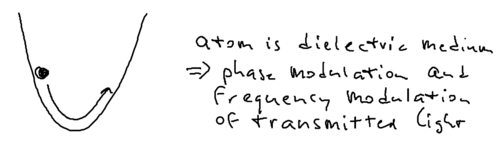
Another scenario for understanding energy conservation is the following transient experiment. Imagine that you have an atom in the harmonic potential of an optical dipole trap.
In extremely far detuned optical lattices, there is essentially no spontaneous emission. The atom oscillating in the dipole trap, say at 1 Hz, going from high to low energy. It is clear this energy must be transformed into the light field, and the question is what actually happens. But it turns out the energy does not emit through spontaneous emission.
What happens is that the moment the atoms reach the bottom of the trap, they have a maximum in energy. The photons which pass through the atom at that point are red shifted. When the atom climbs up the potential hill, the photons are blue shifted. While the atom oscillates, the photons which arrive are blue and red shifted. There is no spontaneous emission in this transient picture, but there is phase modulation of the laser which shifts the laser frequencies.
In principle, this frequency shift should be observable in an experiment. In practice, this is complicated by the fact that real experiments involve spatially inhomogeneous beams, so there is some momentum change as well as phase change of photons involved.
References
- Important paper: J. Dalibard and C. Cohen-Tannoudji, J. Opt. Soc. Am .B 2, 1707 (1985) Download











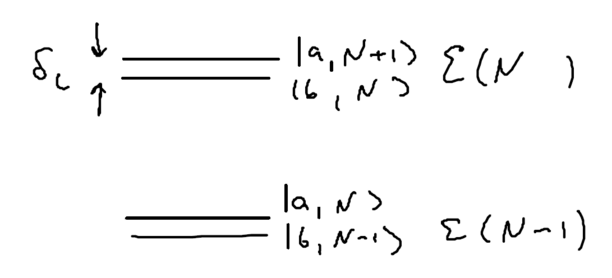
















![{\displaystyle {\frac {\hbar }{2}}\left[{\begin{array}{cc}{-\delta _{L}}&{\Omega _{1}}\\{\Omega _{1}}&{\delta _{L}}\end{array}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/369cacb5e96c19a15ae6d6300d6b1e433c72d28b)