imported>Ichuang |
imported>Ichuang |
| (6 intermediate revisions by the same user not shown) |
| Line 7: |
Line 7: |
| | * Magneto-Optical Traps | | * Magneto-Optical Traps |
| | | | |
| − | == The spontaneous light force == | + | == Optical Molasses == |
| − | Consider a two-level atom with energy spacing <math>\omega_0</math>,
| |
| − | interacting with a single mode laser beam:
| |
| − | ::[[Image:chapter1-intro-to-cooling-Lec1-twolevel.png|thumb|408px|none|]]
| |
| − | Let the laser intensity be <math>I</math>, and the interaction matrix element
| |
| − | between atom and light be <math>\hbar\omega_R = \vec{E}\cdot
| |
| − | | \langle 1|e\vec{r}|2{\rangle}|</math>, where <math>\omega_R</math> is known as the Rabi frequency,
| |
| − | <math>\vec{E}</math> is the electric field strength, and <math>e\vec{r}</math> is the dipole
| |
| − | moment of the atom.
| |
| | | | |
| − | It is useful to define a quantity known as the saturation intensity
| + | {{:Optical Molasses}} |
| − | <math>I_0</math> as the intensity of light at which the rabi frequency becomes
| |
| − | <math>\omega_R = \Gamma/\sqrt{2}</math>, where <math>\Gamma</math> is the spontaneous
| |
| − | emission rate (the natural decay rate of the atom from <math>|2{\rangle}</math> to
| |
| − | <math>|1{\rangle}</math>, excited to ground state). This gives
| |
| − | :<math>
| |
| − | \frac{I}{I_0} = \frac{2\omega_R^2}{\Gamma^2}
| |
| − | \,.
| |
| − | </math>
| |
| − | The rate at which photons are scattered from the atom is known to be
| |
| − | :<math> | |
| − | \gamma_s = \frac{\Gamma}{2} \frac{I/I_0}{1+\frac{I}{I_0} +
| |
| − | (2\delta/\Gamma)^2}
| |
| − | \,,
| |
| − |
| |
| − | </math>
| |
| − | where <math>\delta</math> is the frequency detuning of the laser from the center
| |
| − | of resonance of the atom. Two useful limits of this scattering rate
| |
| − | are
| |
| − | :<math>\begin{array}{rcl}
| |
| − | \lim_{I\rightarrow\infty} \gamma_s &=& \frac{\Gamma}{2}
| |
| − | = \frac{1}{2\tau}
| |
| − | \\
| |
| − | \lim_{I\rightarrow I_0} \gamma_s &=& \frac{\Gamma}{4}
| |
| − | \,,
| |
| − | \end{array}</math>
| |
| − | where we have assumed <math>\delta=0</math> (resonant light). These expressions
| |
| − | have a natural physical interpretation: in the limit of infinite
| |
| − | intensity, the atomic levels become equally populated between the
| |
| − | excited and ground state, and thus only half the atoms (the excited
| |
| − | ones) can scatter light. Thus, the scattering rate is <math>\Gamma/2</math> in
| |
| − | that limit.
| |
| | | | |
| − | Suppose the force imparted by light on the atom is given by the recoil
| |
| − | of photons spontaneously emitted from the atom. This force would then
| |
| − | be
| |
| − | :<math>
| |
| − | F = \hbar k \gamma_s
| |
| − | \,,
| |
| − | </math>
| |
| − | where <math>\hbar k</math> is the momentum of each photon. This expression makes
| |
| − | several assumptions: that is is the net momentum transfer in absorption,
| |
| − | that there is no "stimulated" force, and that <math>\hbar k/m k \ll
| |
| − | \Gamma</math>, meaning that the jump in the Doppler shift is less than the
| |
| − | natural linewidth.
| |
| − |
| |
| − | Typically, for alkali atoms, this force is <math>F\leq 10^5 g</math> times the
| |
| − | mass of an atom (<math>g</math> being the acceleration due to gravity). This
| |
| − | means that light can stop a sodium atom going at <math>1000</math> m/s in one
| |
| − | millisecond, or about half a meter. In comparison to electrostatic
| |
| − | forces on ions, this is very small, however: it is comparable to the
| |
| − | force exerted by an electric field of 1 millivolt/cm on an ionized
| |
| − | sodium atom.
| |
| − |
| |
| − | Moving atoms experience a Doppler shift, which we can model as a
| |
| − | frequency dependent force, based on Eq.(\ref{eq:ci:lorentzian}), as
| |
| − | :<math>
| |
| − | F = \hbar k \frac{\Gamma}{2} \frac{I/I_0}{1+\frac{I}{I_0} +
| |
| − | 2\left[\frac{(2\delta+kv)}{\Gamma}\right]^2}
| |
| − | \,,
| |
| − |
| |
| − | </math>
| |
| − | where <math>v</math> is the velocity of the atom. The effect of a fixed laser
| |
| − | frequency on an ensemble of atoms is to modify their Maxwell-Boltzmann
| |
| − | thermal velocity distribution:
| |
| − | ::[[Image:chapter1-intro-to-cooling-l1fig2.png|thumb|408px|none|]]
| |
| − | Note how the initial distribution changes to one with atoms piling up
| |
| − | below the velocity group resonant with the laser. The atoms bunch.
| |
| − | Historically, this is the first method that was done to cool atoms to
| |
| − | Kelvin temperatures.
| |
| − |
| |
| − | == One-dimensional optical molasses ==
| |
| − | Let us now turn to a method which allows cooling of atoms to zero
| |
| − | velocity. Consider two laser beams incident on an atom from opposite
| |
| − | directions. We assume that the total force is the sum of the two
| |
| − | forces, ignore standing wave effects, and take the laser intensity to
| |
| − | be low compared with the saturation intensity, <math>I\ll I_0</math>. Taking the
| |
| − | force to be the sum of two forces described by Eq.(\ref{eq:ci:vdf}),
| |
| − | we find that the two lorentzians sum to give the following force as a
| |
| − | function of velocity:
| |
| − |
| |
| − | ::[[Image:20090410-094308_light-force-fig2.png|thumb|500px|none|]]
| |
| − | The velocity dependent force is positive from one light beam, and
| |
| − | negative from the other. With a detuning chosen such that force is
| |
| − | zero at zero velocity, the force around <math>v=0</math> can be expanded
| |
| − | linearly, giving
| |
| − | :<math>
| |
| − | F(v) = -\alpha v
| |
| − | \,,
| |
| − | </math>
| |
| − | where <math>\alpha</math> describes the viscosity imparted by the light
| |
| − | force to the atom, reflecting the restoring force applied when the
| |
| − | atom is not at zero velocity. This configuration is known as an {\em
| |
| − | optical molasses}, because of this restoring force, which makes the
| |
| − | light behave like a thick, viscous medium for the atoms in it.
| |
| − | The damping coefficient <math>\alpha</math> can be calculated to be
| |
| − | :<math>
| |
| − | \alpha = 2\hbar k^2
| |
| − | \frac{(2I/I_0)(2\delta/\Gamma)}{\left(1+\left(\frac{2\delta}{\Gamma}\right)^2\right)^2}
| |
| − | \,.
| |
| − | </math>
| |
| − |
| |
| − | == The Doppler cooling limit ==
| |
| − | We have seen that the spontaneous light force, characterized by the
| |
| − | Lorentzian response of an atom to light, together with the Doppler
| |
| − | shift due to movement of the atom, gives a velocity dependent force,
| |
| − | which can be zero at zero velocity. Does this mean that the atoms can
| |
| − | be cooled to zero temperature?
| |
| − | If the rate of energy loss due to cooling is
| |
| − | :<math>
| |
| − | \dot{E}_{\rm cool} = F v = -\alpha v^2 = -\frac{2\alpha}{M} E
| |
| − | \,,
| |
| − | </math>
| |
| − | then we should reach zero velocity, and zero temperature. Indeed, the
| |
| − | kinetic energy decays exponentially. However, the spontaneous force
| |
| − | has a random character, and thus has fluctuations which limit the
| |
| − | minimum temperature achievable.
| |
| − | This limit is determined by momentum diffusion. The force imparted
| |
| − | can be described by a random walk. The final momentum is
| |
| − | :<math>
| |
| − | p_{\rm final}^{RMS} = \hbar k \sqrt{N}
| |
| − | \,,
| |
| − | </math>
| |
| − | on average, due to the random walk. Note that the momentum spread is
| |
| − | :<math>\begin{array}{rcl}
| |
| − | \langle p^2 \rangle &=& (\hbar k)^2 v
| |
| − | \\
| |
| − | \frac{d \langle p^2{\rangle}}{dt} &=& (\hbar k)^2 \gamma_s
| |
| − | \,.
| |
| − | \end{array}</math>
| |
| − | This describes heating which arises due to photons randomly scattering
| |
| − | in all directions, such that the net momentum almost adds up to zero,
| |
| − | but not quite. There is also a similar term due to absorption: some
| |
| − | atoms will absorb more or less photons, due to the Poissonian
| |
| − | statistics of absorption.
| |
| − | Thus, the time variation of the kinetic energy due to the fluctuating
| |
| − | forces is
| |
| − | :<math>
| |
| − | \dot{E}_{\rm heat} = \frac{2\hbar^2 k^2\gamma_s}{2M} = \frac{D}{M}
| |
| − | \,,
| |
| − | </math>
| |
| − | where <math>D</math> is the momentum diffusion coefficient
| |
| − | :<math>
| |
| − | D = \frac{ \langle p^2{\rangle}}{2}
| |
| − | \,,
| |
| − | </math>
| |
| − | which we'll later see is a correlation function of the fluctuation
| |
| − | forces.
| |
| − | Let us now derive the Doppler limit for cooling. In equilibrium,
| |
| − | <math>\dot{E}_{heat} = \dot{E}_{cool}</math>. This means
| |
| − | :<math>
| |
| − | \frac{D}{M} = \frac{2\alpha}{M}E
| |
| − | \,.
| |
| − | </math>
| |
| − | The heating rate is independent of kinetic energy, whereas the cooling
| |
| − | rate is a function of kinetic energy. So as the atoms cool down, the
| |
| − | cooling rate slows down, resulting in a final temperature equilibrium
| |
| − | being reached:
| |
| − | :<math>
| |
| − | 2E_{final} = kT_{\rm doppler} = \frac{D}{\alpha}
| |
| − | </math>
| |
| − | <math>\alpha</math> is a viscosity parameter: it reflects transport. <math>D</math>
| |
| − | reflects mobility. Thus, this is an Einstein relation, a universal
| |
| − | expression in statistical mechanics resulting from the fundamental
| |
| − | theorem which relates dissipation to fluctuations.
| |
| − | We've now obtained an expression for the Doppler limit temperature, a
| |
| − | limit on the temperature an ideal two-level atom can be cooled to by
| |
| − | laser beams,
| |
| − | :<math>
| |
| − | k T_{\rm doppler} = \frac{\hbar\Gamma}{2}
| |
| − | \,.
| |
| − | </math>
| |
| − | This optimal temperature is achieved for <math>I\ll I_0</math>, and detuning of
| |
| − | <math>\delta = -\Gamma/2</math> (half a linewidth). Physically, at low
| |
| − | temperatures, the atom cannot determine whether the photon comes from
| |
| − | left or right; at higher temperatures, the atom can discriminate
| |
| − | whether photons come from left or right, thus cooling. For sodium,
| |
| − | this temperature is <math>240</math> <math>\mu</math>K, corresponding to a velocity of <math>30</math>
| |
| − | cm/s.
| |
| | == Beam slowing == | | == Beam slowing == |
| | | | |
| − | We have previously looked at cooling with two laser beams, focusing on
| + | {{:Beam Slowing}} |
| − | the idea that if you want to cool, you need a force which is linear
| |
| − | with velocity. Now, let us see how you can cool with a single laser
| |
| − | beam. That is what you do when you have a single atomic beam. With a
| |
| − | single laser beam, you can not only slow them down, but also bunch
| |
| − | them up, obtaining the same velocity distribution you get with a
| |
| − | molassas. This is the only example of laser cooling I know of which
| |
| − | has a very simple, closed form solution, which is possible because
| |
| − | there is only one laser beam.
| |
| − | | |
| − | Imagine, if you have a single Lorentzian, how can you cool?
| |
| − | Generically, you need a ``lock'' point, which is stable and has atoms
| |
| − | moving to that point in phase space from either velocity direction.
| |
| − | With a single beam you don't apparently have such, but as we shall see
| |
| − | there is something else interesting that can be done.
| |
| − | | |
| − | Consider a single beam of atoms, with this velocity distribution.
| |
| − | Using a laser, you can push some of the atoms to become cooler (red
| |
| − | line below), bunching them up in a lower velocity regime, and leaving
| |
| − | atoms faster than some velocity unchanged. What do you have to do if
| |
| − | you want to bunch all the atoms at zero velocity? It becomes clear
| |
| − | that you want more than one laser frequency, for example. By applying
| |
| − | a broad range of frequencies which cover the whole velocity
| |
| − | distribution, you can slow down all the atoms. There are several
| |
| − | techniques using such an approach, known as white light slowing, or
| |
| − | diffuse light slowing. But none of those are as powerful as
| |
| − | {\em chirpedd slowing} and {\em Zeeman slowing}, the techniques of choice | |
| − | in modener laser cooling.
| |
| − | | |
| − | <!--
| |
| − | Let us now go back to slowing and atomic beams, in which we have many
| |
| − | atoms and only one laser beam. If we have a Maxwell-Boltzmann
| |
| − | distribution with atoms moving counterpropagating to the laser, the
| |
| − | atoms' velocity distribution is pushed to lower velocities:
| |
| − | ::[[Image:chapter1-intro-to-cooling-Lec1-beam-slowing.png|thumb|612px|none|]] | |
| − | Note that in the Doppler cooling picture, we can only talk to atoms
| |
| − | which are already pretty slow. From an atomic beam, however, there
| |
| − | are hardly any atoms within this capture velocity range. It would be
| |
| − | much nicer to collect atoms from the whole MB distribution; this is
| |
| − | called beam slowing. Two stages are typically used: beam slowing,
| |
| − | then Doppler cooling.
| |
| − | | |
| − | We studied Doppler cooling first, because it was useful to get the
| |
| − | concepts of the friction force and momentum diffusion.
| |
| − | Beam slowing uses only one laser beam, but involves an extra twist in | |
| − | that we must first transform into a decelerating frame. Conceptually,
| |
| − | the idea is to change the frequency of light applied as the atoms slow
| |
| − | down, so that atoms continually experience a negative force. One way
| |
| − | to accomplish this is to use multiple laser frequencies (white light
| |
| − | slowing). Another is "diffuse light slowing" which uses light
| |
| − | covering a large spectrum. Most efficient is to use a single
| |
| − | frequency, and change the detuning of atoms with a magnetic field (re
| |
| − | homework). We'll discuss "chirped slowing," because of its
| |
| − | conceptual simplicity. It has little experimental use today, but was
| |
| − | important in the mid 90's.
| |
| − | -->
| |
| − | | |
| − | === Chirped slowing ===
| |
| − | | |
| − | The idea behind chirped slowing is to get the atoms to "ride the surf". In other words, the frequency chirp of the laser beam and the deceleration of the atoms should be synchronized.
| |
| − | | |
| − | ==== Balance of equations ====
| |
| − | | |
| − | ===== Step 1 =====
| |
| − | | |
| − | The force on an atom in the beam due to the light is
| |
| − | :<math>
| |
| − | F = -\hbar k \frac{\Gamma}{2} \frac{I/I_0}{1+I/I_0 + \left[
| |
| − | \frac{2(\delta+k v)}{\Gamma} \right]^2}
| |
| − | </math>
| |
| − | Let <math>a</math> denote the atom's acceleration.
| |
| − | Let us assume a frame of reference and experimental setup such that
| |
| − | <math>a<0</math>, <math>v>0</math>, <math>k>0</math>, <math>a_{max}>0</math>. We can call <math>\hbar k \Gamma/2 = M
| |
| − | a_{max}</math>, where <math>M</math> is the atom's mass.
| |
| − | | |
| − | ===== Step 2 =====
| |
| − | | |
| − | The scheme begins by selecting the deceleration desired, some <math>a<0</math>.
| |
| − | Then set <math>F = -Ma</math>, and look for a <math>\delta' = \delta + kv</math> to obtain
| |
| − | this desired force.
| |
| − | <!-- In particular, we find
| |
| − | :<math>
| |
| − | a = \frac{-I/I_0}{1_I/I_0
| |
| − | </math>
| |
| − | -->
| |
| − | This will exist if
| |
| − | :<math>
| |
| − | |a| < \frac{I/I_0}{1+I/I_0} a_{max}
| |
| − | \,.
| |
| − | </math>
| |
| − | | |
| − | ===== Step 3 =====
| |
| − | Next, select an initial velocity <math>v_0</math> such that <math>v(t) = v_0 + a t</math>.
| |
| − | <math>\delta'</math> is the detuning for this "targeted" velocity group, so we
| |
| − | must provide a laser with frequency in the lab frame of <math>\delta(t) =
| |
| − | \delta' - k v(t)</math>. The atom's velocity will differ from the desired
| |
| − | target group by <math>v' = v-v(t)</math>.
| |
| − | | |
| − | ===== Step 4 =====
| |
| − | | |
| − | With these definitions, we now have
| |
| − | :<math>
| |
| − | F = -\hbar k \frac{\Gamma}{2} \frac{I/I_0}{1+I/I_0 + \left[
| |
| − | \frac{2(\delta'+k v')}{\Gamma} \right]^2}
| |
| − | \,,
| |
| − | </math>
| |
| − | in the frame of reference of the atoms in the target velocity group.
| |
| − | | |
| − | ===== Step 5 =====
| |
| − | | |
| − | Transforming into this decelerating frame, we get a fictitious force
| |
| − | with is <math>F_{fict} = -Ma</math>, and
| |
| − | :<math>
| |
| − | F'(v') = M a_{max} \left[
| |
| − | \frac{I/I_0}{1+I/I_0 + \left[
| |
| − | \frac{2(\delta'+k v')}{\Gamma} \right]^2 }
| |
| − | + \frac{I/I_0}{1+I/I_0 + \left[
| |
| − | \frac{2(\delta')}{\Gamma} \right]^2 }
| |
| − | \right]
| |
| − | </math>
| |
| − | This second term has the same structure as the first, but it is
| |
| − | velocity independent. Note that this is exact, and valid for arbitrary <math>v'</math>. All we've done is to substitute definitions, so far, but they provide useful intuition.
| |
| − | | |
| − | Note that for small <math>v'</math>, this force is linear in velocity, <math>F'(v') = -\alpha v'</math>.
| |
| − | | |
| − | ==== Decelerating Frame ====
| |
| − | | |
| − | In the lab frame, we have a force which is a positive Lorentzian. In
| |
| − | the decelerating frame, we had to add <math>-Ma</math> (the inertial force),
| |
| − | so this Lorentzian shifts down, when we plot the total force as a function of the velocity in the decelerating frame <math>v'</math>:
| |
| − | ::[[Image:chapter1-intro-to-cooling-Lec1-beam-slowing-lock.png|thumb|510px|none|]]
| |
| − | Therefore, there is now a stable "lock" point, where <math>F'=0</math> as a
| |
| − | function of <math>v'</math>. In other words, when the atoms have a negative velocity <math>v'</math>, the atoms all accelerate towards zero velocity (in the decelerating frame). And when atoms have a small positive velocity, they also move towards <math>v'=0</math>. In contrast the point where the Lorentzian has <math>F'(v')=0</math> at <math>v'>0</math>, is unstable.
| |
| − | | |
| − | Thus, we may write, as we did with the molasses, an
| |
| − | expression for the linearized force around this point, <math>F'(v') =
| |
| − | -\alpha v'</math>, in which <math>\alpha_{beam} =
| |
| − | \alpha_{molasses}/2</math>. There is also randomness, as there was in the optical molassas case, for which we may calculate a momentum diffusion
| |
| − | coefficient, and we find that <math>D_{beam} = D_{molasses}/2</math>. Thus,
| |
| − | the final temperature limit of the beam is actually the same as that
| |
| − | achievable with a molasses: <math>kT_{beam} = kT_{molasses}</math>.
| |
| − | | |
| − | | |
| − | We've seen that one laser can bunch up atoms from a beam at a single
| |
| − | velocity. Physically, what happens is that if the atoms fall behind,
| |
| − | the light does not interact with them, but if the atoms are too fast,
| |
| − | the laser cools them, much like in the molasses case.
| |
| − | | |
| − | ==== Graphical summary ====
| |
| − | | |
| − | Here is a graphical summary of what we've learned about beam slowing.
| |
| − | In the decelerating frame, this is the situation. Change sign, so
| |
| − | that in the frame the decelerating force is positive, for this graph:
| |
| − | ::[[Image:chapter1-intro-to-cooling-Lec1-bs-velocity.png|thumb|408px|none|]]
| |
| − | | |
| − | Initially, our zero force point is at the targeted velocity <math>v_0</math>.
| |
| − | All atoms at larger velocity experience a constant positive force,
| |
| − | accelerating them. After a later time <math>t</math>, the tail of the
| |
| − | maxwell-Boltzmann distribution is pushed to higher velocities. The peak of distribution of atoms grows higher and higher with time, while the positive tail moves to higher velocities.
| |
| − | | |
| − | This is the description in the decelerating frame.
| |
| − | | |
| − | In the lab frame, we shift from <math>v'</math> back to <math>v</math>. This means that we just shift all the distributions down in velocity. We start with a broad distribution at <math>t=0</math>. There is a velocity group at <math>t=0</math> which is on resonance with the laser beam. As time goes on, the laser beam chirps, causing more and more atoms to come into resonance, piling them up in a lower velocity class. What happens is that after the laser beam is switched off, you may still have a low velocity tail which is not reached by the laser, but you have a huge peak of atoms that have been cooled:
| |
| − | | |
| − | ::[[Image:chapter1-intro-to-cooling-Lec1-bs-lab-frame.png|thumb|408px|none|]]
| |
| − | | |
| − | All the atoms at lower velocities are pushed up in velocity
| |
| − | until they stack up at <math>v_0</math>, producing a narrow distribution around
| |
| − | <math>v_0</math>.
| |
| − | | |
| − | The width of this narrow velocity distribution is given by <math>k_BT = D/\alpha</math>, which is proportional to
| |
| − | <math>\sqrt{kT_{beam}}/M</math>.
| |
| − | | |
| − | Beam cooling is actually the simplest and cleanest example of laser
| |
| − | cooling. It has the same physics as the molasses case, with the second beam being replaced in a sense by a ficticious force. Note that in the two-beam molasses case, there are more complications, since one should really
| |
| − | consider interference effects.
| |
| − | | |
| − | == Energy conservation in laser cooling ==
| |
| − | | |
| − | === Kinetic energy conservation ===
| |
| − | Where does the lost kinetic energy go, in cooling the atoms? In the beam cooling scenario, for example, you have moved a large number of atoms from high velocities to low velocities. How can this be reconciled with energy conservation? Well, there are only several possibilities for where the energy can go. In particular, there is light scattered by the atoms, and the energy is radiated away by spontaneous emission, as we shall now see.
| |
| − | | |
| − | Absorption is responsible for momentum change, and emission is responsible for energy conservation. Light emitted by the atom is at the resonant energy <math>\omega_0</math>, but
| |
| − | can be absorbed when the photon is just slightly less than <math>\omega_0</math>.
| |
| − | The emission is isotropic, whereas the incident light is directed and
| |
| − | Doppler shift dependent.
| |
| − | ::[[Image:chapter1-intro-to-cooling-Lec1-energy.png|thumb|300px|none|]]
| |
| − | Doppler cooling can be explained in this picture. Incident laser light is
| |
| − | detuned below <math>\omega_0</math> ("red detuned"), whereas emitted photons are, on average, at a higher frequency, so more energy is emitted than is absorbed, when an atom is cooled.
| |
| − | | |
| − | === Energy conservation in general cooling schemes ===
| |
| − | | |
| − | The same intuition can be applied to all cooling schemes, including those used to cool solids and liquids. Phonon
| |
| − | assisted absorption is balanced against emission, resulting in cooling:
| |
| − | ::[[Image:chapter1-intro-to-cooling-Lec1-cooling-solid.png|thumb|450px|none|]]
| |
| − | How hard is it to cool liquids and solids? Consider a system at
| |
| − | <math>T=1</math>K; that gives the phonon energy. Then <math>\hbar\omega = 25,000</math>
| |
| − | Kelvin. In practice, there is a lower than unity fluorescence quantum
| |
| − | yield, because there are non-radiative ways to exit the excited
| |
| − | state. The cooling will be efficient, however, only when the quantum
| |
| − | yield is higher than <math>1-1/25000</math>, which is typically unrealistic.
| |
| − | Cooling with laser light is therefore not typically practical, for
| |
| − | systems other than atoms, which have a unity fluorescence quantum
| |
| − | yield. Molecules are hard, because they have non-radiative
| |
| − | de-excitation pathways.
| |
| − | | |
| − | == 3D molasses, high intensities ==
| |
| − | To cool atoms along not just one axis, but along three axes, use six
| |
| − | counter-propagating laser beams. This configuration is called a 3D
| |
| − | molasses. Everything we've discussed in one dimension can be applied;
| |
| − | just sum up the forces. Some care must be taken, however, if
| |
| − | interference patterns are created between the beams. As long as the
| |
| − | atoms move a distance greater than the wavelength, interference may be
| |
| − | neglected. But large field gradients can add extra forces and
| |
| − | heating.
| |
| − | | |
| − | One can also alternate between the six beams, but having simultaneous
| |
| − | beams actually turns out to be better, due to the interference between the beams. In particular, it gives polarization gradients
| |
| − | and other subtle effects which provide extra cooling. This wasn't initially forseen, but when implemented it was rapidly recognized that 3D cooling with six simultaneous beams was much more powerful than originally thought.
| |
| − | A significant landmark was achieved when, in 1985, Steve Chu used chirped slowing and a 3D molasses
| |
| − | configuration to obtain atoms colder than <math>1</math> mK, for the first time ([https://cua-admin.mit.edu:8443/wiki/images/4/47/Chu85_molasses.pdf Original paper on optical molasses, Chu et al.]).
| |
| − | | |
| − | === Cooling at high intensities ===
| |
| − | | |
| − | Let us consider an example, of laser cooling at high laser intensities. Keep in mind that laser cooling works because <math>F=-\alpha v</math> and
| |
| − | <math>\alpha>0</math>. Assume we have a detuning of about one linewith,
| |
| − | <math>\delta=-\Gamma</math>. Now plot the friction coefficient <math>\alpha</math> as a function of intensity:
| |
| − | | |
| − | ::[[Image:chapter1-intro-to-cooling-Lec1-high-inten.png|thumb|408px|none|]]
| |
| − | Initially, at small intensities, <math>\alpha</math> increases as a function of intensity. Don't be
| |
| − | confused by the fact that the Doppler limit is achieved at low
| |
| − | intensities. The diffusion coefficient is also linear in intensity at
| |
| − | low intensity. <math>\alpha</math> increases with <math>I/I_0</math> at first, and peaks
| |
| − | around <math>0.5</math>, but above the saturation limit <math>\alpha</math> actually changes
| |
| − | sign and starts heating. When <math>\alpha<0</math> then, counter-intuitively,
| |
| − | blue detuned light can be used to cool atoms.
| |
| | | | |
| − | ==== Cooling with blue detuned light ==== | + | == Magneto-Optical Traps == |
| | | | |
| − | This is a
| + | {{:Magneto-Optical Traps}} |
| − | non-trivial result (where does the energy go?), which we'll return to later, and understand in the
| |
| − | context of the optical Bloch equation and the dressed atom model (see [https://cua-admin.mit.edu:8443/wiki/images/a/af/Ashk83_Earnshaw.pdf Gordon and Ashkin]).
| |
| − | | |
| − | == Momentum and spatial diffusion ==
| |
| − | === Momentum diffusion ===
| |
| − | First, consider diffusion of the momentum of an atom being cooled.
| |
| − | The momentum diffusion coefficient is defined as
| |
| − | :<math>\begin{array}{rcl}
| |
| − | 2D^p = \frac{d}{dt} \langle (p- \langle p{\rangle}^2)^2{\rangle}
| |
| − | \,.
| |
| − | \end{array}</math>
| |
| − | This can be directly calculated if we have a fluctuating force, using
| |
| − | the fact that <math>d\vec{p}/dt = \vec{f}</math> is a force:
| |
| − | :<math>\begin{array}{rcl}
| |
| − | 2D^p &=& \frac{d}{dt} \left[
| |
| − | {\langle}\vec{p}\cdot\vec{p}{\rangle}-{\langle}\vec{p}{\rangle}{\langle}\vec{p} \rangle \right]
| |
| − | \\
| |
| − | &=& 2 \left[
| |
| − | {\langle}\vec{p}\cdot\vec{f}{\rangle}-{\langle}\vec{p}{\rangle}{\langle}\vec{f} \rangle \right]
| |
| − | \\ &=& 2 \int^0_{-\infty}
| |
| − | {\langle}\vec{f}(0) \cdot \vec{f}(t) \rangle - \langle \vec{f}(0) {\rangle}{\langle}
| |
| − | \vec{f}(t) \rangle \, dt
| |
| − | \,,
| |
| − | \end{array}</math>
| |
| − | showing that the diffusion is given by the integral of the force-force
| |
| − | correlation function. Essentially:
| |
| − | :<math>\begin{array}{rcl}
| |
| − | 2D^p
| |
| − | &=& 2 \int^0_{-\infty} \langle \vec{f}(t) \cdot \vec{f}(0) \rangle \, dt
| |
| − | \,.
| |
| − | \end{array}</math>
| |
| − | This results due to the fluctuation-dissipation theorem.
| |
| − | === Spatial diffusion ===
| |
| − | This is less frequently discussed in the literature compared with
| |
| − | momentum diffusion, but it is of practical importance in
| |
| − | experiments. Suppose the atoms start in a single point, embedded in a
| |
| − | 3D optical molasses. How does the point distribution expand? On the
| |
| − | time scale determined by <math>\alpha</math>, the atoms loose their memory of
| |
| − | their original velocities. The molasses has a nearly perfect thermal
| |
| − | distribution, despite atoms in the cloud never interacting with each
| |
| − | other, because they thermalize to the laser beam.
| |
| − | The damping time is
| |
| − | :<math>
| |
| − | \frac{1}{\gamma} = \frac{M}{\alpha}
| |
| − | \,.
| |
| − | </math>
| |
| − | Spatial diffusion can be described by a random walk (in space), with a
| |
| − | step size <math>L</math> given by the RMS velocity of the atoms and the damping
| |
| − | time,
| |
| − | :<math>
| |
| − | \ell = 2 \frac{v_{rms}}{\gamma}
| |
| − | \,,
| |
| − | </math>
| |
| − | where the extra factor of <math>2</math> comes from a more rigorous treatment.
| |
| − | Thus, starting from a point distribution, by the standard random walk
| |
| − | result, after time <math>t_d</math>, we obtain
| |
| − | :<math>
| |
| − | \langle r^2 \rangle = 2 \ell^2 t_d \gamma
| |
| − | \,,
| |
| − | </math>
| |
| − | where the number of steps is <math>t_d\gamma</math>. This is
| |
| − | :<math>\begin{array}{rcl}
| |
| − | \langle r^2 \rangle &=& 2 \frac{v_{rms}^2}{\gamma} t_d
| |
| − | \\
| |
| − | \frac{D^p t_d}{\alpha^2}
| |
| − | \,.
| |
| − | \end{array}</math>
| |
| − | Now recall the definition
| |
| − | :<math>
| |
| − | \langle r^2 \rangle = 2 D^x t_d
| |
| − | \,,
| |
| − | </math>
| |
| − | where <math>D^x</math> is the spatial diffusion coefficient.
| |
| − | This gives a relation between the spatial and momentum diffusion
| |
| − | coefficients,
| |
| − | :<math>
| |
| − | D^x = \frac{D^p}{\alpha^2} = \frac{KT}{\alpha}
| |
| − | \,.
| |
| − | </math>
| |
| − | Note the similarity of this expression with the Einstein relation for
| |
| − | carriers in semiconductors, <math>D/\mu = kT/q</math>.
| |
| − | These expressions are useful in the laboratory context, as an example
| |
| − | illustrates. How long does a typical trapped alkali atom (eg cesium
| |
| − | or sodium) take to diffuse out by <math>0.5</math> cm at the Doppler temperature?
| |
| − | Using the formulas above, we get <math>t_d = 1</math> second. This is very
| |
| − | accessible in the laboratory, and is one of the reasons why optical
| |
| − | molasses are so useful in practice.
| |
| | | | |
| | == References == | | == References == |
| | | | |
| | [[Category:Light forces]] | | [[Category:Light forces]] |
| | + | |
| | + | * References: |
| | + | ** Molasses, beam slowing and MOT: |
| | + | ** Nice summary on both dipole traps and radiation pressure traps |
| | + | *** W.D. Phillips, Laser cooling and trapping of neutral atoms, in Laser Manipulation of Atoms and Ions, edited by E. Arimondo, W.D. Phillips, and F. Strumia, Proceedings of the International School of Physics “Enrico Fermi”, Course CXVIII (North-Holland, Amsterdam, 1992) [http://cua.mit.edu/8.422%5FS07/phil92_varenna.pdf Download] |
| | + | ** [https://cua-admin.mit.edu:8443/wiki/images/4/47/Chu85_molasses.pdf Original paper on optical molasses, Chu et al.] |
| | + | ** [https://cua-admin.mit.edu:8443/wiki/images/f/f7/Raab87_MOT.pdf Original paper on MOT, Raab et al.] |
| | + | ** Original papers on optical Earnshaw theorem |
| | + | *** [https://cua-admin.mit.edu:8443/wiki/images/a/af/Ashk83_Earnshaw.pdf Ashkin and Gordon] |
| | + | *** [https://cua-admin.mit.edu:8443/wiki/images/e/ec/Prit86_spont_force_traps.pdf Pritchard et al.] |
Spontaneous emission leads to a redistribution of momentum of an atom, absorbed from incident photons. Here, we discuss three applications of this spontaneous light force:
- Optical Molasses
- Beam Slowing
- Magneto-Optical Traps
Optical Molasses
An optical molasses is formed by laser cooling of atoms using the spontaneous light force. We study this first by reviewing the spontaneous light force, then investigating a one-dimensional molasses. This provides an excellent scenario to establish an important limit to laser cooling, the Doppler limit, beyond which laser Doppler cooling fails due to the balance established between momentum loss and diffusion of momentum due to the randomness of the classical light field. We then describe the three-dimensional molasses, and conclude with a discussion of laser cooling as an illustration of the fluctuation-dissipation theorem of statistical physics.
The spontaneous light force
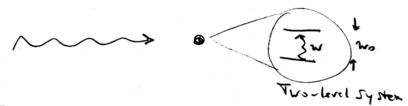
Consider a two-level atom with energy spacing  ,
interacting with a single mode laser beam:
,
interacting with a single mode laser beam:
Let the laser intensity be  , and the interaction matrix element
between atom and light be
, and the interaction matrix element
between atom and light be  , where
, where  is known as the Rabi frequency,
is known as the Rabi frequency,
 is the electric field strength, and
is the electric field strength, and  is the dipole
moment of the atom.
is the dipole
moment of the atom.
It is useful to define a quantity known as the saturation intensity
 as the intensity of light at which the rabi frequency becomes
as the intensity of light at which the rabi frequency becomes
 , where
, where  is the spontaneous
emission rate (the natural decay rate of the atom from
is the spontaneous
emission rate (the natural decay rate of the atom from  to
to
 , excited to ground state). This gives
, excited to ground state). This gives

The rate at which photons are scattered from the atom is known to be

where  is the frequency detuning of the laser from the center
of resonance of the atom. Two useful limits of this scattering rate
are
is the frequency detuning of the laser from the center
of resonance of the atom. Two useful limits of this scattering rate
are

where we have assumed  (resonant light). These expressions
have a natural physical interpretation: in the limit of infinite
intensity, the atomic levels become equally populated between the
excited and ground state, and thus only half the atoms (the excited
ones) can scatter light. Thus, the scattering rate is
(resonant light). These expressions
have a natural physical interpretation: in the limit of infinite
intensity, the atomic levels become equally populated between the
excited and ground state, and thus only half the atoms (the excited
ones) can scatter light. Thus, the scattering rate is  in
that limit.
in
that limit.
Suppose the force imparted by light on the atom is given by the recoil
of photons spontaneously emitted from the atom. This force would then
be

where  is the momentum of each photon. This expression makes
several assumptions: that is is the net momentum transfer in absorption,
that there is no "stimulated" force, and that
is the momentum of each photon. This expression makes
several assumptions: that is is the net momentum transfer in absorption,
that there is no "stimulated" force, and that  , meaning that the jump in the Doppler shift is less than the
natural linewidth.
, meaning that the jump in the Doppler shift is less than the
natural linewidth.
Typically, for alkali atoms, this force is  times the
mass of an atom (
times the
mass of an atom ( being the acceleration due to gravity). This
means that light can stop a sodium atom going at
being the acceleration due to gravity). This
means that light can stop a sodium atom going at  m/s in one
millisecond, or about half a meter. In comparison to electrostatic
forces on ions, this is very small, however: it is comparable to the
force exerted by an electric field of 1 millivolt/cm on an ionized
sodium atom.
m/s in one
millisecond, or about half a meter. In comparison to electrostatic
forces on ions, this is very small, however: it is comparable to the
force exerted by an electric field of 1 millivolt/cm on an ionized
sodium atom.
Moving atoms experience a Doppler shift, which we can model as a
frequency dependent force, based on Eq.(\ref{eq:ci:lorentzian}), as
![{\displaystyle F=\hbar k{\frac {\Gamma }{2}}{\frac {I/I_{0}}{1+{\frac {I}{I_{0}}}+\left[{\frac {2(\delta +kv)}{\Gamma }}\right]^{2}}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e53b4cc1667f30f60210a324981e8cfef1d320c6)
where  is the velocity of the atom. The effect of a fixed laser
frequency on an ensemble of atoms is to modify their Maxwell-Boltzmann
thermal velocity distribution:
is the velocity of the atom. The effect of a fixed laser
frequency on an ensemble of atoms is to modify their Maxwell-Boltzmann
thermal velocity distribution:
Note how the initial distribution changes to one with atoms piling up
below the velocity group resonant with the laser. The atoms bunch.
Historically, this is the first method that was done to cool atoms to
Kelvin temperatures.
One-dimensional optical molasses
Let us now turn to a method which allows cooling of atoms to zero
velocity. Consider two laser beams incident on an atom from opposite
directions. We assume that the total force is the sum of the two
forces, ignore standing wave effects, and take the laser intensity to
be low compared with the saturation intensity,  . Taking the
force to be the sum of two forces described by Eq.(\ref{eq:ci:vdf}),
we find that the two lorentzians sum to give the following force as a
function of velocity:
. Taking the
force to be the sum of two forces described by Eq.(\ref{eq:ci:vdf}),
we find that the two lorentzians sum to give the following force as a
function of velocity:
The velocity dependent force is positive from one light beam, and
negative from the other. With a detuning chosen such that force is
zero at zero velocity, the force around  can be expanded
linearly, giving
can be expanded
linearly, giving

where  describes the viscosity imparted by the light
force to the atom, reflecting the restoring force applied when the
atom is not at zero velocity. This configuration is known as an
optical molasses, because of this restoring force, which makes the
light behave like a thick, viscous medium for the atoms in it.
The damping coefficient
describes the viscosity imparted by the light
force to the atom, reflecting the restoring force applied when the
atom is not at zero velocity. This configuration is known as an
optical molasses, because of this restoring force, which makes the
light behave like a thick, viscous medium for the atoms in it.
The damping coefficient  can be calculated to be
can be calculated to be

The Doppler cooling limit
We have seen that the spontaneous light force, characterized by the
Lorentzian response of an atom to light, together with the Doppler
shift due to movement of the atom, gives a velocity dependent force,
which can be zero at zero velocity. Does this mean that the atoms can
be cooled to zero temperature?
If the rate of energy loss due to cooling is

then we should reach zero velocity, and zero temperature. Indeed, the
kinetic energy decays exponentially. However, the spontaneous force
has a random character, and thus has fluctuations which limit the
minimum temperature achievable.
Momentum diffusion limit
This limit is determined by momentum diffusion. The force imparted
can be described by a random walk. The final momentum is

on average, due to the random walk. Note that the momentum spread is

This describes heating which arises due to photons randomly scattering
in all directions, such that the net momentum almost adds up to zero,
but not quite. There is also a similar term due to absorption: some
atoms will absorb more or fewer photons, due to the Poissonian
statistics of absorption.
Time variation of kinetic energy
The time variation of the kinetic energy due to the spontaneous emission is
forces is

where  is the momentum diffusion coefficient
is the momentum diffusion coefficient

And  is
is  in the special case that we only
consider the heating due to spontaneous emission. Later we'll see that
in the special case that we only
consider the heating due to spontaneous emission. Later we'll see that  is a correlation function of the force fluctuations.
is a correlation function of the force fluctuations.
Accounting for the Poissonian variance in number of absorbed photons
adds a factor of two to the heating rate, which yields

Balance of heating and cooling
Let us now derive the Doppler limit for cooling. In equilibrium,
 . This means
. This means

The heating rate is independent of kinetic energy, whereas the cooling
rate is a function of kinetic energy. So as the atoms cool down, the
cooling rate slows down, resulting in a final temperature equilibrium
being reached:

 is a viscosity parameter: it reflects transport.
is a viscosity parameter: it reflects transport.  reflects mobility. Thus, this is an Einstein relation, a universal
expression in statistical mechanics resulting from the fundamental
theorem which relates dissipation to fluctuations.
reflects mobility. Thus, this is an Einstein relation, a universal
expression in statistical mechanics resulting from the fundamental
theorem which relates dissipation to fluctuations.
The Doppler limit temperature
We've now obtained an expression for the Doppler limit temperature, a
limit on the temperature an ideal two-level atom can be cooled to by
laser beams,

This optimal temperature is achieved for  , and detuning of
, and detuning of
 (half a linewidth). Physically, at low
temperatures, the atom cannot determine whether the photon comes from
left or right; at higher temperatures, the atom can discriminate
whether photons come from left or right, thus cooling. For sodium,
this temperature is
(half a linewidth). Physically, at low
temperatures, the atom cannot determine whether the photon comes from
left or right; at higher temperatures, the atom can discriminate
whether photons come from left or right, thus cooling. For sodium,
this temperature is 
 K, corresponding to a velocity of
K, corresponding to a velocity of  cm/s.
cm/s.
3D molasses, high intensities
To cool atoms along not just one axis, but along three axes, use six
counter-propagating laser beams. This configuration is called a 3D
molasses. Everything we've discussed in one dimension can be applied;
just sum up the forces. Some care must be taken, however, if
interference patterns are created between the beams. As long as the
atoms move a distance greater than the wavelength, interference may be
neglected. But large field gradients can add extra forces and
heating.
One can also alternate between the six beams, but having simultaneous
beams actually turns out to be better, due to the interference between the beams. In particular, it gives polarization gradients
and other subtle effects which provide extra cooling. This wasn't initially forseen, but when implemented it was rapidly recognized that 3D cooling with six simultaneous beams was much more powerful than originally thought.
A significant landmark was achieved when, in 1985, Steve Chu used chirped slowing and a 3D molasses
configuration to obtain atoms colder than  mK, for the first time (Original paper on optical molasses, Chu et al.).
mK, for the first time (Original paper on optical molasses, Chu et al.).
Cooling at high intensities
Let us consider an example, of laser cooling at high laser intensities. Keep in mind that laser cooling works because  and
and
 . Assume we have a detuning of about one linewith,
. Assume we have a detuning of about one linewith,
 . Now plot the friction coefficient
. Now plot the friction coefficient  as a function of intensity:
as a function of intensity:
Initially, at small intensities,  increases as a function of intensity. Don't be
confused by the fact that the Doppler limit is achieved at low
intensities. The diffusion coefficient is also linear in intensity at
low intensity.
increases as a function of intensity. Don't be
confused by the fact that the Doppler limit is achieved at low
intensities. The diffusion coefficient is also linear in intensity at
low intensity.  increases with
increases with  at first, and peaks
around
at first, and peaks
around  , but above the saturation limit
, but above the saturation limit  actually changes
sign and starts heating. When
actually changes
sign and starts heating. When  then, counter-intuitively,
blue detuned light can be used to cool atoms.
then, counter-intuitively,
blue detuned light can be used to cool atoms.
Cooling with blue detuned light
This is a
non-trivial result (where does the energy go?), which can be undersood in the
context of the optical Bloch equation and the dressed atom model (see Gordon and Ashkin).
Specifically, the underlying physical reason which allows blue detuned light to cool is that
at low intensities, the force seen by an atom comes from adding two
Lorentzians, as we have seen; this fails at higher intensities, however.
In particular, the optical Bloch equation component  combines with the usual steady state term a new a
velocity dependent term:
combines with the usual steady state term a new a
velocity dependent term:

One can approximate that  When you average the light force in the standing wave over an optical
wavelength, then you find an average force which is a friction force,
When you average the light force in the standing wave over an optical
wavelength, then you find an average force which is a friction force,

At weak intensities,  , but at high
intensities
, but at high
intensities  changes sign.
changes sign.
Momentum and spatial diffusion
Let us return to the physics of the randomness of spontaneous light force induced cooling, and revisit the behavior of the diffusion of the cooled atom's momentum and spatial position. We shall see that the physical balance involved is an excellent example of the important fluctuation-dissipation theorem of statistical mechanics.
Momentum diffusion
First, consider diffusion of the momentum of an atom being cooled.
The momentum diffusion coefficient is defined as

This can be directly calculated if we have a fluctuating force, using
the fact that  is a force:
is a force:
![{\displaystyle {\begin{array}{rcl}2D^{p}&=&{\frac {d}{dt}}\left[{\langle }{\vec {p}}\cdot {\vec {p}}{\rangle }-{\langle }{\vec {p}}{\rangle }{\langle }{\vec {p}}\rangle \right]\\&=&2\left[{\langle }{\vec {p}}\cdot {\vec {f}}{\rangle }-{\langle }{\vec {p}}{\rangle }{\langle }{\vec {f}}\rangle \right]\\&=&2\int _{-\infty }^{0}{\langle }{\vec {f}}(0)\cdot {\vec {f}}(t)\rangle -\langle {\vec {f}}(0){\rangle }{\langle }{\vec {f}}(t)\rangle \,dt\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02a7ffc7ff5cebc8f7bb85ff2b1089df0841cb45)
showing that the diffusion is given by the integral of the force-force
correlation function. Essentially:

This results due to the fluctuation-dissipation theorem.
Spatial diffusion
Spatial diffusion is less frequently discussed in the literature compared with
momentum diffusion, but it is of practical importance in
experiments. Suppose the atoms start in a single point, embedded in a
3D optical molasses. How does the point distribution expand? On the
time scale determined by  , the atoms loose their memory of
their original velocities. The molasses has a nearly perfect thermal
distribution, despite atoms in the cloud never interacting with each
other, because they thermalize to the laser beam.
, the atoms loose their memory of
their original velocities. The molasses has a nearly perfect thermal
distribution, despite atoms in the cloud never interacting with each
other, because they thermalize to the laser beam.
The damping time is

Spatial diffusion can be described by a random walk (in space), with a
step size  given by the RMS velocity of the atoms and the damping
time,
given by the RMS velocity of the atoms and the damping
time,

Thus, starting from a point distribution, by the standard random walk
result, after time  , we obtain
, we obtain

where the number of steps is  and the extra factor of
and the extra factor of  comes from a more rigorous treatment.. This is
comes from a more rigorous treatment.. This is

Now recall the definition

where  is the spatial diffusion coefficient.
This gives a relation between the spatial and momentum diffusion
coefficients,
is the spatial diffusion coefficient.
This gives a relation between the spatial and momentum diffusion
coefficients,

Note the similarity of this expression with the Einstein relation for
carriers in semiconductors,  .
.
Example: laser cooling of sodium atoms
These expressions are useful in the laboratory context, as an example
illustrates. How long does a typical trapped alkali atom (eg cesium
or sodium) take to diffuse out by  cm at the Doppler temperature?
Using the formulas above, we get
cm at the Doppler temperature?
Using the formulas above, we get  second. This is very
accessible in the laboratory, and is one of the reasons why optical
molasses are so useful in practice.
second. This is very
accessible in the laboratory, and is one of the reasons why optical
molasses are so useful in practice.
Beam slowing
We have previously looked at cooling with two laser beams, focusing on
the idea that if you want to cool, you need a force which is linear
with velocity. Now, let us see how you can cool with a single laser
beam. That is what you do when you have a single atomic beam. With a
single laser beam, you can not only slow them down, but also bunch
them up, obtaining the same velocity distribution you get with a
molasses. This is the only example of laser cooling I know of which
has a very simple, closed form solution, which is possible because
there is only one laser beam.
Imagine, if you have a single Lorentzian, how can you cool?
Generically, you need a "lock" point, which is stable and has atoms
moving to that point in phase space from either velocity direction.
With a single beam you don't apparently have such, but as we shall see
there is something else interesting that can be done.
Consider a single beam of atoms, with this velocity distribution.
Using a laser, you can push some of the atoms to become cooler (red
line below), bunching them up in a lower velocity regime, and leaving
atoms faster than some velocity unchanged. What do you have to do if
you want to bunch all the atoms at zero velocity? It becomes clear
that you want more than one laser frequency, for example. By applying
a broad range of frequencies which cover the whole velocity
distribution, you can slow down all the atoms. There are several
techniques using such an approach, known as white light slowing, or
diffuse light slowing. But none of those are as powerful as
{\em chirped slowing} and {\em Zeeman slowing}, the techniques of choice
in modern laser cooling.
Chirped slowing
The idea behind chirped slowing is to get the atoms to "ride the surf". In other words, the frequency chirp of the laser beam and the deceleration of the atoms should be synchronized.
Balance of equations
Step 1
The force on an atom in the beam due to the light is
![{\displaystyle F=-\hbar k{\frac {\Gamma }{2}}{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta +kv)}{\Gamma }}\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dfb969d3cde2f98dcdf4cf800b63c3543426809)
Let  denote the atom's acceleration.
Let us assume a frame of reference and experimental setup such that
denote the atom's acceleration.
Let us assume a frame of reference and experimental setup such that
 ,
,  ,
,  ,
,  . We can call
. We can call  , where
, where  is the atom's mass.
is the atom's mass.
Step 2
The scheme begins by selecting the deceleration desired, some  .
Then set
.
Then set  , and look for a
, and look for a  to obtain
this desired force.
This will exist if
to obtain
this desired force.
This will exist if

Step 3
Next, select an initial velocity  such that
such that  .
.
 is the detuning for this "targeted" velocity group, so we
must provide a laser with frequency in the lab frame of
is the detuning for this "targeted" velocity group, so we
must provide a laser with frequency in the lab frame of  . The atom's velocity will differ from the desired
target group by
. The atom's velocity will differ from the desired
target group by  .
.
Step 4
With these definitions, we now have
![{\displaystyle F=-\hbar k{\frac {\Gamma }{2}}{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta '+kv')}{\Gamma }}\right]^{2}}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087622d4991f57f7abd12a596702081e4efe6480)
in the frame of reference of the atoms in the target velocity group.
Step 5
Transforming into this decelerating frame, we get a fictitious force
with is  , and
, and
![{\displaystyle F'(v')=Ma_{max}\left[{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta '+kv')}{\Gamma }}\right]^{2}}}+{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta ')}{\Gamma }}\right]^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0772bab6a738e2ee29b5c0ea76102175dfe6e28)
This second term has the same structure as the first, but it is
velocity independent. Note that this is exact, and valid for arbitrary  . All we've done is to substitute definitions, so far, but they provide useful intuition.
. All we've done is to substitute definitions, so far, but they provide useful intuition.
Note that for small  , this force is linear in velocity,
, this force is linear in velocity,  .
.
Decelerating Frame
In the lab frame, we have a force which is a positive Lorentzian. In
the decelerating frame, we had to add  (the inertial force),
so this Lorentzian shifts down, when we plot the total force as a function of the velocity in the decelerating frame
(the inertial force),
so this Lorentzian shifts down, when we plot the total force as a function of the velocity in the decelerating frame  :
:
Therefore, there is now a stable "lock" point, where  as a
function of
as a
function of  . In other words, when the atoms have a negative velocity
. In other words, when the atoms have a negative velocity  , the atoms all accelerate towards zero velocity (in the decelerating frame). And when atoms have a small positive velocity, they also move towards
, the atoms all accelerate towards zero velocity (in the decelerating frame). And when atoms have a small positive velocity, they also move towards  . In contrast the point where the Lorentzian has
. In contrast the point where the Lorentzian has  at
at  , is unstable.
, is unstable.
Thus, we may write, as we did with the molasses, an
expression for the linearized force around this point,  , in which
, in which  . There is also randomness, as there was in the optical molasses case, for which we may calculate a momentum diffusion
coefficient, and we find that
. There is also randomness, as there was in the optical molasses case, for which we may calculate a momentum diffusion
coefficient, and we find that  . Thus,
the final temperature limit of the beam is actually the same as that
achievable with a molasses:
. Thus,
the final temperature limit of the beam is actually the same as that
achievable with a molasses:  .
.
We've seen that one laser can bunch up atoms from a beam at a single
velocity. Physically, what happens is that if the atoms fall behind,
the light does not interact with them, but if the atoms are too fast,
the laser cools them, much like in the molasses case.
Graphical summary
Here is a graphical summary of what we've learned about beam slowing.
In the decelerating frame, this is the situation. Change sign, so
that in the frame the decelerating force is positive, for this graph:
Initially, our zero force point is at the targeted velocity  .
All atoms at larger velocity experience a constant positive force,
accelerating them. After a later time
.
All atoms at larger velocity experience a constant positive force,
accelerating them. After a later time  , the tail of the
maxwell-Boltzmann distribution is pushed to higher velocities. The peak of distribution of atoms grows higher and higher with time, while the positive tail moves to higher velocities.
, the tail of the
maxwell-Boltzmann distribution is pushed to higher velocities. The peak of distribution of atoms grows higher and higher with time, while the positive tail moves to higher velocities.
This is the description in the decelerating frame.
In the lab frame, we shift from  back to
back to  . This means that we just shift all the distributions down in velocity. We start with a broad distribution at
. This means that we just shift all the distributions down in velocity. We start with a broad distribution at  . There is a velocity group at
. There is a velocity group at  which is on resonance with the laser beam. As time goes on, the laser beam chirps, causing more and more atoms to come into resonance, piling them up in a lower velocity class. What happens is that after the laser beam is switched off, you may still have a low velocity tail which is not reached by the laser, but you have a huge peak of atoms that have been cooled:
which is on resonance with the laser beam. As time goes on, the laser beam chirps, causing more and more atoms to come into resonance, piling them up in a lower velocity class. What happens is that after the laser beam is switched off, you may still have a low velocity tail which is not reached by the laser, but you have a huge peak of atoms that have been cooled:
All the atoms at lower velocities are pushed up in velocity
until they stack up at  , producing a narrow distribution around
, producing a narrow distribution around
 .
.
The width of this narrow velocity distribution is given by  , which is proportional to
, which is proportional to
 .
.
Beam cooling is actually the simplest and cleanest example of laser
cooling. It has the same physics as the molasses case, with the second beam being replaced in a sense by a ficticious force. Note that in the two-beam molasses case, there are more complications, since one should really
consider interference effects.
Energy conservation in laser cooling
Kinetic energy conservation
Where does the lost kinetic energy go, in cooling the atoms? In the beam cooling scenario, for example, you have moved a large number of atoms from high velocities to low velocities. How can this be reconciled with energy conservation? Well, there are only several possibilities for where the energy can go. In particular, there is light scattered by the atoms, and the energy is radiated away by spontaneous emission, as we shall now see.
Absorption is responsible for momentum change, and emission is responsible for energy conservation. Light emitted by the atom is at the resonant energy  , but
can be absorbed when the photon is just slightly less than
, but
can be absorbed when the photon is just slightly less than  .
The emission is isotropic, whereas the incident light is directed and
Doppler shift dependent.
.
The emission is isotropic, whereas the incident light is directed and
Doppler shift dependent.
Doppler cooling can be explained in this picture. Incident laser light is
detuned below  ("red detuned"), whereas emitted photons are, on average, at a higher frequency, so more energy is emitted than is absorbed, when an atom is cooled.
("red detuned"), whereas emitted photons are, on average, at a higher frequency, so more energy is emitted than is absorbed, when an atom is cooled.
Energy conservation in general cooling schemes
The same intuition can be applied to all cooling schemes, including those used to cool solids and liquids. Phonon
assisted absorption is balanced against emission, resulting in cooling:
How hard is it to cool liquids and solids? Consider a system at
 K; that gives the phonon energy. Then
K; that gives the phonon energy. Then  Kelvin. In practice, there is a lower than unity fluorescence quantum
yield, because there are non-radiative ways to exit the excited
state. The cooling will be efficient, however, only when the quantum
yield is higher than
Kelvin. In practice, there is a lower than unity fluorescence quantum
yield, because there are non-radiative ways to exit the excited
state. The cooling will be efficient, however, only when the quantum
yield is higher than  , which is typically unrealistic.
Cooling with laser light is therefore not typically practical, for
systems other than atoms, which have a unity fluorescence quantum
yield. Molecules are hard, because they have non-radiative
de-excitation pathways.
, which is typically unrealistic.
Cooling with laser light is therefore not typically practical, for
systems other than atoms, which have a unity fluorescence quantum
yield. Molecules are hard, because they have non-radiative
de-excitation pathways.
Magneto-Optical Traps
The Magneto-Optical Trap (MOT) is a configuration of atoms in laser
cooling beams and coils producing static magnetic fields, which is
astonishingly effective in cooling atoms from room temperature to
microkelvin scale temperatures. Today, the MOT is a workhorse of
atomic physics, and the starting point for many atomic physics
experiments, such as with Bose-Einstein condensates.
We begin our study of the MOT with an explanation of how it was
originally thought to be impossible, due to the optical Earnshaw
theorem. We then present the physics of two-level atoms in a
one-dimensional MOT, from which generalization to 3D MOT's trapping
real multi-level atoms is straightforward.
Optical Earnshaw Theorem
Some history helps place the MOT in context. In the 1970's and
1980's, many people discussed prospects for, and limitations of the
stimulated and spontaneous force. In 1983, Gordon and Ashkin derived
the optical Earnshaw theorem. The (standard, electromagnetic)
Earnshaw theorem states that a charged particle will never be in a
stable equilibrium in a static, 3D configuration of electric fields.
This holds because for a particle to be stable, all field lines must
point inwards, but we know that the divergence of the electric field
in vacuum is zero.
The optical Earnshaw theorem states, in a similar way, that a 3D
sponteneous light force trap is not possible. This was not a very
positive start for atom trapping. The proof goes as follows. Recall
that the sponeaneous light force is related to the Poynting vector as

where  is the Poynting vector. From electromagnetism,
however, we know that
is the Poynting vector. From electromagnetism,
however, we know that

but we know that  if there is zero
local energy density
if there is zero
local energy density  . This contradicts the requirement that
. This contradicts the requirement that
 .
.
Where is the flaw in this reasoning? In 1986, David Pritchard
realized there were many ways to circumvent the optical Earnshaw
theorem. What is ignored here is the {\em internal structure of the
atom}. After all, the spontaneous light force is actually not just
proportional to the incident light flux. The assumption that every
atom which is exposed to the same Poynting vector experiences the same
force, is just wrong. Namely,

The force can thus be spatially dependent. First,  can
experience saturation. Second, optical pumping can be used, taking
advantage of internal structure of the atoms. Third, there can be
line shifts due to external static fields, as when hyperfine states
are used which are magnetic field sensitive.
can
experience saturation. Second, optical pumping can be used, taking
advantage of internal structure of the atoms. Third, there can be
line shifts due to external static fields, as when hyperfine states
are used which are magnetic field sensitive.
The perfect solution was demonstrated in 1987, in a collaboration
between MIT (paper by Raab et al) and Steve Chu's group at Bell Labs.
1-dimensional MOT
Consider two counterpropagating laser beams with opposite circular
polarizations, incident on some atoms, in the presence of a static
magnetic field gradient:
The energy levels of three hyperfine levels, with  and
and  ,
become a function of space due to the magnetic field, so that the
,
become a function of space due to the magnetic field, so that the
 and
and  polarized light beams interact with
spatially localized classes of atoms:
polarized light beams interact with
spatially localized classes of atoms:
This scenario is similar to an optical molasses, but the frequency
shifts  are due to a magnetic field gradient
are due to a magnetic field gradient  . Just as in the molasses analysis, we must add the effects
of the left and right laser beams. Assume we have low intensity, so
we find that
. Just as in the molasses analysis, we must add the effects
of the left and right laser beams. Assume we have low intensity, so
we find that
![{\displaystyle F=F_{R}+F_{L}={\frac {\hbar k\Gamma }{2}}\left[{\frac {I/I_{0}}{1+4\left({\frac {\delta -kv-\beta z}{\Gamma }}\right)^{2}}}-\cdots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e91be23117a1f715e22d380a3bac9491e5be4f4)
For small  ,
,  ,
,
![{\displaystyle F(v,z)={\frac {\hbar k\Gamma }{2}}\left[-kv-\beta z\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf931fc215e9c18a397895ee24334ac6d33b5792)
The equation of motion for the atom is thus that of a harmonic
oscillator, because the force is linear with displacement:

where the trap frequency is given by the ratio of the light momentum
 and the field gradient strenght
and the field gradient strenght  ,
,

Typically, experimental parameters lead this to be an overdamped
harmonic oscillator, with  kHz,
and a damping time of about
kHz,
and a damping time of about 
 s. The static well depth is
usually around a few Kelvin, but the dynamic depth is even larger.
The dynamic depth refers to how much kinetic energy an atom can get
before it is recaptured by the trap, because it is cooled by optical
molasses effects even after it leaves the local potential well.
s. The static well depth is
usually around a few Kelvin, but the dynamic depth is even larger.
The dynamic depth refers to how much kinetic energy an atom can get
before it is recaptured by the trap, because it is cooled by optical
molasses effects even after it leaves the local potential well.
3D MOT trapping with real atoms
Real atoms have a multilevel structure, with complicated hyperfine
structure. If you have a complicated ground state structure, you need
to include optical pumping effects between all the levels, but the
combination of these effects and the simple Zeeman shift model
discussed above works very well.
Recall that optical molasses works better than originally anticipated,
in which it was found that the damping due to polarization gradients
was much much larger than the damping due to doppler cooling,
 The same turns out to be true
for the restoring force in magneto-optical traps.
The same turns out to be true
for the restoring force in magneto-optical traps.
We have discussed only the 1D scheme above. You may not appreciate
it, but a lot of spontaneous light forces which were discussed to
circumvent the optical Earnshaw theorem worked in 1D, but were very
difficult to generalize to 3D. The MOT scheme, on the other hand,
generalizes very well to 3D. By using three pairs of anti-Helmholtz
coils to create the field gradients, and six laser beams, you get the
generalizeation to 3D and it works as well as in one dimension.
Example: vapor cell MOT
Consider a cesium vapor cell MOT. The atoms, initially at 300K, can
be cooled to 
 K. The density starts at
K. The density starts at  cm
cm ,
which is increased to
,
which is increased to  cm
cm . This means that the phase
space density, which is
. This means that the phase
space density, which is  , has been increased by
, has been increased by  order
of magnitude. Initially, the phase space density before cooling is
order
of magnitude. Initially, the phase space density before cooling is
 orders magnitide away from Bose-Einstein condensation; after MOT
trapping, the system is much closer - only
orders magnitide away from Bose-Einstein condensation; after MOT
trapping, the system is much closer - only  orders of magnitude
closer, but not yet there.
orders of magnitude
closer, but not yet there.
References
- References:
- Molasses, beam slowing and MOT:
- Nice summary on both dipole traps and radiation pressure traps
- W.D. Phillips, Laser cooling and trapping of neutral atoms, in Laser Manipulation of Atoms and Ions, edited by E. Arimondo, W.D. Phillips, and F. Strumia, Proceedings of the International School of Physics “Enrico Fermi”, Course CXVIII (North-Holland, Amsterdam, 1992) Download
- Original paper on optical molasses, Chu et al.
- Original paper on MOT, Raab et al.
- Original papers on optical Earnshaw theorem























![{\displaystyle F=\hbar k{\frac {\Gamma }{2}}{\frac {I/I_{0}}{1+{\frac {I}{I_{0}}}+\left[{\frac {2(\delta +kv)}{\Gamma }}\right]^{2}}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e53b4cc1667f30f60210a324981e8cfef1d320c6)

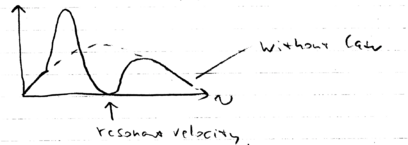

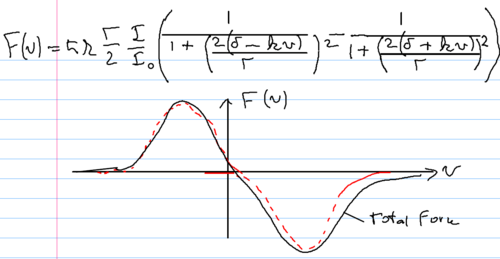
























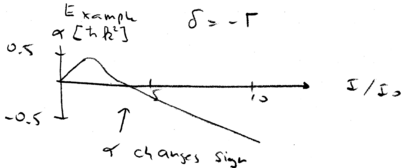










![{\displaystyle {\begin{array}{rcl}2D^{p}&=&{\frac {d}{dt}}\left[{\langle }{\vec {p}}\cdot {\vec {p}}{\rangle }-{\langle }{\vec {p}}{\rangle }{\langle }{\vec {p}}\rangle \right]\\&=&2\left[{\langle }{\vec {p}}\cdot {\vec {f}}{\rangle }-{\langle }{\vec {p}}{\rangle }{\langle }{\vec {f}}\rangle \right]\\&=&2\int _{-\infty }^{0}{\langle }{\vec {f}}(0)\cdot {\vec {f}}(t)\rangle -\langle {\vec {f}}(0){\rangle }{\langle }{\vec {f}}(t)\rangle \,dt\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02a7ffc7ff5cebc8f7bb85ff2b1089df0841cb45)














![{\displaystyle F=-\hbar k{\frac {\Gamma }{2}}{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta +kv)}{\Gamma }}\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dfb969d3cde2f98dcdf4cf800b63c3543426809)















![{\displaystyle F=-\hbar k{\frac {\Gamma }{2}}{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta '+kv')}{\Gamma }}\right]^{2}}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087622d4991f57f7abd12a596702081e4efe6480)

![{\displaystyle F'(v')=Ma_{max}\left[{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta '+kv')}{\Gamma }}\right]^{2}}}+{\frac {I/I_{0}}{1+I/I_{0}+\left[{\frac {2(\delta ')}{\Gamma }}\right]^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0772bab6a738e2ee29b5c0ea76102175dfe6e28)



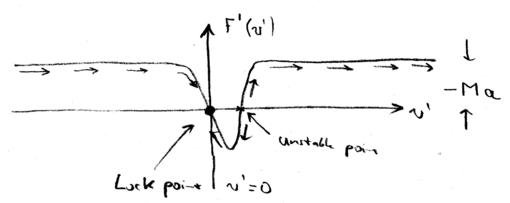







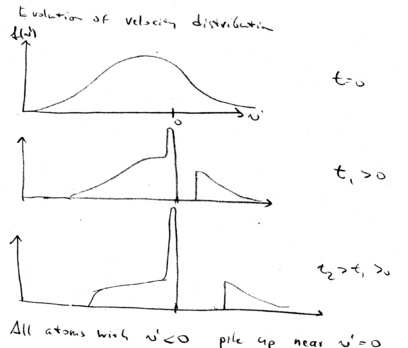


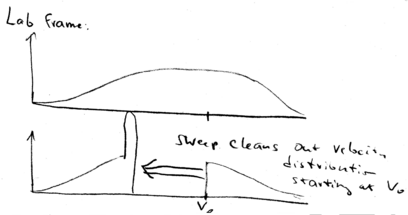


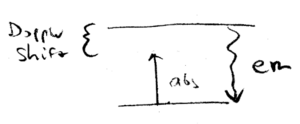
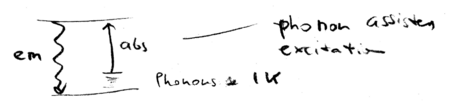











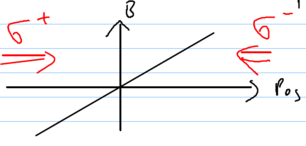




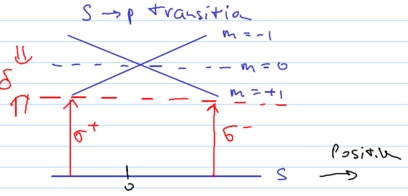


![{\displaystyle F=F_{R}+F_{L}={\frac {\hbar k\Gamma }{2}}\left[{\frac {I/I_{0}}{1+4\left({\frac {\delta -kv-\beta z}{\Gamma }}\right)^{2}}}-\cdots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e91be23117a1f715e22d380a3bac9491e5be4f4)

![{\displaystyle F(v,z)={\frac {\hbar k\Gamma }{2}}\left[-kv-\beta z\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf931fc215e9c18a397895ee24334ac6d33b5792)















